Kinematic analysis of shallow tunnel in layered strata considering joined effects of settlement and seepage
来源期刊:中南大学学报(英文版)2018年第2期
论文作者:鲁四平 张睿
文章页码:368 - 378
Key words:collapse mechanism; layered rocks; Hoek-Brown criterion; seepage force; surface settlement
Abstract: The purpose of this work is to predict the state of collapse in shallow tunnel in layered strata by using a new curved failure mechanism within the framework of upper bound theorem. Particular emphasis is first given to consider the effects of seepage forces and surface settlement. Furthermore, the Hoek-Brown nonlinear failure criterion is adopted to analyze the influence of different factors on the collapsing shape. Two different curve functions which describe two different rock layers are obtained by virtual work equations under the variational principle. According to the numerical results, the parameter B in Hoek-Brown failure criterion and the unit weights in different rock layers have a positive relationship with the size of collapsing block while pore pressure coefficient and the parameter A in Hoek-Brown failure criterion present a reverse tend.
Cite this article as: ZHANG Rui, LU Si-ping. Kinematic analysis of shallow tunnel in layered strata considering joined effects of settlement and seepage [J]. Journal of Central South University, 2018, 25(2): 368–378. DOI: https://doi.org/ 10.1007/s11771-018-3743-6.

J. Cent. South Univ. (2018) 25: 368-378
DOI: https://doi.org/10.1007/s11771-018-3743-6
ZHANG Rui(张睿), LU Si-ping(鲁四平)
School of Civil Engineering, Central South University, Changsha 410075, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Abstract: The purpose of this work is to predict the state of collapse in shallow tunnel in layered strata by using a new curved failure mechanism within the framework of upper bound theorem. Particular emphasis is first given to consider the effects of seepage forces and surface settlement. Furthermore, the Hoek-Brown nonlinear failure criterion is adopted to analyze the influence of different factors on the collapsing shape. Two different curve functions which describe two different rock layers are obtained by virtual work equations under the variational principle. According to the numerical results, the parameter B in Hoek-Brown failure criterion and the unit weights in different rock layers have a positive relationship with the size of collapsing block while pore pressure coefficient and the parameter A in Hoek-Brown failure criterion present a reverse tend.
Key words: collapse mechanism; layered rocks; Hoek-Brown criterion; seepage force; surface settlement
Cite this article as: ZHANG Rui, LU Si-ping. Kinematic analysis of shallow tunnel in layered strata considering joined effects of settlement and seepage [J]. Journal of Central South University, 2018, 25(2): 368–378. DOI: https://doi.org/ 10.1007/s11771-018-3743-6.
1 Introduction
At present a massive number of mountainous tunnels have been excavated in practical engineering projects and a large number of collapses often occur to the shallow tunnels. The collapse of the tunnel exerts great threats to both the life and property of the constructors [1]. In order to avoid the loss of the collapse of the shallow tunnels, different sorts of theoretical calculation methods for predicting the stability of shallow tunnels are used nowadays.
Among a large number of methods which are suitable for solving the stability problem of shallow tunnels, limit equilibrium method, finite element theory and the limit analysis method are widely used. Due to the limitations of the limit equilibrium method and finite element theory, the limit analysis method becomes increasingly popular to evaluate the stability problems. In 1970’s the upper bound theorem was proposed by CHEN [2]. Then this theorem had great importance in the field of geotechnical engineering because of its great validity in dealing with the stability problems in underground structures. By establishing three dimensional failure mechanisms, LECA and DORMIEUX [3] used the limit analysis method and model test to prove that the mode is rational in 1990. On the basis of the previous work, SOUBRA [4] proposed a new failure mode to examine the face stability of the shallow tunnel and the results had a great improvement. In 2009, the three-dimensional face stability of the shallow buried circular tunnel was analyzed by MOLLON et al [5] with the help of the combination of the reliability analysis and limit analysis. YANG et al [6] studied the influences of dilatancy angle on the stability by limit analysis method. YANG and QIN [7] put forward a new failure mechanism of shallow tunnels by considering the seepage effects. The upper bound theorem will be illustrated at length in the following.
By considering the nonlinear mechanical characteristics of geotechnical material in tunnel project, the linear criterion which is used to evaluate the stability of the tunnels has been replaced by the nonlinear criterion [8–11]. During the process of applying nonlinear failure criterion, a generalized tangential methodology was suggested [12–14] to calculate the energy dissipation rate and the external work rate accurately. At present the Hoek-Brown failure criterion [15] has been widely used among many kinds of nonlinear criterion. Especially on the basis of Hoek-Brown failure criterion FRALDI and GUARRACINO [16] used upper bound theory to characterize the collapsing shape. The curved failure mechanism was constructed according to the theory that the energy dissipation rate and external work rate were calculated along the velocity discontinuity [17]. The equation about it will be set in the following.
In terms of shallow tunnels, the ground water plays a significant role in the stability of underground structures. However, the effect of water pressures and seepage forces were ignored in the stability analysis in some scholars’ researches by considering the fact that piles of underground structures were located in the saturated stratum. WANG et al [18] found that there exists an optimum size for grouting zone to support pressure. HUANG et al [19] used the approach of conformal mapping to obtain the analytical solution to steady ground water flowing into a horizontal tunnel. FENG et al [20] put forward that the crown and bottom of underwater shield tunnel with large profile are liable to collapse by model test. Based on what mentioned above, the seepage forces and surface settlement would be considered in this work.
According to the introduction of the previous works which are on the basis of the condition that the tunnel is buried in single rock layer, some kinds of tunnels excavated in layered strata determined by different material parameters should not be ignored in engineering. Furthermore, the seepage forces and surface settlement should be regarded as external loading in the limit analysis. So the new failure mechanism consisting of two different functions which describe two rock layers is suggested in this work. As shown in Figure 1, the failure mechanism is made up of two curves, y=f(x) and y=g(x) in the symmetrical coordinate system. A, B, σc, σt and ρ are geotechnical parameters. L1 is the width of collapsing block around the circumference of tunnel lining, L2 is the width of the collapse block of lower rock layer. h1 is the height of the collapse block in the upper rock, h2 is the height between the tunnel roof and the layered position, R is the radius of the circular tunnel, sm is the maximum surface settlement, q is the supporting force on the tunnel. Based on the study by YANG and YAN [21], this work is to explore the influences of the parameters in the nonlinear failure criterion and pore water coefficient on shallow tunnel in the layered strata.

Figure 1 Curved failure mechanism of shallow tunnels buried in layered strata
2 Limit analysis with Hoek-Brown criterion
2.1 Upper bound theorem
The theory of the upper bound has been widely used to the predictions of the stability of the tunnels. The upper bound theorem of limit analysis can be depicted as: when the velocity boundary conditions and consistency conditions for strain and velocity are satisfied by the maneuvering-allowable velocity field which is built, the actual loads should be no more than the values of the calculated loads which are derived from the equation constituted by equating the external rate of work and the rates of the internal energy dissipation.
According to CHEN [2], the upper bound theorem with seepage forces effect can be written as follows:
 (1)
(1)
where σij is the stress tensor, is the strain rate in the kinematically admissible velocity field, respectively. Ti is the limit load exerted on the boundary surface. S is the length of velocity discontinuity, Xi is the body force which is caused by weight, V is the volume of the plastic zone, vi is the velocity along the velocity discontinuity surface.
is the strain rate in the kinematically admissible velocity field, respectively. Ti is the limit load exerted on the boundary surface. S is the length of velocity discontinuity, Xi is the body force which is caused by weight, V is the volume of the plastic zone, vi is the velocity along the velocity discontinuity surface.
2.2 Nonlinear Hoek-Brown failure criterion
Numerous experiments have shown that the shear stress and normal stress have nonlinear relation in geotechnical materials’ failure. Let the Hoek-Brown generalized criterion be written in the Mohr’s plane σn–τn,

 (2)
(2)
where A and B are dimensionless parameters characterizing the rock mass; σc and σt are the compressive and tensile stresses at failure, respectively.
Especially a straightforward mechanical interpretation of the coefficient A can be easily given when the Hoek-Brown criterion is made coincident with Mohr-Coulomb failure criterion,  that is
that is

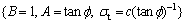 (3)
(3)
where f represents the angle of internal friction and c is the cohesion of the rock mass.
In the framework of standard plastic materials, such as those obeying to an associated flow rule, 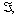 to be coincident with the Hoek-Brown yield curve and considering the half-plane where τn is positive, it is
to be coincident with the Hoek-Brown yield curve and considering the half-plane where τn is positive, it is
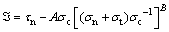 (4)
(4)
So that the plastic strain rate can be written as follows:
 (5)
(5)
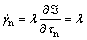 (6)
(6)
where λ is a scalar parameter.
From Eqs. (5) and (6), the normal component of stress can be written as a function of the Hoek-Brown mechanical parameters and of the first derivative of the unknown detaching curve,f ′(x), that is
 (7)
(7)
where σn is the normal stress on the failure surface.
3 Upper bounder analysis and variational approach
Many scholars have studied the progressive failure modes of the deep tunnel roof with arbitrary cross sections in layered rocks. By considering the fact that a large number of shallow-buried tunnels are also constructed in the layered strata, this work investigates the failure mechanism of shallow tunnels in layered rocks considering the seepage forces and surface settlement. The upper bound solutions derived from this work have general applicability and can be used more widely. Due to the geometric difference between the velocity discontinuity lines, the boundary conditions along the detaching lines should be satisfied to make sure the geometry continuity. In order to get the upper bound solutions to describe the shape of the collapsing block, the first work is to calculate the internal energy dissipation rate produced by the shear stress and normal stress along the two different detaching lines. Furthermore, the objective function consisting of the internal and external work should be constructed. Lastly two failure shape curves y=f(x) and y=g(x) can be obtained by the variational approach.
3.1 Assumptions for analysis
The failure shape of the collapsing block, as illustrated in Figure 1, should be obtained with conditions. Given the behavior of the layered rocks which are subjected to seepage forces should be ideally plastic and follow an associated flow rule, that is, the stress points of the ideally plastic soils should not exceed the yield surface. The width of collapsing block at the ground level, 5i, is only determined by the depth from the center of tunnel to ground surface. Moreover, the relationship of the i and H0 can be described as i=k·H0, where i stands for the distance between the tunnel centerline and the point of the trough inflexion, H0 is the depth of the center of tunnel, k is a coefficient. By considering the shape of the collapsing block to be symmetrical with respect to the y-axis, the profile of the detaching curves should be smooth and continuous. The collapsing block can be seen as a rigid block without considering the arch effect of shallow circle tunnels.
3.2 Computation of internal energy dissipation rate
From the assumptions above, the two plastic potential functions of two rock strata are
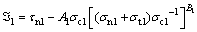 (8)
(8)
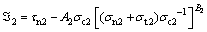 (9)
(9)
where “1” and “2” in the subscript of the parameters stand for the upper rock layer and lower one, respectively. The plastic strain increment is proportional to the gradient of the plastic potential function through the associated flow rule. It can be concluded that the normal stresses of any point on the velocity discontinuity are
 (10)
(10)
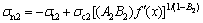 (11)
(11)
where f(x) is the function of velocity discontinuity surface in the upper layer and f′(x) is the first derivative of f(x). g(x) is the equation of velocity discontinuity surface in the lower soil and g′(x) is the first derivative of g(x).
During the process of the impending collapse, the dissipation densities of the internal forces on the detaching surface,  and
and 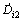 , are
, are

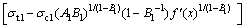 (12)
(12)

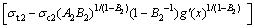 (13)
(13)
where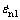 and
and are normal plastic strain rates respectively,
are normal plastic strain rates respectively, 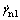 and
and are shear plastic strain rates respectively, w is the thickness of the plastic detaching zone, and v is the velocity of the collapsing block.
are shear plastic strain rates respectively, w is the thickness of the plastic detaching zone, and v is the velocity of the collapsing block.
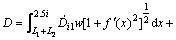
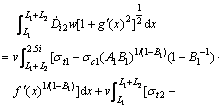
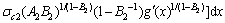 (14)
(14)
3.3 Calculation of external power
The work rate of failure block produced by weight can be calculated by integral process

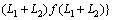 (15)
(15)
where 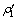 and
and  are the buoyant weight per unit volume of the upper and lower rocks, respectively.
are the buoyant weight per unit volume of the upper and lower rocks, respectively.
ρ′=ρ–ρw, in which ρ is the weight per unit volume of the rock, and ρw is the unit weight of water. The function c(x) is the function describing the circular tunnel profile. s(x) characterizes the shape of surface settlement.
The distribution of excess pore pressure which is derived from the study of Refs. [22–25] can be written as
 (16)
(16)
where p is the pore water pressure at the considered point which can be obtained by a suitable method p=ruρh, ru stands for pore pressure coefficient, and pw=ρwh is the hydrostatic distribution for pore pressure, h is the vertical distance between the roof of the tunnel and the top of the failure block. So –grad u can be defined as
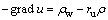 (17)
(17)
Therefore, the work rate produced by seepage forces along the velocity discontinuity surface is

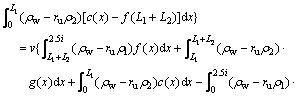
 (18)
(18)
As the tunnel is constructed in the shallow stratum, the supporting structure is inevitable for the purpose of safety and stability. Therefore, the work rate of supporting pressure in the shallow circular tunnel is
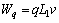 (19)
(19)
where q is the supporting pressure exerting on the circumference of tunnel lining. In the meantime, underground structure is usually under the effect of external force put on the ground surface, so the work rate of extra force can be computed as
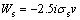 (20)
(20)
where σs stands for the surcharge load put on the ground surface.
3.4 Upper bound solutions of size of collapse block
According to the upper bound theorem, the solution which is obtained from the virtual work function seems to be more close to real limit solution in any kinematic admissible velocity field. In order to get the optimal upper bound solution, it is required to make an objective function by the external and internal rate of work. The function can be expressed as
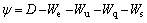 (21)
(21)
Substituting Eqs. (14), (15), (18), (19) and (20) into Eq. (21), the expression of objective function is given


 (22)
(22)
in which
 (23)
(23)
 (24)
(24)
The expressions of and
and 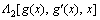 can be shown as
can be shown as
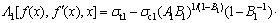
 (25)
(25)
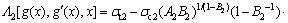
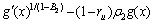 (26)
(26)
In order to get the extremum of the objective function ψ, it is necessary to search for the extremum values of objective functions Λ1 and Λ2. Because of the similarity of the expressions of Λ1 and Λ2 the process of obtaining optimal upper solution of ψ is treated as seeking for the minimum values of Λ1 and Λ2, respectively. During this process, the variational method must be used, that is, the expressions of Λ1 and Λ2 should be turned into two Euler’s equations through the variational method. The expressions of variational equations of Λ1 and Λ2 on stationary conditions can be written as
 (27)
(27)
 (28)
(28)
By the variational calculation, the explicit forms of the two Euler’s equations for the Eqs. (25) and (26) can be obtained as

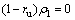 (29)
(29)
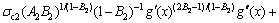
 (30)
(30)
Obviously, Eqs. (29) and (30) are two nonlinear second-order homogeneous differential equations. By the integral calculation process, the expressions of velocity discontinuity surface of upper and lower soil strata are
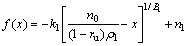 (31)
(31)
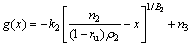 (32)
(32)
in which
 (33)
(33)
 (34)
(34)
where n0, n1, n2 and n3 stand for the integration constants coefficients determined by mechanical and geometric boundary conditions, respectively.
From what mentioned above, given the detaching curves are supposed symmetric with respect to the y-axis. It can be seen from the Figure 1 that the shear stress on the ground surface equals zero at the point which its x-height is 2.5i.
 (35)
(35)
Furthermore, the explicit expressions of the function of velocity discontinuity surface should fulfill other boundary conditions. Such as,
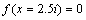 (36)
(36)
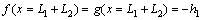 (37)
(37)
 (38)
(38)
For the purpose of keeping the whole curve look smooth, another boundary condition should be satisfied,
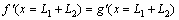 (39)
(39)
The explicit values of n0, n1, n2 and n3 can be derived from Eqs. (35), (36), (37) and (39) above. Building on this results, the expressions of the function of velocity discontinuity surface can be obtained,
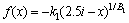 (40)
(40)
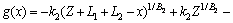
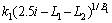 (41)
(41)
in which
 (42)
(42)
On the basis of the expression of the profile of the circular tunnel, the piece of external work can be calculated by integrating c(x) over the interval [0, L1]:
 (43)
(43)
According to the researches of Refs. [26–31], the surface settlement is defined by a Gaussian distribution curve, and the area of surface settlement trough can be obtained by calculation
 (44)
(44)
Then the expression of the objective function is
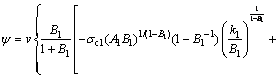

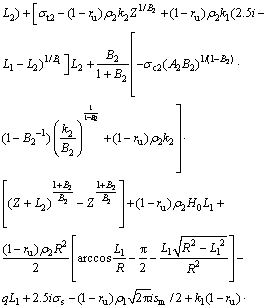
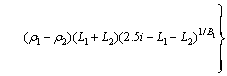 (45)
(45)
In order to get the solution which is closed to real solution, the upper bound theorem states that the solution is the extremum among the upper solutions which are determined by equating the rate of energy dissipation to the external rate of work. In other words, the objective function ψ should be zero,
Ψ=0 (46)
For the purpose of getting the explicit forms of detaching curve profile consisting of f(x) and g(x), the values of L1 and L2 must be obtained by combining and solving Eqs. (38) and (46). Then it is not difficult to draw the shape of failure surface by Eqs. (40) and (41).
3.5 Comparisons with previous work
YANG and QIN [7] put forward a curved collapse mechanism of the shallow circle tunnel with regard to surface settlement in single layered rock and a new smooth curved failure mode is constructed in two layered rocks in this work. In order to prove the effectiveness for predicting the collapse mode of tunnel roof in this work, the results of this work should be compared with others. Given the properties of the two layered rocks are the same, that is, each property parameter of two layered rocks is the same, i.e., A1=A2, B1=B2, ρ1=ρ2, σc1=σc2, σt1=σt2, the figures in two rock layers are as the same as those in single rock layer which is derived from YANG and QIN [7]. To avoid the same figures appearance, figures are not plotted for comparison.
4 Numerical results and discussion
The explicit failure surfaces of circular tunnel
profile in layered rocks can be drawn according to the analytical solutions of velocity discontinuity surfaces f(x) and g(x) which are shown as Eqs. (40) and (41). In general, the deeper the depth of the buried circular tunnel is, the better the nature of the rock is. So the relationships of the parameters between two rock layers are A1
4.1 Effects of parameters in Hoek-Brown criterion on failure mechanisms
In order to explore the influence of different parameters in Hoek-Brown criterion such as A1, A2, B1 and B2 on the shape of roof collapse, the tunnel which is subjected to seepage forces in two different layered strata should be considered. At the same time, other factors should be fixed. Figure 2 shows the failure mechanism of tunnel roof corresponding to σt1=18 kPa, σt2=24 kPa, σc1=2.1 MPa, σc2=2.1 MPa, ρ1=16 kN/m3, ρ2=18 kN/m3, σs=80 kPa, R=5 m, H0=10 m, sm=0.2 m, q=700 kPa, ru=0.1, h1=2 m. According to the Figure 2, it can be obviously seen that the width of collapsing block around the circumference of tunnel lining tends to decrease with the increase of parameters A1 and A2. However, the figure shows totally contrary results about the influence of parameters B1 and B2 on the L1. When A1 and A2 are fixed, the value of the width of collapsing block around the circumference of tunnel lining presents to be larger with the increase of B1 and B2. The size of the failure collapsing block varies more slightly with the change of parameters in lower rock layer. In other words, the parameters in upper rock layer have larger influence on the size of the collapse block than those in lower stratum. From the perspective of engineering, the nature of the rock in upper soil layer is worse than that in lower one, so the parameters in upper rock layer make a larger contribution to the failure block.

Figure 2 Effects of parameter in Hoek-Brown criterion on failure mechanisms of shallow tunnel in layered rocks:
4.2 Effects of unit weights on failure mechanisms
The unit weight of rocks plays a significant role in the shape and size of the collapse block. When other parameters are fixed, i.e., A1=0.4, A2=0.6, σc1=2.1 MPa, σc2=2.1 MPa, ρ1=16 kN/m3, ρ2=18 kN/m3, σs=80 kPa, R=5 m, H0=10 m, sm=0.2 m, q=700 kPa, ru=0.1, h1=2 m, the size of the collapse block increases with the increase of the unit weights in different rock layers. The figure shows that the unit weight ρ1 in upper rock layer makes a bigger influence than ρ2 which is the unit weight in lower rock layer. From the perspective of engineering, the shallow-buried tunnels excavated in the layered rocks with low values of unit weight will contribute to controlling the size of failure block.
By calculating the scope of the collapsing blocks considering the joined effects of the seepage forces and surface settlement with the fixed parameters, the upper bound solutions of the size of the collapsing blocks are listed in the figure below. According to Table 1, it can be obviously concluded that the values of L2 is inverse proportion to those of L1 to some extent.
4.3 Effects of pore pressure coefficient on failure mechanisms
The influence of the seepage forces on the stability of the surrounding rock of the tunnel roof is great during the process of the shallow tunnel excavation in the underground engineering. Due to the fact that the seepage forces make an adverse influence on the shallow-buried tunnels constructions, it is difficult to ignore the effect of the pore pressure coefficient on the shape of the collapsing block. The tunnel which is subjected to seepage forces in two different layered strata is considered with a nonlinear yield criterion in this work. Figure 4 shows the failure mechanism of tunnel roof corresponding to A1=0.7, A2=0.8, B1=0.6, B2=0.9, σc1=150 kPa, σc2=240 kPa, σt1=2.0 kPa, σt2=2.4 kPa, ρ1=18 kN/m3, ρ2=23 kN/m3, σs=50 kPa, R=5 m, Z0=15 m, sm= 0.1 m, q=1500 kPa, h1=5.5 m.

Figure 3 Effects of unit weight on failure mechanisms of shallow tunnel in layered rocks:
Table 1 Upper bound solutions of size of collapsing blocks of shallow tunnel in layered soils
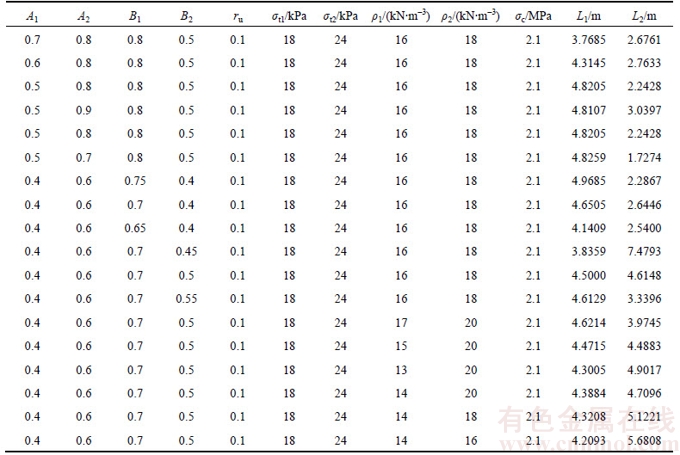
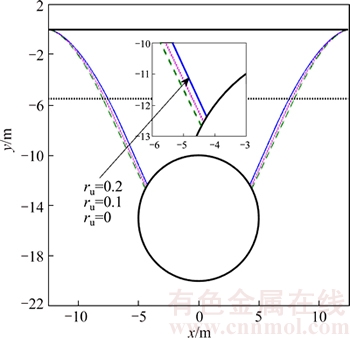
Figure 4 Effects of pore pressure coefficient on failure mechanisms of shallow tunnel in layered rocks
According to the Figure 4, it can be concluded that the collapsing width tends to decrease with the increase of the pore pressure coefficient.
The aim of this work is to investigate the stability of the shallow tunnels considering surface settlement and seepage forces in layered strata. Although the multi layered rocks are not discussed in the preceding analysis, the method used in this work is also applicable to the case of multi layered strata.
5 Summary and conclusions
On the basis of previous work which has focused the efforts on the collapse mechanism in single rock stratum, a new curved failure mechanism of circular tunnel considering seepage force and surface settlement is proposed to estimate the stability of tunnel roof under a limit state. With Hoek-Brown failure criterion and upper bound theory, the numerical solution for the shape of collapse mechanism is obtained by setting an objective function consisted of energy dissipation rate and the external work rate. Some conclusions are drawn:
1) With the increase of the parameter A in Hoek-Brown failure criterion, the value of the width of collapsing block around the circumference of tunnel lining presents to decrease. In the contrast, the parameter B shows contrary law on it. Moreover, the size of the failure collapsing block varies more slightly with the change of parameters in lower rock layer than that in upper rock layer owing to the fact that the nature of the rock in upper layer is worse than that in lower one.
2) The collapsing width tends to decrease with the increase of the pore pressure coefficient while the unit weight in different rock layers has a positive correlation with the scope of roof collapse.
References
[1] FRALDI M, GUARRACINO F. Analytical solutions for collapse mechanisms in tunnels with arbitrary cross sections [J]. International Journal of Solids and Structures, 2010, 47(2): 216–223.
[2] CHEN W F. Limit analysis and soil plasticity [M]. Amsterdam: Elsevier, 1975: 47–99.
[3] LECA E, DORMIEUX L. Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material [J]. Geotechnique, 1990, 40(4): 581–606.
[4] SOUBRA A H. Three-dimensional face stability analysis of shallow circular tunnels [C]// Proceedings of the International Conference on Geotechnical and Geological Engineering. Melbourne, Australia, 2000: 19–24.
[5] MOLLON G, DIAS D, SOUBRA A H. Probabilistic analysis of circular tunnels in homogeneous soil using response surface methodology [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(9): 1314–1325.
[6] YANG X L, XU J S, LI Y X, YAN R M. Collapse mechanism of tunnel roof considering joined influences of nonlinearity and non-associated flow rule [J]. Geomechanics and Engineering, 2016, 10(1): 21–35.
[7] YANG X L, QIN C B. Limit analysis of rectangular cavity subjected to seepage forces based on Hoek-Brown failure criterion [J]. Geomechanics and Engineering, 2014, 6(5): 503–515.
[8] MOLLON G, DIAS D, SOUBRA A H. Rotational failure mechanisms for the face stability analysis of tunnels driven by a pressurized shield [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2011, 35(12): 1363–1388.
[9] YANG X L, YAO C. Stability of tunnel roof in nonhomogeneous soils [J]. International Journal of Geomechanics, 2018, 18(3): 06018002. DOI: 10.1061/ (ASCE)GM.1943- 5622.0001104.
[10] YANG X L. Lower bound analytical solution for bearing capacity factor using modified Hoek–Brown failure criterion [J]. Canadian Geotechnical Journal, 2018. DOI: 10.1139/cgj- 2016-0694.
[11] YANG X L, ZHANG R. Limit analysis of stability of twin shallow tunnels considering surface settlement [J]. KSCE Journal of Civil Engineering, 2017. DOI: 10.1007/s12205- 017-1398-8.
[12] XU J S, YANG X L. Effects of seismic force and pore water pressure on three dimensional slope stability in nonhomogeneous and anisotropic Soil [J]. KSCE Journal of Civil Engineering, 2017. DOI: 10.1007/s12205-017-1958-y.
[13] LI T Z, YANG X L. Risk assessment model for water and mud inrush in deep and long tunnels based on normal grey cloud clustering method [J]. KSCE Journal of Civil Engineering, 2017. DOI: 10.1007/s12205-017-0553-6
[14] YANG X L, LI Z W, LIU Z A, XIAO H B. Collapse analysis of tunnel floor in karst area based on Hoek-Brown rock media [J]. Journal of Central South University, 2017, 24(4): 957–966.
[15] HOEK E, BROWN E T. Practical estimates of rock mass strength [J]. International journal of Rock Mechanics and Mining Sciences, 1997, 34(8): 1165–1186.
[16] FRALDI M, GUARRACINO F. Limit analysis of collapse mechanisms in cavities and tunnels according to the Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(4): 665–673.
[17] SUBRIN D, WONG H. Tunnel face stability in frictional material: A new 3D failure mechanism [J]. Computes Mechanique, 2012, 330(7): 513–519.
[18] WANG X Y, TAN Z S, WANG M S, ZHANG M, HUANG F M. Theoretical and experimental study of external water pressure on tunnel lining in controlled drainage under high water level [J]. Tunnelling and Underground Space Technology, 2008, 23(5): 552–560.
[19] HUANG F M, WANG M S, TAN Z S, WANG X Y. Analytical solutions for stead seepage into an underwater circular tunnel [J]. Tunnelling and Underground Space Technology, 2010, 25(4): 391–396.
[20] FENG K, HE C, ZHOU J M, ZHANG Z. Model test on impact of surrounding rock deterioration on segmental lining structure for underwater shield tunnel with large cross-section [J]. Procedia Environmental Sciences, 2012, 12: 891–898.
[21] YANG X L, YAN R M. Collapse mechanism for deep tunnel subjected to seepage force in layered soils [J]. Geomechanics and Engineering, 2015, 8(5): 741–756.
[22] SAADA Z, MAGHOUS S, GARNIER D. Stability analysis of rock slopes subjected to seepage forces using the modified Hoek-Brown criterion [J]. International Journal of Rock Mechanics and Mining Sciences, 2012, 55(1): 45–54.
[23] OSMAN A S. Stability of unlined twin tunnels in undrained clay [J]. Tunnelling and Underground Space Technology, 2010, 25(2): 290–296.
[24] Xu J S, Li Y X, Yang X L. Stability charts and reinforcement with piles in 3D nonhomogeneous and anisotropic soil slope [J]. Geomechanics and Engineering, 2018, 14(1): 71–81.
[25] XU J S, PAN Q J, YANG X L, LI W T. Stability charts for rock slopes subjected to water drawdown based on the modified nonlinear Hoek-Brown failure criterion [J]. International Journal of Geomechanics, 2018, 18(1): 04017133.
[26] LEE I M, NAM S W. The study of seepage forces acting on the tunnel lining and tunnel face in shallow tunnels [J]. Tunnelling and Underground Space Technology, 2001, 16(1): 31–40.
[27] NAKAMURA H, KUBOTA T, FURUKAWA M, NAKAO T. Unified construction of running track tunnel and crossover tunnel for subway by rectangular shape double track cross-section shield machine [J]. Tunnelling and Underground Space Technology, 2003, 18(2, 3): 253–262.
[28] YANG X L. Effect of pore-water pressure on 3D stability of rock slope [J]. International Journal of Geomechanics, 2017, 17(9): 06017015. DOI: 10.1061/(ASCE)GM.1943-5622. 0000969.
[29] YANG X L, ZHANG R. Collapse analysis of shallow tunnel subjected to seepage in layered soils considering joined effects of settlement and dilation [J]. Geomechanics and Engineering, 2017, 13(2): 217–235.
[30] YANG Z H, ZHANG R, XU J S, YANG X L. Energy analysis of rock plug thickness in karst tunnels based on non-associated flow rule and nonlinear failure criterion [J]. Journal of Central South University, 2017, 24(12): 2940–2950.
[31] LI T Z, LI Y X, YANG X L. Rock burst prediction based on genetic algorithms and extreme learning machine [J]. Journal of Central South University, 2017, 24(9): 2105–2113.
(Edited by HE Yun-bin)
中文导读
沉降与渗流联合作用下层状地层浅埋隧道运动分析
摘要:极限分析是一种预测岩土工程稳定性的重要工具。近年来随着隧道工程的发展,关于浅埋隧道开挖中地下水对隧道顶部稳定性的研究越来越重要。在本文中,作者探究了孔隙水压力和表面地表沉降共同作用下浅埋隧道顶部在层状岩层中的破坏模式。本研究应用上限分析理论,并采用Hoek-Brown 非线性破坏准则来探索不同因素对浅埋隧道破坏模式和支护系统的影响。以双层岩层为例,通过两条不同的非线性破坏面的引入,本文得到了描述层状岩石层中不同的隧道破坏模式。本文另一创新是通过固体力学变分法得到强非线性方程,并通过数值方法得到浅埋隧道的破坏模式。另外本文深入探索了不同参数对隧道破坏模式的影响。通过数据和画图的形式讨论了不同因素对隧道破坏模式的影响。
关键词:破坏机制;层状岩体;Hoek-Brown准则;渗流力;表面沉降
Foundation item: Project(51378510) supported by the National Natural Science Foundation of China; Project(2017zzts157) supported by the Innovation Foundation for Postgraduate of Central South University, China
Received date: 2016-05-13; Accepted date: 2017-12-05
Corresponding author: LU Si-ping, PhD, Lecturer; Tel: +86–13787102817; E-mail: 345766359@qq.com, siping1018@126.com

