Trans. Nonferrous Met. Soc. China 22(2012) 634-641

Constitutive model for a new kind of metastable β titanium alloy

during hot deformation

WANG Zhe-jun, QIANG Hong-fu, WANG Xue-ren, WANG Guang

Xi’an Hi-tech Institute, Xi’an 710025, China

Received 7 March 2011; accepted 5 November 2011

Abstract: The constitutive model was developed to describe the relationship among flow stress, strain, strain rate, and deformation temperature completely, based on the characteristics of flow stress curves for a new kind of metastable β Ti2448 titanium alloy from isothermal hot compression tests, in a wide range of temperatures (1023-1123 K) and strain rates (63-0.001 s^-1). During this process, the adopted hyperbolic sine function based on the unified viscoplasticity theory was used to model the flow behavior of alloy undergoing flow softening caused by dynamic recovery (DRV) at high strain rates (≥1 s^-1). The standard Avrami equation was adopted to represent the softening mechanism attributed to dynamic recrystallization (DRX) at low strain rates (<1 s^-1). Additionally, the material constants were determined by optimization strategy, which is a new method to solve the nonlinear constitutive equation. The stress—strain curves predicted by the developed constitutive model agree well with the experimental results, which con?rms that the developed constitutive model can give an accurate estimate of the ?ow stress of Ti2448 titanium alloy and provide an effective method to model the flow behavior of metastable β titanium alloys during hot deformation.

Key words: metastable β titanium alloy; hot compression; dynamic recovery; dynamic recrystallization; constitutive model

1 Introduction

Metastable β titanium alloys are used for a wide variety of aerospace applications owing to their high strength-to-density ratio, good hardenability, excellent fatigue performance, crack-propagation and corrosion resistance. So, more and more attention has been paid to these alloys in many countries [1]. Up to now, related researches have been mostly carried out on the flow behavior of metastable β titanium alloys during hot deformation [2-4], and limited information is available on the constitutive model which can describe the relationship among flow stress, strain, strain rate, and deformation temperature completely.

Constitutive model is important for simulating the hot forming processes because of its effective role in describing the flow behavior of materials. Recently, plenty of experimental and theoretical works have been conducted and a number of models have been proposed for steel, magnesium, and aluminum alloys which can predict the flow stress validly. But it is still a difficult task to develop a model for titanium alloys to reflect the deformation mechanism and describe the relationship among flow stress, strain, strain rate, and deformation temperature completely, because the ?ow behavior is often so complex at hot deformation condition. The Arrhenius equation is most widely used to describe the relationship among flow stress, strain rate, and deformation temperature, especially at high temperatures [5-7]. However, the effects of strain on the flow stress are not considered in this equation, which limits its application [8]. CAI et al [9] proposed a model where the in?uence of strain on the flow stress was incorporated by considering the effect of strain on material constants. NIU et al [10] proposed constitutive model based on the arti?cial neural network approach. Though these models can predict the ?ow stress of titanium alloys accurately, they are not able to offer physical insight. LI et al [11] proposed a multi-scale constitutive model based on the internal state variable approach and the microstructure evolution of titanium alloys during hot deformation. But it is often very difficult for many investigators without the precision apparatuses and the use is limited due to its complexities. It is an effective way to develop a constitutive model that can reflect the deformation mechanism, and the material constants can be calculated easily based on the characteristics of flow stress curves.

The objective of the present work is to formulate a suitable constitutive model to predict the high temperature flow behavior of metastable β titanium alloys by analyzing the influences of strain, strain rate, and deformation temperature on flow stress, based on the characteristics of flow stress curves. Toward this, isothermal hot compression tests were conducted on a new kind of metastable β Ti2448 titanium alloy in a wide range of strain rates and temperatures. The experimental data were then employed to determine material constants in the constitutive model. Finally, the validity of the developed constitutive model was also examined over the entire experimental ranges by comparison of the experimental and predicted results.

2 Experimental

The material used in the present investigation, named Ti2448 alloy, has been developed recently at Shenyang National Laboratory for Materials Science, Institute of Metal Research, Chinese Academy of Sciences. And its chemical composition (mass fraction) is 24.2%Nb-3.9%Zr-7.8%Sn-0.11%O-0.008%N [12]. The compression specimens with 12 mm in height and 8 mm in diameter were machined from the as-received industrially ingots.

The specimens were heated to the applied temperature with the speed of 10 °C/s and held at the temperature for 5 min before deformation to a true strain of 0.6. The compression tests were carried out on a Gleeble-3800 simulator in the temperature range of 750-850 °C at an interval of 50 °C and constant true strain rates of 0.001, 0.01, 0.1, 1, 10 and 63 s^-1. Then, specimens were rapidly quenched in water to preserve the microstructure after hot deformation. The deformed structures were sectioned parallel to the compression axis along the direction of centerline and prepared by the conventional methods for the microstructural observations.

3 Results and discussion

The typical microstructures of the deformed samples under different hot deformation conditions are shown in Fig. 1. Figure 1(a) shows the microstructure of original state, which is equiaxed. Figures 1(b) and (c) show the as-deformed state at 1023 K and strain rates of 10, 0.01 s^-1, respectively. At a high strain rate, the deformed ones elongated perpendicularly to the compression direction (as arrowed in Fig.1 (b)) and without any new grains formed, which implies that the softening mechanism of this alloy is dynamic recovery rather than dynamic recrystallization. Whereas at a lower strain rate, a large of new recrystallization grains are formed in the grain and the microstructure is typical for dynamic recrystallization.

Fig. 1 Microstructures of Ti2448 titanium alloy: (a) Original state; (b) As-deformed state at 1023 K and 10 s^-1; (c) As-deformed state at 1023 K and 0.01 s^-1

In Fig. 2, the solid lines show the true stress—true strain curves of Ti2448 obtained from the tests conducted. The characteristics of flow stress curves are represented as follows.

At a given temperature, the flow stress increases as strain rate increases. In the same way, at a given strain rate, the flow stress decreases as temperature increases. So, the influence of temperature and strain rate on flow stress is significant. In the first deformation period, the flow stress rises with strain increasing rapidly, illuminating that the work-hardening plays the major role. With the deformation process going on, the curves exhibit two main shapes.

At high strain rates (≥1 s^-1), the curves present a small hardening transient which develops into a saturation state subsequently at the true strain range of 0.1-0.3 when the hardening rate is equal to the softening rate. But at strain rates of 63 and 10 s^-1, the values of saturation stress do not keep constant and there is a further drop in stress—strain curves, which is caused by the change of deformation temperature and will be discussed in the next section. It can also be seen that the flow stress curves wave at high strain rates, which is caused by the interaction between flow hardening and softening in the microstructure [13]. But at the strain rate of 63 s^-1, the more significant oscillation is due to not only this interaction, but also other complicated reasons. On one hand, this phenomenon may stand for the unstable flow at faster strain rates, which corresponds to the inhomogeneous deformation such as occurring of adiabatic shear bands and ?ow localization [14,15]. On the other hand, it may be caused by the limit of loading rate of the Gleeble-3800 simulator. Because the strain rate of 63 s^-1 is close to its maximal value of 70 s^-1, the data may be affected during the experiment. When the isothermal compression was conducted at the strain rate of 50 s^-1 and temperature of 700 °C, one can also see the significant oscillation in the flow stress curve. And the oscillation is more significant than that at strain rate of 10 s^-1, but less than 63 s^-1, which implies that the above analyses are reasonable. In view of the complexity at strain rate of 63 s^-1, further research should be conducted. When calculating, the average values were used at strain rate of 63 s^-1, in the case of keeping the trend of the stress—strain curves.

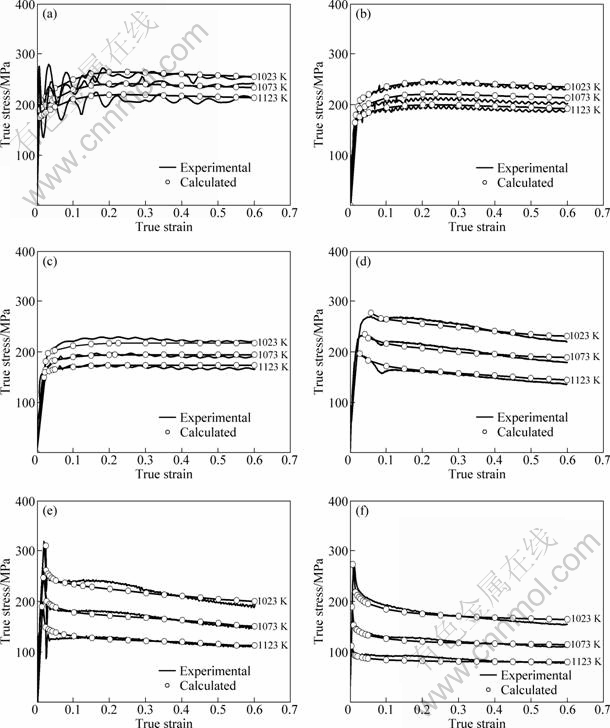
Fig. 2 True stress—true strain curves of Ti2448 alloy at different strain rates: (a) 63 s^-1; (b) 10 s^-1; (c) 1 s^-1; (d) 0.1 s^-1; (e) 0.01 s^-1;  (f) 0.001 s^-1

Whereas at low strain rates (<1 s^-1), the flow stress drops rapidly and all curves exhibit an initial sharp peak, i.e. discontinuous yielding [3]. After this peak, the continuous softening behavior and steady-state ?ow can be observed at a strain rate of 0.001 s^-1. But at the strain rates of 0.1 and 0.01 s^-1, discontinuous yielding is followed by a slight degree of strain hardening, ?ow softening and eventually steady-state ?ow.

Based on the above analysis and a lot of previous researches [16,17], the dominating softening mechanism is DRV at high strain rates and DRX at low strain rates, respectively.

4 Modeling of flow stress

4.1 Modeling of flow stress at high strain rates

It is generally accepted to use the hyperbolic sine law proposed by SELLARS and TEGART to model the temperature and strain rate dependence of flow stress at any given strain [8]. A unified viscoplastic constitutive model has been developed to predict the deformation behavior of a class of titanium alloys undergoing deformation through a range of mechanism [18-22]. So, the adopted hyperbolic sine function based on the viscoplastic theory can be developed as a model to describe the relationship between flow stress and strain, and to reflect the flow behavior of Ti2448 titanium alloy affected by both strain rate and deformation temperature during hot deformation. In this model, the softening effect due to DRV at high strain rates (≥1 s^-1) is also considered [21].

In the case of uniaxial compression, the total strain rate is assumed to be decomposed into an elastic part and a plastic part. The expression is written as:

                                 (1)

When the elastic deformation is ignored compared with plastic deformation, the strain rate  can be defined as a hyperbolic sine function of flow stress σ and the internal variable s, as follows [21]:

               (2)

                           (3)

where σ₀ is the yield stress, which depends on the strain rate and deformation temperature; A, n are material constants; T is the thermodynamic temperature (K); R is the mole gas constant (8.31 J/(mol·K)); Q is the activation energy of hot deformation (J/mol); s is the internal variable which represents isotropic hardening of materials and expends the yield surface obeying the von Mises yield criterion; s_M is the internal variable which represents that the microstructures and dislocation densities would no longer vary with deformation and a saturated state is obtained; b^*, m^* are two parameters that depend on temperature and strain rate [21]. Solving  Eqs. (2) and (3) yields:

         (4)

Z=εexp[-Q/(RT)]                             (5)

with b=b^*/(m^*+1) and m=m^*+1, where Z is the Zener-Hollomon parameter proposed by ZENER and HOLLOMON, and is a factor of strain rate compensated by temperature [23].

In Eq. (4), the higher the parameter b is, or the lower the parameter m is, the quicker the stress becomes saturated, which is similar to the effect of strain rate and deformation temperature on stress—strain curves. The lower the strain rate is, or the higher the temperature is, the easier the stress—strain curves obtain a saturated state. The hardening transient is more clearly observed at high strain rates and low deformation temperatures. So, b and m can be expressed as a function of Zener-Hollomon parameter in the present model to reflect the effects of strain rate and deformation temperature on stress—strain curves, as follows:

                                (6)

                              (7)

where Z_b, Z_m are Zener-Hollomon parameter; k_b, k_m, n_b and n_m are materials constants.

As a result of dynamic equilibrium of hardening and dynamic recovery, a steady state or saturated flow stress should be observed in stress—strain curves. However, Fig. 2 shows that the flow stress drops slightly after the peak value at strain rates of 63 and 10 s^-1. Based on the previous studies, this is caused by the temperature rise which furthers the softening in the large plastic deformation. This effect can be ignored at lower strain rates. As the isothermal data were obtained under nearly adiabatic conditions, they must be corrected. The decrease in flow stress can be evaluated using the following expression [24]:

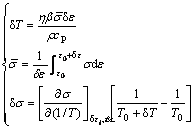              (8)

where η is the fraction of plastic work converting to heat and β is the adiabatic coefficient varying with strain and strain rate, the values of which are 0.9 and 1 in Eq. (8), respectively, according to recent reports for metals [25];  is the mean stress calculated from stress—strain curve over the strain interval δε; c_p and ρ are the speci?c heat capacity for the material and mass density, whose values are 496 J/(kg·°C) and 5.42 g/cm³, respectively. It is assumed that the temperature rise is uniform throughout the specimen and that the changes in ρ and c_p during the temperature interval δT can be neglected.

4.2 Modeling of flow stress at low strain rates

It makes the model very complicated to describe the discontinuous yielding [26] and DRX is the dominating softening mechanism of Ti2448 titanium alloy under strain rates lower than 1 s^-1, so DRX is only considered here.

When DRX takes place during hot deformation, LUTON and SELLARS [27] suggested to use an Avrami mathematical equation to characterize the volume fraction of dynamically recrystallized X as:

                          (9)

where K_A, n_A are material constants; t represents the time during a single DRX.

The Avrami equation has been modified to better describe the DRX process. When the peak strain ε_p and the critical strain ε_c for occurring of DRX are known, the time t can be expressed as [28]:

                                  (10)

Equation (10) is widely used when describing the high temperature deformation of alloys [29-30], because the peak strain ε_p can be determined from the stress—strain curve directly. And in the case of ensuring the model with high prediction, it is more convenient to calculate the volume fraction of dynamically recrystallized X by using it than other parameters, such as the strain ε_0.5 for 50% recrystallization. Based on these, in the present approach, Eq. (10) is also used.

Substituting Eq. (10) into Eq. (9), the volume fraction of dynamically recrystallized X can be written as:

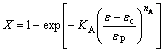                  (11)

Based on the experimental results and Ref. [8], the strain ε_p corresponding to the peak stress can be expressed as a function of strain rate and deformation temperature and defined as:

                                (12)

According to Refs. [31,32], the critical strain ε_c for occurring of DRX can be in the range of (0.6-0.85)ε_p.

In this work, the following expression gives a reasonably good fit to the data:

ε_c=0.8ε_p                                    (13)

According to Fig. 3, it is obvious that the fractional softening due to DRX can be described by the following equation:

                           (14)

where σ_drvss and σ_drv are the saturation stress and the flow stress when DRV is the only softening mechanism; σ_drxss is the steady-state stress after DRX; σ is the registered stress during DRX at hot working.

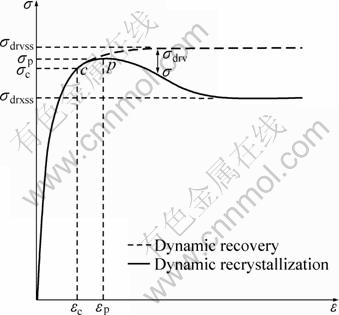
Fig. 3 True flow stress—strain curve of dynamic recovery and recrystallization (p represents where the peak stress was obtained; c represents where the DRX occurred)

According to Fig. 2, at low strain rates (<1 s^-1), the flow stress drops rapidly and all curves exhibit an initial sharp peak in the early stages of deformation. So, Eq. (14) can be written as:

                            (15)

where σ_p is the peak stress.

Hence, by combining Eq. (11) and Eq. (15), a simplified model can be developed to describe the DRX process of Ti2448 titanium alloy at hot working:

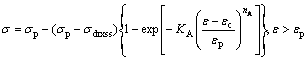                (16)

4.3 Determination of σ₀, σ_p, ε_p, σ_drxss

1) The yield stress σ₀ at high strain rate is identified on the flow stress curve in terms of a 2% offset in the total strain. At low strain rates, the peak stress σ_p, peak strain ε_p, and the steady state stress σ_drxss which is achieved at the maximal true strain can be obtained on flow stress curves directly.

2) In general, the relationship among the flow stress, strain rate and temperature of metal at any given strain during hot deformation can be expressed by the hyperbolic-sine meliorated Arrhenius equations as [33]:

              (17)

         (18)

          (19)

where A₁, A₂, A₃, n, n₁, α, β are material constants, which are independent of the deformed temperatures; T is the thermodynamic temperature (K);  is the strain rate; R is the gas constant (8.31 J/(mol·K)); Q is the activation energy of hot deformation; and σ is the stress at any given strain.

The relationship among α, β and n is as follows:

α=β/n                                     (20)

Substituting Eq. (5) into Eq. (17), Eq. (18) and Eq. (19), yields:

                          (21)

                    (22)

        (23)

Considering the definition of Eq. (22) and Eq. (23), the yield stress σ₀, the peak stress σ_p and the steady state stress σ_drxss can be written as follows by linear regression, respectively:

where .

4.4 Fitting and verification of constitutive model of Ti2448 titanium alloy

After modeling yield stress, peak stress and saturation stress of Ti2448 titanium alloy, the constitutive model requires the simultaneous determination of other parameters, s_M, Z, A, n, b, m (Eq. (4)), and K_A, n_A    (Eq. (16)).

The different parameters involved in the model  (Eq. (4), Eq. (16)) under consideration can be readily determined by minimizing the Euclidean distance between the experimental values and those predicted by the model via the solution of [34]:

            (24)

where x is the parameter which needs to be defined; N is the total number of experimental data, which is used in calculating; RSS is the minimum value of the objective function which corresponds to the residual sum of squares of the fit; the ‘dynamic’ subscript here refers to the rate-temperature dependence of the response.

By the Levenberg-Marquardt algorithm, the optimized values of s_M, Z, A, n, b, m (Eq. (4)) and K_A, n_A, ε_P (Eq. (16)) are listed as follows:

s_M=21.03, Z=exp(28735.77/T), n=3.80, A=3.14×10¹⁰,

b=1.12[exp(13287.56/T)]^0.21,

m=0.25[exp(13793.90/T)]^0.10, K_A=0.65, n_A=0.32,

ε_p=1.08×10^-4[exp(16743.01/ T)]^0.45.

Finally, the constitutive model of Ti2448 titanium alloy is summarized as follows.

1) At high strain rates (≥1 s^-1),

2) At low strain rates (<1 s^-1),

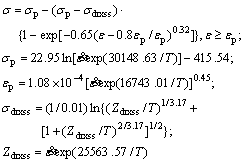
In order to verify the constitutive model, comparisons between the experimental and the predicted results were carried out. The curves with symbols in  Fig. 2 illustrate the results obtained with the application of the constitutive model. It can be obviously found that the proposed constitutive model gives an accurate estimate of the ?ow stress for Ti2448 titanium alloy under the experimental condition. But the oscillation of flow stress curves and the discontinuous yielding can not be reflected in the present model.

5 Conclusions

1) The flow behavior of a new kind of metastable β titanium alloy Ti2448 was investigated based on the hot compression tests. The experimental results indicate that the influence of deformation temperature and strain rate on flow stress is significant. At high strain rates (≥1 s^-1), the dominating softening mechanism is DRV. The flow stress after the peak value drops slightly at strain rates of 63 and 10 s^-1 due to the temperature rise. Whereas at low strain rates (<1 s^-1), the dominating softening mechanism is DRX.

2) According to characteristics of flow stress curves, the constitutive model was developed to describe the relationship between flow stress, strain, strain rate, and deformation temperature completely. During this process, the adopted hyperbolic sine function based on the unified viscoplasticity theory was used to model the flow behavior of alloy undergoing flow softening caused by dynamic recovery (DRV) at high strain rates. The standard Avrami equation was adopted to represent the softening mechanism attributed to dynamic recrystallization (DRX) at low strain rates, without considering the discontinuous yielding phenomenon at an early stage of yielding. Some of parameters may exhibit a significant dependence on strain rate and deformation temperature, which had also been considered in this model. So, the constitutive model proposed in this paper can offer physical insight and reflect the softening mechanism, such as DRV and DRX.

3) The methods to determine the material constants were developed and successfully applied to Ti2448 titanium alloy over the experimental condition. The prediction of the flow stress in Ti2448 titanium alloy as a function of strain, strain rate and deformation temperature showed to be in good agreement with the experimental results. It is concluded that the constitutive model developed can accurately describe the flow behavior of Ti2448 during hot deformation and provide an effect method for other metastable β titanium alloys.

Acknowledgements

The authors are grateful to HAO Yu-lin and TIAN Yu-xing (Institute of Metal Research, Chinese Academy of Sciences) for their cooperation and contribution to the experiment.

References

[1] IVASISHIN O M, MARKOVSKY P E, MATVIYCHUK Y V, SEMIATIN S L, WARD C H, FOX S. A comparative study of the mechanical properties of high-strength beta-titanium alloys [J]. Journal of Alloys and Compounds, 2008, 457: 296-309.

[2] ZENG Li-ying, YANG Guan-jun, GE Peng, MAO Xiao-nan, ZHAO Yong-qing, ZHOU Lian. Processing map of one kind of metastable β titanium alloy [J]. Rare Metal Materials and Engineering, 2010, 39(9): 1505-1508. (in Chinese)

[3] ZENG Li-ying, GE Peng, MAO Xiao-nan, ZHAO Yong-qing, ZHOU Lian. Hot compression behavior of one kind of metastable β titanium alloy [J]. International Journal of Modern Physics B, 2009, 23(6-7): 777-782.

[4] ZHOU Wei, GE Peng, ZHAO Yong-qing. Study on micro-structure and mechanical properties of metastable β-Ti alloy [J]. Metal Heat Treatment, 2007, 36(22): 18-23. (in Chinese)

[5] CUI W F, JINA Z, GUO A H, ZHOU L. High temperature deformation behavior of α+β-type biomedical titanium alloy Ti-6Al-7Nb [J]. Materials Science and Engineering A, 2009, 499: 252-256.

[6] HE Xiao-ming, YU Zhong-qi, LIU GUI-ming, WANG Wen-ge, LAI Xin-min. Mathematical modeling for high temperature flow behavior of as-cast Ti-45Al-8.5Nb- (W, B, Y) alloy [J]. Materials and Design, 2009, 30: 166-169.

[7] LI L X, LOU Y, YANG L B, PENG D S, RAO K P. Flow stress behavior and deformation characteristics of Ti-3Al-5V-5Mo compressed at elevated temperatures [J]. Materials and Design, 2002, 23: 451-457.

[8] LIN Y C, CHEN Xiao-min. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working [J]. Materials and Design, 2010, 32(4): 1733-1759.

[9] CAI Jun, LI Fu-guo, LIU Tai-ying, CHEN Bo, HE Min. Constitutive equations for elevated temperature ?ow stress of Ti-6Al-4V alloy considering the effect of strain [J]. Materials and Design, 2011, 32: 1144-1151.

[10] NIU Yong, LUO Jiao, LI Miao-quan. An adaptive constitutive model in the isothermal compression of Ti600 alloy [J]. Materials Science and Engineering A, 2010, 527: 5924-5929.

[11] LI Xiao-li, LUO Jiao, LI Miao-quan, SHI Yan-pei. Constitutive model for high temperature deformation of titanium alloys using internal state variables [J]. Mechanics of Materials, 2010, 42: 157-165.

[12] HAO Y L, LI S J, SUN S Y, ZHENG C Y, YANG R. Elastic deformation behavior of Ti24Nb-4Zr-7.9Sn for biomedical application [J]. Acta Biomateriallia, 2007, 3: 277-286.

[13] FANG Chao, ZHANG Jing, LIAO Ai-lin, XUE Shao-zhan, YUAN Fu-qing, PAN Fu-sheng. Hot compression deformation characteristics of Mg-Mn alloys [J]. Transactions of Nonferrous Metals Society of China, 2010, 20: 1841-1845.

[14] SEN I, RAMAMURTY U. High-temperature (1023 K to 1273 K [750 °C to 1000 °C]) plastic deformation behavior of B-modified Ti-6Al-4V alloys: Temperature and strain rate effects [J]. Metallurgical and Materials Transactions A, 2010, 41(11): 2959-2969.

[15] SESHACHARYULU T, MEDEIROS S C, FRAZIER W G, PRASAD Y V R K. Unstable flow during supratransus working of Ti-6Al-4V [J]. Materials Letters, 2001, 47: 133-139.

[16] WARCHOMICKA F, STOCKINGER M, DEGISCHER H P. Quantitative analysis of the microstructure of near β titanium alloy during compression tests [J]. Journal of Materials Processing Technology, 2006, 177: 473-477.

[17] WEISS I, SEMIATIN S L. Thermomechanical processing of beta titanium alloys-an overview [J]. Materials Science and Engineering A, 1998, 243: 46-65.

[18] SAMANTARAY D, MANDAL S, BORAH U, BHADURI A K, SIVAPRASAD P V. A thermo-viscoplastic constitutive model to predict elevated temperature flow behaviour in titanium-modi?ed austenitic stainless steel [J]. Materials Science and Engineering A, 2009, 526: 1-6.

[19] WANG X T, YAMAUCHI R, HAMASAKI H, YOSHID A F, NAGASHIMA K, MAEDA T. High temperature yield drop of β titanium alloy Ti-20V-4Al-1Sn and its modeling [J]. Current Advance in Materials Processing, 2008, 21: 703-707.

[20] ZHOU M. Constitutive modeling of the viscoplastic deformation in high temperature forging titanium alloy IMI834 [J]. Materials Science and Engineering A, 1998, 245: 29-38.

[21] ZHOU M, CLODE M P. Constitutive equations for modeling flow softening due to dynamic recovery and heat generation during plastic deformation [J]. Mechanics of Materials, 1998, 27: 63-76.

[22] LIN J, DEAN T A. Modeling of microstructure evolution in hot forming using unified constitutive equations [J]. Journal of Materials Processing Technology, 2005, 167: 354-362.

[23] ZENER C, HOLLOMON J H. Effect of strain rate upon the plastic flow of steel [J]. Journal of Applied Geophysics, 1944, 15(1): 22-32.

[24] KOBAYASHI S, OH S I, AITAN T. Metal forming and the finite element method [M]. Oxford University Press, 1989.

[25] OH S I, SEMIATIN S L, JONAS J. An analysis of the isothermal hot compress test [J]. Metallurgical Transactions A, 1992, 23(3): 963-975.

[26] PHILIPPART I, RACK H J. High temperature dynamic yielding in metastable Ti-6.8Mo-4.5F-1.5Al [J]. Materials Science and Engineering A, 1998, 243: 196-200.

[27] LUTON M J, SELLARS C M. Dynamic recrystallization in nickel and nickel-iron alloys during high temperature deformation [J]. Acta Metallurgica, 1969, 17:1033-1043.

[28] LAASRAOUI A, JONAS J. Recrystallization of austenite after deformation at high temperature and strain rates-analysis and modeling [J]. Metallurgical Transactions A, 1991, 22(7): 151-160.

[29] CHO J R, BAE W B, HWANG W J, HARTLEY P. A study on the hot deformation behavior and dynamic recrystallization of Al-5 wt.% Mg alloy [J]. Journal Materials Processing Technology, 2001, 118: 356-361.

[30] WU Chao. Study on the dynamic recrystallization behavior and prediction model of TA15 titanium alloy in the β hot process [D]. Nanchang: Nanchang Hangkong University, 2009. (in Chinese)

[31] HERMANDEZ C A, MEDINA S F, RUIZ J. Modeling austenite flow curves in low alloy and microalloyed steels [J]. Acta Materialia, 1996, 44(1): 155-163.

[32] KIM S I, LEE Y, BYON S M. Study on constitutive relation of AISI 4140 steel subject to large strain at elevated temperatures [J]. Journal of Materials Processing Technology, 2003, 140(1-3): 84-89.

[33] JONAS J, SELLARS C M, TEGART W J, MC G. Strength and structure under hot working condition [J]. International Metal Reviews, 1969, 14(130): 1-24.

[34] MILANI A S, DABBOUSSI W, NEMES J A, ABEYARATNE R C. An improved multi-objective identification of Johnson-Cook material parameters [J]. International Journal of Impact Engineering, 2009, 36: 294-302.

一种新型亚稳β钛合金热变形的本构模型

王哲君，强洪夫，王学仁，王 广

西安高新技术研究所，西安 710025

摘  要：基于新型亚稳β钛合金Ti2448在温度1023~1123 K、应变速率63~0.001 s^-1下的等温热压缩流动应力曲线特征，构建能够完整描述该合金流动应力与应变、应变速率、变形温度之间关系的本构模型。在此过程中，通过基于统一黏塑形理论改进双曲正弦函数，构建合金在高应变速率(≥1 s^-1)下发生动态回复(DRV)的模型；通过对标准detrain, 0.01 and 0.1stween flow的Avrami方程进行简化，表征了Ti2448在低应变率(<1 s^-1)下发生的动态再结晶(DRX)软化机制。最终通过应用全局优化求解非线性方程的新方法确定模型中的相关参数。根据所建模型得到的预测曲线和实验曲线吻合得较好，能够有效预测Ti2448在热变形过程中的流动应力，为构建亚稳β钛合金热变形本构模型提供一种有效的方法。

关键词：亚稳β钛合金；热压缩；动态回复；动态再结晶；本构模型

(Edited by YANG Hua)

Corresponding author: WANG Zhe-jun; Tel: +86-13379025436; E-mail: qiulongzaitian@126.com

DOI: 10.1016/S1003-6326(11)61225-9