­ Density functional theory study on hydrogenation mechanism in catalyst-activated Mg(0001) surface

WU Guang-xin(吴广新)¹, LIU Su-xia(刘素霞)¹, ZHANG Jie-yu(张捷宇)¹,

WU Yong-quan(吴永全)¹, LI Qian(李 谦)¹, CHOU Kuo-chi(周国治)^{1, 2}, BAO Xin-hua(包新华)³

1. Shanghai Key Laboratory of Modern Metallurgy and Materials Processing, Shanghai University,

Shanghai 200072, China;

2. Department of Physical Chemistry, University of Science and Technology Beijing, Beijing 100083, China;

3. College of Science, Shanghai University, Shanghai 200444, China

Received 6 October 2008; accepted 10 November 2008

Abstract: A small amount of Fe₃O₄ catalyst is known to substantially improve the adsorption and desorption thermodynamics and kinetics of Mg-based materials. Using density functional theory in combination with nudged elastic band method, the dissociative chemisorptions of hydrogen on both pure and Fe-doped Mg(0001) surfaces were studied. The adsorption energy calculations show that a weakly physisorbed state above pure and Fe-doped Mg surface atoms can serve as a precursor state to dissociative chemisorption. Then, the dissociation pathway of H₂ and the relative barrier were investigated. The calculated dissociation barrier (1.08 eV) of hydrogen molecule on a pure Mg(0001) surface is in good agreement with comparable experimental and theoretical studies. For the Fe-doped Mg(0001) surface, the activated barrier decreases to 0.101 eV due to the strong interaction between the s orbital of H and the d orbital of Fe.

Key words: magnesium alloy; hydrogenation mechanism; catalyst effect; density functional theory

1 Introduction

Magnesium attracts much interest as a possible hydrogen storage material because of its high hydrogen storage capacity (MgH₂ corresponds to 7.6% (mass fraction) hydrogen), non-toxicity and low cost. However, due to kinetic limitations and unmanageable thermodynamic obstacles, pure magnesium is unsuitable as a hydrogen storage material, particularly in the area of mobile applications, where swift hydrogen delivery at low temperatures is at a premium. The low reactivity is mainly attributed to the oxidation of the magnesium surface and limited dissociation rate of hydrogen molecules on this oxidized metal surface. In addition, magnesium metal is difficult to activate and the metal, as well as the magnesium hydride, is very sensitive to contamination[1]. The strong bond between Mg and H provides MgH₂ with high thermodynamic stability, which has an enthalpy of formation of about -76 kJ/mol and a decomposition temperature of more than 300 ℃[2]. The slow kinetics may be explained by the high energy barrier to be overcome[3] to dissociate the H₂ molecule due to the tendency of Mg to repel the s electron of H because of the Pauli exclusion principle[4]. Thus, catalysts are needed so that the storage systems can operate under moderate conditions. In spite of a considerable amount of experimental work studying the role of different catalysts on hydrogen adsorption/ desorption in Mg and MgH₂, no conclusive picture regarding its mechanism has emerged. In this work, we provide such an understanding by carrying out comprehensive theoretical studies of the role of Fe substitution in hydrogen adsorption on the Mg(0001) surface.

Recently, the hydrogen storage properties of the composites composed of Mg or MgH₂ and a small amount of transition metals or transition metal oxides have been studied to improve the hydriding/dehydriding kinetics without reducing its high hydrogen capacity. SHANG et al[5] reported that MgH₂ mixed with Ni gives the highest level of hydrogen desorption and the most rapid kinetics at 300 ℃ under vacuum, followed by alloys with Al, Fe, Nb, Ti, and Cu. And they attributed the kinetic improvements to metal atom substitution. OELERICH et al[6-7] studied the catalytic effects of metal oxides on the hydrogen sorption in nanocrystalline MgH₂. Fe₃O₄ was found to be the best candidate and MgH₂/M_xO_y powders were observed to release hydrogen even at 200 ℃. BARKHORDARIAN et al[8-9] compared Fe₃O₄ with other metal oxide catalysts including Nb₂O₅. Their results demonstrated that the catalytic effects of Fe₃O₄ and Nb₂O₅ are superior in absorption as well as desorption.

Theoretically, JACOBSON et al[10] have used spin-polarized electron-density calculations to determine the diffusion of H on Mg(0001) from surface to bulk with a barrier of 0.5 eV. VEGGE et al[11] investigated the dissociation of H₂ and diffusion of H on the Mg(0001) surface in detail, and found that the favorable dissociation site is the bridge site with a higher active energy of 1.15 eV which is obviously higher than the previous results. And the barrier for H diffusion from surface to bulk is 0.53 eV. The difference with the result of N?RSKOV is that physical adsorption but not chemisorption of molecular hydrogen was observed in the calculation of the dissociation process of molecular hydrogen. In our previous study of H₂ dissociation and diffusion on the Mg(0001) surface[12], we also found that the active barrier for the H₂ dissociation is about 1.05 eV. And the H atoms diffuse slowly to the first subsurface from the surface because of surface effects, while further diffusion to the subsurface is fast to the stable diffusion states. DU et al[13-14] used density functional theory (DFT) to calculate both the pure Mg(0001) and Ti-doped Mg surfaces. Their results showed that the dissociation barrier of hydrogen on the Ti-doped Mg surface is greatly reduced (in fact, there is no barrier at all), due to the strong interaction between the hydrogen s orbital and the Ti d orbital. However, strong binding of the two H atoms near the Ti site prevents easy diffusion, therefore, reducing the efficacy of the catalyst for Mg hydrogenation.

From the study mentioned above, it is not difficult to find that there is no published theoretical investigation of H₂ dissociation and corresponding activation barrier on a Fe-doped Mg(0001) surface. It is well known that dissociative or molecular path is one of important approaches for increasing hydrogen stored amount per unit mass in Mg-based materials. In order to illustrate this question, a better knowledge of the structures and stresses including the physical adsorption, chemical adsorption and diffusion processes is in turn required. In the present work, we report the results of density functional theory calculations within the pseudopotential approximation. This study should be regarded as a first step in order to build up a global picture of the dissociative chemisorption of hydrogen when doping the Mg surface with different transition metals.

2 Method

In this study, we utilized the Vienna ab initio Simulation Package(VASP), which was developed at the University of Vienna by KRESSE and co-workers[15]. In the process of solving the Schr?dinger equation, the generalized gradient approximation(GGA) through the Perdew-Wang 91 (PW91)[16] function and projector augmented wave(PAW)[17] were employed for all calculations to describe the exchange-correction energy and the computationally expensive electron-ion interaction, respectively. A plane-wave basis set was used for the expansion of the single particle Kohn-Sham wavefunctions. Sampling of the irreducible wedge of the Brillouin zone was performed with a regular Monkhorst- Pack grid of special k-points[18]. Ground state atomic geometries were obtained by minimizing the Hellman- Feynman(H-F) forces using a conjugate gradient algorithm[19]. Atomic relaxations were achieved by using the calculated H-F forces as a guide in the processes of the adjustment of the atomic configurations until the H-F force on each atom was less than 0.05 eV/nm. The calculation was performed in the Fast-Fourier-Transform grids.

We used a periodic six-layer Mg slab (1.3 nm) with clean surface and adatoms adsorbed on one side of the slab. Periodic boundary conditions were used, with the one electron pseudo-orbitals expanded over a plane wave basis set. For the purpose of reducing the adulterate concentration of Fe, we used a (3×3) surface model. Meanwhile, in order to compare with the pure model, we recalculated the Mg(0001) (3×3) surface unit cell (see Fig.1(b)). The corresponding kinetic energy cutoffs were 400 eV for PAW calculations. Brillouin-zone integrations employed a 5×5×1 Monkhorst-Pack grid of k-points for all the supercells. The slab was separated from its periodic image in the direction normal to the surface by a vacuum space of more than 2.0 nm. Slab calculations allowed three surface layers to relax, holding the bottom layers fixed in their optimized bulk positions.

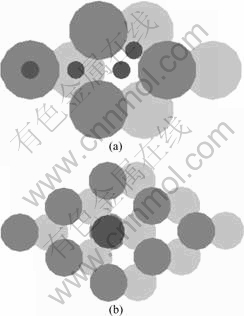
Fig.1 Computation model used in this work: (a) Adsorption sites (Jet black ball) of Mg(0001) surface: (left to right) top, hcp, fcc, and bridge site; (b) Fe-doped Mg(0001) surface model (Jet black ball represents Fe atom)

An improved version of the nudged elastic band (NEB) method, the climbing-image NEB[20], was used to locate the minimum energy pathways(MEP) and the transition states(TS) for the dissociation and diffusion of H on pure and Fe-doped Mg surface. When we used the climbing-image-NEB(CI-NEB) method in this study, all the images were relaxed until the maximum force acting on an atom is less than 0.1 eV/nm. A smaller set of k-points (5×5×1) and a lower energy cutoff (300 eV) were used for NEB calculations due to their computational expense. When the energy difference between the initial state and transition state on the clean surface was recomputed using more k-points (7×7×1) and a higher cutoff energy (400 eV), the activation barrier only differed from our original NEB result by 0.1 eV.

3 Results and discussion

3.1 Bulk Mg and H₂ molecular

In order to determine the equilibrium bulk parameters of Mg, we uniformly scaled the lattice vectors and calculated the energy as function of the unit cell volume. The data were then fitted to the Birch-Murnaghan equation of state[21], which predicted lattice constants of a=0.319 nm and c/a=1.62. These values are in good agreement with the corresponding experimental values of a=0.321 nm and c/a=1.624[22]. The cohesive energy was calculated as a difference between the total energy per atom in a bulk crystal and the total energy of a free atom. The latter was determined for a single atom in a cubic cell of box length about 1.0 nm that was big enough to avoid interactions with atoms from the neighbouring cells. The calculated result is E_coh=-1.48 eV/atom, which is in good agreement with the corresponding experimental value of E_coh=-1.51 eV/atom[23]. Then the test we performed was related to predictions of equilibrium properties of H₂ molecule in gas phase. In this case, an isolated H₂ molecule was optimized in a cubic box of 1.0 nm. The bond length and bond energy of molecular hydrogen calculated from our DFT approach are r_H—H=0.075 nm and E_Binding=4.55 eV without zero point energy correction, in good agreement with the experimental values of 0.074 nm[24] and 4.52 eV[25], respectively. These values indicate that the present set of pseudopotentials, as well as the k-points mesh and the cutoff energy, is able to provide a very good representation of the structural properties of bulk Mg and H₂.

3.2 Hydrogen adsorption on pure and Fe-doped Mg surface

Next, in order to prepare the input configurations for the NEB calculation, we calculated the adsorption energies for the molecular and atomic hydrogen. The adsorption energies for molecular and atomic hydrogen are defined as

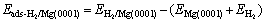   (1)

and

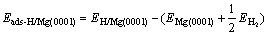   (2)

where 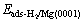 and E_{ads-H/Mg(0001)} are the adsorp- tion energy of systems with adsorbed H₂ molecule and H atom, respectively;  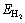is the total energy of a H₂ molecule in the gas phase; E_Mg(0001) is the total energy of the Mg slab without adsorbed species; and  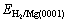and E_H/Mg(0001) are the total energies of systems with adsorbed H₂ molecule and H atom, respectively. With this definition, negative values of adsorption energy denote adsorption that is more stable than the corresponding clean surface and gas phase H₂. The calculated adsorption energies reported in this study do not include zero point energy corrections.

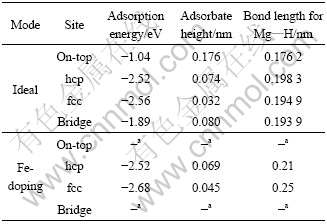
For this molecular adsorption configuration, the corresponding binding energy calculated based on Eq.(1) is small with a value of 0.03 eV, which indicates the a weakly physisorbed state occurred even for the Fe-doped Mg surface (see Table 1). However, it is well-known that DFT cannot give reliable energies for weakly bound systems. Therefore, the absolute energies for these physisorbed molecules are not likely to be accurate. This is not a severe difficulty for our purposes, since a change in these physisorption energies will not have a large effect on the quantity of interest to us, namely the dissociation barrier.

Table 1 Adsorption energy, adsorbate height and bond length for different adsorption sites considered for H₂ molecule on different surfaces

The calculated adsorption energies for atomic H on Mg(0001) surface with different sites (see Fig.1(a)) are presented in Table 2. It is also an examination of adsorption of H atom in order to identify the initial state for H atom diffusion. For the pure Mg surface, the fcc position is found to be a preferred site for adsorption which is 40 meV higher than the binding energy of hcp position. For the Fe-doped Mg surface, although it should be emphasized that adsorption in the bridge and top sites appears to be unstable, the fcc site is also the minimum energy position.

Table 2 Adsorption energy, adsorbate height and bond length for different adsorption sites considered for H atom on different surfaces

3.3 H₂ dissociation on pure and Fe-doped Mg surface

We now discuss the dissociation pathways for H₂ dissociation on the Mg surfaces. Firstly we investigated the H₂ dissociation on the ideal Mg(0001) surface. The minimum energy pathway (MEP) of the hydrogen molecule dissociation on the surface of pure Mg(0001) layer is displayed in Fig.2(a). The energy of the initial-state structure is set as zero. It is clear that the dissociation of hydrogen molecule on the pure Mg(0001) layer is exothermic with a value of 84 meV, which agrees well with EELS spectra from Sprunger and Plummer, having an energy loss of 92 meV[3, 26]. Following the reaction coordinate, the transition state for the dissociation is found to be in the bridge site with a longer bond length of 0.116 nm, which is in agreement with the theoretical and experimental results[11, 13, 27]. A higher dissociation activation barrier of 1.08 eV is found, which is consistent with the results of VEGGE [11] (1.15 eV) and DU et al[13] (1.05 eV), but much higher than the calculated results by NORSKOV et al  [28] of 0.5 eV and the experimental result (0.6-0.9 eV)[27]. The difference can be explained by the presence of step sites which have a lower barrier for dissociation than terrace sites. Such effects have been observed for several diatomic dissociation reactions[29].

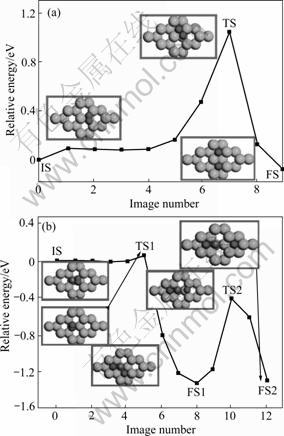
Fig.2 Different minimum energy pathways for H₂ molecular dissociation on Mg(0001) surface: (a) Pure model; (b) Fe-doped model (All NEB processes are constructed with an initial state (IS) consisting of H₂ molecular on pure and Fe-doped Mg(0001) surface and final state(FS) consisting of two H atoms on surface. Large grayish, smaller gray and smallest jet black balls represent Mg, Fe and H atoms, respectively.)

Having benchmarked our calculations on the pure Mg surfaces, we now come to the main purpose of the paper, which is to study the effect of Fe doping on the Mg(0001) surface for the activation barriers of H₂ dissociation, and diffusion on the surface and in the bulk.

On the Mg(0001) surface, we found that Fe is nonmagnetic. So, all calculations were performed without including spin polarization. Fig.2(b) shows the dissociation process of the hydrogen molecule over the Fe atom as viewed at the IS, TS1 and FS1 states. It should be noted that on the Fe-doped Mg surface, the molecule at the TS1 is much higher than that on the pure Mg (0001) surface (Table 2), being at 0.077 nm over the surfaces. For the NEB calculations, we found that 13 replicas are enough for a precise calculation of the energy barrier within the range of 0.1 eV. The resulting activation barrier for H₂ dissociation on a Fe incorporated Mg surface is 0.101 eV, against 1.08 eV for the pure Mg surface. This barrier is similar to the value found on the Ti-doped surface by DU et al[14], and Ni-doped surface by POZZO et al[30] with an energy barrier of 0.103 eV and 0.06 eV, respectively. This suggests that in the transition elements group, Ni should be an even better catalyst than Fe and Ti for the hydrogenation of Mg, which agrees well with SHANG et al’s experiment result[5].

With the energetics of the H₂ dissociation process on the Fe-doped Mg(0001) surface obtained, we continue to study the atomic H diffusion over the Fe on the surface. The calculated diffusion pathway is plotted in Fig.2(b) (viewed at the FS1, TS2, and FS2). The activation energy from the FS1 site to the FS site is 0.937 eV, which is higher than our results for pure Mg surface with a value of 0.21 eV[12]. And the energy difference between the FS1 and FS2 sites is found to be 52 meV, while the obtained relative value for pure model is 30 meV[12] and 20 meV[10]. And we noticed that in FS1 site the two hydrogen atoms surround the Fe atom while in FS2 site one of hydrogen is far from Fe atom. This suggests that the dopant-Fe has a stronger attraction than Mg to make hydrogen tightly shrunk.

To study the electronic properties of the system, we projected the electronic density of states(DOS) onto spherical harmonic functions of type s, p and d, centered on Mg, Fe and H atoms. Fig.3 represents the projected density of states(PDOS) calculated for the pure Mg and Fe-doped Mg surfaces, respectively. The PDOSs are given for a number of configurations along the MEP: the IS, the TS and the FS. In the IS, the hydrogen molecule is still far from the metal surface and there is no overlap between the orbitals of H₂ molecular and the orbitals of metal surface. At the transition state, instead, when gaseous hydrogen starts dissociating over the surface, there is clear interaction between the H s orbital and the Mg s and p orbitals on the pure Mg surface (see  Fig.3(b)). On the Fe-doped surface, the overlap appears to be nonzero with all the Fe s, p and d orbitals and H s orbital (see Fig.3(e)). In the final state, it is evident that the magnitude of Mg p electron peaks below the Fermi level is increased in the Fe-doped surfaces (see Fig.3(f)) with respect to the pure Mg surface (see Fig.3(c)). This means that the stronger interaction between the s orbital of H and the d orbital of Fe leads to the activation barrier of surface diffusion for H₂ on the Fe-doped model apparently higher than that on the pure model.

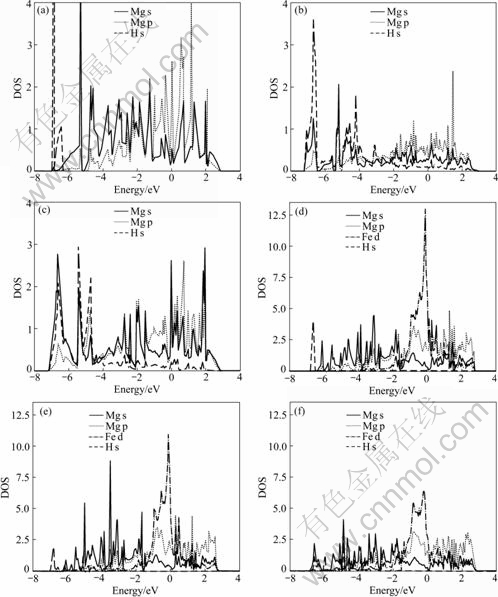
Fig.3 Projected densities of states for H₂ dissociating over Mg surface as function of energy relative to Fermi level: IS (a), TS (b) and FS (c) of pure model, respectively; IS (d), TS (e) and FS (f) of Fe-doped model, respectively

4 Conclusions

1) Adsorption energy calculations show that a weakly physisorbed state above pure and Fe-doped Mg surface atoms can serve as a precursor state to dissociative chemisorption.

2) The energy barrier for hydrogen dissociation is high on the pure Mg surface (1.08 eV) and it is small (0.101 eV) when Fe is used as dopant due to the strong interaction between the molecular orbital of hydrogen and the d metal state of Fe.

References

[1] LEON A, KNYSTAUTAS E J, HUOT J, SCHULZ R. Hydrogenation characteristics of air-exposed magnesium films [J]. J Alloys Compds, 2002, 345(1/2): 158-166.

[2] BOGDANOVIC B, BOHMHAMMEL K, CHRIST B, REISER A, SCHLICHTE K, VEHLEN R, WOLF U. Thermodynamic investigation of the magnesium-hydrogen system [J]. J Alloys Compds, 1999, 282(1/2): 84-92.

[3] SPRUNGER P T, PLUMMER E W. An experimental study of the interaction of hydrogen with the Mg(0001) surface [J]. Chem Phys Lett, 1991, 187(6): 559-564.

[4] HAMMER B, NORSKOV J K. Electronic factors determining the reactivity of metal surfaces [J]. Surf Sci, 1995, 343(3): 211-220.

[5] SHANG C X, BOUOUDINA M, SONG Y, GUO Z X. Mechanical alloying and electronic simulations of (MgH₂+M) systems (M=Al, Ti, Fe, Ni, Cu and Nb) for hydrogen storage [J]. Int J Hydrogen Energy, 2004, 29(1): 73-80.

[6] OELERICH W, KLASSEN T, BORMANN R. Comparison of the catalytic effects of V, V₂O₅, VN, and VC on the hydrogen sorption of nanocrystalline Mg [J]. J Alloys Compds, 2001, 322(1/2): L5-L9.

[7] OELERICH W, KLASSEN T, BORMANN R, UUML, DIGER. Mg-based hydrogen storage materials with improved hydrogen sorption [J]. Mater Trans, 2001, 42(8): 1588-1592.

[8] BARKHORDARIAN G, KLASSEN T, BORMANN R. Fast hydrogen sorption kinetics of nanocrystalline Mg using Nb₂O₅ as catalyst [J]. Scripta Mater, 2003, 49(3): 213-217.

[9] BARKHORDARIAN G, KLASSEN T, BORMANN R. Effect of Nb₂O₅ content on hydrogen reaction kinetics of Mg [J]. J Alloys Compds, 2004, 364(1/2): 242-246.

[10] JACOBSON N, TEGNER B, SCHRODER E, HYLDGAARD P, LUNDQVIST B I. Hydrogen dynamics in magnesium and graphite [J]. Comput Mater Sci, 2002, 24(1/2): 273-277.

[11] VEGGE T. Locating the rate-limiting step for the interaction of hydrogen with Mg(0001) using density-functional theory calculations and rate theory [J]. Phys Rev B, 2004, 70(3): 035412-035419.

[12] WU G X, ZHANG J Y, WU Y Q, LI Q, CHOU K C, BAO X H. First-principle calculations of the adsorption, dissociation and diffusion of hydrogen on the Mg(0001) surface [J]. Acta Physico-Chimica Sinica, 2008, 24(1): 55-60.

[13] DU A J, SMITH S C, YAO X D, LU G Q. The role of Ti as a catalyst for the dissociation of hydrogen on a Mg(0001) surface [J]. J Phys Chem B, 2005, 109(38): 18037-18041.

[14] DU A J, SMITH S C, YAO X D, LU G Q. Hydrogen spillover mechanism on a Pd-doped Mg surface as revealed by ab initio density functional calculation [J]. J Am Chem Soc, 2007, 129(33): 10201-10204.

[15] KRESSE G, FURTHMULLER J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set [J]. Phys Rev B, 1996, 54(16): 11169-11186.

[16] PERDEW J P, CHEVARY J A, VOSKO S H, JACKSON K A, PEDERSON M R, SINGH D J, FIOLHAIS C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation [J]. Phys Rev B, 1992, 46(11): 6671-6687.

[17] BLOCHL P E. Projector augmented-wave method [J]. Phys Rev B, 1994, 50(24): 17953-17979.

[18] MONKHORST H J, PACK J D. Special points for Brillouin-zone integrations [J]. Phys Rev B, 1976, 13(12): 5188-5192.

[19] PRESS W H, TEUKOLSKY S A, VETTERLING W T. Numerical recipes in Fortran 90: The art of parallel scientific computing [M]. New York: Cambridge University Press, 1996.

[20] HENKELMAN G, UBERUAGA B P, JONSSON H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths [J]. J Chem Phys, 2000, 113(22): 9901-9904.

[21] BIRCH F. Finite elastic strain of cubic crystals [J]. Phys Rev, 1947, 71(11): 809-824.

[22] LI X G, ZHANG P, CHAN C K. First-principles calculation of Mg(0 0 0 1) thin films: Quantum size effect and adsorption of atomic hydrogen [J]. Phys B: Condens Matter, 2007, 390(1/2): 225-230.

[23] ASHCROFT N W, MERMIN N D. Solid state physics [M]. New York: Holt, Rinehart and Winston, 1976.

[24] SUTTON L E. Table of interatomic distances and configuration in molecules and ions [M]. London: Chemical Society, 1965.

[25] KERR J A. Handbook of chemistry and physics [M]. Boca Raton, Florida: CRC Press, 2000.

[26] SPRUNGER P T, PLUMMER E W. The interaction of hydrogen with simple metal surfaces [J]. Surf Sci, 1994, 307/309(Part 1): 118-123.

[27] JOHANSSON M, OSTENFELD C W, CHORKENDORFF I. Adsorption of hydrogen on clean and modified magnesium films [J]. Phys Rev B, 2006, 74(19): 193408-193404.

[28] NORSKOV J K, HOUMOLLER A, JOHANSSON P K, LUNDQVIST B I. Adsorption and dissociation of H₂ on Mg surfaces [J]. Phys Rev Lett, 1981, 46(4): 257-260.

[29] DAHL S, LOGADOTTIR A, EGEBERG R C, LARSEN J H, CHORKENDORFF I, TORNQVIST E, NORSKOV J K. Role of steps in N₂ activation on Ru(0001) [J]. Phys Rev Lett, 1999, 83(9): 1814-1817.

[30] POZZO M, ALFE D, AMIEIRO A, FRENCH S, PRATT A. Hydrogen dissociation and diffusion on Ni- and Ti-doped Mg(0001) surfaces [J]. J Chem Phys, 2008, 128(9): 094703-094711.

(Edited by YUAN Sai-qian)