基于差分遗传算法的置换流水车间低碳调度模型
杨海东1,郑庆仁2,刘国胜3,郭建华4
(1. 广东工业大学 机电工程学院,广东 广州,510006;
2. 华南理工大学 自动化科学与工程学院,广东 广州,510641;
3. 广东工业大学 信息管理工程系,广东 广州,510520;
4. 广东技术师范学院 计算机科学学院,广东 广州,510665)
摘要:研究置换流水车间(permutation flow shop,PFS)中的能效优化问题,考虑串行生产线中机器功率、空闲时间等因素对能源消耗的影响,建立以高效低碳为目标的PFS模型。给出问题的数学规划形式,并采用遗传算法对其求解,所给出的遗传算法通过启发式规则、随机规则和翻转规则产生初始种群,根据任务的能耗差分来计算种群中个体的进化概率和进化方向,同时提出非等长LOX交叉算子。对华南地区某大型轮胎制造企业进行实例分析,研究结果表明:所采用的改进策略可提高遗传算法整体性能50%以上;采用文中模型和方法可降低轮胎生产过程能耗8%左右。
关键词:置换流水车间;能效优化;遗传算法;差分策略;轮胎生产
中图分类号:TP273 文献标志码:A 文章编号:1672-7207(2013)11-4554-07
Low-carbon scheduling in permutation flow shop problem by differential genetic algorithm
YANG Haidong1, ZHENG Qingren2, LIU Guosheng3, GUO Jianhua4
(1. School of Mechatronics Engineering, Guangdong University of Technology, Guangzhou 510006, China;
2. School of Automation Science & Engineer, South China University of Technology, Guangzhou 510641, China;
3. Department of Information Management Engineering, Guangdong University of Technology, Guangzhou 510520, China;
4. School of Computer Science, Guangdong Polytechnic Normal University, Guangzhou 510665, China)
Abstract: The energy-efficient optimization in permutation flow shop (PFS) was investigated. A novel high-efficiency low-carbon model was proposed in which effects of machine power consumption and idle time were considered on energy consumption. The problem was formulated by mathematical programming and solved by genetic algorithm (GA). Adopting heuristic rule, random rule, and reverse rule to generate the initial population, and determining the evolution direction and probability according to the difference of energy consumption, an unequal LOX crossover operation was also adopted. A case study for a tire manufacturing company located in South China was made. The results show that the proposed scheme improves the performance of GA at least 50%. The proposed method can reduce approximately 8% energy consumption in tire manufacturing process.
Key words: permutation flow shop (PFS); energy-efficient optimization; genetic algorithm; differential scheme; tire manufacturing
随着人们对全球气候变暖问题的关注和能源价格的不断上涨,制造业承受着越来越多的成本压力和环保挑战,发展中国家亟需通过产业升级转型改变传统仅注重生产效率的制造模式。在制造过程中,如何降低单位产品能耗成为新的研究热点。调度问题研究通过改变生产线上机器配置和任务加工次序的手段来达到生产目标,其具有广泛适用性和实用性,此类问题一直被众多学者和工程技术人员所研究。然而,已有研究多以生产效率为目标,通过调度优化达到单位时间产量最大化,如最大完成时间、延迟交货时间(数)、加权完成时间等[1-3]。目前,仅有少数学者考虑通过调度优化来实现生产过程中的节能低碳目标。Rahimifard等[4-5]通过分析不同制造过程中的能源消耗类型,将能耗分为直接能耗和间接能耗,建立起一种基本的制造过程能耗模型。Mouzon等[6-7]提出制造设备最小化能耗的操作方法,建立以机器能耗最小和总任务完成时间最短的多目标数学规划模型,并讨论了单机情形中的能耗优化问题。 等[8]提出一种支持生产计划流程替换的调度框架,该框架采用人机结合的方式选择适合的生产计划。Drake等[9]提出一种生产过程中能耗数据收集、处理和评价方法。Fang等[10]考虑生产过程中能量峰值负载、能耗、碳足迹等因素,通过商业软件求解多目标问题的Pareto解向量。在国内,刘向[11]给出了面向节能降耗的生产调度模型,李凯[12]讨论了单机情形中高能耗关键机器下的调度优化问题,印二威[13]研究了铝工业中的节能调度问题。总之,目前对低碳调度问题的研究尚处于摸索阶段,没有完整理论基础和充分实验论证,已有的研究均针对某种具体工艺流程,采用逐步优化的方式进行求解,不能推广到一般制造过程。本文作者从传统置换流水车间(permutation flow shop,PFS)理论模型出发,讨论流水线上机器功率和机器空闲时间与生产能耗的关系,建立一种基本的PFS低碳调度模型,讨论PFS低碳调度模型与传统调度模型的区别,并提出一种采用启发式规则和差分进化操作的遗传算法,最后通过数值实验验证差分遗传算法的有效性,并采用所提出模型和方法对轮胎制造过程中的调度问题进行优化。文中所提出的模型和方法均可推广到其他制造过程中的低碳调度优化问题。
等[8]提出一种支持生产计划流程替换的调度框架,该框架采用人机结合的方式选择适合的生产计划。Drake等[9]提出一种生产过程中能耗数据收集、处理和评价方法。Fang等[10]考虑生产过程中能量峰值负载、能耗、碳足迹等因素,通过商业软件求解多目标问题的Pareto解向量。在国内,刘向[11]给出了面向节能降耗的生产调度模型,李凯[12]讨论了单机情形中高能耗关键机器下的调度优化问题,印二威[13]研究了铝工业中的节能调度问题。总之,目前对低碳调度问题的研究尚处于摸索阶段,没有完整理论基础和充分实验论证,已有的研究均针对某种具体工艺流程,采用逐步优化的方式进行求解,不能推广到一般制造过程。本文作者从传统置换流水车间(permutation flow shop,PFS)理论模型出发,讨论流水线上机器功率和机器空闲时间与生产能耗的关系,建立一种基本的PFS低碳调度模型,讨论PFS低碳调度模型与传统调度模型的区别,并提出一种采用启发式规则和差分进化操作的遗传算法,最后通过数值实验验证差分遗传算法的有效性,并采用所提出模型和方法对轮胎制造过程中的调度问题进行优化。文中所提出的模型和方法均可推广到其他制造过程中的低碳调度优化问题。
1 流水车间低碳调度模型
PFS问题研究多个任务在单条流水生产线上的最优加工次序,通常假设所有任务具有相同的开始时间,生产线上每台机器同一时间最多只能处理1个任务,加工过程不可中断[1, 14]。PFS问题的低碳调度模型相关符号如表1所示。
表1 相关符号说明
Table 1 Instruction of related symbols
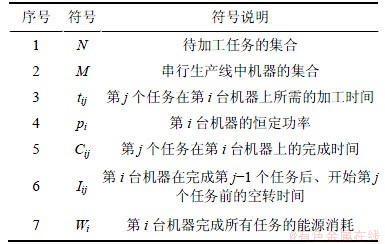
另外,假设机器在空闲等待过程中不停机,将以高效低碳为目标的PFS模型记为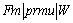 ,其数学表达式为:
,其数学表达式为:
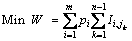 (1)
(1)
st.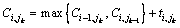
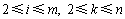 (2)
(2)
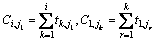 (3)
(3)
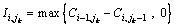 ,
,
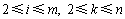 (4)
(4)
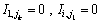 (5)
(5)
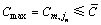 (6)
(6)
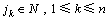 (7)
(7)
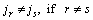 (8)
(8)
式(7)和(8)为PFS问题的基本约束,表示任务不可中断和机器不可被抢占。式(2)~(5)为PFS问题中计算任务完成时间和机器空闲时间的表达式,可以看出:第1台机器可连续工作,而第1个任务可依次被加工而无需等待。式(6)表示生产效率的约束,其中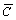 为任务的规定完成时间。
为任务的规定完成时间。
若流水线上最后一台机器为关键机器,即
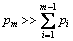 ,则目标函数可等价为
,则目标函数可等价为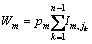 ,可得到关系式:
,可得到关系式:
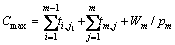 (9)
(9)
式中:右边第1项仅与第1个位置的任务(j1)有关,第2项是常量。因此,通过选择不同的任务放置于初始位置,优化问题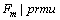 ,
,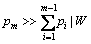 可转化为n个
可转化为n个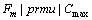 问题来求解。这也说明:
问题来求解。这也说明: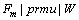 具有不低于
具有不低于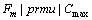 的计算复杂度。下面通过遗传算法寻找此模型最优排序
的计算复杂度。下面通过遗传算法寻找此模型最优排序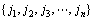 ,使得在给定时间内以最小能源消耗来完成生产任务。
,使得在给定时间内以最小能源消耗来完成生产任务。
2 差分遗传算法求解过程
由于此类调度问题是NP-hard问题,采用遗传算法求解此类问题是一种行之有效的方法[14-16]。本文采用一种基于差分策略的遗传算法(differential genetic algorithm,DGA)来求解PFS低碳调度模型。
2.1 初始种群
初始种群决定了种群进化的初始状态,它会对算法的搜索路径和收敛速度产生影响。通常种群中个体的初始位置既要与最优解位置尽量靠近,又要尽量均匀分布于解空间。本文采用与文献[13]中相同的策略,通过启发式规则、随机规则和翻转规则来共同产生初始种群。其中启发式规则采用高能耗任务优先的规则,并通过改变起始任务来进行扩充。算法中所用到的规则说明如下。
LPT:按照理论能耗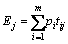 对所有任务进行降序排列,即能耗高的任务应优先加工。
对所有任务进行降序排列,即能耗高的任务应优先加工。
SLPT:对由LPT规则产生的序列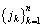 通过交
通过交
换j1与jk的位置得到新个体, 此方法可得到n-1个新个体。
RV:对由LPT和SLPT产生的序列进行反转操作得到新个体,此方法可产生同等数量的新个体。
RA:通过随机方法产生新个体,新个体数量按种群规模与已有个体数量的差值来确定。
2.2 选择算子
选择算子在解空间中以一定概率选择优良个体进行遗传操作,然而,PFS低碳调度模型中存在对完成时间的不等式约束(见式(6)),可能造成解空间中存在孤立区域,隔断算法搜索路径。为此,将其中的不等式约束以惩罚项的形式加入目标函数中,提高算法搜索能力。每个个体的适应度按下式计算:
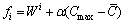 (10)
(10)
其中: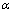 为所有机器的平均功率;上标i表示第i个个体,则第i个个体被选择的概率为
为所有机器的平均功率;上标i表示第i个个体,则第i个个体被选择的概率为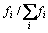 。
。
2.3 交叉算子
在进行交叉时,子代个体应能尽量保留父本中的优良片段,选择合适的交叉点位置才能确保种群的进化方向。在基因片段(j1, j2, j3, …, jk)中,定义其能耗差分为:
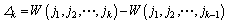 ,
,
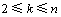 (11)
(11)
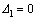 (12)
(12)
则交叉点的位置由最大差分点确定:
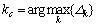 (13)
(13)
在确定交叉点后,采用LOX方式对父本进行交叉操作[14]。传统LOX方式是针对相同长度的基因片段设计的,但为了更好地保留父本的优良基因,本文将其扩展到非等长基因片段的情况,以适应以上由最大能耗差分来确定的交叉操作。例如:对于待交叉的2个父本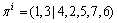 ,
,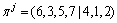 。假设根据最大能耗差分确定的交叉点
。假设根据最大能耗差分确定的交叉点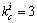 和
和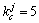 ,则通过LOX方式进行交叉变换得到的新个体分别为:
,则通过LOX方式进行交叉变换得到的新个体分别为: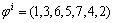 ,
,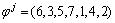 。
。
2.4 变异算子
遗传算法除了要保证种群往适应值高的方向进化外,还需使种群具有全局搜索能力。在本文的遗传算法中,采用随机方式进行变异操作。另外,可以观察到应用于调度问题的交叉算子[14]均不会改变第1个位置的任务(j1的取值),这种现象会在解空间中形成搜索盲区。为避免盲区的出现,本文首先随机生成一个变异点km:
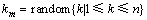 (14)
(14)
通过交换j1与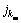 产生一个新的变异子个体。
产生一个新的变异子个体。
3 数值实验
3.1 算法性能比较
将本文算法与传统随机遗传算法(randomly genetic algorithm, RGA)的比较,实验采用标准数据集TA进行验证,TA标准数据集提供了12组不同规模的PFS问题,每组问题含10个数据集,每个任务处理时间均为1~100之间的随机整数[17]。本文选取每组问题中的第1个数据进行实验,实验中选取交叉概率Pc=0.8,变异概率Pm=0.1。由于实验中采用轮盘赌的方式选择交叉个体和变异个体,对每个问题重复试验100次,比较2种算法目标函数的平均值(MEA)、标准差(STDEV)和优胜率。其中优胜率定义如下:
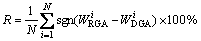 (15)
(15)
其中,R为优胜率;N为试验次数;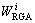 和
和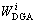 分别为采用RGA方法和DGA方法时的能耗。
分别为采用RGA方法和DGA方法时的能耗。
表2所示为2种算法所得到的12个问题的能源消耗对比结果。从表2可以看出:采用DGA方法计算的目标函数值均优于RGA方法,且目标值分布更加集中。经过统计发现:本文中所给出的DGA方法相对于RGA方法的优胜率均在50%以上,最高达到78%,算法性能得到极大提高。
3.2 模型能效分析
当流水线上最后一台机器为关键机器时,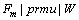 转化为多个传统的
转化为多个传统的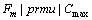 问题,因此,低碳调度模型与传统最小化完成时间模型具有某种程度的一致性。但这里将通过数值实验验证本文所给出模型对置换流水车间低碳运行产生显著的优化效果。选取TA数据集中规模为m=10,n=50的10个数据集(TA041~TA050)作为实验数据,采用DGA算法分别以能耗最低(Min W)和完成时间最小(Min Cmax)对10个问题进行求解。图1所示为2种模型中由机器空转所产生的能源消耗的对比结果。从图1可以看到:新模型可有效降低生产过程中的机器空转能耗,平均能耗降低率为50.45%,新模型极大提高了机器整体利用率。图2所示为2种模型完成时间对比。从图2可以看出:新模型在有效降低生产过程中的机器空转能耗的同时也增加了产品完成时间,不过其平均增加量为6.25%,而相对于其能耗降低量来说,新方法对完成时间的影响非常小。图3所示为用DGA算法求解2种模型在TA041数据集中的收敛情况。在进行50次迭代的过程中,本文所给出的模型对以能耗为目标的PFS问题具有良好收敛效果。
问题,因此,低碳调度模型与传统最小化完成时间模型具有某种程度的一致性。但这里将通过数值实验验证本文所给出模型对置换流水车间低碳运行产生显著的优化效果。选取TA数据集中规模为m=10,n=50的10个数据集(TA041~TA050)作为实验数据,采用DGA算法分别以能耗最低(Min W)和完成时间最小(Min Cmax)对10个问题进行求解。图1所示为2种模型中由机器空转所产生的能源消耗的对比结果。从图1可以看到:新模型可有效降低生产过程中的机器空转能耗,平均能耗降低率为50.45%,新模型极大提高了机器整体利用率。图2所示为2种模型完成时间对比。从图2可以看出:新模型在有效降低生产过程中的机器空转能耗的同时也增加了产品完成时间,不过其平均增加量为6.25%,而相对于其能耗降低量来说,新方法对完成时间的影响非常小。图3所示为用DGA算法求解2种模型在TA041数据集中的收敛情况。在进行50次迭代的过程中,本文所给出的模型对以能耗为目标的PFS问题具有良好收敛效果。
3.3 轮胎生产中的低碳调度优化
以华南地区某大型橡胶轮胎制造企业为例,挖掘轮胎生产过程中通过调度方法可达到的节能潜力。图4所示为轮胎生产过程的4道关键耗能工序。其中,炼胶采用的是目前较常用的两段炼胶法,因此,需分为2个独立的子工序,其主要作用是将轮胎原料通过初加工形成混炼胶。压延是将混炼胶制成具有特定形状和尺寸的胶片、胶条、胎面胶、胶帘布及胶帆布等,制造出生产轮胎所需要的各种半成品。压延工艺采用压延联动装置,同时包含钢丝帘布裁断过程。成型是将各种轮胎半成品通过成型机的贴合,得到半成品胚胎的过程。硫化是轮胎制造的最后一道工序,指在一定的压力和温度条件下,通过硫化方法改变橡胶的化学结构,从而制成具有特殊硬度、弹性的轮胎成品的过程。
表2 算法性能比较结果
Table2 Comparison results of algorithms performance
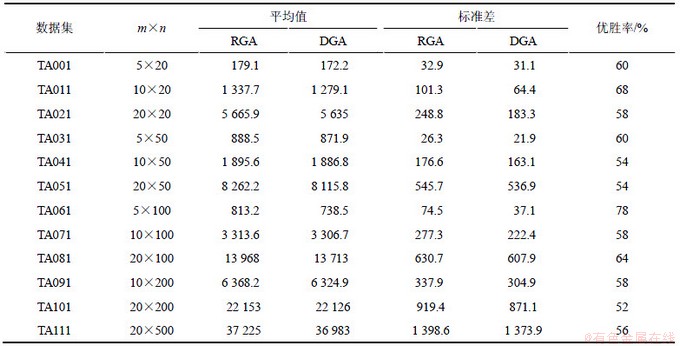
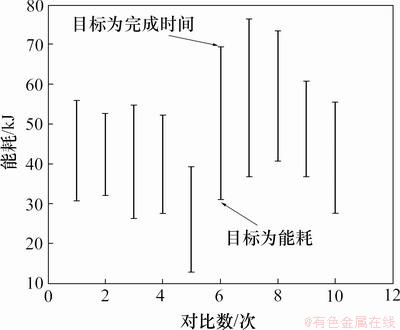
图1 2种目标下的空转能耗情况对比
Fig.1 Comparison of idling energy consumption under two kinds of targets
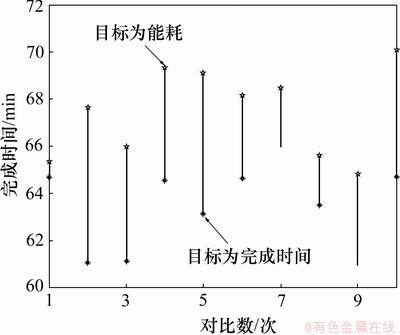
图2 2种目标下的完成时间情况对比
Fig.2 Comparison of completion time under two kinds of targets
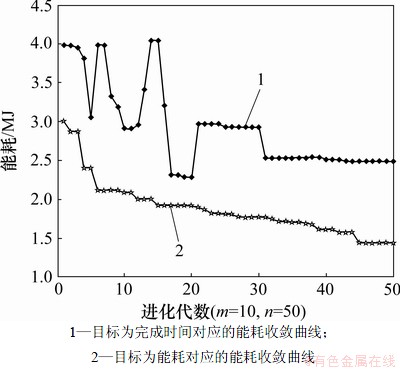
图3 2种目标下的算法收敛情况对比(TA41数据集)
Fig.3 Comparison of algorithm convergence under two kinds of targets (TA041 data set )
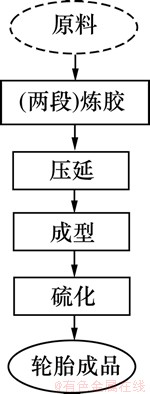
图4 轮胎加工工艺过程
Fig.4 Tire manufacturing process
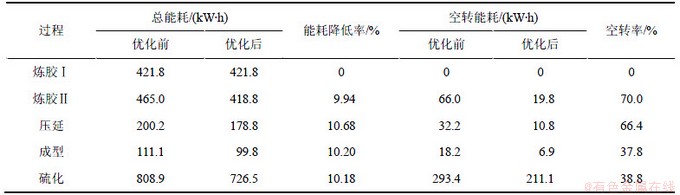
从公司生产管理系统和能源管理系统中调出连续8批订单的生产记录,同批型号的产品加工时间见表3,其中订单任务按照历史加工顺序进行编号,假设每批订单包含10件产品。公司中某条生产线上5个关键工序的能耗见表4。采用DGA算法对这批产品进行重新调度排序,种群规模选为500,经过多次验证,选取交叉概率Pc=0.75,变异概率Pm=0.2,算法经过100次迭代计算后停止。经过优化后的能耗结果如表4所示,其中优化前采用的是顺序加工方式。由于第1道工序中的机器可连续工作,因此不会因空闲产生能源消耗。从表4可知:通过低碳调度后总能耗可降低约8.04%,机器空转率可下降至39.4%。
表3 轮胎产品生产工艺参数
Table 3 Tire production process parameters
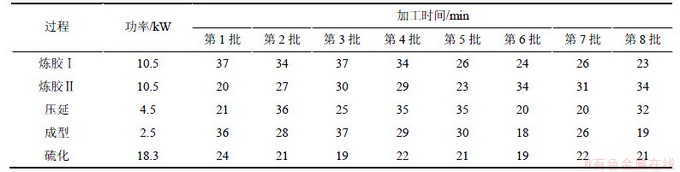
表4 轮胎生产节能潜力挖掘
Table 4 Exploitation of energy saving potentialities in tire production
4 结论
(1) 针对PFS问题提出一种新的低碳调度模型,模型以最小化生产能耗为目标,建立了基于流水车间中机器功率和空转时间的目标函数,区别于传统以任务完成时间为目标的调度模型。
(2) 此模型在提高PFS问题的能效方面有显著效果,平均可降低单位产品能源消耗8%左右。
(3) 针对所给出模型提出基于差分策略的遗传算法,此方法可提高算法搜索效率50%以上,并可同时推广到其他PFS问题中。
(4) 本文的研究内容和结论将推动绿色制造领域通过调度方法实现高效低碳的生产目标,为高能耗企业实现节能减排提供科学可行的途径。
参考文献:
[1] Potts C N, Strusevich V A. Fifty years of scheduling: A survey of milestones[J]. Journal of the Operational Research Society, 2009, 60(1): S41-S68.
[2] 王晶, 王伟玲. 具有交货时间窗约束的无等待流水车间调度模型与算法[J]. 中国机械工程, 2010, 21(19): 2334-2344.
WANG Jing, WANG Weiling. Model and algorithm for no-wait flow shop scheduling problem based on delivery time constraint[J]. Mechanical Engineering, 2010, 21(19): 2334-2344.
[3] LIAO Xiaoping, LIU Yougen, LI Xiaoping. Hybrid evolutionary algorithm for no-wait flow shops to minimize makespan and total flow time[J]. Journal of Southeast University: English Edition, 2008, 24(4): 450-454.
[4] Rahimifard S, Seow Y, Childs T. Minimising embodied product energy to support energy efficient manufacturing[J]. CIRP Annals-Manufacturing Technology, 2010, 59(1): 25-28.
[5] Seow Y, Rahimifard S. A framework for modelling energy consumption within manufacturing systems[J]. CIRP Journal of Manufacturing Science and Technology, 2011, 4(3): 258-264.
[6] Mouzon G, Yildirim M B, Twomey J. Operational methods for minimization of energy consumption of manufacturing equipment[J]. International Journal of Production Research, 2007, 45(18/19): 4247-4271.
[7] Mouzon G, Yildirim M B. A framework to minimise total energy consumption and total tardiness on a single machine[J]. International Journal of Sustainable Engineering, 2008, 1(2): 105-116.
[8]  B, Pater J P, Honiden S, et al. A multiobjective evolutionary approach to scheduling for evolving manufacturing systems[J]. Evolving Systems, 2012, 3(1): 31-44.
B, Pater J P, Honiden S, et al. A multiobjective evolutionary approach to scheduling for evolving manufacturing systems[J]. Evolving Systems, 2012, 3(1): 31-44.
[9] Drake R, Yildirim M B, Twomey J, et al. Data collection framework on energy consumption in manufacturing[C]// 2006 IIE Annual Conference and Exposition. Orlando: Institute of Industrial Engineers, 2006: 1-6.
[10] Fang Kan, Nelson U, ZHAO Fu, et al. A new approach to scheduling in manufacturing for power consumption and carbon footprint reduction[J]. Journal of Manufacturing Systems, 2011, 30(4): 234-240.
[11] 刘向. 面向节能的流程工业生产调度建模与求解方法研究[D]. 长沙: 国防科学技术大学机电工程与自动化学院, 2008: 13-16.
LIU Xiang. Modeling and solving of production scheduling for process industry based on saving energy[D]. Changsha: National University of Defense Technology. School of MechanicalEngineering and Automation, 2008: 13-14.
[12] 李凯. 考虑节能降耗的关键机器调度问题研究[D]. 合肥: 合肥工业大学管理学院, 2009: 42-44.
LI Kai. Key-machine scheduling problems with consideration of energy conservation[D]. Hefei: University of Science and Technology of China. School of Management, 2009: 42-44.
[13] 印二威. 面向节能的铝上业生产调度问题模型与算法研究[D]. 长沙: 国防科学技术大学机电工程与自动化学院, 2010: 23-27.
YIN Erwei. Study on model and algorithm of scheduling in aluminum industry process for energy saving[D]. Changsha: National University of Defense Technology. School of MechanicalEngineering and Automation, 2010: 23-27.
[14] Hejazi S R, Saghafian S. Flowshop-scheduling problems with makespan criterion: A review[J]. International Journal of Production Research, 2005, 43(12): 2895-2929.
[15] Ribas I, Companys R, Martorell X T. Comparing threestep heuristics for the permutation flow shop problem[J]. Computers & Operations Research, 2010, 37(12): 2062-2070.
[16] HE Yaohua, HUI Chiwai. A rule-based genetic algorithm for the scheduling of single-stage multi-product batch plants with parallel units[J]. Computers and Chemical Engineering, 2008, 32(12): 3067-3083.
[17] Taillard E. Scheduling instances[EB/OL]. [2012-07-17]. http://mistic.heig-vd.ch/taillard/problemes.dir/ordonnancement.dir/ordonnancement.html
(编辑 赵俊)
收稿日期:2012-11-01;修回日期:2013-01-25
基金项目:国家科技支撑计划项目(2012BAF12B10);教育部人文社科青年项目(12YJCZH129);广东省教育部产学研结合项目(2011A090200050);广东省重大科技专项(2012A080104022);广东省科技计划项目(2011B01070052,2012B010500027,2012B010900064)
通信作者:刘国胜(1983-),男,湖北武汉人,博士研究生,讲师;从事低碳制造、调度优化等研究;电话:15017554121;E-mail: gliu@gdut.edu.cn