基于Petri网的OHT搬运系统防死锁调度方法
刘晓斌,周炳海
(同济大学 机械与能源工程学院,上海,201804)
摘要:为了有效预防高空提升运输(OHT)小车运行过程中可能出现的碰撞及死锁现象,提高OHT搬运系统的运行效率,提出一种防死锁调度方法。首先,利用Petri网建立OHT小车搬运系统模型,在分析Petri网模型的基础上,证明有效避免死锁的控制规则。接着结合匈牙利算法构建防死锁调度方法,通过轨道节点的时间窗预测OHT小车下一步路径状况,避免小车碰撞和死锁现象,实现多台OHT小车的优化调度。最后,进行仿真实验及对比分析。研究结果表明:本文提出的防死锁调度方法是有效可行的。
关键词:OHT;调度;死锁;Petri网
中图分类号:TP29 文献标志码:A 文章编号:1672-7207(2013)11-4745-08
Deadlock-free scheduling of OHT transport systems based on Petri nets
LIU Xiaobin, ZHOU Binghai
(School of Mechanical Engineering, Tongji University, Shanghai 201804, China)
Abstract: To simultaneously solve the problems of collision and deadlock in overhead hoist transport (OHT) systems, and improve the transport efficiency of OHT vehicles, a deadlock-free scheduling method of OHT vehicles was proposed. Firstly, an OHT transport system model was built with Petri nets, and a deadlock-free control rule was presented after analyzing the Petri net model. Then a deadlock-free scheduling method combining Hungarian algorithm was put forward based on the deadlock-free control rule. Using time-windows theory to forecast one step ahead, the optimal scheduling of multi OHT vehicles was realized with vehicle collision and system deadlock. At last, simulation experiments were carried out and the proposed method was compared with other scheduling method. The results indicate that it is feasible and valid for implementing the deadlock-free scheduling method on OHT transport systems.
Key words: OHT; scheduling; deadlock; Petri net
高空提升运输(overhead hoist transport, OHT)因其不需占用地面空间,且能提高搬运效率,已被广泛应用于直径为300 mm晶圆制造工厂的自动物料搬运系统(Automated material handling systems, AMHSs)中。在直径为300 mm晶圆制造工厂整体式布局中,搬运设备无需经过暂存区(Stocker)转运而直接进行设备到设备的搬运,这种方式虽然提高了搬运效率,但容易引起OHT小车碰撞、堵塞甚至进一步扩散导致死锁。如何有效消除碰撞、规避死锁现象,使搬运系统流畅运行,是目前OHT搬运系统调度中亟须解决的关键问题。近年来,诸多国内外学者对于物料搬运系统的路径调度问题进行了研究。Kim等[1]利用Dijkstra算法进行了单个AGV的路径调度规划。Ho等[2]提出了一种划分区域以避免AGV小车冲突的调度方法。Correa等[3]采用混合整数规划解决AGV小车的调度问题并实现路径优化。Tanaka等[4-5]利用Petri网分解方法进行了AGV的路径优化。Petri网作为一种有效的图形化建模工具,被广泛应用于分析搬运系统的冲突及死锁现象。Dotoli等[6]提出了一种有色时延Petri网(TPN)建模方法,对AGV系统进行了建模与监控。Wu等[7]采用面向资源的着色Petri网(CROPN)对AGV系统路径进行布局和建模,并提出了一种能避免死锁与冲突的运行规则。Wu等[8]在文献[7]的基础上研究了双向AGV系统的防死锁路径优化。以上研究是针对AGV系统的,在防死锁策略中,常在系统中保持一定量的缓冲区(buffer)资源空闲以避免形成循环等待。但在OHT搬运系统中工站间没有设置buffer,若采取上述防死锁策略,必须使某些设备空闲,导致系统整体产出受到严重影响。目前,针对OHT搬运系统的研究大多侧重小车的调度问题[9-11],对于OHT小车运行过程可能出现的碰撞、路径冲突及死锁问题的研究鲜有报道。Yang等[12]对进行工站之间直接搬运的OHT小车系统进行了研究,提出将第K短路径法和路径中运行的OHT小车数相结合的方法进行路径的无冲突调度,但是,该文献采用模糊估计的方法,规避冲突的有效性有待提高。Kuo等[13-14]从不同的角度利用Petri网对OHT搬运系统进行了建模和性能评价研究,但都没有涉及核心的死锁预防问题。Im等[15]利用有向图表示OHT小车之间的等待关系,从中识别出死锁现象并通过改变部分OHT小车路径解除死锁,但该方法不能预测系统可能产生死锁的位置并提前预防,不适用于实际生产调度。针对目前在OHT搬运系统调度中未能有效考虑堵塞、碰撞及死锁的情况,本文作者考虑AMHS中OHT小车搬运的特点,提出一种规避碰撞和预防死锁的调度方法。
1 问题描述
目前,在直径300 mm晶圆制造工厂中最常见的AMHSs系统采用的是脊柱型布局[16],根据生产工艺的不同,将相似工艺的加工设备放置在同一制程区间(Bay)内,Intrabay系统负责Bay内的物料搬运;Interbay系统负责在Bay间的物料搬运。OHT小车以晶舟为单位进行运输,晶舟容量为25片晶圆,1台OHT小车1次只能运输1个晶舟。OHT小车在轨道上单向行进,小车轨道位于加工设备的上货端口之上,在搬运过程中,通过升降装置将晶舟从设备的上货端口(Port)送达OHT小车或者由OHT小车装载到设备的上货端口。典型AMHSs系统的布局如图1所示。
OHT小车的调度问题可以视为一个指派问题。假设系统中有n台可用的OHT小车将要被分配去搬运l个待搬运的晶舟,通过解决该问题使得相关目标最优化。本文所要解决的OHT小车指派问题可以表示为:
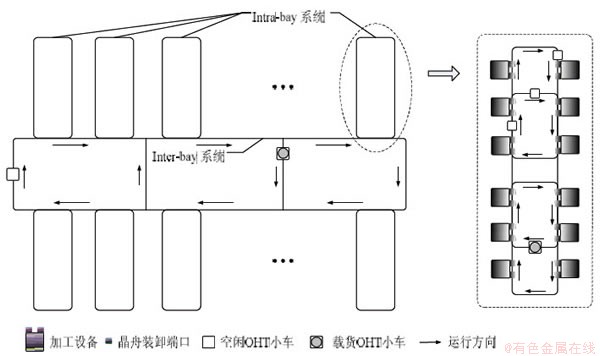
图1 自动物料搬运系统(俯视)
Fig.1 Automated material handling system
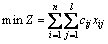
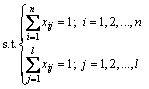

为了更好地表示OHT小车搬运系统运行过程,运用Petri网对其进行建模。
定义1个Petri网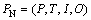 ,
,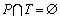 ,
, 。
。 是库所的有限集合;
是库所的有限集合;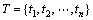 是变迁的有限集合;
是变迁的有限集合; 是输入函数,它定义了从P到T的有向弧的重复数或者权重的集合;
是输入函数,它定义了从P到T的有向弧的重复数或者权重的集合;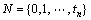 为非负整数集;同理,
为非负整数集;同理,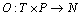 是输出函数,它定义了从T到P的有向弧的重复数或者权重的集合。
是输出函数,它定义了从T到P的有向弧的重复数或者权重的集合。
图2所示为Intrabay搬运系统的逻辑示意图。该系统中包含12个节点和3台OHT小车,N代表轨道节点,V表示OHT小车,OHT小车的路径和运行方向如图2所示,每个节点最多只能停留1台OHT小车,并且某些回路具有OHT小车容量限制。
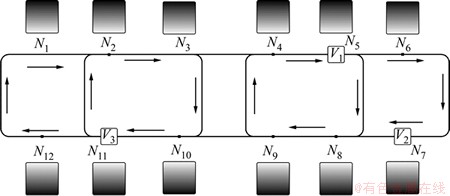
图2 OHT小车运行示意图(俯视)
Fig.2 Circulation of OHT vehicles
为了尽可能减少堵塞,OHT小车在没有搬运任务时依然在轨道上运行,小车只有在节点即晶舟装卸端口可以停下,可以将节点视为一种资源,定义为资源库所。库所中的令牌代表该节点中停留的小车。变迁表示小车由一个节点向另一个节点的转移,根据变迁连接这些节点,就可以得到OHT小车搬运系统的Petri网模型。OHT小车搬运系统的Petri网模型如图3所示。每个库所代表OHT搬运系统中的1个节点,任何2个库所间均只有1个变迁。
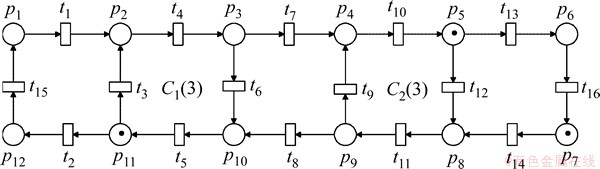
图3 OHT小车搬运过程Petri网模型
Fig.3 Petri net model for transporting progress of OHTs vehicles
定义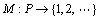 为Petri网的标识,其第i个元素表示第i个库所中的令牌数,Petri网的标识M表示OHT小车搬运系统的状态。
为Petri网的标识,其第i个元素表示第i个库所中的令牌数,Petri网的标识M表示OHT小车搬运系统的状态。
记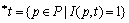 为变迁t的所有输入库所的集合,称为t的前集,
为变迁t的所有输入库所的集合,称为t的前集,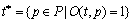 为变迁t的所有输出库所的集合,称为t的后集。类似地,*p和p*分别表示库所p的前集和后集。
为变迁t的所有输出库所的集合,称为t的后集。类似地,*p和p*分别表示库所p的前集和后集。
定义1 在标识为M的有限容量的Petri网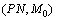 中,其某一变迁
中,其某一变迁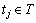 发生的条件是对任意
发生的条件是对任意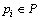 ,
,

且
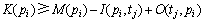
其中:K为PN上的容量函数。
该定义表明如果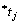 中含有足够的令牌,且
中含有足够的令牌,且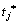 中所有的库所具有足够多的空间,变迁tj就会被激发。其中第1个条件满足,称为tj流程使能,第2个条件满足,称为tj资源使能。tj的发生使得Petri网的标识M变成如下定义的新标识
中所有的库所具有足够多的空间,变迁tj就会被激发。其中第1个条件满足,称为tj流程使能,第2个条件满足,称为tj资源使能。tj的发生使得Petri网的标识M变成如下定义的新标识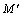 即
即
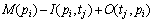 。
。
2 防死锁控制规则
OHT搬运系统的死锁现象会严重影响系统的性能,使系统陷入停顿,所以在搬运系统调度规则的设计中必须避免系统死锁。
形成系统死锁必须满足4个条件:(1) 相互抑制(mutual exclusion):一个资源每次只能被一个进程使用;(2) 持有并等待(hold and wait):持有资源的进程允许申请其他资源;(3) 非剥夺条件(no preemption):除非资源被释放,否则一个资源不允许被强行剥夺;(4) 循环等待 (circular wait)存在一个进程等待队列 ,其中p1等待p2占有的资源,p2等待p3占有的资源,…,pn等待p1占有的资源,形成一个进程等待回路。在整体式OHT搬运系统中,资源就是路径中的节点,过程就是小车的前进,易知前3个条件必然成立,因此,唯一能避免搬运系统死锁的方法是保证第4个条件不会被满足。
,其中p1等待p2占有的资源,p2等待p3占有的资源,…,pn等待p1占有的资源,形成一个进程等待回路。在整体式OHT搬运系统中,资源就是路径中的节点,过程就是小车的前进,易知前3个条件必然成立,因此,唯一能避免搬运系统死锁的方法是保证第4个条件不会被满足。
在OHT搬运系统中,任一区域的OHT小车都能通过一定的路径到达其他任一区域,否则,OHT小车搬运系统就是无效的系统。因此,表示该OHT小车搬运系统的Petri网模型必然是强连接并且由若干个回路组成。对于强连接的无限容量Petri网模型,若初始标识M0中存在令牌,则其具有活性。此时模型若产生死锁,则是由于库所的有限容量造成的,使OHT小车搬运系统无死锁就是建立一个控制规则使有限容量的Petri网模型具有活性。
用Ci表示模型中的一个回路,如C1={p2, t4, p3, t 6, p10, t5, p11, t3, p2}是图3中的一条回路。用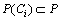 表示回路Ci上的库所集,用
表示回路Ci上的库所集,用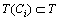 表示回路Ci上的变迁集。相应地,用
表示回路Ci上的变迁集。相应地,用 ,
,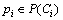 表示回路Ci的容量;用
表示回路Ci的容量;用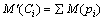 ,
,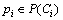 表示回路Ci中令牌的数目;用
表示回路Ci中令牌的数目;用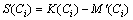 表示回路Ci中可用空间数。
表示回路Ci中可用空间数。
在OHT小车搬运系统的Petri网模型中,回路可能是交互的,所以,不同的回路上可能会具有相同的库所。令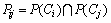 为回路Ci和Cj的共享库所集,
为回路Ci和Cj的共享库所集,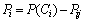 ,
,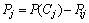 。
。
下面给出OHT小车搬运系统中回路上避免死锁的条件。
定理1 在标识M下,若每一个回路Ci均至少含有一个非共享可用空间,则OHT小车搬运系统的Petri网模型具有活性。
证明:用Cn表示OHT搬运系统的Petri网模型中由n个回路构成的子网模型。若能证明n为任一正整数时,Cn均符合定理1,则可确定防死锁规则。
当n=1时,在标识M下,有以下几种情形。
情形1:若S(C)=1,则存在1个库所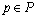 (或
(或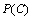 )使得
)使得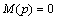 ,且库所p唯一的输入变迁
,且库所p唯一的输入变迁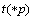 必须是流程使能。则此变迁t可以激发。变迁t发生之后,库所*t,比如p1拥有了可用空间,则变迁t(*p1)就可以发生。通过这样的方式,无论标识M如何改变,回路C上的每一个变迁都能够重新激发,即系统具有活性。
必须是流程使能。则此变迁t可以激发。变迁t发生之后,库所*t,比如p1拥有了可用空间,则变迁t(*p1)就可以发生。通过这样的方式,无论标识M如何改变,回路C上的每一个变迁都能够重新激发,即系统具有活性。
情形2:若S(C)>1,系统中总是有OHT小车对于 和任意流程使能的变迁
和任意流程使能的变迁 ,存在1个库所集
,存在1个库所集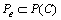 或
或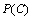 使得
使得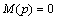 。则
。则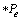 中的变迁可以激发。
中的变迁可以激发。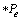 发生后,存在1个库所集与
发生后,存在1个库所集与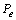 相似,因此,另外一组变迁集可以激发。通过这样的方式,系统仍具有活性。
相似,因此,另外一组变迁集可以激发。通过这样的方式,系统仍具有活性。
当n>1时,假设一个由k个回路构成的子网模型 具有活性,通过添加1个新的回路
具有活性,通过添加1个新的回路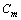 ,构成一个由k+1个回路构成的子网模型
,构成一个由k+1个回路构成的子网模型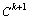 ,如图4所示。若该模型中的每一个回路都有一个非共享的可用空间,则只需证明回路
,如图4所示。若该模型中的每一个回路都有一个非共享的可用空间,则只需证明回路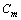 上的变迁t1, t2, …, tk及tk+1具有活性即可。
上的变迁t1, t2, …, tk及tk+1具有活性即可。
情形1:若分配给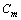 的可用空间在与
的可用空间在与 共用的库所中,则由于
共用的库所中,则由于 的活性,库所
的活性,库所 将在某一时刻清空。此时变迁tk+1可以激发,同理tk, …, t2均能激发,这些变迁发生后,
将在某一时刻清空。此时变迁tk+1可以激发,同理tk, …, t2均能激发,这些变迁发生后, 上的每一个回路仍都有一个非共享可用空间,故
上的每一个回路仍都有一个非共享可用空间,故 仍具有活性。
仍具有活性。
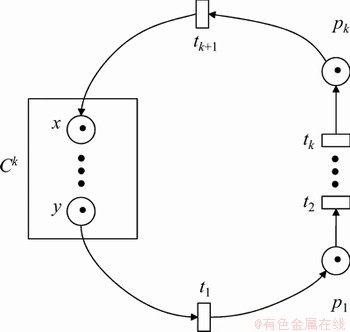
图4 k+1回路子网模型Ck+1
Fig.4 Petri net model of Ck+1 formed by k+1 circuits
情形2:若分配给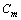 的可用空间存在于p1, p2, …, pk中的任一库所,则该空间可以移入库所p1。同理,
的可用空间存在于p1, p2, …, pk中的任一库所,则该空间可以移入库所p1。同理, 具有活性,一个令牌可移入y,则t1可以激发,
具有活性,一个令牌可移入y,则t1可以激发,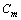 中的空间移入与
中的空间移入与 共用的库所中,则
共用的库所中,则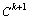 具有活性。
具有活性。
为了使系统具有活性,必须保证在控制交互输入变迁的激发次序时,定理1的条件得到满足。
若一个变迁t不在回路Ci上,但其输出库所t*在回路Ci上,则称变迁t是回路Ci的输入变迁。在OHT搬运系统的Petri网模型中,一个回路Ci可能有2个或2个以上的输入变迁,用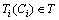 表示回路Ci的变迁集合。若触发变迁
表示回路Ci的变迁集合。若触发变迁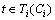 后,系统中所有的回路仍满足定理1的条件,则此Petri网模型是无死锁的。因此只需观测系统的实时状态,计算每个回路Ci的可用空间S(Ci),控制Ti(Ci)中的变迁,使得定理1中的条件得以满足。根据以上分析可得如下定理。
后,系统中所有的回路仍满足定理1的条件,则此Petri网模型是无死锁的。因此只需观测系统的实时状态,计算每个回路Ci的可用空间S(Ci),控制Ti(Ci)中的变迁,使得定理1中的条件得以满足。根据以上分析可得如下定理。
定理2 若回路Ci上的容量K(Ci)小于等于系统中小车数,则回路Ci上可能发生死锁。
证明:采用反证法。若回路Ci上的容量K(Ci)大于系统中的小车数,则该回路上至少含有一个非共享的可用空间,根据定理1,此时,回路Ci具有活性。因此,若回路Ci发生死锁,K(Ci)必然小于等于系统中的OHT小车数。
根据定理2,只需在计算S(Ci)后识别部分回路并对其进行控制。如图3所示的例子,这些回路分别是C1,C2和C3,而只有变迁t3,t6,t7,t5及t11需要加以控制。
3 无死锁调度方法设计
晶圆制造工厂是一个非常复杂的系统,自动物料搬运系统调度优化必须在尽可能提高搬运系统效率的同时又不影响生产系统整体产出的提升。
首先考虑影响搬运效率的因素。假设模型中OHT小车数为NV,Bay的数目为NBay,每个Bay中有NM个工站。搬运完成时间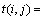
 ,其中,晶舟装载时间tl和晶舟卸载时间tu默认为常数;搬运时间
,其中,晶舟装载时间tl和晶舟卸载时间tu默认为常数;搬运时间 ;D(i, j)为小车Vi与搬运任务Jj目的地间的最短距离;v为OHT小车平均运行速度。一般假设OHT小车匀速运行,因此,最短距离成为影响搬运系统效率的实际因素。定义搬运任务的到达率为
;D(i, j)为小车Vi与搬运任务Jj目的地间的最短距离;v为OHT小车平均运行速度。一般假设OHT小车匀速运行,因此,最短距离成为影响搬运系统效率的实际因素。定义搬运任务的到达率为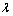 ,模型运行时间长度为T,共有NJ个搬运任务,则系统的搬运负荷为
,模型运行时间长度为T,共有NJ个搬运任务,则系统的搬运负荷为
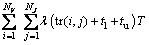 。搬运系统的总能力
。搬运系统的总能力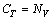 ×
×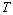 ,故搬运负荷系数
,故搬运负荷系数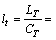
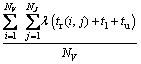 。
。
此外,在搬运系统调度规则的设计中应该考虑到工站的加工负荷,以获得较好的生产系统整体产出。本文主要考虑晶舟的等待时间Twj,一方面,等待时间在生产中属于非增值时间,晶舟在某一工站等待过久容易造成瓶颈工序影响整体产出;另一方面,在一些特定的工序中,滞留超过一定时间可能会造成晶舟损坏。定义加工任务Jj的操作时间为P j,则系统整体加工负荷为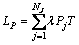 。系统整体产能
。系统整体产能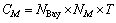 ,则系统加工负荷系数
,则系统加工负荷系数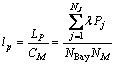 。计算工站Mk加工负荷
。计算工站Mk加工负荷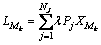 ,其中
,其中 ,因此,工站Mk的加工负荷系数
,因此,工站Mk的加工负荷系数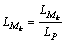 。
。
综上可见:在OHT搬运系统调度中同时考虑最短搬运距离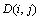 及晶舟等待时间TWj这2个因素,其权重则根据系统的搬运负荷和加工负荷进行调节以获得系统资源的平衡。令搬运距离权重
及晶舟等待时间TWj这2个因素,其权重则根据系统的搬运负荷和加工负荷进行调节以获得系统资源的平衡。令搬运距离权重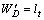 ,等待时间权重
,等待时间权重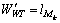 ,归一化得
,归一化得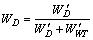 ,
, 。则OHT小车指派问题中成本函数
。则OHT小车指派问题中成本函数 (其中,Dmax为搬运任务Jj与所有空闲OHT小车当前距离中最大的距离;Twmax为当前系统中等待最久的晶舟等待时间)。
(其中,Dmax为搬运任务Jj与所有空闲OHT小车当前距离中最大的距离;Twmax为当前系统中等待最久的晶舟等待时间)。
计算出成本函数后,采用匈牙利算法进行OHT小车调度,同时嵌入防死锁控制规则构建防死锁调度方法。同时,为了避免多台OHT小车在同一时间经过同一节点而产生碰撞,引入时间窗进行路径规划,采用预测下一步路径的方法判断可能产生的碰撞并在路径规划中加以避免。该调度方法流程如下。
步骤1 更新系统状态,若系统生成新的搬运任务或OHT小车卸载完毕,转至步骤2,否则停止。
步骤2 计算当前空闲小车与待分配搬运任务的多因素成本函数矩阵: 。其中,n和l分别表示当前空闲小车与待分配搬运任务数。
。其中,n和l分别表示当前空闲小车与待分配搬运任务数。
步骤3 标准化成本函数矩阵,若空闲小车数与搬运任务数不相等,则需要添加相应数量的虚拟小车或任务,获得一个k×k阶的新矩阵C1。
步骤4 矩阵C1中所有元素减去所在行中最小的元素,获得新的缩减矩阵C2;矩阵中C2所有元素减去所在列中最小的元素,获得新矩阵C3。
步骤5 计算能覆盖矩阵C3当前所有0元素的最少直线数x,若x=k,则已找到最优指派方案,转入步骤7,否则转入步骤6。
步骤6 找出矩阵C3中未被任何直线覆盖的各元素,均减去其中最小元素y,矩阵中被2条直线覆盖的各元素均加上y,获得矩阵C4,转至步骤5。
步骤7 OHT小车接受指令,初始化标识M0,确定目标标识Mg,记录接受指令的时间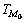 ,即初始状态为
,即初始状态为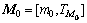 。
。
步骤8 根据已分配任务OHT小车的起点和终点和每个任务完成时间,从大到小对k台OHT小车搬运任务进行排序。
步骤9 对用时最长的任务进行路径规划, 提前一步计算回路的可用空间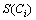 ,对于满足定理1的使能变迁ti,安排其激发时间,并根据OHT小车进入和离开各个节点的时间,得出预留时间窗
,对于满足定理1的使能变迁ti,安排其激发时间,并根据OHT小车进入和离开各个节点的时间,得出预留时间窗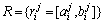 及空闲时间窗
及空闲时间窗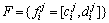 。
。
步骤10 对用时第二长的OHT小车路径进行规划。对于使能的变迁ti,若在其输出库所时间窗中存在第k个空闲时间段满足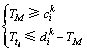 ,其中,
,其中,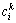 和
和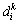 分别是变迁ti目标节点第k段预留时间窗的开始和结束时间,为变迁ti的触发时间,则ti可在
分别是变迁ti目标节点第k段预留时间窗的开始和结束时间,为变迁ti的触发时间,则ti可在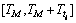 时间段触发,更新时间窗,在R中增加
时间段触发,更新时间窗,在R中增加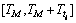 ,在F中删减相应时段。得出第2台OHT小车的路径规划。
,在F中删减相应时段。得出第2台OHT小车的路径规划。
步骤11 在前k-1台OHT小车的空闲时间窗上对用时第k个任务进行无死锁路径规划,重复执行,直到规划完所有可行的路径。
步骤12 转至步骤1。
4 仿真实验分析
采用VB编程语言实现本文所提调度方法,嵌入ARENA仿真模型中运行。在主频1.6 GHz、内存3 GB、Intel(R) Core(TM)2 Duo CPU的便携式计算机上进行仿真实验。
为有效评价本文提出的调度算法,用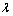 表示搬运任务的到达率,即系统在
表示搬运任务的到达率,即系统在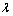 时间内要进行一次任务搬运,该时间服从正态分布
时间内要进行一次任务搬运,该时间服从正态分布 ;TAW表示平均任务等待时间,表征制造系统的空闲率,该值越小,说明调度策略越好;TAV表示平均搬运时间,表征物料搬运系统的运行效率,该值越小,说明调度策略越好;TAL表示平均任务完成时间,表征物料搬运系统的响应速度和搬运效率,该值越小,说明调度策略越好;UO表示OHT小车的利用率,表征系统中搬运系统的搬运效率,该值越大,说明调度策略越好。
;TAW表示平均任务等待时间,表征制造系统的空闲率,该值越小,说明调度策略越好;TAV表示平均搬运时间,表征物料搬运系统的运行效率,该值越小,说明调度策略越好;TAL表示平均任务完成时间,表征物料搬运系统的响应速度和搬运效率,该值越小,说明调度策略越好;UO表示OHT小车的利用率,表征系统中搬运系统的搬运效率,该值越大,说明调度策略越好。
4.1 搬运任务到达率对搬运效率的影响
令NBay=4;NM=6;NV=10,改变λ的均值μ,求出TAW,TAV和TAL,分析搬运任务时间分布变化对搬运效率的影响。仿真结果如图5所示。
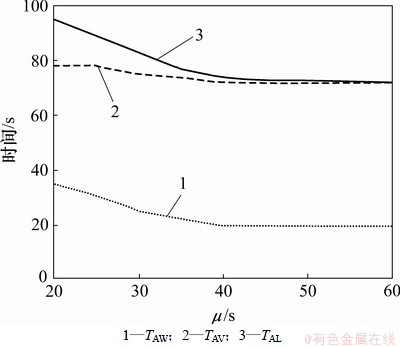
图5 λ对搬运效率的影响
Fig.5 Relationship with λ and transport efficiency
由图5可知:随着μ的增大,系统的平均等待时间逐渐减小,在μ大于40之后渐趋平稳;而在μ逐渐增大的过程中,TAV和TAL也逐渐减小且趋于平稳,同时TAL逐渐趋近于TAV,这表明搬运系统响应速度提升,任务空闲等待的时间趋于0 s。这说明对于不同繁忙程度的搬运任务,该调度方法具有良好的适应性。
4.2 Bay数量对搬运效率的影响
令NM=6;NV=10,分别令NBay=4及NBay=8;求出T AW,TAV和TAL相对于μ的变化趋势,比较不同Bay数下的搬运效率。仿真结果如图6所示。
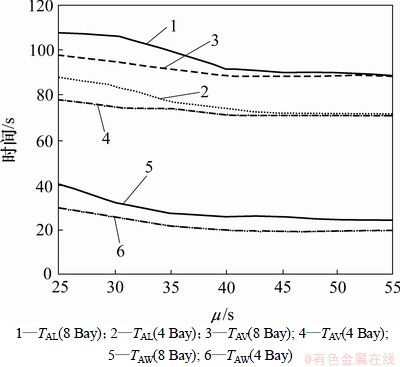
图6 Bay的数目对搬运效率的影响
Fig.6 Relationship with NBay and transport efficiency
由图6可知:随着物料搬运系统内Bay数量的增加,搬运路径变得更长更复杂,因此,TAW,TAV和TAL都随之增大,不过其值波动不大,尚在能够接受的范围之内,表明该调度方法适用于复杂系统的物料搬运调度。
4.3 小车数和搬运任务到达率对小车利用率的影响
令NBay=4,NM=6;分别令NV=5,7,10,15,20,比较不同的搬运任务到达率下OHT小车的利用率,分析OHT小车数和任务到达时间分布对搬运效率的综合影响。仿真结果如图7所示。
由图7可知:当小车数一定时,UO随着μ的增大而减小;在任务生成时间服从某一确定分布时,UO随着OHT小车数的增加而减少,最后趋于平稳。这表明OHT小车数影响到半导体制造系统的生产效率和物料搬运系统的运行效率,需要根据不同的情况选择不同的OHT小车数。
4.4 与其他调度方法的比较
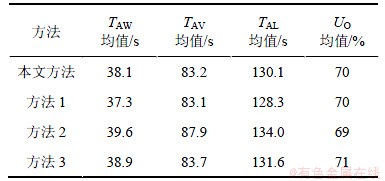
选用3种调度方法与本文方法进行比较分析。方法1不考虑系统中OHT小车之间可能出现的碰撞、堵塞、死锁等因素,结合最短路径法与最早完工时间进行调度;方法2选用文献[12]的方法,充分考虑冲突等因素,但每一条路径上只允许1辆OHT小车占用,结合时间窗理论进行调度;方法3选用文献[9]的方法,考虑可能的碰撞问题及第K短路径中现有OHT小车的数量,选择OHT小车数量最小的路径进行调度,尽量避免冲突。令NBay=4;NM=6;NV=10,λ~N(25,5)。各方法分别运行10次,实验结果均值如表1所示。
由表1可知:本算法在平均任务等待时间、平均OHT小车搬运时间和平均任务完成时间这3个性能指标上都较方法2与方法3的优。虽然方法1的性能指标略优于本文方法,但前者没有考虑路径冲突和死锁问题,而本文的方法能有效地规避路径冲突、车辆碰撞,在调度过程中嵌入了防死锁规则,且两者性能参数相差不大,所以,比较结果都是在可接受范围之内。由此,用本文提出的调度方法进行OHT小车调度能够获得较高的搬运效率,提高半导体制造系统的生产效率。

图7 λ和NV对OHT小车利用率的影响
Fig.7 Relationship with λ/NV and transport efficiency
表1 4种不同调度方法对比
Table 1 Comparisons of four different scheduling methods
5 结论
(1) 在证明OHT搬运系统防死锁规则的基础上,构建了基于Petri网的OHT搬运系统防死锁调度方法,结合轨道节点的时间窗预测路径状况,实现多台OHT小车的优化调度。
(2) 对于不同繁忙程度的搬运任务,本文所提出的调度方法具有良好的适应性。在搬运系统规模增大时,表征搬运效率的指标值波动尚在能够接受的范围之内,该调度方法适用于复杂系统的物料搬运调度。
(3) 在与文献所提的其他3种调度方法进行比较中,本文提出的调度方法能够在避免碰撞和死锁的基础上获得较高的搬运效率。
参考文献:
[1] Kim C W, Tanchoco I M A. Conflict-free shortest-time bi-directional AGV routing[J]. International Journal of Production Research, 1991, 29(12): 2377-2391.
[2] Ho Y C, Liao T W. Zone design and control for vehicle collision prevention and load balancing in a zone control AGV system[J]. Computers & Industrial Engineering, 2009, 56: 417-432.
[3] Correa A I, Langevin A, Rousseau L M. Scheduling and routing of automated guided vehicles: A hybrid approach[J]. Computers and Operations Research, 2007, 34(6): 1688-1707.
[4] Tanaka Y, Nishi T, Inuiguchi M. Dynamic optimization of simultaneous dispatching and conflict-free routing for automated guided vehicles-Petri net decomposition approach[J]. Journal of Advanced Mechanical Design, Systems, and Manufacturing, 2010, 4(3): 701-715.
[5] Nishi T, Maeno R. Petri Net decomposition approach to optimization of route planning problems for AGV systems[J]. IEEE Transactions on Automation Science and Engineering, 2010, 7(3): 523-537.
[6] Dotoli M, Fanti M P. Coloured timed Petri net model for real-time control of automated guided vehicle systems[J]. International Journal of Production Research, 2004, 42(9):1787-1814.
[7] WU Naiqi, ZENG Wenqu. Deadlock avoidance in an automated guidance vehicle system using a coloured Petri net model[J]. International Journal of Production Research, 2002, 40(1): 223-238.
[8] WU Naiqi, ZHOU Mengchu. Shortest routing of bidirectional automated guided vehicles avoiding deadlock and blocking[J]. IEEE/ASME Transactions on Mechatronics, 2007, 12(1): 63-72.
[9] Liao D Y, Fu H S. A simulation-based, two-phase approach for dynamic OHT allocation and dispatching in large-scaled 300 mm AMHS management[J]. IEEE Robotics & Automation Magazine, 2004, 11(3): 22-32.
[10] Kim B I, Shin J, Jeong S. Effective overhead hoist transport dispatching based on the Hungarian algorithm for a large semiconductor FAB[J]. International Journal of Production Research, 2009, 47(10): 2823-2834.
[11] Wu L H, Mok P Y, Zhang J. An adaptive multi-parameter based dispatching strategy for single-loop inter-bay material handling systems[J]. Computers in Industry, 2011, 62(2): 175-186.
[12] Yang J W, Cheng H C, Chiang T C, et al. Multi-objective lot scheduling and dynamic OHT routing in a 300-mm wafer fab[C]// Proceedings of the IEEE International Conference on Systems, Man and Cybernetics. Singapore: IEEE, 2008: 1608-1613.
[13] Kuo C H. Modelling and performance evaluation of an overhead hoist transport system in a 300 mm fabrication plant[J]. International Journal of Advanced Manufacturing Technology, 2002, 20(2): 153-161.
[14] Liao D Y, Jeng M D, Zhou M C. Application of Petri nets and lagrangian relaxation to scheduling automatic material-handling vehicles in 300-mm semiconductor manufacturing[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part C: Applications and Reviews, 2007, 37(4): 504-516.
[15] Im K, Kim K, Moon Y, et al. The deadlock detection and resolution method for a unified transport system[J]. International Journal of Production Research, 2010, 48(15): 4423-4435.
[16] Wright R, Cunningham C, Benhayoune K, et al. 300 mm factory layout and automated materials handling[J]. Solid State Technol, 1999, 42(12): 35-42.
(编辑 赵俊)
收稿日期:2012-12-10;修回日期:2013-02-28
基金项目:国家自然科学基金资助项目(61273035,71071115);国家高技术研究发展计划(“863”计划)项目(2009AA043000)
通信作者:周炳海(1965-),男,浙江浦江人,博士,教授,博士生导师,从事制造系统/物流系统调度、建模、仿真与预防性维护研究;电话:021-69589598;E-mail: bhzhou@tongji.edu.cn