连续排水边界下成层地基一维固结问题的有限元分析
蔡烽1, 2,何利军3,周小鹏1,梅国雄1, 3
(1. 南京工业大学 交通学院,江苏 南京,210009;
2. 温州市建筑设计研究院,浙江 温州,325003;
3. 南昌航空大学 土木建筑学院,江西 南昌,330063)
摘要:基于ABAQUS有限元软件开发连续排水边界条件的子程序,将计算结果分别与单层地基经典的Terzaghi一维固结理论解和连续排水边界Terzaghi一维固结解析解以及双层地基一维固结解析解进行对比分析,验证计算结果的正确性。针对实际工程中常见的成层地基,采用变化弹性模量、渗透系数和泊松比的方法对连续排水边界下成层地基一维固结问题进行数值分析。研究结果表明:连续排水边界能良好地模拟接近实际的工程工况。
关键词:太沙基一维固结方程;连续排水边界;有限元分析;成层地基
中图分类号:TU 471.4 文献标志码:A 文章编号:1672-7207(2013)01-0315-09
Finite element analysis of one-dimensional consolidation problem with continuous drainage boundaries in layered ground
CAI Feng1, 2, HE Lijun3, ZHOU Xiaopeng1, MEI Guoxiong1, 3
(1. College of Transportation Engineering, Nanjing University of Technology, Nanjing 210009, China;
2. Wenzhou Architectural Design & Research Institute, Wenzhou 325003, China;
3. College of Civil Engineering and Architecture, Nanchang Hangkong University, Nanchang 330063, China)
Abstract: Based on the finite element analysis of software ABAQUS, the one-dimensional subroutine of continuous drainage boundaries was developed. Results comparison among the classic Terzaghi’s one-dimensional consolidation theory, the analytical solutions of Terzaghi’s one-dimensional consolidation equation with continuous drainage boundaries and the analytical solutions of one-dimensional consolidation for a double-layered ground to verify the correctness. According to the layered ground of practical engineering, one-dimensional consolidation problem with continuous drainage boundaries in layered ground was investigated by using changes in different elastic moduli, permeability coefficients and poisson’s ratios with the finite element analysis. The results show that continuous drainage boundaries can simulate the practical engineering commendably.
Key words: Terzaghi’s one-dimensional consolidation equation; continuous drainage boundaries; finite element analysis;layered ground
固结是土力学中的重要课题,得到广泛而深入地研究,其主要由固结方程、边界条件和初始条件3部分组成。目前Terzaghi[1]的一维固结理论应用的最广泛,许多研究者[2-5]在其6个基本假定基础上进行修正及推广。Gibson等[6]修改Terzaghi固结理论的小变形假设前提,提出一维大变形固结理论。谢康和等[7-8]在Terzaghi固结的基础上,给出外荷载随时间变化时更为普遍的大变形固结理论。当前,固结理论研究的工作主要集中在变化不同的本构关系以及初始条件即荷载条件的问题上求解,而有关边界条件的研究相对较少。Terzaghi一维固结理论是针对透水与不透水这2种极端的边界条件,但在实际工程中,土层的边界条件可能存在介于透水与不透水之间的不同透水程度的边界条件,而且土层上、下2面边界的透水程度可能往往不同。理论上,透水和不透水可以认为是2种理想化的边界条件,经典固结理论采用理想化的边界条件,对于固结现象的描述是合理的,所得的相关解析解也已为实际工况和室内试验所验证,对于经典理论的修正和补充,也一直是土力学理论研究的一个方向。本文涉及的所谓连续排水边界条件,是基于使边界条件更符合实际工况这一目的,在不违背Terzaghi固结理论精髓的前提下所做的理论修正方面的研究。其思路基于如下假设:从极短的时间上看,固结边界条件可以认为是不排水,而随着固结时间的延长,又可以认为是排水的。因此,从整体上看,排水边界条件应该和时间有关联,目前所定义的排水和不排水边界条件似乎只是实际情况的上、下限。为此,黄文熙[9]提出过一种半透水边界,但由于解答太深奥和复杂,在实际中使用较少[10-11]。梅国雄等[12-13]基于上述思路对相应的一维固结方程给出初步的理论解答,本文主要是为验证相关的理论解答,基于连续排水边界下Terzaghi固结理论,结合自主开发的连续排水边界子程序,利用ABAQUS有限元分析平台,将得到的数值模拟结果分别与经典的Terzaghi一维固结和连续排水边界下Terzaghi一维固结的解析解以及双层地基一维固结解析解进行对比分析,从而验证连续排水边界理论及其有限元子程序的正确性,并将连续排水边界引入成层地基的一维固结问题,进而讨论该边界条件分别对不同弹性模量、渗透系数和泊松比分布的成层地基一维固结的影响。
1 连续排水边界下Terzaghi固结方程
1.1 连续排水边界的提出
从透水到不透水的连续排水边界条件为:
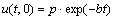 (1)
(1)
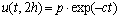 (2)
(2)
其中:u(t,0)为顶部边界t时刻的孔压;u(t, 2h)为底部边界t时刻的孔压,任意深度的土层孔压是关于时间的指数函数,其孔压在顶部和底部边界与时间的指数关系能大体反映土体固结过程的总体趋势;p为边界的初始条件即外荷载条件;b和c是反映边界排水性状的参数,与边界上下土体材料性质有关,其值可通过试验模拟或工程实测反演得出,且b≥0,c≥0。
由式(1)和(2)可知该边界条件具有如下特点:以其中顶部边界条件为例,当t=0时,u(0, 0)=p,符合边界的初始条件即外荷载刚加载的情况;随着固结时间t的增长,u(t, 0)逐渐减小,当t→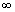 时,u(
时,u(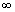 , 0)=0,满足时间无限长、孔压消散完成的基本规律。在式(1)或(2)中,当反映边界排水性状的参数b或者c较小时,可近似描述不排水边界条件;当b→
, 0)=0,满足时间无限长、孔压消散完成的基本规律。在式(1)或(2)中,当反映边界排水性状的参数b或者c较小时,可近似描述不排水边界条件;当b→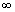 或者c→
或者c→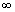 时,u(0, 0)→0,可描述典型的排水边界条件。从上面的分析可知,典型的排水边界条件和近似描述的不排水边界条件是式(1)或式(2)的上、下限,而介于此上下限之间的不同程度的透水边界条件,也可由式(1)或式(2)较好地描述。
时,u(0, 0)→0,可描述典型的排水边界条件。从上面的分析可知,典型的排水边界条件和近似描述的不排水边界条件是式(1)或式(2)的上、下限,而介于此上下限之间的不同程度的透水边界条件,也可由式(1)或式(2)较好地描述。
1.2 连续排水边界下Terzaghi固结方程解答形式
对Terzaghi一维固结方程的边界条件进行修正[12]:
固结方程为
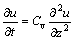 (0≤z≤2h) (3)
(0≤z≤2h) (3)
初始条件为
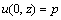 (4)
(4)
边界条件为
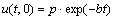 (5)
(5)
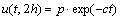 (6)
(6)
式中:Cv为土的竖向固结系数(m2/d);h为地基土层最大竖向排水距离,h=H/2。
这是一个非齐次边界方程,在求解过程中假设荷载是1次施加,且为瞬间施加,得出连续排水边界下Terzaghi一维固结方程的解为
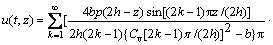

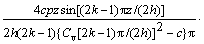
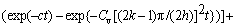
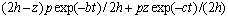 (7)
(7)
连续排水边界下Terzaghi固结方程得到的固结度解答为:
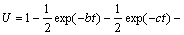
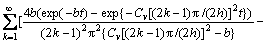
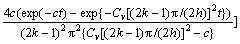 (8)
(8)
从式(7)和(8)可知,连续排水边界下Terzaghi 固结方程得到的解不仅和时间、固结系数、排水距离有关,还和边界条件中给出的参数b和c有关。
2 数值计算与单层地基的对比分析
运用有限元程序ABAQUS以及自行开发的子程序对连续排水边界下均质地基一维固结问题进行数值模拟,再将计算结果分别与经典的Terzaghi一维固结和连续排水边界下Terzaghi一维固结解析公式的结果进行对比分析后,将连续排水边界引入双层地基的一维固结问题进行对比分析。
2.1 程序编制
为和连续排水边界下Terzaghi一维固结理论的条件相对应,首先研究均质地基,计算模型如图1所示。模型高度取10 m,土层的初始孔隙比为1.5,土体表面1次瞬时施加均布荷载p=100 kPa。土层为单一的软弱土层,土体取为线弹性体,弹性模量E=10 MPa,泊松比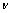 =0.3,渗透系数k=0.007 4 m/d,固结系数Cv=10 m2/d,采用四节点四面体单元和Standard标准模块中的Soil分析步进行分析,利用ABAQUS自定义边界条件子程序DISP接口对土体顶面和底面引入自定义连续排水边界条件[14]。
=0.3,渗透系数k=0.007 4 m/d,固结系数Cv=10 m2/d,采用四节点四面体单元和Standard标准模块中的Soil分析步进行分析,利用ABAQUS自定义边界条件子程序DISP接口对土体顶面和底面引入自定义连续排水边界条件[14]。
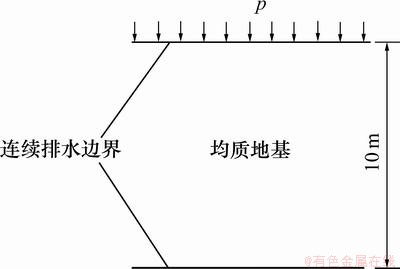
图1 计算模型
Fig.1 Calculation model
边界子程序编程思路如下:在自定义边界子程序中引入孔压、时间、竖向坐标、荷载和上下边界参数b和c共6个变量。首先,固定土体顶面和底面边界的竖向坐标和表面荷载;然后,在该边界处定义孔压随时间和参数b和c变化的指数关系见式(5)和(6)。随着固结时间增量步的输出,边界处的孔压便会随着时间而发生改变,调节参数b和c便可得到不同透水性边界的连续解。
2.2 计算结果与经典Terzaghi一维固结的比较
图2所示为连续排水边界退化为一维Terzaghi固结单面和双面排水边界并同经典的一维Terzaghi固结结果的对比。Tv是时间因子。单面排水是顶面排水、底面不排水,近似于b取值较大,c取值较小的情况。从图2可见:当排水边界参数b=c=15和b=15,c=0.2时,沉降曲线分别同经典的一维Terzaghi双面排水和单面排水曲线基本吻合了。这说明本例中当边界参数b或c等于15时,不妨将该边界视为Terzaghi固结中的排水边界;当边界参数b或者c等于0.2时,不妨将该边界视为Terzaghi固结中的不排水边界。这进一步证明这种连续排水边界退化为经典Terzaghi固结排水边界的可行性,是一种较通用的排水边界条件。
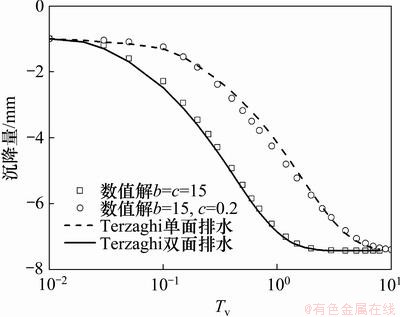
图2 本文方法与经典太沙基一维固结的比较
Fig.2 Comparison between results of present method and Terzaghi’s consolidation theory
上述结果表明:参数b和c的取值对于近似描述一维Terzaghi固结中排水和不排水边界是有范围的,本例中当参数b或c介于0.2到15之间时,可近似描述不同程度的透水边界;考虑到对主要分析区域的计算结果相差很小,不妨认为当参数b或c等于15时,可近似描述排水边界;当参数b或c等于0.2时,可近似描述不排水边界。事实上,不同土体边界参数的范围并不是一致的。从解析式(7)和式(8)可知:边界参数b和c的取值与固结系数、排水距离等均有关,本例中的参数b和c介于0.2到15之间仅是土体其他参数均固定情况下的一种特例。
2.3 计算结果与连续排水边界下Terzaghi一维固结解析解的比较
图3所示为不同时间段土体固结度(Ut)的变化曲线。从图3可见:当边界参数b和c越大时,土体排水速度和固结速度越快,边界排水性越好;当参数b和c越小时,土体排水速度和固结速度越慢,边界排水性越差。传统固结理论的解是不具有连续性的,本文通过调整边界参数b和c可近似模拟实际土层的排水特性,得出透水到不透水边界之间的连续解,从而弥补Terzaghi固结理论只能考虑透水和不透水这2种极端情况的不足。图3中有限元分析结果与解析公式计算值较吻合,这进一步验证了用ABAQUS有限元软件模拟这种连续排水边界方法的正确性。
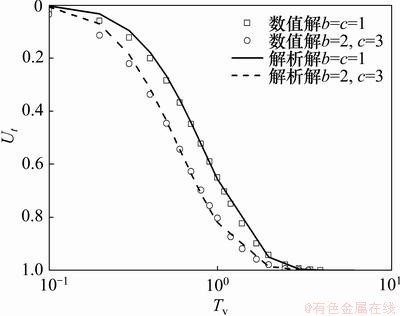
图3 本文方法与连续排水边界下Terzaghi一维固结解析解的比较
Fig.3 Comparison between results of present method and analytical solutions of Terzaghi’s one-dimensional consolidation equation with continuous drainage boundaries
3 数值计算与双层地基的对比分析
运用有限元程序ABAQUS以及自行开发的子程序对连续排水边界下双层地基一维固结问题进行数值模拟,将计算结果与文献[15]中的双层地基一维固结解析公式的结果进行对比分析,再将连续排水边界引入成层地基的一维固结问题进行研究。
3.1 程序编制
计算模型如图4所示。模型高度取10 m,各土层厚度h1=h2=5 m,土层的初始孔隙比为1.5,土体表面1次瞬时施加均布荷载p=100 kPa。土体取为线弹性体,泊松比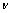 =0.3,弹性模量E1=E2=10 MPa,渗透系数kv1= kv2=0.007 4 m/d,同样利用ABAQUS自定义边界条件子程序DISP接口对土体顶面和底面引入自定义连续排水边界条件,边界子程序编程思路与前面一致。
=0.3,弹性模量E1=E2=10 MPa,渗透系数kv1= kv2=0.007 4 m/d,同样利用ABAQUS自定义边界条件子程序DISP接口对土体顶面和底面引入自定义连续排水边界条件,边界子程序编程思路与前面一致。
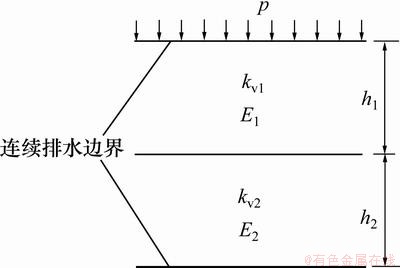
图4 计算模型
Fig.4 Calculation model
3.2 计算结果与双层地基二维固结解析解的对比
图5所示为双层地基一维固结单面排水按沉降定义的平均固结度随时间的变化曲线。从图5可见:当边界参数b=15,c=0.1时,有限元分析结果与文献[15]中解析公式计算值基本吻合,这初步验证了用ABAQUS有限元软件模拟成层地基方法的正确性。
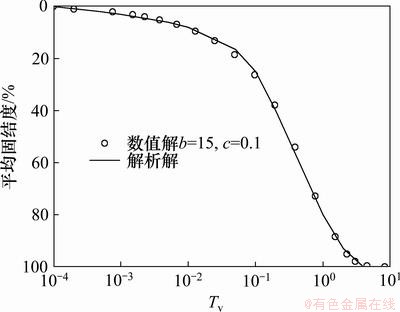
图5 本文方法与双层地基一维固结解析解的比较
Fig.5 Comparison between results of present method and analytical solutions of one-dimensional consolidation for double-layered ground
通过验证ABAQUS有限元软件模拟这种连续排水边界方法在单层和双层地基中的正确性,基于数值模拟方法在理论上可以分层划分计算实际工程中常见的成层地基,对于实际工程中的边界参数b和c的取值可通过试验模拟或工程实测反演得出,因此,将该数值分析方法引入成层地基进行研究。
4 连续排水边界下成层地基一维固结问题的有限元分析
4.1 计算模型
上述研究模拟是基于双层地基,而实际上土层都是成层土,运用有限元程序ABAQUS以及自行开发的子程序,采用变化弹性模量、渗透系数和泊松比的方法对连续排水边界下成层地基一维固结问题进行有限元分析[16],计算模型均取如图6所示。
4.2 连续排水边界下弹性模量对成层地基固结的影响
土体计算参数如表1所示。γ为土的重度;Es为弹性模量。分4种土层分布的情况进行计算比较:(1) 上硬下软,即①和②层土为B类土,③层土为A类土;(2) 上软下硬,即①和②层土为A类土,③层土为B类土;(3) 中间夹硬土层,即①和③层为A类土,②层为B类土;(4) 中间夹软土层,即①和③层为B类土,②层为A类土。
图7所示为Tv=0.2,参数b和c取不同值时不同土层分布情况下孔压沿深度的变化曲线。从图7可见:与单一的土层相比,不管边界参数b和c是否相等,成层地基中的孔压都不关于z=h对称,不同土层的曲线陡缓不一。4种情况在土层的软硬交界处孔压均无明显的拐点,在硬土层中孔压曲线较在软土层中显得平缓,孔压的最大值均出现在软土层中;随着边界参数b和c的不断减小,各土层曲线逐渐趋于平缓。这是边界处透水性能影响不同土层孔压的消散所引起的。图7(c)中不同边界参数下的土体内部孔压相差比图7(a),(b)和(d)中的小,这说明对于土体内部孔压,边界参数b和c的变化对夹有局部硬层的情况比其他3种情况影响要小。
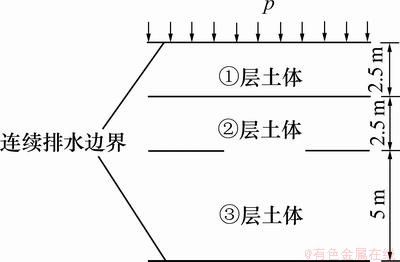
图6 计算模型
Fig.6 Calculation model
表1 土体物理力学参数
Table 1 Parameters of soil properties
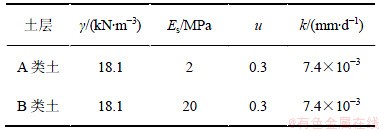

图7 变参数下不同土层的孔压分布曲线
Fig.7 Pore pressure distribution curve of different soils under varying parameters
图8所示为在不同土层分布情况下Tv=0.5时各土层竖向位移沿深度的分布。在经典Terzaghi固结的单一土层中,土层的竖向位移沿深度分布的曲线是光滑的,而图8中的4种情况在土层的软硬交界处竖向位移均有明显的拐点,且软土层竖向位移大,硬土层竖向位移小,这较符合工程实际[17]。当排水边界参数b=c=15时,4种情况下各土层竖向位移均达到最大值。当排水边界参数相同时,图8(c)中的竖向位移均比图8(a),(b)和(d)中的大,这说明在排水边界参数相同时,夹有局部硬层的情况要比其他3种情况更不利。图8(d)中不同边界参数下的土体内部竖向位移相差最大仅为2 mm左右且均较图8(a),8(b)和8(c)中的小,这说明对于土体内部竖向位移,边界参数b和c的变化对局部夹软土层的情况比其他3种情况的影响要小。
4.3 渗透系数对成层地基固结的影响
在一般情况下,渗透系数大于1 m/d的土层可认为是透水性强的土层,而渗透系数小于0.001 m/d的土层可认为是透水性弱的土层。对渗透系数的影响进行分析,同样分4种土层分布的情况进行计算比较,土体计算参数如表2所示:(1) 上部为透水性强下部为透水性弱,即①和②层土为C类土,③层土为D类土;(2) 上部为透水性弱下部为透水性强,即①和②层土为D类土,③层土为C类土;(3) 中间夹透水性弱层,即①和③层为C类土,②层为D类土;(4) 中间夹透水性强层,即①和③层为D类土,②层为C类土。
图9和图10所示分别为不同土层分布情况下不同边界参数土层按沉降定义和按平均有效应力定义的地基总平均固结度随时间的变化曲线[18]。从图9可见:在排水边界参数相同时图9(c)的平均固结度变化均比图9(a),(b)和(d)中的要快,而图9(d)的平均固结度变化均比图9(a),(b)和(c)中的要慢,这说明在排水边界参数相同时,夹有局部透水性弱层的情况比其他3种情况的固结速度要快,而夹有局部透水性强层的情况比其他3种情况的固结速度要慢。图9(d)中随着参数b和c的变化,平均固结度的相差均比图9(a),(b)和(c)的要小,这说明参数b和c的变化对局部夹透水性强层较其他3种情况影响要小。从图10中同样可得到类似的结论。
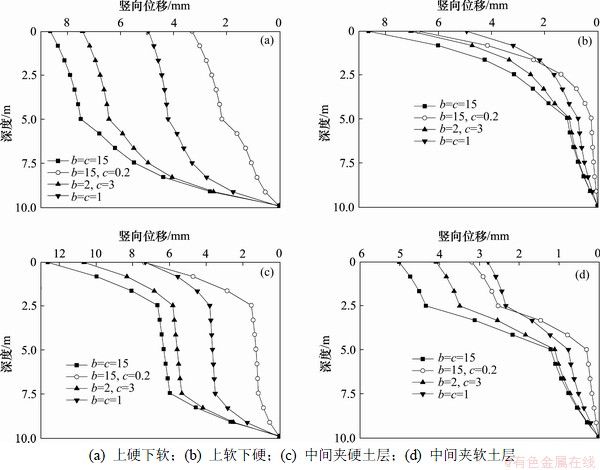
图8 变参数下不同土层的竖向位移曲线
Fig.8 Vertical displacement curves of different soils under varying parameters
表2 土体物理力学参数
Table 2 Parameters of soil properties

4.4 连续排水边界对不同泊松比分布成层地基的影响
连续边界条件对于泊松比的影响比较简单,这里仅取1种特例说明。取泊松比沿深度逐渐变大的情况进行计算,土体计算参数见表3:①层土为E类土;②层土为F类土;③层土为G类土。
表3 土体物理力学参数
Table 3 Parameters of soil properties
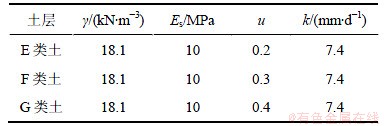
图11所示为Tv=0.5时土体竖向位移沿深度的变化曲线。从图11可见:在土层的交界处竖向位移均无明显的拐点,在不同边界参数下土体竖向位移最大相差仅2 mm左右,即在边界参数b和c的变化下各曲线竖向位移相差很小。对于泊松比沿深度逐渐变大的其他类似模型,也可以得到相同的结论。这可能是由于泊松比的影响很小,从而排水边界参数b和c的变化对不同泊松比分布的土层影响很小。
通过对连续排水边界下不同土层分布情况的弹性模量、渗透系数和泊松比的研究可知:在一定范围内当参数b和c越大时,边界透水性越好,各土层孔压消散的越快,各层土体固结和沉降也越快;当参数b和c越小时,边界透水性越差,各土层孔压消散得越慢,各层土体固结和沉降也越慢。
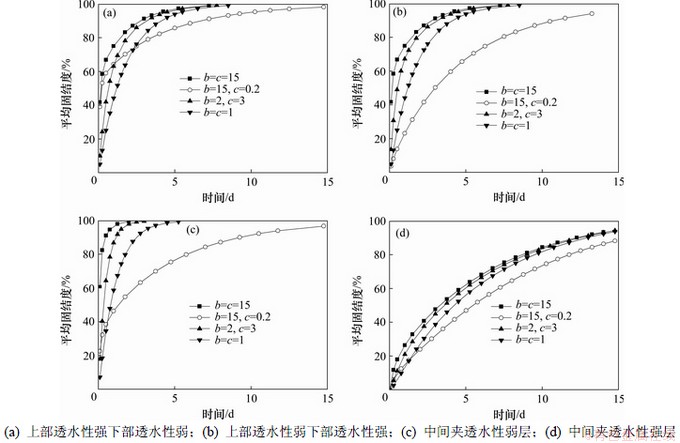
图9 变参数下按沉降定义的平均固结度随时间变化曲线
Fig.9 Relationship between consolidation degree and time defined by settlement under varying parameters
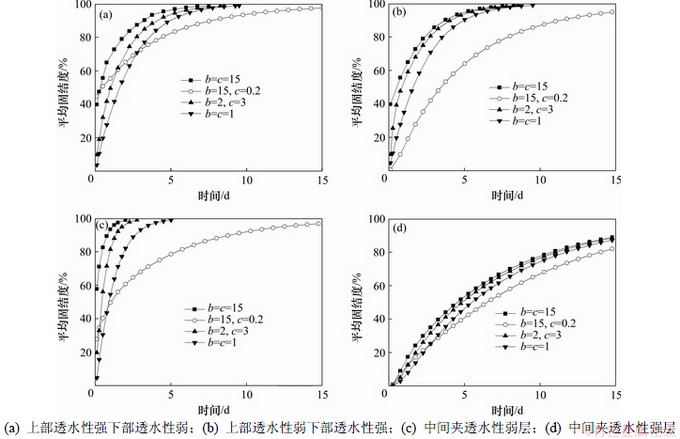
图10 变参数下按平均有效应力定义的平均固结度随时间变化曲线
Fig.10 Relationship between consolidation degree and time defined by effective stress under varying parameters
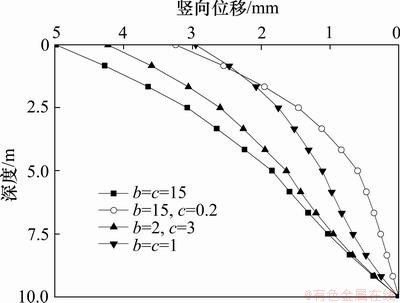
图11 变参数下不同土层的竖向位移曲线
Fig.11 Vertical displacement curve of different soils under varying parameters
5 结论
(1) 通过自行编制的边界条件子程序模拟单层地基中从连续排水边界退化到经典的一维Terzaghi固结排水边界,证明这种连续排水边界退化到经典Terzaghi固结排水边界的可行性,是一种较通用的排水边界条件。
(2) 对连续排水边界下一维Terzaghi固结的数值模拟和解析解进行对比分析得出两者的结果基本吻合;对连续排水边界下双层地基进行数值模拟并与双层地基下一维固结解析解进行对比,验证了连续边界条件理论的合理性,以及使用ABAQUS有限元软件模拟这种连续排水边界方法和成层地基方法的正确性。
(3) 通过调整边界参数b和c可实现模拟实际土层从透水到不透水的不同透水性边界的排水特性并得出连续解,从而弥补Terzaghi固结理论只能考虑透水和不透水这2种极端情况的不足。
(4) 采用变化弹性模量、渗透系数和泊松比的方法对连续排水边界下成层地基一维固结问题进行数值分析,得到较符合工程实际的结果。从分析结果中可以看出:连续排水边界条件能较好地模拟接近实际情况下的工程工况。
由于固结问题的复杂性,如何在弹性模型的基础上更好地反映土体复杂的固结行为,有待进一步研究。
参考文献:
[1] Terzaghi K. Erdbaumechanik and bodenphysikalischer grundlage[M]. Lpz Deuticke, 1925.
[2] Redulic L. Porenziffer and porenwasserdruck in tonen[M]. Bauingenieur, 1936(7): 51-53.
[3] Biot M A. General theory of three-dimensional consolidation [J]. Journal of Applied Physics, 1941(12): 155-167.
[4] Biot M A. Consolidation settlement under a rectangular load distribution[J]. Journal of Applied Physics, 1941, 12(12): 426-430.
[5] Mc namee, Gibson R E. Plan strain and axially symmetric problems of the consolidation of a semi-infinite clay stratum[J]. Journal of Mechanical Applied Mathematics, 1960, 1(2): 124-135.
[6] Gibson R E, Schiffman R L, Pu S L. Plan strain and axially symmetric consolidation of a clay layer on a smooth impervious base[J]. Journal of Mechanical Applied Mathematics, 1970, 23(4): 256-264.
[7] 谢康和, 郑 辉, Leo C J. 软黏土一维非线性大应变固结解析理论[J]. 岩土工程学报, 2002, 24(6): 680-684.
XIE Kanghe, ZHENG Hui, Leo C J. An analytical theory for nonlinear large strain consolidation of soft clay[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(6): 680-684.
[8] 李冰河, 谢康和, 应宏伟, 等. 软黏土非线性一维大应变固结分析[J]. 岩土工程学报, 2000, 22(3): 368-370.
LI Binghe, XIE Kanghe, YING Hongwei, et al. Analys is of one dimensional nonlinear large strain consolidation of soft clay[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(3): 368-370.
[9] 黄文熙. 水坠坝的固结理论及其应用[J]. 水利学报, 1982(9): 13-23.
HUANG Wenxi. Application of consolidation theory to earth dams built by sluicing-siltation method[J]. Journal of Hydraulic Engineering, 1982(9): 13-23.
[10] 胡凌华, 谢康和. 成层地基半透水边界一维固结分析[J]. 科技通报, 2005, 21(3): 321-326.
HU Linghua, XIE Kanghe. On one dimensional consolidation behavior of layered soil with partial drainage boundaries[J]. Bulletin of Science and Technology, 2005, 21(3): 321-326.
[11] 谢康和. 层状土半透水边界一维固结分析[J]. 浙江大学学报, 1996, 30(5): 567-575.
XIE Kanghe. One dimensional consolidation analysis of layered soils with impeded boundaries[J]. Journal of Zhejiang University, 1996, 30(5): 567-575.
[12] 梅国雄, 夏君, 梅岭. 基于不对称连续排水边界的太沙基一维固结方程及其解答[J]. 岩土工程学报, 2011, 33(1): 28-31.
MEI Guoxiong, XIA Jun, MEI Ling. Terzaghi’s one- dimensional consolidation equation and its solution based on asymmetric continuous drainage boundaries[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 28-31.
[13] 郑昱, 梅国雄, 梅岭. 广义连续排水边界在一维固结问题中的应用[J]. 南京工业大学学报, 2010, 32(6): 55-58.
ZHENG Yu, MEI Guoxiong, MEI Ling. Generalized continuous drainage boundaries applied in one dimensional consolidation theory[J]. Journal of Nanjing University of Technology, 2010, 32(6): 55-58.
[14] 费康, 刘汉龙. 边界面模型在ABAQUS的开发应用[J]. 解放军理工大学学报, 2009, 10(5): 447-451.
FEI Kang, LIU Hanlong. Implementation and application of bounding surface model in ABAQUS[J]. Journal of PLA University of Science and Technology, 2009, 10(5): 447-451.
[15] 谢康和. 双层地基一维固结与应用[J]. 岩土工程学报, 1994(5): 25-35.
XIE Kanghe. Theory of one dimensional consolidation of double-layered ground and its applications[J]. Chinese Journal of Geotechnical Engineering, 1994(5): 25-35.
[16] 徐长节, 蔡袁强, 吴世明. 任意荷载下成层弹性地基的一维固结[J]. 土木工程学报, 1999, 32(4): 57-63.
XU Changjie, CAI Yuanqiang, WU Shiming. One dimensional consolidation of layered elastic soils under arbitrary loading[J]. China Civil Engineering Journal, 1999, 32(4): 57-63.
[17] 鹿群, 龚晓南, 崔武文, 等. 饱和成层地基中静压单桩挤土效应的有限元模拟[J]. 岩土力学, 2008, 29(11): 3017-3020.
LU Qun, GONG Xiaonan, CUI Wenwu, et al. Squeezing effects of jacked pile in layered soil[J]. Rock and Soil Mechanics, 2008, 29(11): 3017-3020.
[18] 罗勇, 龚晓南, 连峰. 成层地基固结性状中不同定义平均固结度研究分析[J]. 科技通报, 2006, 22(6): 813-816.
LUO Yong, GONG Xiaonan, LIAN Feng. Comparable analysis of different definitions of average degree of consolidation of layered soils[J]. Bulletin of Science and Technology, 2006, 22(6): 813-816.
(编辑 邓履翔)
收稿日期:2012-01-09;修回日期:2012-03-19
基金项目:国家自然科学基金资助项目(50608038)
通信作者:梅国雄(1975-),男,湖北黄梅人,教授,博士生导师,从事固结理论和土体基本性质等研究;电话:025-83587715;E-mail: meigx@163.com