J. Cent. South Univ. (2012) 19: 2572-2577
DOI: 10.1007/s11771-012-1312-y
A model and simulation of cathode flooding and drying on unsteady proton exchange membrane fuel cell
A. Bakhtiar1, KIM Young-Bok2, YOU Jin-Kwang3, YOON Jung-In 1, CHOI Kwang-Hwan1
1. Refrigeration and Air-Conditioning Engineering, Pukyong National University, Busan, Korea;
2. Department of Automotive, Dong-Pusan Collage University, Korea;
3. Department of Mechanical Engineering, Pukyong National University, Busan, Korea
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: A water balance has a significant impact on the overall system performance in proton exchange membrane fuel cell. An actual fuel cell application has a dynamic electrical load which means also dynamic electrical current. Therefore, since this electrical current is known, the water production from the fuel cell reaction is also able to be predicted. As long as the fuel cell water transportation model is provided, the present liquid water inside the porous medium is also able to be modeled. A model of the liquid water saturation level in a fuel cell in unsteady load condition was proposed. This model is a series of the water transportation model of water saturation level for the final output of proton exchange membrane (PEM) fuel cell to predict the flooding or drying of PEM fuel cell. The simulation of vehicle fuel cell in different dynamic load profiles and different inlet air conditions was done using this model. The simulation result shows that PEM fuel cell with different dynamic load profiles has different liquid water saturation level profiles. This means that a dynamic load fuel cell requires also a dynamic input air humidification.
Key words: model; simulation; flooding; unsteady condition; fuel cell
1 Introduction
Replacement of the fossil fuels with green energy resources plays a fundamental role in solving the energy crisis and global warming issues. Automobiles are sources of considerable pollution at the global level, including a significant fraction of the total greenhouse gas emissions. Using fuel cell in automobiles will replace the automobile energy source from fossil fuel into hydrogen that is a renewable and clean energy. Among types of fuel cells, proton exchange membrane (PEM) fuel cell is the most promising candidate, especially for automobile applications, because of its high-energy density at low operating temperatures, quick start-up and zero emission [l-4].
In an unsteady PEM fuel cell application such as vehicle, the fuel cell electric current is dynamic and depended on the vehicle’s power load. The fuel cell water production is the function of the electric current. Therefore, if the fuel cell water transportation can be calculated, the liquid water saturation level should be able to be predicted. This should be used for an important control reference in the water management system.
There are many reports trying to model the water transportation inside the PEM fuel cell, but most of them are in steady condition [5-6]. These water transportation models have been used by many applicants to control the operating condition of fuel cell in order to get the water balance. To know that the fuel cell is flooding or not, they used physical indicators instead of the amount of liquid water inside the pores because measuring the actual amount of the liquid water in the dynamic condition is very difficult. Hence, in this work, a liquid water saturation level model of the PEM fuel cell is proposed to predict the flooding or drying condition for unsteady state fuel cell application.
2 Proposed model
Based on the principles of water balance, an analytical model is developed to describe PEM fuel cell. The specific assumptions of the present model are: 1) The fuel cell is treated as a lumped system with a uniform temperature; 2) Incompressible and ideal gas mixture; 3) Isotropic and homogeneous gas diffusion layer (GDL), cathode catalyst layer (CCL) and membrane; 4) Negligible voltage loss due to electronic resistances.
2.1 Vehicle power model
The vehicle power model used in this simulation is given by Eqs. (1)-(4). Wroll, Wreeist, Wkinetic are the powers absorbed by rolling resistance, air resistance and kinetic power, respectively [7]:
Wroll=mgcrf|v| (1)
Wresist=1/2ρa|v|3cdA (2)
 (3)
(3)
Wtotal=Wroll+Wresist+Wkinetic (4)
2.2 Water balance
The water balance is the balance between the GDL water addition and removal as simplified in Fig. 1. The water additions are obtained from the fuel cell reaction (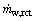 ) and input air (
) and input air (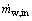 ). The water removals are obtained from the evaporation and convection process. If the water addition rate is higher than its removal, the water difference will be accumulated and result in a flooding.
). The water removals are obtained from the evaporation and convection process. If the water addition rate is higher than its removal, the water difference will be accumulated and result in a flooding.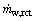 is expressed as the total water production from oxygen reduction reaction (ORR) and electro osmotic drag as given in Eq. (5) [ HYPERLINK \l "Len07" 8 ]. The water addition from the input air is obtained from its humidity and given in Eq. (6) 9]�:
is expressed as the total water production from oxygen reduction reaction (ORR) and electro osmotic drag as given in Eq. (5) [ HYPERLINK \l "Len07" 8 ]. The water addition from the input air is obtained from its humidity and given in Eq. (6) 9]�:
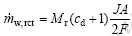
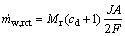 (5)
(5)
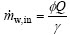
 (6)
(6)
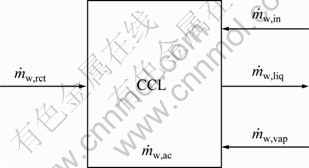
Fig. 1 Water mass conservation
2.3 Water addition effect
The output water can be done in two phases as shown in Fig. 2. The mass flow rate of the saturated air is given by Eq. (7). Since the water addition is not sufficient to make the air stream become fully saturated, this water addition is fully removed in vapor phase. The available space of air stream to be occupied with more water additions is determined by Eq. (8):
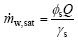
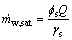 (7)
(7)
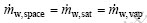
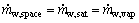 (8)
(8)
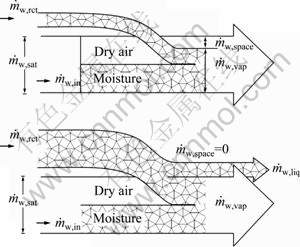
Fig. 2 Water output phase
As long as the water output is saturated, the space for the output air to hold extra water is zero and the liquid water production is determined by Eq. (9):
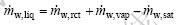
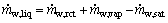 (9)
(9)
The water liquid saturation level (s) is defined as the volume fraction of the total void space of porous media occupied by the liquid phase [ HYPERLINK \l "S1" 10 ]. The change of s after receiving liquid water addition is given by Eq. (11) and Vp is the GDL pore void volume which is depended on its porosity:
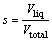 (10)
(10)
 (11)
(11)
2.4 Capillary transport
The capillary transport is the dominant transport process to remove water from flooded GDLs [11-12]. The concept of relative permeability (krk) defines the ratio of intrinsic permeability of a phase k at a given saturation level to the total intrinsic permeability of the porous medium. The capillary pressure between two phases is expressed in Eq. (13) and J(s) is the Leverett J-function and is given by Eq. (14) [5, 13-15]:
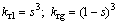 (12)
(12)
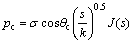 (13)
(13)
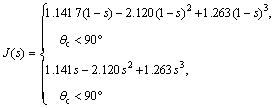 (14)
(14)
For a hydrophilic medium, the wetting phase is the liquid phase. The mass of liquid water is equal to the amount of liquid water generation rate in the cathode CCL due to over-saturated condition. Therefore, the mass flow rate of transported water driven by capillary pressure is given by [11]
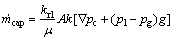 (15)
(15)
Leverett J-function has followed the assumption that the gas-phase pressure remains constant throughout the GDL and is equal to the ambient pressure in the cathode gas channel. Furthermore, due to very small dimensional geometry of PEM fuel cell, the gravity effect can be neglected. Substituting Eq. (13) into Eq. (15) results in Eq. (16). And for hydrophobic media, the Laverett J- function is given by Eq. (17):
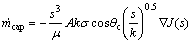 (16)
(16)
J(s)=1.417s-2.120s2+1.26s3 (17)
Combining Eq. (16) and Eq. (17) yields
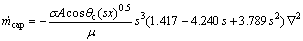 (18)
(18)
Considering the one-dimensional transport of liquid water only in the trough plane direction, Eq. (18) reduces to an ordinary differential equation, which can be solved analytically. For hydrophobic GDL, Eq. (19) is used:
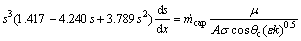 (19)
(19)
Assuming that the gradient of s along the GDL is linear, the maximum value is obtained at the contact area between GDL and CCL. The gradient of s along the GDL, the mass flow rate of the capillary water transported and the liquid saturation change are given by Eqs. (20)-(22), respectively:
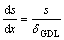 (20)
(20)
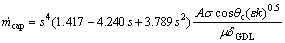 (21)
(21)
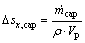 (22)
(22)
2.5 Evaporation process
The model of liquid saturation used in this work is a cubic, as shown in Fig. 3. Total volume of the cube is a3 with total surface area of 6a2. If there is a liquid phase present in control volume with liquid saturation s, the surface area of liquid becomes (4s+2)a2. Using this saturation cube model, the water evaporation rate of fuel cell is given by Eq. (23) and the evaporated water is limited by the available space of the water stream due to the saturation pressure:
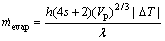 (23)
(23)
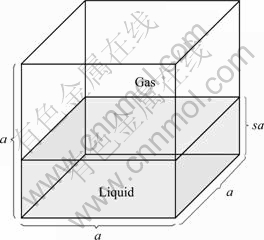
Fig. 3 Phase saturation cube model
Since air stream is fully saturated, evaporation will never happen because  is zero. This is depended on the factors that support the evaporation process such as temperature and pressure. The liquid saturation due to evaporation process is given by Eq. (24). And the final liquid saturation level change from water additions and removals are given by Eq. (25):
is zero. This is depended on the factors that support the evaporation process such as temperature and pressure. The liquid saturation due to evaporation process is given by Eq. (24). And the final liquid saturation level change from water additions and removals are given by Eq. (25):
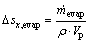 (24)
(24)
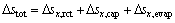 (25)
(25)
3 Simulation
The parameters used in this simulation are given in Table 1. The dynamic loads profiles are taken from driving cycles based on light duty vehicles driving schedule by several standards. There are three driving cycles used in this simulation [16]. First is New York City cycle (NYCC). This cycle is released by the Environmental Protection Agency (EPA) of United States and used for simulating low speed city driving. Second driving cycle is extra urban driving cycle (EUDC) that is released by Economic Commission for Europe Dynamometer Operating Cycles (ECEDO) and used for simulating highway driving conditions with the maximum speed of the EUDC cycle of 120 km/h. And the third driving is the Japan 10-15 mode cycles by Japanese Industrial Safety and Health Association (JISHA). This mode is currently used in Japan for emission certification and fuel economy for light duty vehicles. The speed data of the used driving cycle that is taken from Ref. [16] are shown in Fig. 4.
Table 1 Fuel cell simulation parameters
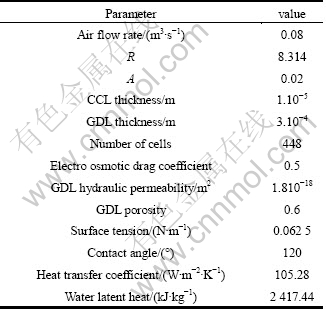
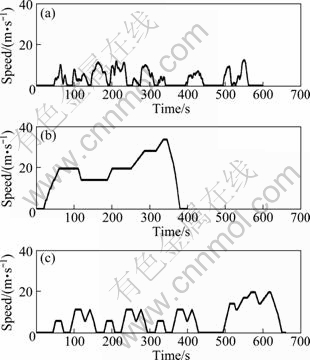
Fig. 4 Driving cycle speed profiles: (a) NYCC; (b) EUDC; (c) JP 10-15
4 Results and discussion
The power requested by the engine is a product of the speed and force. During acceleration, the force is positive. And since the speed is always positive, the power demand is positive and this power demand should be met by the power generation system. During deceleration, the force and hence the power requested is negative. And since this is handled by the braking system, the power requested from the power generation subsystem is zero. Therefore, using power vehicle model as given in Eq. (4), the power demand of the vehicle is shown in Fig. 5. And the current densities of all driving cycles are shown in Fig. 6.
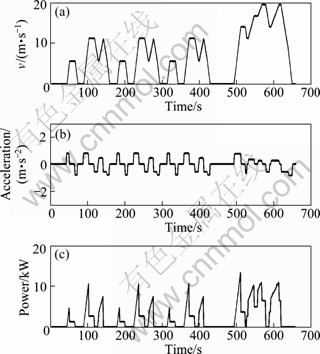
Fig. 5 Sample power profiles of JISHA JP 10-15 mode
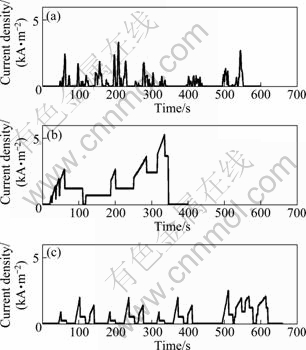
Fig. 6 Current density profiles: (a) NYCC; (b) EUDC; (c) JP 10-15
Simulation is started with low temperature and humidity ratio of the input air. The temperature in this condition is 40 ℃ and the relative humidity is 50%. Hence, the humidity ratio is 23.5 g/kg, as shown in Fig. 7. At low temperature, saturation pressure is low. Therefore, the capability of the air stream to hold water is relatively low. In this condition, the over-saturated air stream tends to occur. As long as the amount of water addition is lower than the saturation amount, the saturated condition will never occur. Flooding phenomenon mostly occurs in all profiles at low temperature, as shown in Fig. 7. EUDC has higher power load than other cycles. Therefore, the received water is higher and EUDC has higher liquid saturation level.
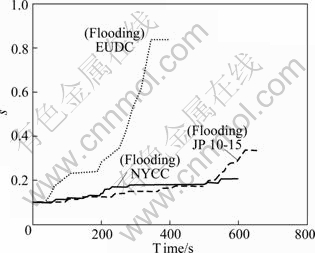
Fig. 7 Saturation level of 40 ℃, 50 % RH and dynamic power
Increasing the temperature of the air input from 40 ℃ to 60 ℃ will decrease the relative humidity from 50% to 18.5% with same humidity ratio of 23.5 g/kg. In this condition, the capability of the air stream to hold moistures is higher than previous condition. Therefore, the low load profiles get dried. In this condition, the capability of the air stream to carry out water is higher than before, but the evaporation rate is also high, therefore, the drying still happens, as shown in Fig. 8.
In order to avoid drying, increasing the humidity ratio becomes the common method. The final simulation condition is done by increasing the humidity ratio of the input air, as shown in Fig. 9. This figure shows the liquid saturation level of fuel cell at 60 ℃ in air with 67.9 g/kg humidity ratio (50% RH). In this condition, the flooding on low load profiles such as NYCC and JP 10-15 can be avoided. And also the over flooding of high load profiles (EUDC) can be reduced. Hence, better water management is reached.

Fig. 8 Saturation level of 60 ℃, 18.5% RH and dynamic power
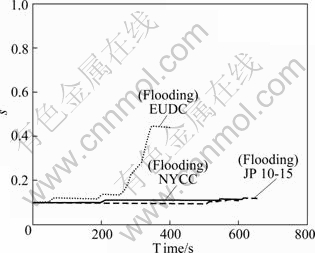
Fig. 9 Saturation level of 60 ℃, 50% RH and dynamic power
5 Conclusions
1) The rate of liquid water accumulation is a vector that has a plus value when the production rate of liquid water is higher than the removal rate of liquid water. Hence, when it is remained for long time, it will produce a flooding. The rate of flooding is depended on the value of water accumulation rate, and higher value of it will perform faster flooding.
2) The simulation is completely done by varying the driving cycles into the vehicle model to get the different dynamic load profiles. And the result shows that to get the water balance, fuel cell with different dynamic load profiles requires also different static conditions of temperature and humidity of air input.
3) The proper conditions of water management parameters are different in every dynamic load profile. Hence, dynamic water management system is required.
Nomenclature

Subscript
References
[1] LI Hui, TANG Yang-hua, WANG Zhen-wei, SHI Zheng, WU Shao-hong, SONG Da-tong, ZHANG Jian-lu, KHALID FATIH, ZHANG Jiu-jun, WANG Hai-jiang, LIU Zhong-sheng, ABOUATALLAH R, MAZZA A. A review of water flooding issues in the proton exchange membrane fuel cell [J]. Journal of Power Sources, 2008, 178(1): 103-117.
[2] KUI J, XIANGUO L. Water transport in polymer electrolyte membrane fuel cells [J]. Progress in Energy and Combustion Science, 2011, 37(3): 221-291.
[3] YONG Tang, YUAN Wei, PAN Min-qiang, LI Zong-tao, CHEN Guo-qing, LI Yong. Experimental investigation of dynamic performance and transient responses of a kW-class PEM fuel cell stack under various load changes [J]. Applied Energy, 2010, 87(4): 1410-1417.
[4] CHEN Ji-xin, ZHOU Biao. Diagnosis of PEM fuel cell stack dynamic behaviors [J]. Journal of Power Sources, 2008, 177(1): 83-95.
[5] DAS P K, LI Xian-guo, LIU Zhong-sheng. Analysis of liquid water transport in cathode catalyst layer of PEM fuel cells [J]. International Journal of Hydrogen Energy, 2010, 35(6): 2403-2416.
[6] HUANG M. Numerical studies of liquid water behaviors in PEM fuel cell cathode considering transport across different porous layers [J]. International Journal of Hydrogen Energy, 2010, 35(11): 5569-5579.
[7] ZENITH F, SKOGESTAD S. Control of the mass and energy dynamics of polybenzimidazole-membrane fuel cells [J]. Journal of Process Control, 2009, 19(3): 415-432.
[8] MAO Leng, WANG Chao-yang. Analysis of cold start in polymer electrolyte fuel cells [J]. Journalof the Electrochem Society B, 2007, 154: 139-146.
[9] ASHRAE. 2007 ASHRAE handbook on HVAC applications [M]. Atlanta: American Society of Heating, Refrigerating and Air-conditioning Engineers, Inc, 2007.
[10] ITO K, ASHIKAGA K, MASUDA H, OSHIMA T, KAKIMOTO Y, SASAKI K. Estimation of flooding in PEMFC gas diffusion layer by differential pressure measurement [J]. Journal of Power Sources, 2008, 175(2): 732-738.
[11] UGUR PASAOGULLARI, WANG C Y. Liquid water transport in gas diffusion layer of polymer electrolyte fuel cells [J]. Journal of the Electrochem Society A, 2004, 154: 399-406.
[12] JU HYUNCHUL. Analyzing the effects of immobile liquidsaturation and spatial wettability variation on liquid water transport in diffusion media of polymer electrolyte fuel cells (PEFCs) [J]. Journal of Power Sources, 2008, 185(1): 55-62.
[13] LEVERETT M C. Capillary behaviour in porous solids [J]. Transactions of the American Institute of Mining and Metallurgical Engineers, 1941, 142: 152-169.
[14] DALASM K H N, KAZUYOSHI F, KEN O. Three-dimensional transient two-phase study of the cathode side of a PEM fuel cell [J]. International Journal of Hydrogen Energy, 2010, 35(9): 4234-4246.
[15] LIANG H, PING C. Capillarypressures in carbon paper gas diffusion layers having hydrophilic and hydrophobic pores [J]. International Journal of Heat and Mass Transfer, 2012, 55: 133-139.
[16] US Environmental Protection Agency. Testing and measuring emissions [EB/OL]. [2012-05-01] http://www.epa.gov/nvfel/testing/ dynamometer.htm
(Edited by YANG Bing)
Received date: 2011-07-19; Accepted date: 2012-05-02
Corresponding author: CHOI Kwang-Hwan; Tel: +82-51-629-6179; E-mail: 1r