J. Cent. South Univ. (2012) 19: 2598-2603
DOI: 10.1007/s11771-012-1316-7
Circle geometric constraint model for open-pit mine ore-matching and its applications
HUANG Jun-xin(黄俊歆)1,2, WANG Li-guan(王李管)1, XIONG Shu-min(熊书敏)1,
XU Shao-you(徐少游)1, TAN Zheng-hua(谭正华)1, WANG Hai-qiao(王海桥)3
1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;
2. Department of Safety and Environment Engineering, Hunan Institute of Technology, Hengyang 421001, China;
3. School of Energy and Safety Engineering, Hunan University of Science and Technology, Xiangtan 411201, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: The circle geometric constraint model (CGCM) was put forward for resolving the open-pit mine ore-matching problems (OMOMP). By adopting the approaches of graph theory, block model of blasted piles was abstracted into a set of nodes and directed edges, which were connected together with other nodes in the range of circle constraints, to describe the mining sequence. Also, the constructing method of CGCM was introduced in detail. The algorithm of CGCM has been realized in the DIMINE system, and applied to a short-term (5 d) program calculation for ore-matching of a cement limestone mine in Hebei Province, China. The applications show that CGCM can well describe the mining sequence of ore blocks and its mining geometric constraints in the process of mining blasted piles. This model, which is applicable for resolving OMOMP under complicated geometric constraints with accurate results, provides effective ways to solve the problems of open-pit ore-matching.
Key words: open-pit mine; block model; blasted-pile mining optimization; linear programming; mixed integer programming (MIP)
1 Introduction
Ore-matching means to match ore with different grades for mixing them evenly. In the process of mining and shipping, ore-matching, based on existing resources and production capacity, which is carried out in accordance with relevant index, helps to ensure the quality of ore, increase mine income and provide ore reasonably [1-2].
In the 15th APCOM (Applied Physics of Condensed Matter) Conference, Germany scholars, WILKE and REIMER, first put forward open-pit short-term planning model by using linear programming. Later, in view of problems of actual management for bauxite mine, WANG and LU proposed the ore-matching optimization model based on 0-1 integer programming; XU and YANG put forward a multi-objective optimization method based on fuzziness. Linear membership model is applied to mirror the features of fuzzy objective, and seven linguistic values are employed to represent preference of fuzziness importance. By adopting this method, two-step ore-matching optimization model was established for coordinating the conflicts between objective functions in multi-objective programming model. Owing to lack of sample data for limestone mine, it is difficult to reflect the real distribution rule of blasted-pile grade, therefore, LIN and LIU proposed the UM model where unascertained rational number is applied in ore-matching optimization. Combined with GIS, GPS and GPRS, GU and WEN set up a open-pit ore-matching management system, which includes open-pit stripping program and transportation scheduling system, forming a set of ore quality control system [3-11].
But all these methods described above adopted the method of manual setting mining sequence and mining range for defining geometric constraints in the mining process. Obviously, the aim of optimizing ore-matching could not be achieved. To resolve the problems of OMOMP by using optimization theory, it is crucial that an accurate and feasible mining geometric constraint model is available. However, there is no such developed geometric constraints model that can be used for solving OMOMP. Therefore, the circle geometric constrains model (CGCM) was put forward in this work, with its effectiveness and feasibility verified in actual projects.
2 Open-pit ore-matching flow
Blasted-pile is divided into several cuboids with the same size, including ore and waste rock, which constitute discrete model, also called as blasted-pile block model. By adopting the methods of ore-body interpretation and geological data analysis, the ore reserves, waste rock amount and net value of each cuboid in the block model can be estimated. The block model after estimation is called value block model. Figure 1 shows the flow chart of open-pit ore-matching.
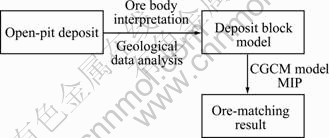
Fig. 1 Flow chart of open-pit mine ore-matching
3 Construction of CGCM model
3.1 Fundamental principles
When mining operation is carried out by using excavator, the mining range is the circular area of excavator, with its rotation center as circle center and its arm length as radius, as shown in Fig. 2. The positive direction of j axis is the mining direction, and the positive direction of i axis is the bench advancing direction. The dimensions of block in i and j directions are wi and wj, respectively. Excavator moves along the mining direction to carry out mining operation. Then CGCM model could be set up based on this principle.
The simple 2D block model in Fig. 2 was adopted to describe the fundamental principle of CGCM model, with its center point representing this block (hereinafter refers as node).
It is necessary to determine the mining direction before setting up CGCM model. For any node N as the starting point, draw a vertical line in the mining direction, with its length equal to arm length (R) of excavator, and the end point is O. Draw a circle, with O as its circle center (coordinate: (io , jo)) and R as radius. Nodes (meet the formula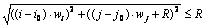 
) in the block model lied in this circle constitute a node set, which must be mined before mining node N, called the CGCM model of node N, as shown in Fig. 2.
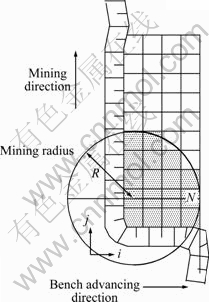
Fig. 2 Blasted-pile block model and CGCM of a single block
3.2 Algorithm to construct CGCM
The coordinate system was set up, as shown in Fig. 3: XY coordinate system is the World Coordinate System, with its value as the real coordinates of nodes; ij coordinate system is the relative coordinate system, with its value as the serial number of blocks in the blasted-pile block model.
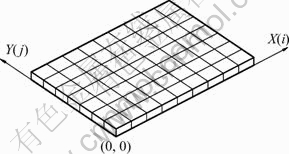
Fig. 3 Coordinate system of blasted-pile block model
Traversing all the nodes in the blasted-pile block model, CGCMs are constructed for each node. Supposing that the coordinate of the current node is (io, jo), and the block model includes max(i) rows and max(j) columns, the algorithm of constructing CGCM of node (io, jo) is described as follows:
Step 1: i=0;
Step 2: j=0;
Step 3: When the coordinate of the current node is (i, j), if it meets the formula 
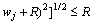, directed edge is adopted to connect node (i0 , j0) with node (i, j), thereby, node (i, j) is added into the CGCM of node (i0, j0). Otherwise, proceed the next step;
Step 4: if j Step 5: if i Figure 4 shows the flow chart of program.
3.3 Objective function of linear programming model
As for a given blasted-pile block model, there are n blasted-piles involved in ore-matching. Suppose that each blasted-pile block is divided into r rows and l columns; Os,ij is decision variable, with its value as 0 or 1, which means the unit block in row-i and column-j in the blasted-pile s is mined or not. Os,ij=1 means mining, while Os,ij=0 means not mining. xs,ij is the ore amount of block in row-i and column-j in the blasted-pile s, and ys,ij is the rock amount of block in row-i and column-j in the blasted-pile s. The mining objective is to maximize the ore amount, therefore, the expression of objective function is [12-14]
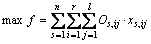(1)
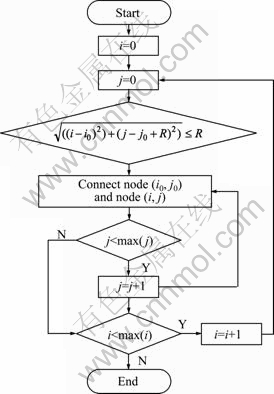
Fig. 4 Flow chart of constructing CGCM
3.4 Constraints of constructing linear programming model
1) Constraints of ore removal amount for each blasted-pile
First of all, each blasted-pile involved in ore-matching must have the ability of ore removal; secondly, the ore removal amount of each blasted-pile is limited by the capacity of mining equipment, and cannot exceed the max mining capacity of qs:
(s=1, 2, …, n) (2)
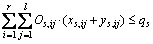(s=1, 2, …, n) (3)
2) Constraints of total amount of ore removal
According to production plan, the total amount of ore removal in the constraint period must meet its production requirement, and not less than minimum output of Qmin, namely:
(4)
3) Constraints of elements grade
The key of ore-matching optimization is to meet the requirement of average grade of each element for balancing ore supply. In different mines, there are lower limits for beneficial element grade or index, and upper limits for some element grade or index which are harmful. Assume that the upper indexes of w elements a1, a2, …, aw are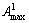 
, 
,…, 
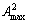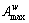, respectively, and lower indexes are 
, 
,…, 
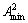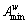, respectively; therefore, constrains of element grade are
(5)
(6)
4) Geometric constraints
According to the method described in Section 2.1.1, take any node N to construct its CGCM. Assume that there are k nodes to be mined firstly in the CGCM of node N; therefore, the expression of geometric constraints model of node N is
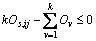
(s=1, 2,…, n; i=1, 2, …, r; j=1, 2, …, l) (7)
where Ov means whether the v-th block in all the k unit blocks within geometric constraints range is mined or not: Ov=1, mining; Ov=0, not mining.
4 Examples
4.1 Creating 3D geological model
The algorithm based on CGCM has been applied in DIMINE digital mine system. Taking a cement limestone mine in Hebei province as example, DIMINE was adopted to create the spatial geological database, digital terrain model (DTM) [15-16], ore-body model and ore grade block model of the mine, as shown in Fig. 5. All these data are foundations for open-pit mine ore-matching.
Fig. 5 Digital model, main ore-body (a) and blasted-piles distribution (b)
The distribution of ore-body is complicated. The main body, which is composed of 11 bedded ore bodies, generally inclines in southwest like a half graben. Inclination of south limb occurs at 310°-345°, with dip angle of 35°-55°; inclination of north limb occurs at about 170°, with dip angle of 32°-75°; inclination of core occurs at 220°-240°, with dip angle of 13°-35°; the overall length of ore-body is 2 000 m, the minimum thickness of ore-body is 11.85 m, and the average thickness is 18.01 m. Thickness and grade of the ore-body vary greatly, and Table 1 gives the specific resource reserves of each ore-body.
Table 1 Table of resources estimation
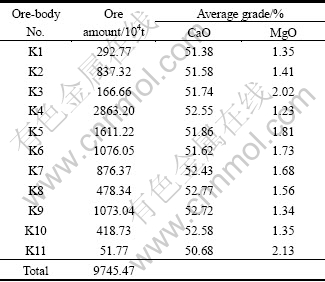
Deposit includes five ore-bodies K4, K5, K6, K7 and K9, and K4 has the largest ore reserves. Choose the dimension of unit block as 3 m×3 m×12 m (12 m is the bench height) to create block model. Three blasted piles to be mined and their grades distribution are shown in Fig. 6, and Table 1 gives their reserves and grade.
Fig. 6 Value block model of each blasted-pile and its grade distribution: (a) Blasted-pile 1; (b) Blasted-pile 2; (c) Blasted-pile 3
4.2 Selection of optimal parameters
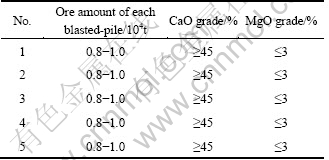
In the process of blasted-pile mining optimization, a program calculation of short-term (5 d) ore-matching was performed based on the actual project and equipments. Table 2 gives the ore amount and grade constraints. Gyration radius of excavator is 15 m, and tolerance of ore amount is 5%.
Table 2 Optimal parameters
4.3 Results analysis
Input the optimal parameters described above into the open-pit ore-matching module of DIMINE software, and the results are shown in Fig. 7 and Table 3.
Fig. 7 Results of open-pit mine ore-matching: (a) Blasted-pile 1; (b) Blasted-pile 2; (c) Blasted-pile 3
Table 3 Ore-matching parameters of each period in each blasted-pile
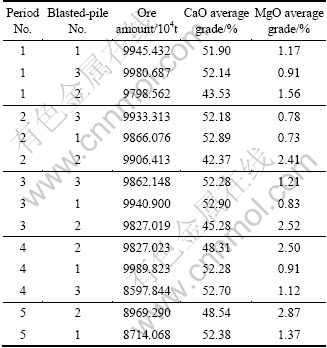
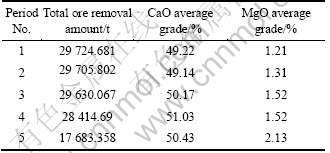
It can be seen from Fig. 6 that, the grades of blast-pile 2 are relatively low, with most of them lower than 45%; while the grades of blast-piles 1 and 3 are relatively high. Therefore, the values of removal ore-amount and average grade of the same Period No. in Table 3 are collected. The results show that, combining the CGCM and MIP algorithm, we have to make a reasonable collocation of ore removal amount of three blast-piles, in order to make a balance in ore grades. All these works meet the demand of balanced and optimized ore removal. Table 4 gives the summarized parameters.
Table 4 Total ore removal amount and its average grades of each period
5 Conclusions
1) A novel geometric constraint model of open-pit ore-matching, circle geometric constraint model (CGCM), is put forward and applied to actual projects. The applications show that CGCM can well describe the mining sequence of ore block and its mining geometric constraints in the process of open-pit ore-matching. This model provides effective ways to solve the problems of open-pit ore-matching.
2) The deficiency of CGCM lies in the fact that it depends on regular 3D block model, and the subdivision degree of block and its size in all directions influence greatly the accuracy of results. However, the complexity of mixed integer programming algorithm is in exponential order, and block is divided into too small sections, which will result in excessive computing. How to construct irregular block model and adjust its block dimension, shape, and subdivision degree in different benches and different sites to accurately simulate working slope angle and mining strip are difficulties and developing directions for setting up open-pit ore-matching model in the future.
References
[1] WANG Qin. Mining science [M]. Beijing: Metallurgy Industry Press, 2007: 344-394. (in Chinese)
[2] SHU Hang. Ore quality balance and control [M]. Beijing: Metallurgical Industry Press, 1994: 39-53. (in Chinese)
[3] YUAN Huai-yu. United dynamic optimization study on the rational beneficiation feed grade [J]. Journal of University of Science and Technology Beijing, 2002, 24(3): 239-242. (in Chinese)
[4] XU Tie-jun, Yang Peng. Application of improved Genetic algorithm in mine ore blending [C]// The 3rd International Symposium on Modern Mining & Safety Technology Proceedings. Fuxin, 2008: 174-180.
[5] HU Qing-huai. A mathematical model study on ore blending in mine production under restrictions [J]. Mining Research and Development, 2002, 22(6): 1-6. (in Chinese)
[6] JANA C, CHATTOPADHYAY R N. Block level energy planning for domestic lighting-A multi-objective fuzzy linear programming approach [J]. Energy, 2004, 29: 1819-1829.
[7] ARENAS M, BILBAO A, RODRIGUEZ M V. Solving a multi-objective possibility problem through compromise programming [J]. European Journal of Operational Research, 2005, 164: 748-758.
[8] GAO Jin-wu, LIU Bao-ding. Fuzzy multilevel programming with a hybrid intelligent algorithm [J]. Computers & Mathematics with Applications, 2005, 49(9/10): 1539-1545.
[9] CHEN L H, TSAI F C. Fuzzy goal programming with different importance and priorities [J]. European Journal of Operational Research, 2001, 133: 548-556.
[10] LIU Bao-ding, LIU Yan-kui. Expected value of fuzzy variable and fuzzy expected value models [J]. IEEE Trans Fuzzy Syst, 2002, 10(4): 445-454.
[11] WANG Bin. Study on optimization for ore blending system of limestone mine in hills [D]. Wuhan: Wuhan University of Science and Technology, 2005: 49-58. (in Chinese)
[12] XU Jiu-jun, LI Jun. Multi-objective decision theory and methodology [M]. Beijing: Tsinghua University Press, 2005: 86-99. (in Chinese)
[13] CHEN Bao-lin. Optimization theory and algorithm [M]. 2nd Ed. Beijing: Tsinghua University Press, 2005: 432-450. (in Chinese)
[14] PANG Bi-jun. Linear programming and stochastic programming [M]. Zhengzhou: Zhengzhou University Press, 2009: 1-16. (in Chinese)
[15] BI Lin, WANG Li-guan, CHEN Jian-hong. Fast triangulation algorithm for polygon regions and implementation [J]. Application Research of Computers, 2008, 25(10): 3030-3033. (in Chinese)
[16] HUANG Jun-xin, WANG Li-guan, BI Lin. The improved geometrical constraint model of open-pit mine boundary optimum and its application [J]. Journal of Chongqing University, 2010, 33(12): 78-83. (in Chinese)
(Edited by YANG Bing)
Foundation item: Project(2011AA060407) supported by the National High Technology Research and Development Program of China; Project(51074073) supported by the National Natural Science Foundation of China
Received date: 2011-07-27; Accepted date: 2011-12-22
Corresponding author: HUANG Jun-xin, PhD; Tel: +86-734-6666858; E-mail: amwwcwujqw@126.com
