DOI: 10.11817/j.issn.1672-7207.2015.11.014
考虑能耗优化的双足步行机器人柔性关节研究
张强,肖晓晖,王杨,游鹏辉,谢涛
(武汉大学 动力与机械学院,湖北 武汉,430072)
摘要:为了优化双足步行机器人行走过程中的能量消耗,建立机器人的柔性踝关节和柔性膝关节,分析在机器人单腿支撑阶段,矢状面运动中柔性关节的刚度对关节电机输出转矩和能量消耗的影响。首先,建立双足步行机器人的5连杆模型,分别在该模型的踝关节和膝关节对柔性进行改进;其次,采用基于零力矩点(zero moment point, ZMP)稳定判据的步态规划方法,通过给定ZMP轨迹获取机器人质心轨迹,插值得到机器人在刚性路面的离线步态;最后,基于改进的柔性关节5连杆步行机器人模型,分别采用拉格朗日方程解析法和虚拟样机动力学仿真法,分析柔性踝关节和膝关节的刚度对关节电机输出转矩和能量消耗的影响。研究结果表明:适当选择柔性关节的刚度可以有效地减小关节电机的输出转矩和能量消耗;柔性踝关节和膝关节分别存在1个最佳刚度,在此刚度下关节电机的能量消耗可以降到最小,与解析法中刚性关节相比分别减小89.87%和90.11%,与动力学仿真中刚性关节相比分别减小88.66%和81.23%。
关键词:柔性关节;双足步行机器人;步态规划;拉格朗日方程;能量消耗
中图分类号:TP24;TH113 文献标志码:A 文章编号:1672-7207(2015)11-4070-07
Compliant joint for biped robot considering energy consumption optimization
ZHANG Qiang, XIAO Xiaohui, WANG Yang, YOU Penghui, XIE Tao
(School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China)
Abstract: In order to optimize the energy consumption of biped robot while walking, the compliant joint for biped walking robots was proposed to investigate the influence of ankle joint and knee joint stiffness on motor torque and energy consumption of the sagittal plane motion during the single support phase. Firstly, an improved model of the five-link biped robot was established, which is the theoretical foundation of the compliant joint. Then, with gait planning based on natural zero moment point (ZMP) trajectory, the robot’s center of mass (COM) rack was obtained by setting ZMP trajectory, and the gait on a rigid path was acquired by interpolation. Finally, both the Lagrange equations analytic method and dynamic simulations were performed to analyze the influences of compliant joint stiffness on motor torque and energy consumption based on the improved model of the five-link biped robot. The results show that the compliant joint can reduce the joint motor torque and energy consumption effectively. There is an optimal stiffness of the compliant ankle joint and knee joint respectively, which can minimize the motor energy consumption with a reduction of 89.87% and 90.11% in analytic method, as well as 88.66% and 81.23% in dynamic simulations.
Key words: flexible joint; biped robot; gait planning; Lagrange equations; energy consumption
近年来,双足步行机器人已经成为机器人研究领域的热点。由于步行机器人具有环境适应性好、运动协调能力强以及能量消耗低等优势,在医疗、助老助残和家庭服务等方面具有广阔的应用前景,也是揭示人体运动机理的重要研究平台。双足步行机器人由2条腿和1个平台(腰部)组成。腿的作用是为平台提供移动能力,而平台作用则是提供基础,以便安装机械手、控制系统和蓄电池等[1]。研究表明步行机器人支撑腿比摆动腿消耗能量更多,原因是支撑腿实现整个机器人在地面站立需要很大的关节转矩。因此,改善步行机器人支撑腿关节能量消耗效率对于优化机器人行走是十分必要的。然而,目前对于双足步行机器人的研究大多采用多刚体机器人作为研究对象,同时在双足步行运动过程中,机器人足部和地面环境之间存在很多碰撞,这些碰撞对于机器人实现稳定步行是非常不利的,因此,引入柔性关节在减小碰撞和降低能耗方面显得尤为重要。双足步行从生物力学角度可以分为基于主动控制的运动和基于被动行走的运动。近年来,具有柔性关节或驱动的机器人跟踪控制吸引了很多研究者的关注。黄岩等[2]认为主动被动结合的双足步行机器人具有效率高、步态自然、实用性强等特点,最主要的方法就是在双足步行机器人中加入可控的柔性。Migliore等[3]基于人类肌肉驱动的原理设计了1种对抗控制柔性的驱动器,该驱动器由2个电机和2个弹簧组成,可以实现对关节柔性的控制。Vanderborght等[4]用气动人工肌肉作为驱动器,研制了双足机器人Lucy,在该机器人中有轨迹发生器和关节轨迹跟踪器,其控制思想是根据期望的关节轨迹来调整驱动器的柔性,使机器人肢体的固有频率与期望轨迹的频率尽可能接近,以达到提高运动效率的目的。Owaki等[5]在被动动态双足运动仿真模型中加入类似人的髋关节柔性和腿部柔性,研究了包括奔跑、跳跃、行走在内的多种步态在不同柔性下的分布。Huang等[6]研究了具有平脚结构和踝关节柔性的动态双足行走模型的步态选择,结果表明踝关节柔性在产生不同的行走步态中发挥很大的作用,并揭示了与人类自然行走最接近的步态具有最高的运动效率。同时,一些研究机构也进行了在实体双足机器人上加入可控柔性的工作[7-9]。Haq等[10]研究了在全驱动七连杆步行机器人不同关节上附加扭簧和膝关节锁定对于能量消耗的作用,其研究重点是机器人步行过程中能耗如何降低。Tsagarakis等[11]提出了最近研发的柔性仿人机器人(COMAN),设计了基于一系列弹性驱动原则的被动柔性驱动器,该步行机器人完成步行运动正是被这种驱动器所驱动。由上述研究可知基于被动行走的双足机器人由于其运动方式与人类更接近,且对驱动器的要求相对较低,所以,目前大多数研究工作集中在被动双足步行机器人的柔性驱动;而基于主动控制的双足步行机器人大多还是以实现精确的位置控制为目标,柔性关节或驱动对机器人动力学参数影响等方面的研究较少。为此,本文作者在已有研究的基础上,考虑一种改进的柔性踝关节和膝关节,通过多组仿真分析揭示单腿支撑相(SSP)踝关节和膝关节的柔性对关节电机转矩和能量消耗的影响。
1 柔性关节数学模型
人腿在适应环境中不断改进,最终进化为大部分由柔性组织构成的结构,尤其是关节连接处,虽然是骨骼系统,但也是通过软骨和韧带相互连接和固定的,因此,人腿关节表现出很强的黏弹性。为了提高步行机器人的环境适应能力和运动效率,在双足步行机器人的关节处引入柔性很有必要,这意味着在关节旋转过程中存在黏弹性。以支撑腿为对象,展示本研究所建立的改进的带有柔性踝关节和膝关节的5连杆步行机器人模型,见图1[12]。图1中: 为踝关节转角;
为踝关节转角;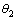 为膝关节转角;
为膝关节转角; 和
和 为小腿连杆质量;
为小腿连杆质量;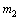 和
和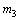 为大腿连杆质量;
为大腿连杆质量; 为机器人上身质量;
为机器人上身质量; 和
和 为小腿连杆长度;
为小腿连杆长度; 和
和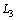 为大腿连杆长度;
为大腿连杆长度; 和
和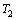 分别为踝关节和膝关节的电机输出转矩;
分别为踝关节和膝关节的电机输出转矩;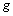 为重力加速度;同时规定逆时针旋转为关节轨迹正方向。该模型揭示了所研究柔性关节的原理,采用弹簧阻尼系统实现关节的柔性化。其中,柔性踝关节包括踏板、弹簧和安装板,其中踏板是踝关节的基础,踏板与机器人的足底固定在一起;柔性膝关节包括大腿连杆安装板、弹簧和小腿连杆安装板。关节的刚度取决于弹簧的刚度,因此,弹簧刚度的选择对机器人实现稳定行走尤其重要。若刚度选择太小,则弹簧发生小变形,抵消关节电机输出转矩的能力较小,需要关节电机的输出转矩较大,电机能耗不会明显减小;若弹簧刚度选择太大,则相同形变下产生的弹力很大,达到规划的轨迹需要电机增大输出转矩,使弹簧发生形变,此时会起相反的效果,电机能耗反而会增大。本文针对柔性关节的基本研究思路是机器人重力的优化利用。该关节可以在矢状面吸收用于向前和向后摆动腰部的能量,在单腿支撑相,若弹簧刚度选择合适,则踝关节和膝关节电机可以输出很小转矩,机器人腰部前向运动由重力作用自然完成。基于改进的5连杆步行机器人模型,柔性关节的拉格朗日第2类方程可以表示为
为重力加速度;同时规定逆时针旋转为关节轨迹正方向。该模型揭示了所研究柔性关节的原理,采用弹簧阻尼系统实现关节的柔性化。其中,柔性踝关节包括踏板、弹簧和安装板,其中踏板是踝关节的基础,踏板与机器人的足底固定在一起;柔性膝关节包括大腿连杆安装板、弹簧和小腿连杆安装板。关节的刚度取决于弹簧的刚度,因此,弹簧刚度的选择对机器人实现稳定行走尤其重要。若刚度选择太小,则弹簧发生小变形,抵消关节电机输出转矩的能力较小,需要关节电机的输出转矩较大,电机能耗不会明显减小;若弹簧刚度选择太大,则相同形变下产生的弹力很大,达到规划的轨迹需要电机增大输出转矩,使弹簧发生形变,此时会起相反的效果,电机能耗反而会增大。本文针对柔性关节的基本研究思路是机器人重力的优化利用。该关节可以在矢状面吸收用于向前和向后摆动腰部的能量,在单腿支撑相,若弹簧刚度选择合适,则踝关节和膝关节电机可以输出很小转矩,机器人腰部前向运动由重力作用自然完成。基于改进的5连杆步行机器人模型,柔性关节的拉格朗日第2类方程可以表示为
 (1)
(1)
式中: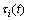 为踝关节和膝关节电机的转矩;
为踝关节和膝关节电机的转矩;
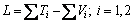 (2)
(2)
 (3)
(3)
 (4)
(4)
其中: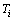 和
和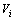 分别为各杆的动能和势能;
分别为各杆的动能和势能; 和
和 为各杆在X和Y方向上的质心位移;
为各杆在X和Y方向上的质心位移; 为各杆转动惯量;
为各杆转动惯量; 为踝关节和膝关节弹簧的劲度系数;
为踝关节和膝关节弹簧的劲度系数;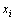 为踝关节和膝关节弹簧的弹性形变。
为踝关节和膝关节弹簧的弹性形变。
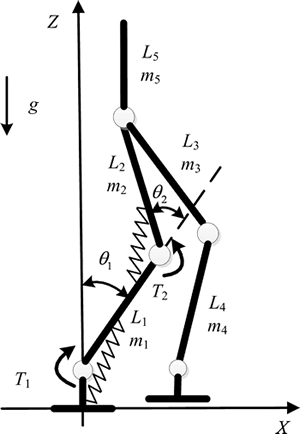
图1 关节柔性化的5连杆步行机器人模型
Fig. 1 Improved five-link biped robot model with compliant joint
机器人初始状态为直立,踝关节和膝关节弹簧均没有发生形变。机器人在行走过程中,弹簧两端的定位安装点与对应的关节旋转中心组成1个三角形,据余弦定理,式(4)中弹簧的形变量可以表示为
 (5)
(5)
根据式(1)和(2),关节电机能耗可以表示为
 (6)
(6)
要证明引入该种柔性踝关节和膝关节的优势比较复杂。本文通过拉格朗日第2类方程的理论计算分析踝关节和膝关节关节刚度与关节电机动态参数之间的关系。
2 基于ZMP判据的离线步态规划
2.1 步态规划流程
ZMP作为动态步行稳定性的判定标准[13-15]对于理解动态稳定性及检测和控制行走机器人很重要[13-15]。ZMP处重力和惯性力产生的作用在机器人上的倾覆力矩为0 N·m [16]。基于车子-小车模型[17],可将ZMP的坐标表达为:
 (7)
(7)
 (8)
(8)
其中: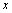 和
和 分别为质心的X向和Y向位移;
分别为质心的X向和Y向位移; 和
和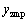 分别为ZMP点在X向和Y向位移。
分别为ZMP点在X向和Y向位移。
基于ZMP判据的步态规划,其流程包括:规划机器人的足部轨迹与ZMP轨迹;通过ZMP方程式求解质心轨迹;根据正运动学求解相关部分的运动轨迹;根据逆运动学求解机器人的各关节角轨迹和确定机器人的空间位姿等。
2.2 足部轨迹规划
根据人类行走过程,1个完整的步行周期由单腿支撑相(SSP)和双腿支撑相(DSP)这2个阶段组成。步行机器人通过交替的双足踏地来实现移动,所以,在足接触地面的瞬间,足底与地面之间产生冲击力,并且足部落地速度越大,冲击力越大,关节电机转矩峰值越大。为了减小冲击力,规划足部在矢状面内的运动轨迹为正弦曲线,这样,机器人足部在最高处水平速度最大,在离地和落地瞬间竖直方向速度最小,可以有效减少冲击。双足步行机器人足部在矢状面内的运动轨迹如图2所示。
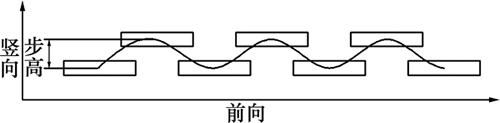
图2 机器人足部运动轨迹
Fig. 2 Vertical trajectory of biped robot’s feet
2.3 ZMP轨迹规划
本文将机器人运动的前向、侧向和竖向分别规定为X轴、Y轴和Z轴。为了方便步态规划和分析,进行如下假设:1) 步行机器人在行走过程中前进的方向为X轴正方向;2) 行走过程中左右足关于X轴对称;3) 行走过程中机器人的质心在Z方向的高度保持一致;4) 在迈步过程中,足底与地面保持平行。本文采用的参考ZMP轨迹如图3所示。
步行机器人行走是1个单足支撑相和双足支撑相不断交替的过程。当单足支撑相、只有单足固定在地面上时,整个运动系统可被视为1个开环的树状运动链,支撑面积就是接触地面的足部面积;当双足支撑相、双足均固定在地面上时,整个运动系统可被视为1个过驱动的闭环运动链,支撑面为双足和其组成的凸多边形。ZMP轨迹在支撑凸多边形内部是机器人稳定行走的必要条件。
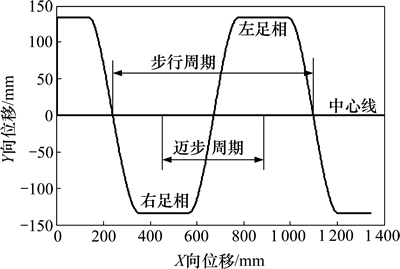
图3 参考ZMP轨迹
Fig. 3 Trajectory of reference ZMP
2.4 质心轨迹求解
ZMP方程(7)和(8)用采样时间 离散化[18]后,加速度
离散化[18]后,加速度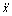 和
和 可近似为
可近似为
 (9)
(9)
 (10)
(10)
离散后的ZMP方程为
 (11)
(11)
 (12)
(12)
其中: ;
; 。
。
将对应于时间段1, 2, …, N的式(11)和(12)合并在一起,zc表示质心高度,写成矩阵形式,则质心轨迹为[19]
 (13)
(13)
 (14)
(14)
式中:
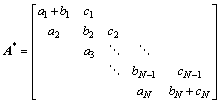
 ,
,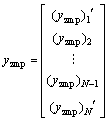
当步行机器人的X向和Y向ZMP轨迹给定时,由式(13)和(14)可以求出质心轨迹如图4所示。
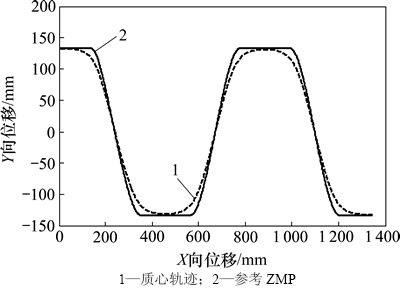
图4 基于参考ZMP的质心轨迹
Fig. 4 Trajectory of COM based on reference ZMP
针对求解得到的质心轨迹,逆运动学反求双足步行机器人各个关节角轨迹。基于建立的关节柔性化的5连杆机器人模型,采用反求的机器人各关节角轨迹,就可以通过解析法和虚拟样机动力学仿真法来研究在单腿支撑相踝关节和膝关节的柔性对关节电机转矩和能耗的影响。
3 柔性关节仿真分析
3.1 解析法柔性关节对转矩的影响
图1所示的5连杆模型参数如下:L1 = L2 = 0.35 m,m1 = m2 = 1.8 kg,m5 = 13 kg,g = 9.8 m/s2,步行周期T=3 s。由于分析左腿支撑相的左腿关节与右腿支撑相的右腿关节采用的方法相同,结果类似,为此,本文以1个步行周期内左腿支撑相左腿踝关节和膝关节为研究对象。根据离线的步态规划可以得到左腿支撑相起始时间点和结束时间点,在这段时间内,其踝关节轨迹和膝关节轨迹变化如图5所示。
步行机器人各个关节电机有效完成所规划的对应轨迹是其能够实现稳定行走的必要条件。电机的输出转矩作为电机的1个重要性能指标,在很大程度上决定了关节能否实现完整的运动。相对于传统的刚性关节,柔性关节的刚度取决于弹簧阻尼系统的劲度系数。根据关节转角的变化,可以进行插值求解转角与时间的函数关系,通过式(1)计算得到踝关节和膝关节在柔性和刚柔性情况下电机输出转矩的变化,如图6所示(规定关节电机转矩正方向为逆时针方向)。图6中,柔性关节刚度为1 kN/m。

图5 踝关节轨迹和膝关节轨迹
Fig. 5 Ankle joint trajectory and knee joint trajectory

图6 踝关节电机转矩和膝关节电机转矩
Fig. 6 Ankle joint motor torque and knee joint motor torque
通过对比分析图6中的曲线,在步行机器人单腿支撑相,柔性关节电机的输出转矩明显小于刚性关节的输出转矩,并且这种减小输出转矩的能力取决于柔性关节的刚度。本文选取从0~20 kN/m间隔为100 N/m的200种不同关节刚度进行仿真分析。如图7所示,以关节刚度为1,3,5,7和9 kN/m为例分析关节刚度对关节电机转矩的影响。图7(a)和图7(b)所示分别为踝关节刚度和膝关节刚度对关节电机输出转矩的影响。从图6(a)和图6(b)可见:当关节为刚性时,踝关节的电机输出转矩为逆时针方向,膝关节的电机输出转矩为顺时针方向,此时电机转矩均起到制动作用;在给出的关节刚度范围之内,随着刚度增大,关节电机输出转矩减小;当关节刚度继续增大时,电机的输出转矩会反向增大,此时电机转矩起到驱动作用;若刚度过大,则电机的额定转矩不能够提供足够的驱动来完成关节的运动轨迹,导致步行机器人无法正常稳定行走。
3.2 解析法柔性关节对能耗的影响
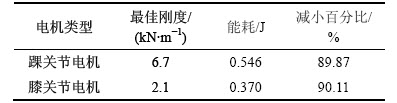
采用上面所选取的200种不同关节刚度,在每种刚度下关节电机输出转矩对转角(轨迹)积分可以得到在单腿支撑相关节电机的能耗。将每种刚度下的电机能耗与刚性关节电机能耗进行对比,寻求最节能的柔性关节刚度。解析法中刚性踝关节和膝关节的电机能耗分别为5.386 J和3.738 J。根据式(6),通过改变柔性关节的刚度,可以计算出每种柔性关节刚度所对应的电机能耗,电机能耗与关节刚度的关系如图8所示。从图8可以得出柔性踝关节和柔性膝关节电机能耗基本上随着关节刚度增大而增大的变化趋势。在仿真所选取的关节刚度范围内,2个关节均存在1个最佳的关节刚度能够使关节电机能耗达到最小值。以这个最佳刚度为分界点,关节刚度从0增大到最佳刚度,电机能耗逐渐减小;关节刚度大于最佳刚度并继续增大,电机能耗会逐渐增大。与刚性关节相比,解析法中柔性关节的最佳刚度、最佳刚度下的电机能耗以及电机能耗减小百分比如表1所示。
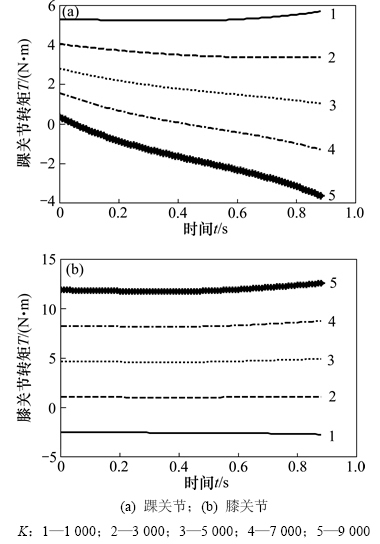
图7 不同关节刚度的电机转矩
Fig. 7 Joint motor torque of different joint stiffness
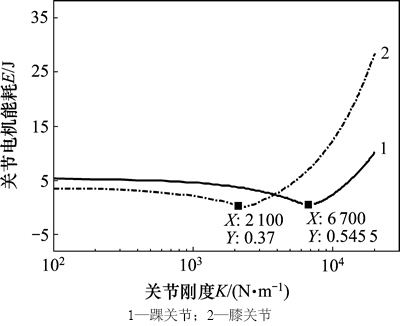
图8 解析法中不同关节刚度的电机能耗
Fig. 8 Joint motor energy consumption of different joint stiffnesses in analytic method
表1 解析法中最佳刚度柔性关节的电机能耗
Table 1 Motor energy consumption of compliant joint with optimal stiffness in analytic method
3.3 动力学仿真法柔性关节对能耗的影响
为了进一步探索基于改进5连杆模型建立的柔性关节对关节动力学参数的影响,同时验证解析法中柔性关节在能耗优化方面所达到的效果,在动力学仿真软件ADAMS中建立步行机器人虚拟样机进行仿真分析。该动力学仿真是以机器人各关节空间协调运动为基础,离线步态规划计算各关节运动的离散值,利用ADAMS的三次样条插值函数将这些离散值拟合成连续曲线,产生角度-时间的连续函数,作为各个关节的驱动。
在仿真中不考虑所加入的弹簧阻尼系统的质量,弹簧装置不会改变机器人的参数,并且其消耗的能量可以忽略不计;同时不考虑关节运动摩擦,即没有能量损失。基于以上2条假设,通过改变关节弹簧劲度系数K来改变柔性关节的刚度。选取10种柔性关节刚度进行10组仿真,得出在单腿支撑相阶段每种柔性关节刚度所对应的电机能耗,电机能耗与关节刚度的关系如图9所示。从图9可以看出:随着柔性关节刚度增大,动力学仿真中关节电机能耗的变化趋势与解析法中得到的趋势相同。
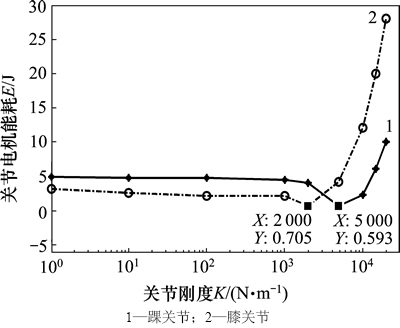
图9 动力学仿真中不同关节刚度的电机能耗
Fig. 9 Joint motor energy consumption of different joint stiffnesses in dynamic simulation
动力学仿真中刚性踝关节和膝关节的电机能耗分别为5.231 J和3.755 J。动力学仿真中柔性关节的最佳刚度、最佳刚度下的电机能耗以及电机能耗减小百分比如表2所示。
拉格朗日解析法与虚拟样机动力学仿真法所得到的结果存在一定的差异,在给定相同模型参数下,这2种方法对应关节的最佳刚度和能耗减小百分比均存在差异。其原因是:1) 解析法中5连杆虽然有质量和长度,但仍然是理想的均质杆,在虚拟样机动力学仿真中每个零件都有自己的尺寸和质量,在运动过程中会有各个方向的惯量产生;2) 在动力学仿真过程中,步态会发生变化并且足部与地面之间会产生碰撞。
表2 动力学仿真中最佳刚度柔性关节的电机能耗
Table 2 Motor energy consumption of compliant joint with optimal stiffness in dynamic simulation

4 结论
1) 基于5连杆双足步行机器人模型,在矢状面对机器人的踝关节和膝关节进行柔性化改进,以减小关节电机在单腿支撑相的输出转矩和能量消耗,通过解析法和动力学仿真方法证明柔性关节的有效性。
2) 随着柔性关节的刚度从0 N·m逐渐增大,在单腿支撑相,支撑腿踝关节和膝关节电机的输出转矩首先会减小,减小到0 N·m之后会反向增大,此时转矩的效果会由制动变为驱动;同时,踝关节和膝关节电机能耗也会先减小后增大,2个关节均存在1个最佳关节刚度使关节电机能耗达到最小值。与关节刚度为0 N·m的电机能耗相比,在解析法中最佳刚度踝关节和膝关节电机能耗分别降低89.87%和90.11%;在动力学仿真中最佳刚度踝关节和膝关节电机能耗分别降低88.66%和81.23%。
3) 所建立的柔性关节只考虑了步行机器人矢状面运动,而没有考虑其侧向平面运动。
下一阶段的研究如下:为了验证理论结果的正确性,物理样机实验是必不可少的,为此,需搭建基于主动控制柔性关节步行机器人的实验平台;设计一种综合矢状面和侧向平面运动的柔性关节,讨论2个平面运动之间的耦合作用。
参考文献:
[1] Silva M F, Machado J A T. A historical perspective of legged robots[J]. Journal of Vibration and Control, 2007, 13(9/10): 1447-1486.
[2] 黄岩, 王启宁, 谢广明. 具有可控柔性的双足行走机器人研究进展综述[J]. 兵工自动化, 2012, 31(12): 45-52.
HUANG Yan, WANG Qining, XIE Guangming. Review of bipedal walking robots with adaptable compliance[J]. Ordnance Industry Automation, 2012, 31(12): 45-52.
[3] Migliore S, Brown E, DeWeerth S P. Biologically inspired joint stiffness control[C]// IEEE International Conference on Robotics and Automation. Barcelona, Spain, 2005: 4508-4513.
[4] Vanderborght B, Verrelst B, van Ham R, et al. Development of a compliance controller to reduce energy consumption for bipedal robots[J]. Autonomous Robots, 2008, 24(4): 419-434.
[5] Owaki D, Osuka K, Ishiguro A. On the embodiment that enables passive dynamic bipedal running[C]// IEEE International Conference on Robotics and Automation. Pasadena, USA, 2008: 341-346.
[6] HUANG Yan, WANG Qining, CHEN Baojun, et al. Modeling and gait selection of passivity-based seven-link bipeds with dynamic series of walking phases[J]. Robotica, 2012, 30(1): 39-51.
[7] van Ham R, Vanderborght B, van Damme M, et al. MACCEPA, the mechanically adjustable compliance and controllable equilibrium position actuator: design and implementation in a biped robot[J]. Robotics and Autonomous Systems, 2007, 55(10): 761-768.
[8] Hosoda K, Takuma T, Nakamoto A, et al. Biped robot design powered by antagonistic pneumatic actuators for multi-modal locomotion[J]. Robotics and Autonomous Systems, 2008, 56(1): 46-53.
[9] Rummel J, Blum Y, Maus H M, et al. Stable and robust walking with compliant legs[C]// IEEE International Conference on Robotics and Automation. Anchorage, USA, 2010: 5250-5255.
[10] Haq A, Aoustin Y, Chevallereau C. Effects of knee locking and passive joint stiffness on energy consumption of a seven-link planar biped[C]// IEEE International Conference onRobotics and Automation. Saint Paul, USA, 2012: 870-876.
[11] Tsagarakis N G, Morfey S, Cerda G M, et al. Compliant humanoid coman: Optimal joint stiffness tuning for modal frequency control[C]// IEEE International Conference on Robotics and Automation. Karlsruhe, Germany, 2013: 673-678.
[12] 槐创锋, 方跃法. 5连杆双足机器人建模和控制系统仿真[J]. 系统仿真学报, 2008, 20(20): 5682-5686.
HUAI Chuangfeng, FANG Yuefa. Modeling and control system simulation for 5-link biped robot[J]. Journal of System Simulation, 2008, 20(20): 5682-5686.
[13] Vukobratovic M, Borovac B, Potkonjak V. Towards a unified understanding of basic notions and terms in humanoid robotics[J]. Robotica, 2007, 25(1): 87-101.
[14] Vukobratovic M, Frank A A, Jricic D. On the stability of biped locomotion[J]. IEEE Transactions on Biomedical Engineering, 1970, 1(BEM-17): 25-36.
[15] Vukobratovic M, Brovac B. Zero-moment point-thirty five years of its life[J]. Journal of Humanoid Robotics, 2004, 1(1): 157-173.
[16] Czarnetzki S, Kerner S, Urbann O. Observer-based dynamic walking control for biped robots[J]. Robotics and Autonomous Systems, 2009, 57(8): 839-845.
[17] Kuffner J, Nishiwaki K, Kagami S. Motion planning for humanoid robots under obstacle and dynamic balance constraints[C]// IEEE International Conference on Robotics and Automation. Seoul, Korea, 2001: 692-698.
[18] Ugurlu B, Kawamura A. ZMP-based online jumping pattern generation for a one-legged robot[J]. IEEE Transactions on Industrial Electronics, 2010, 57(5): 1701-1709.
[19] 韩亚丽, 王兴松, 罗翔. 双足机器人稳定行走步行模式的研究[J]. 东南大学学报(自然科学版), 2009, 39(2): 238-244.
HAN Yali, WANG Xingsong, LUO Xiang. Study of stabilization walking pattern for biped robot[J]. Journal of Southeast University (Natural Science Edition), 2009, 39(2): 238-244.
(编辑 陈灿华)
收稿日期:2015-04-01;修回日期:2015-06-08
基金项目(Foundation item):国家自然科学基金资助项目(51175383) (Project(51175383) supported by the National Natural Science Foundation of China)
通信作者:肖晓晖,博士,教授,博士生导师,从事特种机器人技术与机器人动力学科研与教学工作;E-mail: xhxiao@whu.edu.cn