J. Cent. South Univ. (2012) 19: 2488-2495
DOI: 10.1007/s11771-012-1301-1
Robust stabilization and disturbance attenuation for a class of underactuated mechanical systems
LAI Xu-zhi(赖旭芝)1,2, PAN Chang-zhong(潘昌忠)1,2,4, WU Min(吴敏)1,2, SHE Jin-hua(佘锦华)3, Simon X. YANG 4
1. School of Information Science and Engineering, Central South University, Changsha 410083, China;
2. Hunan Engineering Laboratory for Advanced Control and Intelligent Automation (Central South University), Changsha 410083, China;
3. School of Computer Science, Tokyo University of Technology, Tokyo 192-0982, Japan;
4. School of Engineering, University of Guelph, Guelph N1G 2W1, Canada
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: The robust control problem for a class of underactuated mechanical systems called acrobots is addressed. The goal is to drive the acrobots away from the straight-down position and balance them at the straight-up unstable equilibrium position in the presence of parametric uncertainties and external disturbance. First, in the swing-up area, it is shown that the time derivative of energy is independent of the parameter uncertainties, but exogenous disturbance may destroy the characteristic of increase in mechanical energy. So, a swing-up controller with compensator is designed to suppress the influence of the disturbance. Then, in the attractive area, the control problem is formulated into a H∞ control framework by introducing a proper error signal, and a sufficient condition of the existence of H∞ state feedback control law based on linear matrix inequality (LMI) is proposed to guarantee the quadratic stability of the control system. Finally, the simulation results show that the proposed control approach can simultaneously handle a maximum ±10% parameter perturbation and a big disturbance simultaneously.
Key words: underactuated mechanical systems; robust stabilization; disturbance attenuation; H∞; linear matrix inequality (LMI)
1 Introduction
The control of underactuated mechanical systems, which have less control inputs than generalized coordinates, has received increasing attention [1-5]. Since mechanical systems have a potential for downsizing, lightening, energy-saving and cost-down, they have been received a great deal of attention from both the academic and the industrial fields over the last few decades. An underactuated two-link manipulator moving in a vertical plane, which possesses an actuated joint at the elbow and a passive joint at the shoulder, is called an acrobot [6]. This kind of manipulators has been used as a test-bed for proposed control methods. Therefore, the investigation of underactuated two-link manipulators is of great importance both in control theory and applications.
Generally speaking, in order to simplify the design problem of the control system, it is very common to divide the motion space of this class of underactuated system into two subspaces: the swing-up area and the attractive area [5]. Many control strategies have been devised for each area. For example, partial feedback linearization [6-7], rewinding approach [8], energy-based method [9-10], and impulse-momentum approach [11], have been proposed for the swing-up control; LQR [5-6], sliding mode control [12], and quotient method [13], have been employed for the balancing control. However, most control methods in the previous works only considered a nominal model. It is known that there may be some uncertainties in the parameters, and the system may suffer from exogenous disturbances. In order to derive a practical control method, it is important to investigate the robust stabilization issue under the existence of parameter uncertainties as well as external disturbances.
To solve this problem, BERGERMAN and XU [14] proposed a variable structure control method to handle the modeling errors, and QIAN et al [15] considered the mismatched uncertainties using hierarchical sliding mode control. In Ref. [16], O’FLAHERTY et al validated a hybrid control algorithm for a pendubot, and examined its robustness to exogenous disturbances through experiments. But theoretical analysis was not given. XIN and KANEDA [17] proposed a robust control method for the swing-up of an acrobot by treating the speed of the second link in the attractive area as an uncertainty. YAZICI and KARAMANCIOGLU [18] tested the robust stability of a control system under a fixed linear quadratic controller at the upright position by using a real-structured singular value model. However, these methods only considered the robust stability problem in the attractive area. In addition, ORLOV et al [19] employed H∞ theorem to the swing-up control of a pendubot, but parameter uncertainties were not considered. At present, the robust control problem under both parameter uncertainties and disturbances in the whole motion space has been left unsolved.
On the other hand, H∞ control theory has made a remarkable progress over the last few decades. The advantage of using the framework of H∞ control is that we can handle the robust stabilization of an uncertain system, disturbance attenuation, etc, in a standard problem setting, and can easily solve them using the linear matrix inequality (LMI) technique [20]. Many attempts have been made on applying H∞ control to robotic systems [21-23]. However, few can be found on underactuated mechanical systems.
In this work, the robust stabilization and disturbance attenuation problem of an underactuated two-link manipulator such as acrobot, in which parameter uncertainties and an exogenous disturbance exist, is addressed. In particular, a torque disturbance caused by the AC power supply of the motor mounted at the actuated joint is considered. In the swing-up area, a swing-up control law is designed to guarantee that the system energy is non-decreasing with each swing in the presence of the parameter uncertainties and the disturbance. Then, in the attractive area, a robust control law is designed to guarantee the quadratic stability of the control system. It employs an uncertain linear model of the manipulators at the straight-up unstable equilibrium position. We investigate how to transform the design problem to a standard H∞ control, and gain the robust control law by LMI technique. Simulations on an acrobot with large uncertainties are presented to show the good robustness of the control system.
2 Dynamics and problem statement
The dynamic model of an underactuated two-link manipulator with uncertainties is presented, and then the division of the motion space is described.
2.1 Dynamics of acrobot with uncertainties
Figure 1 shows the model of an acrobot. For j=1, 2, qj is the angle of the j-th link measured relative to the vertical for the link attached to the base or relative to the front link; mj and Lj are the mass and length of the j-th link, respectively; Lgj is the distance from the j-th joint to the center of mass of the j-th link; Ij is the moment of inertia of the j-th link about its centroid.
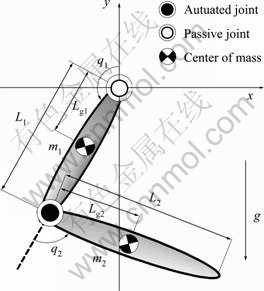
Fig. 1 Model of an acrobat
The dynamics of underactuated mechanical systems with uncertainties are given by
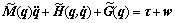 (1)
(1)
where 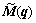 is the inertia matrix;
is the inertia matrix; 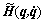 is the combination of the Coriolis and centrifugal forces;
is the combination of the Coriolis and centrifugal forces; 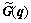 is the force of gravity;
is the force of gravity; 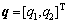 , and
, and 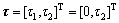 . Note that
. Note that 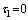 indicates that Joint 1 is passive.
indicates that Joint 1 is passive. 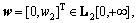 is an arbitrary disturbance. In particular, we consider w to be a signal with sine or cosine components that represent disturbances in real mechatronic systems, e.g., a disturbance caused by the AC power supply of a motor driver. Letting d be a known non-negative real number, we have
is an arbitrary disturbance. In particular, we consider w to be a signal with sine or cosine components that represent disturbances in real mechatronic systems, e.g., a disturbance caused by the AC power supply of a motor driver. Letting d be a known non-negative real number, we have
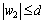 (2)
(2)
In this work, we decompose the terms to be
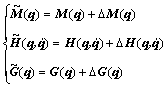 (3)
(3)
where 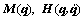 and
and 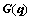 are the nominal parts;
are the nominal parts; 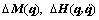 and
and  are the uncertainties. They are expressed by
are the uncertainties. They are expressed by
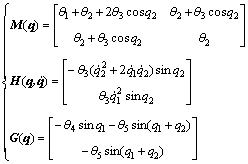 (4)
(4)
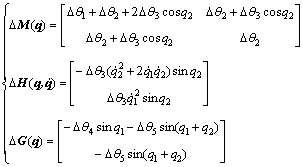 (5)
(5)
where 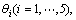 are the structural parameters of the system. They are as follows:
are the structural parameters of the system. They are as follows:
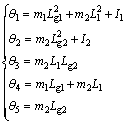 (6)
(6)
where 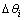 (i=1, 2, …, 5) are the parameter uncertainties caused by m1, m2, L1, L2, Lg1, Lg2, I1 and I2.
(i=1, 2, …, 5) are the parameter uncertainties caused by m1, m2, L1, L2, Lg1, Lg2, I1 and I2.
Assuming 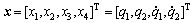 and letting
and letting 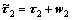 , rewriting the dynamics Eq. (1) in the state space yields the following nonlinear model:
, rewriting the dynamics Eq. (1) in the state space yields the following nonlinear model:
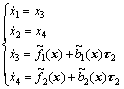 (7)
(7)
where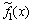 ,
, 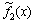 ,
, 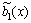 and
and 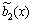 are nonlinear functions given by
are nonlinear functions given by
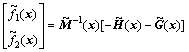 (8)
(8)
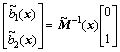 (9)
(9)
Therefore, the control of an underactuated manipulator to be solved in this work can be stated as follows: For system Eq. (7), design a swing-up controller and a balancing controller such that,
1) The system is quadratically stable under any bounded perturbations 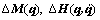 and
and 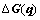 ;
;
2) The closed-loop system has a prescribed disturbance attenuation level for any exogenous disturbance 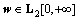 .
.
2.2 Divison of motion division and switching strategy
An underactuated two-link manipulator is a complex nonlinear system. It is known that an adequate division of the motion space can greatly increase the motion control efficiency. We define the motion space as follows.
Definition 1: Let the whole motion space be 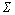 and two state conditions be C1 and C2 as follows
and two state conditions be C1 and C2 as follows
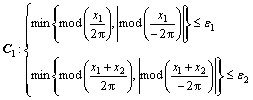 (10)
(10)
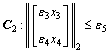 (11)
(11)
where mod(a/b) is the remainder of a divided by b, and its sign is determined by b; 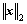 is the two-norm of the vector x;
is the two-norm of the vector x; 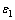 and
and 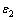 are positive real numbers;
are positive real numbers; 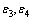 and
and 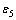 are non-negative real numbers. Then,
are non-negative real numbers. Then,
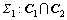 (12)
(12)
 (13)
(13)
are said to be the attractive area and the swing-up area, respectively.
Generally speaking, it allows us to carry out effective motion control by designing different control laws in different subspaces to exactly suit the control objective in each subspace. However, there exists a chattering problem in switching control laws between subspaces. To avoid a big variation in the applied toque when the control law changes from the one for swing-up to the one for balancing, we introduce the following control strategy.
Let E(x) and E0 be the total mechanical energy and the potential energy of the nominal system at the straight-up position, respectively. We consider
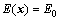 (14)
(14)
when the system satisfies Eq. (14) in 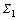 for the first time, we switch the swing-up control law to
for the first time, we switch the swing-up control law to
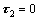 (15)
(15)
where makes the system rotate only under the disturbance w2. Considering the fact that, for a well-designed system, the disturbance w2 is not very big and the system possesses enough mechanical energy. We know that, for most cases, the system will continue moving and enter into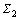 . As a result, there are at least two times of switching of control laws needed in the whole motion space. The first switching takes place when Eq. (14) is satisfied, and the second switching is performed when the system satisfies Eqs. (10) and (11). Note that, between the first and second switching, the applied toque is zero. So, the mechanical energy is almost maintained at E0, and the states change along the movement. This makes the system enter into the attractive area. A brief analysis for the use of E0 is given as follows.
. As a result, there are at least two times of switching of control laws needed in the whole motion space. The first switching takes place when Eq. (14) is satisfied, and the second switching is performed when the system satisfies Eqs. (10) and (11). Note that, between the first and second switching, the applied toque is zero. So, the mechanical energy is almost maintained at E0, and the states change along the movement. This makes the system enter into the attractive area. A brief analysis for the use of E0 is given as follows.
For system Eq. (7), we define
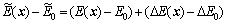 (16)
(16)
where 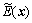 and
and 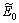 are the total mechanical energy and the potential energy at the straight-up position of the uncertain system.
are the total mechanical energy and the potential energy at the straight-up position of the uncertain system.
Note that
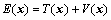 (17)
(17)
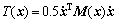 (18)
(18)
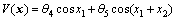 (19)
(19)
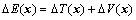 (20)
(20)
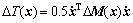 (21)
(21)
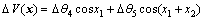 (22)
(22)
where T(x) and V(x) are the kinetic and potential energies of the nominal system, respectively, and ?T(x) and ?V(x) are their uncertain parts.
From Eqs. (17)-(22), it is clear that the mechanical energy of the uncertain system changes in the same trend as that of the nominal system. Since the underactuated manipulators considered here are rigid body systems, we consider the case in which the parameter uncertainties are time invariant. So, when the mechanical energy E(x) converges to E0 gradually under a swing-up controller, ?E(x) has the same trend, and converges to ?E0. When Eq. (14) holds, ?E(x) is equal to ?E0. Therefore, we only need to calculate E(x) using the nominal parameters, and consider the condition (Eq. (14)) for the nominal system to judge whether the system has stored enough energy or not.
3 Design of swing-up controller
Energy based control method [9-10] is an effective strategy for the swing-up motion. However, most of the results did not consider the influence of parameter uncertainties or a disturbance. To design an effective swing-up controller with the existence of parameter uncertainties and the disturbance, we first analyze the influence of those factors on the mechanical energy of the system.
3.1 Relationship between energy and torque
Calculating the time derivative of 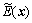 yields
yields
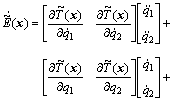
 (23)
(23)
It is easy to show that
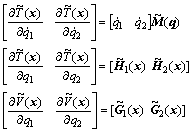 (24)
(24)
and
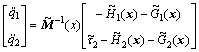 (25)
(25)
Substituting Eqs. (24) and (25) into Eq. (23) yields
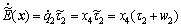 (26)
(26)
Note that the parameter uncertainties do not appear in Eq. (26), and the disturbance is contained in 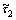 . It is known that the change of the mechanical energy of the system with time is independent of the parameter uncertainties, but is strongly affected by the disturbance.
. It is known that the change of the mechanical energy of the system with time is independent of the parameter uncertainties, but is strongly affected by the disturbance.
3.2 Design of swing-up controller
A swing-up controller is employed to drive the manipulator away from the straight-down stable equilibrium point and towards the straight-up unstable equilibrium point. A physically understandable method is to increase the mechanical energy of the system gradually up to the amount of the potential energy that the system possesses at the straight-up point. Equation (26) shows that the derivative of the mechanical energy with time is only related to two items: x4 and 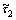 . And as explained in Subsection 2.2, we can observe the mechanical energy of the system by judging from that of the nominal system. So, a swing-up controller ensures the monotonic increase of the mechanical energy if the applied torque
. And as explained in Subsection 2.2, we can observe the mechanical energy of the system by judging from that of the nominal system. So, a swing-up controller ensures the monotonic increase of the mechanical energy if the applied torque 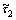 is suitably selected.
is suitably selected.
A swing-up controller based on the following result is designed.
Theorem 1: For Eq. (7), the swing-up control laws
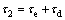 (27)
(27)
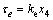 (28)
(28)
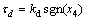 (29)
(29)
guarantee that the system is swung up and the mechanical energy is non-decreasing with each swing. In the control law, ke and kd are suitably selected positive constants, and kd is chosen to satisfy 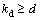 ,
, 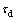 is used to suppress the disturbance, the sgn(·) function in (29) is defined to be
is used to suppress the disturbance, the sgn(·) function in (29) is defined to be
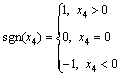 (30)
(30)
Proof: Substituting Eqs. (27)-(30) into Eq. (26) yields
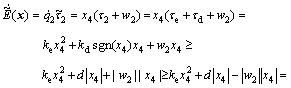
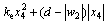 (31)
(31)
From assumption Eq. (2), we know
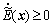 (32)
(32)
Therefore, if we choose the swing-up control law to be Eq. (29), then the mechanical energy of the system will be non-decreasing during the control process.
4 Design of balancing controller
After the system is driven into the attractive area by the swing-up control law (Eq. (27)), a balancing controller is switched to stabilize it at the straight-up position. The existing design methods of a balancing controller are mainly based on the linear approximate model of the normal system (e.g., Refs. [5-6, 12]), and they do not consider the robustness of the control system.
In this work, we present a design method of a balancing controller, which guarantees the quadratic robust stability and a prescribed disturbance attenuation level.
A linear uncertain model in the attractive area is
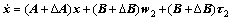 (33)
(33)
where A and B are the known matrices given by the nominal physical parameters of the system, and ?A and ?B are real matrices representing the parameter uncertainties. We consider the disturbance
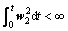 (34)
(34)
and the following uncertainties
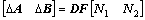 (35)
(35)
where D, N1 and N2 are constant matrices, and F is an unknown matrix with measurable elements satisfying
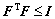 (36)
(36)
Now, for Eq. (33), we design the feedback control
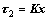 (37)
(37)
to guarantee:
1) The closed-loop system is quadratically stable for all F satisfying Eq. (36);
2) The closed-loop system has the following disturbance attenuation performance:
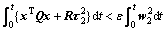 (38)
(38)
for all w2 satisfying Eq. (34). In Eq. (38), 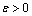 is a constant that describes the disturbance attenuation level;
is a constant that describes the disturbance attenuation level; 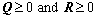 are weights for the state and input, respectively.
are weights for the state and input, respectively.
Note that Eq. (38) is equivalent to
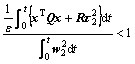 (39)
(39)
Define the error signal to be
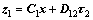 (40)
(40)
where
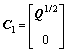 ,
,  (41)
(41)
Note that the new defined error signal z1 is dependent of Q and R. By choosing proper Q and R according to the disturbance attenuation performance Eq. (38), we could get the proper error signal for the attractive area. In addition, let the input and output of F be vF and zF, respectively. Then, as shown in Fig. 2, we can write the generalized plant, G(s), for the design of the state feedback control law (Eq. (37)) with its input and output being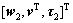 and
and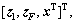 respectively:
respectively:
 (42)
(42)
where
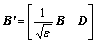 (43)
(43)
Now, the design problem is stated as follows. For the generalized plant G(s), design a state feedback control law that guarantees the internal stability of closed-loop system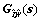 , and satisfies
, and satisfies
 (44)
(44)
where 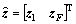 and
and 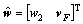 .
.

Fig. 2 Formulation of balancing control in H∞ control
The H∞ design problem can be easily solved using LMI techniques. Applying the algorithm in Ref. [24] to the above design problem yields the following result.
Theorem 2: For the system (Eq. (42)), a sufficient condition of the existence of a state feedback control law Eq. (37) that ensures the robust stability of the closed-loop system satisfies Eq. (44) is that there exists a positive symmetric matrix X and an arbitrary matrix W such that
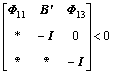 (45)
(45)
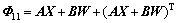
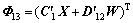
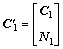 ,
, 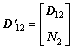
The corresponding H∞ state feedback gain is
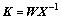 (46)
(46)
5 Simulation results
The nominal parameters of the acrobot are [6]:
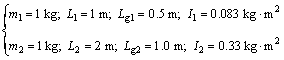
The parameters in Eqs. (10)-(11) are chosen to be
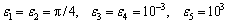
The maximum of the parameter perturbations are assumed to be ±10% of their nominal values, and let
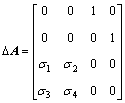 ,
, 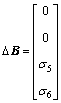
where
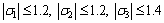 ,
,
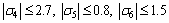
So, D, N1, N2, and F in Eqs. (35)-(36) are
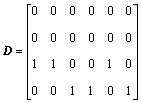 ,
,  ,
,
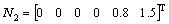 ,
,
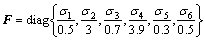
The disturbance caused by the power supply of the motor is supposed to be w2 = 0.5cos(50t). In Eq. (29), kd=0.53, and it is selected a bit bigger than the amplitude of w2 so as to suppress the impact of the disturbance. The parameter of control law in Eq. (28) is selected to be ke=2.1. In Eq. (38), Q=diag{0.25, 0.25, 1, 1}; R=1; 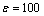 . The initial state is
. The initial state is 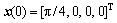 , and E0=24.5 J.
, and E0=24.5 J.
The state feedback control law is obtained by solving Eq. (45) using the Robust Toolbox [25].
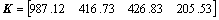 (47)
(47)
Figures 3 and 4 show the simulation results of the acrobot under the disturbance w2=0.5cos(50t) and the presence of parameter changes of +10% and -10%, respectively. The control strategy switches two times. First, at t=0.435 s the mechanical energy increases to E0=24.5 J under the swing-up controller. After that time, the applied torque changes to Eq. (15), and the acrobot rotates without control input. Then, at t=2.410 s, the switching condition for entering the attractive area is satisfied, and the balancing controller takes over. It is noticed from the simulation results that, the system is successfully swung up from the straight-down stable equilibrium point and balanced at the straight-up unstable equilibrium point although it suffers from both parameter changes and external disturbance.
It is worth mentioning that, the large advantage of the presented method is that, unlike the existing methods, e.g., Ref. [16-18], the method presented in this work can handle both parameter uncertainties and an exogenous disturbance in the whole motion space.

Fig. 3 Simulation results with +10% perturbation of parameters and w2 = 0.5cos(50t): (a) q1; (b) q2; (c) τ2; (d) E(x)
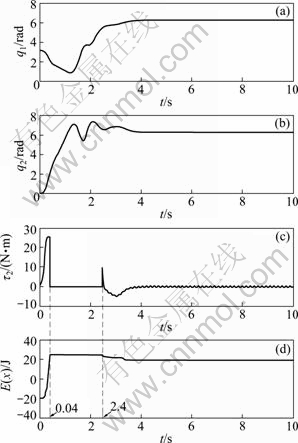
Fig. 4 Simulation results with -10% perturbation of parameters and w2=0.5cos(50t): (a) q1; (b) q2; (c) τ2; (d) E(x)
6 Conclusions
1) A robust control strategy, which can deal with both the parameter uncertainties and disturbances in the whole motion space, is proposed for a class of underactuated mechanical systems. This strategy ensures that the acrobot moves smoothly from the swing-up area into the attractive area, and avoids an abrupt change in the applied torque.
2) A swing-up control law with a compensator is designed to ensure the energy non-decreasing with each swing, and a sufficient condition for the existence of a state feedback control law in the form of LMI is derived to guarantee the quadratic stability of the control system.
3) Simulation results show that the proposed control method can handle a maximum ±10% parameter perturbation and a large disturbance simultaneously. Compared to other methods, the proposed control method has a better robustness to parameters uncertainties and exogenous disturbance.
References
[1] REYHANOGLU M, van der SCHAFT A, MCCLAMROCH N H, KOLMANOVSKY I. Dynamics and control of a class of underactuated mechanical systems [J]. IEEE Transactions on Automatic Control, 1999, 44(9): 1663-1671.
[2] ORTEGA R, SPONG M W, GOMEZ E F, BLANKENSTEIN G. Stabilization of a class of underactuated mechanical systems via interconnection and damping assignment [J]. IEEE Transactions on Automatic Control, 2002, 47(8): 1218-1233.
[3] HUSSEIN I, BLOCH A M. Optimal control of underactuated nonholonomic mechanical systems [J]. IEEE Transactions on Automatic Control, 2008, 53(3): 668-682.
[4] SANKARANARAYANAN V, MAHINDRAKAR A D. Control of a class of underactuated mechanical systems using sliding modes [J]. IEEE Transaction on Robotics, 2009, 25(2): 459-467.
[5] LAI X Z, SHE J H, YANG S X, WU M. Comprehensive unified control strategy for underactuated two-link manipulators [J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B, 2009, 39(2): 389-398.
[6] SPONG M W. The swing up control problem for the acrobot [J]. IEEE Control Systems Magazine, 1995, 15(1): 49-55.
[7] HENMI T, MINGCONG D, INOUE A. Swing-up control of the acrobot using a new partial linearization controller based on the Lyapunov theorem [C]// Proceedings of 2006 IEEE International Conference on Networking, Sensing and Control. Ft. Lauderdale, USA, 2006: 23-25.
[8] SHE J H, LAI X Z, XIN X, GUO L L. A rewinding approach to motion planning for acrobot based on virtual friction [C]// Proceedings of 2010 IEEE International Conference on Industrial Technology (ICIT). Vi a del Mar, 2010: 471-476.
[9] LAI Xu-zhi, WU Min, SHE Jin-hua. Control of acrobat based on Lyapunov function [J]. Journal of Central South University of Technology, 2004, 11(2): 210-215.
[10] FANTONI I, LOZANA R, SPONG M W. Energy based control of the pendubot [J]. IEEE Transactions on Automatic Control, 2000, 45(4): 725-729.
[11] ALBAHKALI T, MUKHERJEE R, DAS T. Swing-up control of the pendubot: an impulse-momentum approach [J]. IEEE Transactions on Robotics, 2009, 25(4): 975-982.
[12] ZHENG Y, YUAN W J. Fuzzy variable structure control for acrobot based on T-S model [C]// IEEE International Conference on Mechatronics and Automation. Niagara Falls, Canada, 2005: 842-846.
[13] WILLSON S S, MULLHAUPT P, BONVIN D. Quotient method for controlling the acrobot [C]// Proceedings of the 48th IEEE Conference on Decision and Control. Shanghai, China: IEEE Computer Society, 2009: 1770-1775.
[14] BERGERMAN M, XU Y. Robust control of underactuated manipulators: analysis and implementation [C]// IEEE International Conference on Systems, Man, and Cybernetics. San Antonio, TX, USA, 1994: 925-930.
[15] QIAN D W, LIU X J, YI J Q. Robust sliding mode control for a class of underactuated systems with mismatched uncertainties [J]. Journal of Systems and Control Engineering, 2009, 223(6): 785-795.
[16] O’FLAHERTY RW, SANFELICE R G, TEEL A R. Hybrid control strategy for robust global swing-up of the pendubot [C]// American Control Conference. Seattle, USA, 2008: 1424-1429.
[17] XIN X, KANEDA M. A robust control approach to the swing up control problem for Acrobot [C]// Proceedings of 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems. Maui, 2001: 1650-1655.
[18] YAZICI A, KARAMANCIOGLU A. Robust stabilization of acrobot by using its real structured uncertainty model [C]// Proceedings of 2nd International Conference on Recent Advances in Space Technologies. Istanbul, Turkey, 2005: 265-270.
[19] ORLOV Y, AGUILAR L T, ACHO L. Model orbit robust stabilization (MORS) of pendubot with application to swing up control [C]// Proceedings of IEEE CDC and the European Control Conference. Seville, Spain, 2005: 6164-6169.
[20] IWASKI T, SKELTON R. All controllers for the general H∞ control problems: LMI existence conditions and statespace formulas [J]. Automatica, 1994, 30(8): 1307-1317.
[21] TODA M. An H∞ control-based approach to robust control of mechanical systems with oscillatory bases [J]. IEEE Transactions on Robotics and Automation, 2004, 20(2): 283-296.
[22] YEON J S, PARK J H. Practical robust control for flexible joint robot manipulators [C]// Proceedings of 2008 IEEE International conference on Robotics and Automation. Pasadena, CA, USA, 2008: 3377-3382.
[23] JIANG W P, GE W. Modeling and H∞ robust control for mobile robot [C]// Proceedings of 2008 IEEE Conference on Robotics, Automation and Mechatronics. Chengdu, China, 2008: 1108-1112.
[24] GAHINET P, APKARIAN P. A linear matrix inequality approach to H1 control [J]. International Journal Robust and Nonlinear Control, 1994, 4(4): 421-448.
[25] GAHINET P, NEMIROVSKII A, LAUB A, CHILALI M. The LMI Control Toolbox [C]// Proceedings of the 33rd IEEE Conference on Decision and Control. Lake Buena Vista, USA, 1994: 2038-2041.
(Edited by YANG Bing)
Foundation item: Projects(61074112, 60674044) supported by the National Natural Science Foundation of China
Received date: 2011-07-15; Accepted date: 2011-09-23
Corresponding author: LAI Xu-zhi, Professor, PhD; Tel: +86-731-88836091; E-mail: xuzhi@csu.edu.cn