DOI: 10.11817/j.ysxb.1004.0609.2020-37408
7A85铝合金塑性变形过程位错密度模型
胡建良1, 2,焦子腾1,金 淼1,王 欢1,黄始全2
(1. 燕山大学 机械工程学院,秦皇岛 066004;
2. 中南大学 高性能复杂制造国家重点实验室,长沙 410083)
摘 要:通过等温热压缩试验,研究7A85铝合金在应变速率为0.001~0.5 s-1、变形温度为250~450 ℃条件下的流变行为。结果表明,7A85铝合金在塑性变形过程中,流变应力达到峰值前后的软化机制不同。在流变应力达到峰值应力前,加工硬化作用占主导地位,软化机制主要是材料内部位错的交滑移,动态回复不明显。当流变应力达到峰值后,材料内部发生明显的动态回复和再结晶现象。基于流变应力达到峰值前后的软化机制不同,建立了“两阶段”式Kocks-Mecking(K-M)位错密度模型来描述7A85铝合金塑性变形过程的位错密度演变规律,并验证了模型的准确性。
关键词:7A85铝合金;塑性变形;位错密度模型;位错演变
文章编号:1004-0609(2020)-06-1263-07 中图分类号:TG146.2 文献标志码:A
作为新一代Al-Zn-Mg-Cu超高强铝合金[1-2],7A85铝合金因其具有高比强度、高淬透性和高损伤容限等特点,被广泛应用于航空航天、武器装备等领域[3-5]。在材料成形过程中,位错密度不仅影响铝合金塑性变形过程的流变行为,而且还影响材料内部晶粒组织、析出相等微观组织的演化行为[6-7]。因此,有必要构建能准确描述7A85铝合金塑性变形过程位错演变规律的模型,从而为制定铝合金的热变形工艺提供理论依据。
目前,基于加工硬化和动态软化效应的Kocks- Mecking(K-M)位错密度模型[8]被广泛应用于金属塑性变形过程中位错演化规律的研究。王晓强等[9]研究40Cr高速冷滚打成形过程的K-M位错密度模型,并验证了模型的准确性;杜大鹏[10]利用K-M位错密度模型准确地描述了纯铜在冷变形过程中的位错密度的演变规律。高志刚等[11]基于K-M位错密度模型研究了TC18钛合金热变形过程中的加工硬化行为。CHRISTOPHER等[12]通过K-M位错密度模型研究了改进的9Cr-1Mo钢在焊后热处理条件下的加工硬化行为。HE等[13]借助K-M位错密度模型对ZK60合金的应变硬化行为进行了建模,并构建了一种考虑动态再结晶的本构模型来预测合金的流变应力。
K-M位错密度模型通过引入加工硬化和动态软化系数来描述材料变形过程的位错演变规律,但材料在流变应力达到峰值前后其软化机制并不相同,故其加工硬化系数和动态软化系数也应有所差异。因此,本文作者拟基于K-M位错密度模型,建立一种“两阶段”式位错密度模型来描述7A85铝合金在塑性变形过程位错密度的演变规律,为铝合金宏微观组织及性能预测提供理论依据。
1 实验
在Gleeble-3800型热模拟试验机上进行7A85铝合金的等温压缩实验,实验所用材料的化学成分如表1所示。在d 8 mm×12 mm试样的两端涂抹高温润滑剂并粘贴石墨片以减小压头与试样端面的摩擦力。将试样以10 ℃/s的速度分别加热到250、300、350、400、450 ℃,保温5 min后再以0.001、0.005、0.01、0.05、0.1、0.5 s-1的应变速率进行热压缩实验,变形量为60%。
表1 7A85铝合金的化学成分
Table 1 Chemical composition of 7A85 aluminum alloy (mass fraction, %)

2 结果与分析
2.1 铝合金塑性变形过程位错演变规律分析
图1所示为7A85铝合金在不同热变形条件下的真应力-应变曲线。由图1可以看出,在塑性变形初期,流变应力随应变的增加迅速增大,这是由于塑性变形导致位错大量增殖,位错相互缠结、交割导致位错运动受阻,产生加工硬化。当流变应力达到峰值后,材料发生明显的软化现象,在低温变形条件下(≤350 ℃),流变应力随应变增加而减小并最终达到稳态值。这是由于随着应变的增加,由位错增殖导致的形变储能增加到临界值时,推动合金内部位错的对消和位错结构的重新排列,如形成位错胞和亚晶界[14],使位错向着低能结构转化,直到位错的回复和增殖达到平衡。当变形温度较高时(≥400 ℃),在变形初期大量增殖的位错为再结晶提供驱动力,当位错密度达到临界值后,合金内部发生动态再结晶,导致位错大量减少,最终位错消减和位错增殖的速度趋于平衡,流变应力进入稳态阶段。
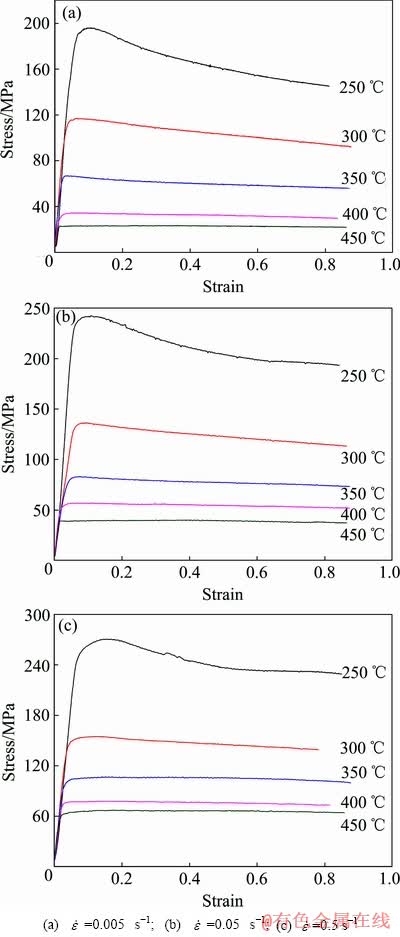
图1 不同应变速率下7A85铝合金的真应力-应变曲线
Fig. 1 True stress-strain curves of 7A85 aluminum alloy at different strain rates
2.2 K-M位错密度模型构建
KOCKS和MECKING通过研究加工硬化和动态软化过程对合金内部位错密度演变的影响规律,提出了描述金属塑性变形过程中位错密度演变的物理模型,即K-M位错密度模型[8, 15]。模型假设位错密度直接控制材料的塑性变形过程,即加工硬化引起的位错密度变化和位错密度ρ1/2呈线性关系,而动态软化引起的位错密度减小量和位错密度ρ呈线性关系:
 (1)
(1)
式中:k1、k2分别是材料的加工硬化系数和动态软化系数。
传统K-M位错密度模型通过一组硬化、软化系数来描述变形全程的位错变化,但材料在流变应力达到峰值前后其软化机制并不相同,故其硬化、软化系数也应有所差异。研究表明[13, 16],在流变应力达到峰值应力前,其加工硬化作用占主导地位,软化机制主要是材料内部位错交滑移的作用,动态回复不明显,材料组织内部位错密度随着应变的增加而明显增加。当流变应力达到峰值应力后,动态软化效应明显,其主要是由于形变储能推动材料内部产生明显的动态回复过程[17],并且当满足再结晶温度条件时,形变储能可以为动态再结晶提供驱动力,此时动态再结晶和回复为主要软化机制。基于这种差异,本文作者采用“两阶段”式位错密度模型来描述7A85铝合金在塑性变形过程的位错密度演变规律。
在流变应力达到峰值前,对式(1)积分得到位错密度的表达式为
 (2)
(2)
式中:ρ0为初始位错密度,当流变应力达到峰值时, ,由式(2)可得
,由式(2)可得
 (3)
(3)
式中: 为材料在变形过程中应力达到峰值时的位错密度。经典Taylor关系[18]如下:
为材料在变形过程中应力达到峰值时的位错密度。经典Taylor关系[18]如下:
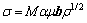 (4)
(4)
式中:M为泰勒因子;μ为剪切模量;b为柏氏矢量值; 为常数,一般取值0.5左右。
为常数,一般取值0.5左右。
结合式(2)~(4),则有
 ,
, <
< (5)
(5)
当流变应力从峰值达到稳态阶段,用 、
、 分别表示此阶段材料的加工硬化系数和动态软化系数,由式(1)积分,可得此阶段位错密度表达式为
分别表示此阶段材料的加工硬化系数和动态软化系数,由式(1)积分,可得此阶段位错密度表达式为
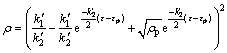 (6)
(6)
同理,由Taylor关系可得
 ,
,
 ≥
≥ (7)
(7)
2.2.1 材料常数确定
目前,包含Z参数的Arrhenius方程被广泛应用于描述合金的流变行为[19-20],其表达式如下:
低应力水平下( <0.8),
<0.8),
 (8)
(8)
高应力水平下( >1.2),
>1.2),
 (9)
(9)
所有应力水平,
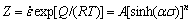 (10)
(10)
式中:A1、A2、A、n、 和β为与变形温度无关的材料常数;A为结构因子,s-1;n为应力指数;
和β为与变形温度无关的材料常数;A为结构因子,s-1;n为应力指数; 为应力水平参数,mm2/N;Q为激活能;R为摩尔气体常数;T为温度;β及n1之间满足:
为应力水平参数,mm2/N;Q为激活能;R为摩尔气体常数;T为温度;β及n1之间满足: 。β和n1可通过
。β和n1可通过 与
与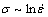 的线性关系获得(如图2所示):n1=7.21,β=0.115 MPa-1,
的线性关系获得(如图2所示):n1=7.21,β=0.115 MPa-1, =0.016 MPa-1。
=0.016 MPa-1。
对式(10)两边同时取自然对数并求偏微分,可得
 (11)
(11)
对 数据进行一元线性回归分析,求得斜率的平均值并根据式(11)得到7A85铝合金的激活能Q=313 kJ/mol。
数据进行一元线性回归分析,求得斜率的平均值并根据式(11)得到7A85铝合金的激活能Q=313 kJ/mol。

图2  与
与 的关系
的关系
Fig. 2 Relationship between stress and strain rate
2.2.2 特征应力应变模型回归
对式(10)两边取对数,将不同变形条件下的峰值应力和稳态应力代入,绘制 与
与 的关系图(见图3)。对图3中的数据进行一元线性回归分析,将所得到的材料常数代入式(10),即可得到7A85铝合金峰值应力与稳态应力模型:
的关系图(见图3)。对图3中的数据进行一元线性回归分析,将所得到的材料常数代入式(10),即可得到7A85铝合金峰值应力与稳态应力模型:

 (12)
(12)

 (13)
(13)
研究表明[21],峰值应变可用包含Z参数的函数表示,如式(14)所示,其中k、m为待定常数。

图3  ~
~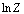 与
与 ~
~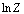 之间的关系
之间的关系
Fig. 3 Relationship between  and
and 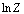
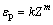 (14)
(14)
将不同变形条件下的峰值应变代入模型进行线性回归,得到峰值应变 的模型为
的模型为
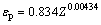 (15)
(15)
由于流动应力曲线上的初始应力不明显,根据有关学者研究,初始应力可取当应变达到0.2%时的应力值[22],初始应力σ0的数学模型可用式(16)表示,拟合实验数据,得到初始应力模型,如式(17):
 (16)
(16)
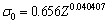 (17)
(17)
2.2.3 动态软化系数确定
根据Taylor关系,结合式(2),得到式(18),利用下式即可求取不同变形条件下的动态软化系数:
 (18)
(18)
其中,动态软化系数可用如下模型表示:
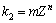 (19)
(19)
式中:m、n为常数,对其两边取对数并绘制 ~
~ 和
和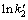 ~
~ 的关系图,如图4所示,根据拟合结果,得到k2、
的关系图,如图4所示,根据拟合结果,得到k2、 的表达式为
的表达式为
 (20)
(20)
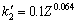 (21)
(21)
综上所述,7A85铝合金塑性变形过程的“两阶段”式K-M位错密度模型如下:
 (22)
(22)
其中

 ;
;

 ;
;
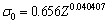 ;
;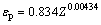 ;
;
 ;
;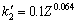 。
。
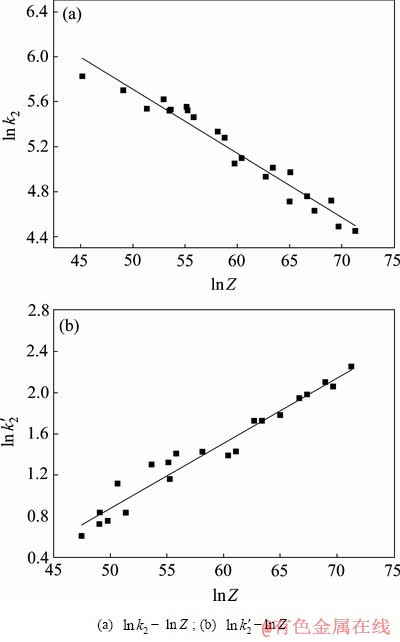
图4  ~
~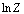 和
和 ~
~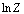 的线性关系
的线性关系
Fig. 4 Relationship between  ,
,  and lnZ
and lnZ
2.3 模型验证
结合Taylor关系(式(4))与实验所获流变应力曲线,得到7A85铝合金在不同变形条件下的位错密度变化曲线,如图5实验值曲线所示。通过位错密度模型预测的不同变形条件下7A85铝合金的位错密度值如图5预测值所示。由图5可知,无论在初始变形阶段还是在稳态阶段,本文所建立的“两阶段”式位错密度模型与实验所获的位错密度变化曲线的吻合程度都较高,说明“两阶段”式位错密度模型能准确描述7A85铝合金在塑性变形过程的位错密度演变规律。

图5 不同变形条件下的位错密度预测值与实验值曲线
Fig. 5 Comparison between experimental and predicted dislocation density at different strain rates
根据“两阶段”式位错密度模型对铝合金的流变应力进行了预测,并与实验所获流变应力曲线进行对比,如图6所示。结果表明,本文所建立的位错密度模型可以准确预测7A85铝合金塑性变形过程中的流变行为,进一步验证了该模型的可信度。
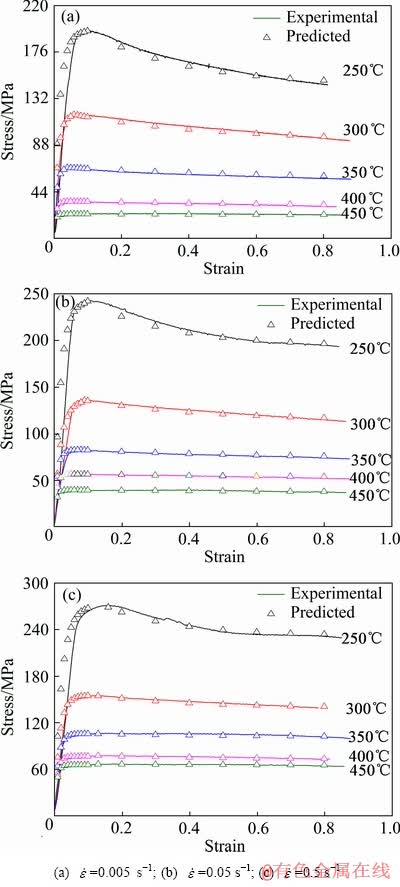
图6 不同变形条件下流变应力预测值与实验曲线对比
Fig. 6 Comparison between experimental and predicted flow stress at different strain rates
3 结论
1) 7A85铝合金在塑性变形过程中同时存在加工硬化和动态软化现象,应力达到峰值前后其软化机制不同,在流变应力达到峰值应力前,其加工硬化作用占主导地位,软化机制主要是材料内部位错交滑移的作用,动态回复不明显。在流变应力达到峰值应力后,材料内部发生明显的动态回复和再结晶现象。
2) 基于K-M模型,建立了能准确描述7A85铝合金在塑性变形过程的位错密度演变规律的“两阶段”式位错密度模型,并验证了该模型的准确性。
REFERENCES
[1] 仇琍丽, 高文理, 陆 政, 冯朝辉. 7A85铝合金的热压缩流变行为与显微组织[J]. 材料工程, 2016, 44(1): 33-39.
QIU Li-li, GAO Wen-li, LU Zheng, FENG Zhao-hui. Flow behavior and microstructure of 7A85 aluminum alloy during hot compression[J]. Journal of Materials Engineering, 2016, 44(1): 33-39.
[2] 柏 璠, 高文理, 何正林, 陆 政, 冯朝辉. 时效工艺对7A85铝合金力学和晶间腐蚀性能的影响[J]. 中国有色金属学报, 2016, 26(5): 957-963.
BAI Fan, GAO Wen-li, HE Zheng-lin, LU Zheng, FENG Zhao-hui. Effect of ageing processes on mechanical properties and intergranular corrosion of 7A85 aluminum alloy[J]. The Chinese Journal of Nonferrous Metals, 2016, 26(5): 957-963.
[3] 贾逢博, 易幼平, 黄施全, 李 云. 7A85铝合金热压缩流变行为与本构方程研究[J]. 热加工工艺, 2010, 39(16): 19-21.
JIA Feng-bo, YI You-ping, HUANG Shi-quan, LI Yun. Study on flow behavior and constitutive equation of 7A85 aluminum alloy during hot compression[J]. Material & Heat Treatment, 2010, 39(16): 19-21.
[4] 姚晓红, 张 林, 高文理, 田林海. 时效状态对7A85高强铝合金力学性能和晶间腐蚀性能的影响[J]. 稀有金属材料与工程, 2013, 42(12): 2581-2585.
YAO Xiao-hong,ZHANG Lin,GAO Wen-li,TIAN Lin-hai. Effect of aging treatment on mechanical and intergranular corrosion properties of 7A85 high strength aluminum alloy[J]. Rare Metal Materials and Engineering, 2013, 42(12): 2581-2585.
[5] 陈送义, 陈康华, 董朋轩, 叶升平, 黄兰萍, 阳代军. 双级时效对7085铝合金组织和性能的影响[J]. 中国有色金属学报, 2015, 25(10): 2688-2694.
CHEN Song-yi, CHEN Kang-hua, DONG Peng-xuan, YE Sheng-ping, HUANG Lan-ping, YANG Dai-jun. Effect of two-step aging on microstructure and properties of 7085 aluminum alloy[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(10): 2688-2694.
[6] LIU Sheng-dan, LI Qun, LIN Hua-qiang, SUN Lin, LONG Tao, YE Ling-ying, DENG Yun-lai. Effect of quench-induced precipitation on microstructure and mechanical properties of 7085 aluminum alloy[J]. Materials & Design, 2017, 132: 119-128.
[7] LIU Sheng-dan, LIU Wen-jun, ZHANG Yong, ZHANG Xin-ming, DENG Yun-lai. Effect of microstructure on the quench sensitivity of AlZnMgCu alloys[J]. Journal of Alloys & Compounds, 2010, 507(1): 53-61.
[8] MECKING H, KOCKS U F. Kinetics of flow and strain- hardening[J]. Acta Metallurgica, 1981, 29(11): 1865-1875.
[9] 王晓强, 崔凤奎, 燕根鹏, 李玉玺. 40Cr冷滚打成形中位错密度变化研究[J]. 中国机械工程, 2013(16): 2248-2252.
WANG Xiao-qiang, CUI Feng-kui, YAN Gen-peng, LI Yu-xi. Study on dislocation density change during cold roll-beating of 40Cr[J]. China Mechanical Engineering, 2013(16): 2248-2252.
[10] 杜大鹏. 基于位错密度的流动应力模型的研究[D]. 上海: 上海交通大学, 2010: 50-51.
DU Da-peng. The study on flow stress model based on dislocation density[D]. Shanghai: Shanghai Jiao Tong University, 2010: 50-51.
[11] 高志刚, 郭鸿镇, 苗小浦, 姚泽坤. 协同K-M和E-M准则的TC18钛合金高温变形加工硬化行为[J]. 材料热处理学报, 2015, 36(2): 223-229.
GAO Zhi-gang, GUO Hong-zhen, MIAO Xiao-pu, YAO Ze-kun. Work-hardening behavior of TC18 titanium alloy during hot processing associating K-M and E-M criterion[J]. Transactions of Materials and Heat Treatment, 2015, 36(2): 223-229.
[12] CHRISTOPHER J, CHOUDHARY B K, MATHEW M D, JAYAKUMAR T. Applicability of the one-internal-variable Kocks-Mecking approach for tensile flow and work hardening behaviour of modified 9Cr-1Mo steel[J]. Materials Science and Engineering A, 2013, 575(13): 119-126.
[13] HE Yun-bin, PAN Qing-li, CHEN Qin, ZHANG Zhi-ye,LIU Xiao-yan,LI Wen-bin. Modeling of strain hardening and dynamic recrystallization of ZK60 magnesium alloy during hot deformation[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(2): 246-254.
[14] LIU Xin-gang, HAN Shuang, CHEN Lei, YANG Shuai, JIN Miao, GUO Bao-feng, MAO Tian-hong. Flow behavior and microstructural evolution of 7A85 high-strength aluminum alloy during hot deformation[J]. Metallurgical & Materials Transactions A, 2017, 48(5): 1-13.
[15] KUGLER G, TURK R. Modeling the dynamic recrystallization under multi-stage hot deformation[J]. Acta Materialia, 2004, 52(15): 4659-4668.
[16] SUN Ming-yue, HAO Lu-han, LI Shi-jian, LI Dian-zhong, LI Yi-yi. Modeling flow stress constitutive behavior of SA508-3 steel for nuclear reactor pressure vessels[J]. Journal of Nuclear Materials, 2011, 418(1): 269-280.
[17] 顾 伟, 李静媛, 王一德, 卢继延, 周玉焕. 淬火弹性应变能对7050铝合金时效亚晶界演变的影响[J]. 中国有色金属学报, 2014, 24(9): 2257-2263.
GU Wei, LI Jing-yuan, WANG Yi-de, LU Ji-yan, ZHOU Yu-huan. Effect of quenching elastic strain energy on evolution of sub-grain boundaries in 7050 aluminum alloy during aging[J]. The Chinese Journal of Nonferrous Metals, 2014. 24(9): 2257-2263.
[18] ZHANG Fan, HUANG Yong-gang, HWANG Keh-Chih. The indenter tip radius effect in micro-and nanoindentation hardness experiments[J]. Acta Mechanica Sinica, 2006, 22(1): 1-8.
[19] WU H, WEN S P, HUANG H, WU X L., GAO K Y, WANG W, NIE Z R. Hot deformation behavior and constitutive equation of a new type Al-Zn-Mg-Er-Zr alloy during isothermal compression[J]. Materials Science and Engineering A, 2016, 651: 415-424.
[20] CHEN Song-yi, CHEN Kang-hua, PENG Guo-sheng, CHEN Xue-hai, CENG Qing-hua. Effect of heat treatment on hot deformation behavior and microstructure evolution of 7085 aluminum alloy[J]. Journal of Alloys & Compounds, 2012, 537: 338-345.
[21] 张佩佩, 隋大山, 齐 珂, 崔振山. 316LN钢高温流动应力与动态再结晶模型[J]. 塑性工程学报, 2014, 21(1): 44-51.
ZHANG Pei-pei, SUI Da-shan, QI Ke, CUI Zhen-shan. Modeling of flow stress and dynamic recrystallization for 316LN steel during hot deformation[J]. Journal of Plasticity Engineering, 2014, 21(1): 44-51.
[22] 齐 珂. 核电用钢316LN动态再结晶行为实验研究与数值模拟[D]. 上海: 上海交通大学, 2014: 32-33.
QI Ke. Experimental and numerical study on dynamic recrystallization of 316LN nuclear power steel[D]. Shanghai: Shanghai Jiao Tong University, 2014: 32-33.
Dislocation density model of 7A85 aluminum alloy during plastic deformation process
HU Jian-liang1, 2, JIAO Zi-teng1, JIN Miao1, WANG Huan1, HUANG Shi-quan2
(1. College of Mechanical Engineering, Yanshan University, Qinhuangdao 066004, China;
2. State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410083, China)
Abstract: The flow behavior of 7A85 aluminum alloy was studied by isothermal compression test at the strain rate range of 0.001-0.5 s-1 and temperature range of 250-450 ℃. The results show that, during the plastic deformation process, the softening mechanism of the flow stress is different before and after the peak flow stress of the 7A85 aluminum alloy. Before the flow stress reaches the peak, the work hardening is dominant and the main softening mechanism is the cross-slip of the dislocation inside the material, whereas, the dynamic recovery is not obvious. After the flow stress reaches the peak, the obvious dynamic recovery and recrystallization occur inside the material. Based on the difference of the softening mechanism before and after the peak stress, a “Two-stage” Kocks-Mecking (K-M) dislocation density model was established to describe the dislocation evolution during the plastic deformation process of 7A85 aluminum alloy, and the accuracy of the model was verified.
Key words: 7A85 aluminum alloy; plastic deformation; dislocation density model; dislocation evolution
Foundation item: Project(Kfkt2017-07) supported by the State Key Laboratory Program of High Performance Complex Manufacturing, China; Project(B980) supported by Doctor Foundation of Yanshan University, China
Received date: 2018-07-27; Accepted date: 2018-10-16
Corresponding author: JIN Miao; Tel: +86-335-8056775; E-mail: jmiao@ysu.edu.cn.
(编辑 李艳红)
基金项目:高性能复杂制造国家重点实验室开放课题项目(Kfkt2017-07);燕山大学博士基金资助项目(B980)
收稿日期:2018-07-27;修订日期:2018-10-16
通信作者:金 淼,教授,博士;电话:0335-8056775;E-mail:jmiao@ysu.edu.cn