J. Cent. South Univ. Technol. (2008) 15(s1): 017-020
DOI: 10.1007/s11771-008-305-3
Dynamic analysis of polymeric fluid in shear flow for dumbbell model with internal viscosity
YANG Xiao-dong(杨晓东)1, R. V. N. MELNIK2
(1. Department of Engineering Mechanics, Shenyang Institute of Aeronautical Engineering,
Shenyang 110136, China;
2. Mathematical Modelling and Computational Sciences, Wilfrid Laurier University,
Waterloo, Ontario, Canada N2L 3C5)
Abstract: The dynamic analysis of semi-flexible polymers, such as DNA molecules, is an important multiscale problem with a wide range of applications in science and bioengineering. In this contribution, a dumbbell model with internal viscosity was studied in steady shear flows of polymeric fluid. The tensors with moments other than second moment were approximated in the terms of second moment tensor. Then, the nonlinear algebraic equation of the second moment conformation tensor was calculated in closed form. Finally, substituting the resulting conformation tensor into the Kramers equation of Hookean spring force, the constitutive equations were obtained. The shear material properties were discussed for different internal viscosities and compared with the results of Brownian dynamics simulation.
Key words: dynamic simulation; polymeric fluid; internal viscosity; shear thinning
1 Introduction
The dynamics of polymeric fluids is an important multiple time scale problem, which involves quick speed of small solvent molecules, fast movement of atomic particles that constitute the polymers and slow orientation of the polymer deformation[1]. The simplest, albeit useful in applications, model for polymer solutions is the Hookean dumbbell model proposed by KUHN[2], where a polymer molecule in dilute solution is modeled by two beads connected by a spring force. The mathematical simplification of this model has contributed a lot to developing constitutive equations and investigating solution of polymer fluid dynamics problems[1-3]. To match the empirical results, a few additions have been incorporated into the standard dumbbell model. Finitely extensible nonlinear elastic (FENE) property and internal viscosity of the spring are among them. For both cases, the governing equations of conformation tensors are nonlinear and have no closed form solutions without approximations.
Brownian dynamic simulation has been used widely in the computation of the governing equation for FENE dumbbell model. Generally speaking, it can lead to accurate results compared to the approximate theoretical method[4-6]. Brownian dynamic simulation is not a good method to explain the physical properties. On the other hand, simulation is sometimes time consuming. Analytical method makes the explanation of the physical phenomena more straightforward. Some closure forms of the conformation tensor equation make the governing equation analytically solvable. YANG and MELNIK proposed an approximation scheme to solve the governing equation for polymeric fluids for dumbbell model with internal viscosity[7-8].
In this paper, the approximation scheme was used to explain the dynamics of the polymeric fluid in shear flows. Based on the analytical solutions, the material properties of the polymeric fluid in steady-state shear flow were discussed. The shear shinning phenomenon was found and the results were compared with those obtained by Brownian dynamics simulation. The contribution of the internal viscosity was also analyzed with the presented numerical examples.
2 Constitutive model
The polymers of bead-spring-bead dumbbell model in a Newtonian solvent with viscosity ηs are presumed that there is no interaction between the beads. Let ζ denote the viscous drag coefficient due to the resistance of the flow. For the dumbbell model with internal viscosity(IV), the spring force is a function of the configuration vector and configuration velocity. A force law can be expressed in the following form:
 (1)
(1)
where 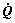 is the length of vector Q, H is the spring coefficient of the dumbbell model and K is a constant denoting the measurement of the IV. The dot means differentiation with respect to time. Substituting Eqn.(1) and the equation of motion of one bead into the continuity equation yields diffusion equation[3]
is the length of vector Q, H is the spring coefficient of the dumbbell model and K is a constant denoting the measurement of the IV. The dot means differentiation with respect to time. Substituting Eqn.(1) and the equation of motion of one bead into the continuity equation yields diffusion equation[3]
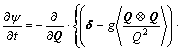
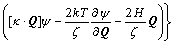 (2)
(2)
where ψ is the configuration distribution function of Q, δ is unit matrix; g=2ε/(1+2ε) and ε is the relative internal viscosity, ε=K/ζ, which ranges from zero to infinity. For g=0, Eqn.(2) recovers the form of the diffusion equation for Hookean dumbbells without IV.
The second moment conformation tensor is of the most interest when calculating the stress tensor. The governing equation of conformation tensor can be developed by multiplying the diffusion equation by the dyadic product Q?Q and integrating over the entire configuration space:
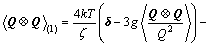
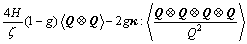 (3)
(3)
The subscript (1) denotes convected derivative. We can not calculate the second moment tensor because there are other moment terms, e.g. <(Q?Q)/Q2> and . In order to put the governing equation into solvable form, the high order terms can be approximated as follows:
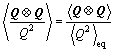 (4)
(4)
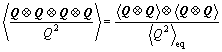 (5)
(5)
These two equations are key approximations to make the governing equation analytically solvable. Eqn.(6) is similar to the Perterlin approximation used in FENE dumbbell model. Using the approximation Eqns.(4) and (5), we cast the governing Eqn.(3) into:
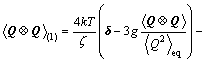
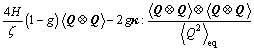 (6)
(6)
Eqn.(6) is a nonlinear algebraic equation of if all the time-dependent terms are neglected in the steady state flow case. In the next section, we will seek a closed form solution to this governing equation, followed by the material properties discussion in the case of steady state shear flow.
3 Results and examples
3.1 Material coefficients in closed form
Now we consider the steady state shear flow with velocity vector
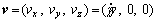 (7)
(7)
where 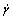 is the shear rate. The transpose of velocity vector gradient is
is the shear rate. The transpose of velocity vector gradient is
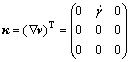 (8)
(8)
The average value of the square of the end-to-end distance in equilibrium for the Hookean dumbbell model in shear flow with shear rate 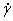 is
is
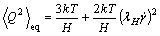 (9)
(9)
where λH is the time constant, λH=ζ/(4H). For conveni- ence, we introduce notation for the conformation tensor
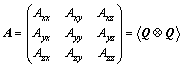 (10)
(10)
and its convected differentiation in steady state
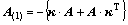 (11)
(11)
Substituting Eqns.(7)-(11) into Eqn.(6) yields
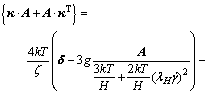
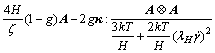 (12)
(12)
For convenience, we can use the Kramers equation of stress tensor for spring model
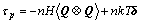 (13)
(13)
In this model, the stress tensor does depend on the internal viscosity force as indicated by WEDGEWOOD[9]. Substituting Eqns.(10) into (13), we obtain the stress tensor for spring model
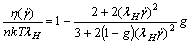 (14)
(14)
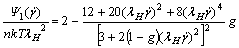 (15)
(15)
 (16)
(16)
If we let g=0 in Eqns.(14-16), the material properties of linear Hookean dumbbell model for shear flow case can be recovered.
3.2 Examples
According to Eqns.(14-16), we can calculate the material properties for different internal viscosities. Fig.1 demonstrates the comparison between our approximate solutions with Brownian dynamics simulation data where the internal viscosity g=0.1 is chosen[9]. In Fig.1, the solid lines denote our approximate results for the material coefficients and the asterisks denote the data obtained by Brownian dynamics simulation. For both viscosity and first-normal stress coefficients, we have demonstrated good agreements.
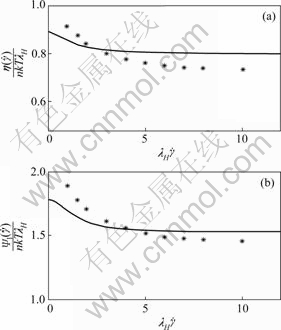
Fig.1 Comparison analytical results with Brownian dynamics simulation: (a) Viscosity coefficient; (b) First-normal stress coefficient
With the increase of the shear rates, the material coefficients decrease substantially, which is the characteristic of shear thinning. This phenomenon demonstrated in the comparison plots verifies the efficiency of the approximation method which we proposed in this contribution. The contributions of the internal viscosity have been presented for the three material properties, illustrated in Fig.2. It can be concluded that the internal viscosity explains the pheno- menon of shear thinning and higher internal viscosity makes stronger shear thinning. This phenomenon has been found by WEDGEWOOD and others using the integration method.
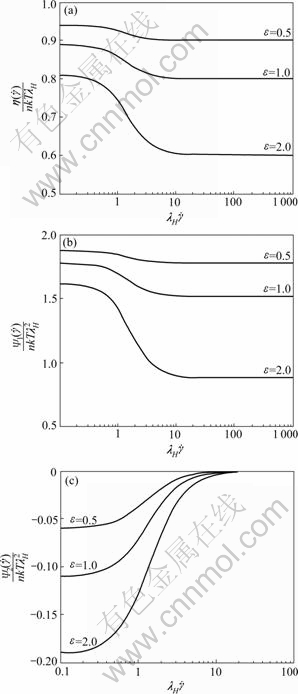
Fig.2 Contribution of IV: (a) Viscosity coefficient; (b) First- normal stress coefficient; (c) Second-normal stress coefficient
4 Conclusions
1) A set of approximated analytical solutions for the dumbbell model with internal viscosity without integration of the Gaussian distribution nor any numerical computation are proposed.
2) Concise equations in this study can predict the material coefficients of the complex flow qualitatively and rather quantitatively, and the shear thinning phenomena are described well with the results deduced from the dumbbell model with internal viscosity.
References
[1] BIRD R B, et al. Dynamics of polymer liquids (Vol. 2): Kinetic theory [M]. New York: John Wiley & Sons, Inc. 1987.
[2] KUHN W. ?ber die gestalt fadnf?miger moleküle in l?sungen [J]. Kolloid Z, 1934, 68: 2-11.
[3] BIRD R B, WIEST J M. Constitutive equations for polymeric liquids [J]. Annual Review of Fluid Mechanics, 1995, 27: 169-193.
[4] HUR J S, SHAQFEH E S G. Brownian dynamics simulations of single DNA molecules in shear flow [J]. Journal of Rheology, 2000, 44: 713-741.
[5] LOZINSKI A, CHAUVIERE C. A fast solver for Fokker-Planck equation applied to viscoelastic flows calculations: 2D FENE model [J]. Journal of Computational Physics, 2003, 189: 607-625.
[6] HU X, DING Z, LEE L J. Simulation of 2D transient viscoelastic flow using the CONNFFESSIT approach [J]. Journal of Non-Newtonian Fluid Mechanics, 2005, 127: 107-122.
[7] YANG X D, MELNIK R V N. A new constitutive model for the analysis of semiflexible polymers with internal viscosity [J]. Lecture Notes on Computer Science, 2007, 4487: 834-841.
[8] YANG X D, MELNIK R V N. Effect of internal viscosity on Brownian dynamics of DNA molecules in shear flow [J]. Computational Biology and Chemistry, 2007, 31: 110-114.
[9] WEDGEWOOD L E. Internal viscosity in polymer kinetic theory: Shear flows [J]. Rheologica Acta, 1993, 32: 405-417.
(Edited by CHEN Wei-ping)
Foundation item: Project(10702045) supported by the National Natural Science Foundation of China
Received date: 2008-06-25; Accepted date: 2008-08-05
Corresponding author: YANG Xiao-dong, PhD; Tel: +86-24-86192560; E-mail: jxdyang@163.com