单轴拉应力下铝空位形成能和自扩散激活能的计算

臧冰¹，易丹青^{1, 2}，刘欢¹，江勇^{1, 2}，王斌^{1, 2}

(1. 中南大学 材料科学与工程学院，湖南 长沙，410083；

2. 中南大学 教育部有色金属材料科学与工程重点实验室，湖南 长沙，410083)

摘要：运用第一原理平面波赝势和NEB(Nudged Elastic Band)过渡态搜索的方法计算应力作用下铝的自扩散激活能，并结合Flynn的原子迁移动力学理论，研究应力下铝自扩散的各向异性。研究结果表明：[100]方向的应力增大铝的空位形成能，在6%的应变下铝的空位形成能增大了18%。应力对铝自扩散激活能的影响在不同方向具有不同特征：随着应力的增大，铝的自扩散激活能在[011]方向上减小，在[101]方向上增大。应力对铝自扩散各向异性的影响在不同计算方法下有相同的趋势，但影响程度不同。在相同应力下，[011]和[101] 2个方向自扩散激活能的差异在Flynn模型的计算结果中最大，考虑原子弛豫的Flynn模型的计算结果次之，第一性原理过渡态搜索的计算结果最小。

关键词：应力；Al；自扩散激活能；原子迁移动力学；第一原理过渡态搜索

中图分类号：TG111.6          文献标志码：A         文章编号：1672-7207(2013)06-2214-09

Calculation of vacancy formation energy and self-diffusion activation energy of aluminum under uniaxial tensile stress

ZANG Bing¹, YI Danqing^{1, 2}, LIU Huan¹, JIANG Yong^{1, 2}, WANG Bin^{1, 2}

(1. School of Materials Science and Engineering, Central South University, Changsha 410083, China;

2. Key Laboratory of Nonferrous Metal Materials Science and Engineering, Ministry of Education,Central South University, Changsha 410083, China)

Abstract: The self-diffusion activation energy of aluminum under stress was calculated by using the first principle pseudopotential plane wave method and NEB transition state search method. Combined with atomic migration dynamics theory, the anisotropy of the self-diffusion of aluminum under stress was also investigated. The results show that the vacancy formation energy of aluminum increases when the stress is applied, and it increases by 18% under the strain of 6%. The influences of the stress on the self-diffusion activation energy of aluminum are different under different diffusion directions. With the increase of the stress, the self-diffusion activation energy of aluminum decreases in [011] direction, and increases in [101] direction. The influences of the stress on the anisotropy of the self-diffusion calculated with different methods are the same, but the degrees of influence are different. Under the same stress, the ratio of activation energies in [011] and [101] direction is the largest when calculated with Flynn’s atomic migration dynamics theory method smaller with Flynn’s method with atomic relaxation and the smallest with first principle transition state search method.

Key words: stress; Al; self-diffusion activation energy; atomic migration dynamics theory; first principle transition state search method

在纯金属和合金中，扩散与晶界运动、相变、蠕变等有着强烈的联系。点缺陷(包括空位和溶质原子)能够在热涨落的作用下在晶体中作无规则扩散，也能在应力的作用下做定向的迁移，产生溶质原子(或空位)扩散的各向异性，从而对扩散控制的相变产生影响，在某些合金中产生“应力位向效应”。为了解释“应力位向效应”和研究清楚应力下的原子扩散过程，国内外学者在实验和理论上进行了大量工作^[1-7]。王宏伟等^[4]研究了外加应力对2E12铝合金时效行为的影响，认为外加应力能促进S相的析出，并产生明显的应力位向效应，并根据Flynn的原子迁移动力学理论得出应力下铝的自扩散激活能具有各向异性。曹素芳等^[5]研究了外加应力对Al-Cu-Mg-Ag合金时效行为的影响，发现在外加应力的影响下，Ω相产生应力位向效应。Ardell等^[6]利用原子迁移动力学理论研究了Ni-Al合金在应力下的扩散系数，计算得到150 MPa的压应力使原子扩散能力降低6%。目前应力对扩散行为影响的研究大都以原子动力学理论为基础，没有考虑应力下的原子弛豫等因素，影响了计算结果的可靠性。在第一性原理中引入应力的方法已经非常成熟^[7-9]，但未见应力下铝自扩散性质的报道。鉴于原子扩散动力学理论的局限性和第一性原理计算的精确性，本文作者从第一性原理出发，计算出应力下铝的自扩散激活能，同时与原子迁移动力学理论进行比较，更准确的得到应力对扩散行为的影响。

1  计算方法

基于密度泛函理论(DFT)的计算方法^[10]，从第一性原理出发，将晶体的多电子状态简化为Kohn-Sham方程，借助VASP(Vienna Ab-initio Simulation Package)^[11]软件包, 使用赝势和平面波基组，计算体系的电子密度、总能和空位形成能等。同时采用NEB(Nudged Elastic Band)^[12]方法研究点缺陷的迁移，寻找扩散路径上的鞍点，得到扩散激活势垒。第一性原理计算结果的适用温度是0 K，0 K以上温度下体系的扩散问题需要进行振动频率、振动熵等问题，在本文中不进行考虑。理想晶体采用2×2×2的32个铝原子超胞进行计算，将理想晶体中的一个铝原子去掉得缺陷晶体。扩散势垒计算过程中采用的过渡态是由初始态和最终态的原子位置等值差值得到。平面波函数截断能Ecut取500 eV；布里渊区采用Monhkorst-Pack特殊k网格点方法，计算采取9×9×9的k网格点。计算收敛设置为：总体能量变化为9.6×10^-3 kJ/mol，每个原子的受力小于0.1eV/nm。

图1  计算模型和应力方向

Fig. 1  Calculation models and stress applied in crystals

如图1所示，在无应力下，空位V向其周围8个近邻原子的扩散是等效的，施加[100]方向的应力后，由于应力对(100)晶面和(010)晶面间距的不同影响，扩散分为2种情况：与应力方向垂直的[011]，，和扩散方向和与应力方向成45°的[101]，，和扩散方向。为了研究方便，在两种扩散方向上分别选取一个方向作为研究对象，即空位向A位置扩散的[011]方向和空位向B位置扩散的[101]方向。为了研究应力是如何对扩散在不同方向产生不同的影响，本文进行应力下空位形成能和自扩散激活能的计算。

含有点缺陷的结构在缺陷周围会形成表面效应，用块体材料的计算参数进行计算可能会有误差。研究表明使用LDA和GGA赝势进行计算可以减小表面误差，并且选用LDA赝势的表面修正误差小于GGA赝势，故本工作采用局域密度近似(LDA)。

应力的引入是通过在应力方向，即a轴方向，引入一个单轴拉伸应变^[13]

               (1)

式中：l_ε为应变ε时晶胞a轴方向长度；l₀为初始晶胞在a轴方向的长度。同时利用第一性原理方法对原子结构进行弛豫，使系统在应力形变下达到能量最优结构。作用在整个系统上的应力可以根据Nielsen-Martin方法获得^[14]

                 (2)

其中：E_t为体系的总能；σ为应力；Ω为体系的体积。将理想铝晶体拉伸变形假设为弹性变形，不考虑塑性变形作用，一方面可以简化计算，另一方面可以与他人的弹性计算模型进行比较。Nielsen-Martin方法是使用总能对应变做偏微分的方法求得系统的应力，为了保证5%应变内的结果的准确性，应变取0~6%。在计算过程中不考虑泊松效应，在施加应力的每一步都使用上一步优化的结构进行弛豫。

2  计算结果与分析

2.1  不同应变下的应力

根据Nielsen-Martin方法，为了得到不同拉应变下对应的体系平均应力，首先将体系在不同的单轴拉伸应变下进行总能的计算，得到不同应变下的总能与无应变下的总能差，在这里只考虑了在低应变下的体系性质，应变取0~6%。如图1所示，随着应变的增大，理想体系的总能逐渐增大。用得到的应变-总能关系进行偏微分计算得到不同变形条件下对应的应力，如图2所示，在6%的应变范围以内，随着变形程度的增大，体系的应力逐渐增大，并且呈现弹性性质。

根据图2(b)中的应力应变关系，由下式

                 (3)

可以得到铝晶体的弹性模量，E_y=98 GPa，大于实验值69 GPa^[15]，这是由于LDA的“过束缚”(over-binding)效应，使用LDA计算的结果中晶格参数偏小，弹性模量偏大；同时计算的体系为理想晶体，没有缺陷，导致计算值大于实验值。在计算空位形成能、空位迁移能和自扩散激活能时，这里关心的是能量的差异，从后面得到的空位形成能等数值与实验值的比较可以看出，能量的差值比较准确，所以使用LDA赝势是合适的。

图2  不同应变下的体系总能差和应力

Fig. 2  Total energy difference under different strains and strain-stress curve

2.2  应力下的空位形成能、扩散势垒和自扩散激活能

含有点缺陷的结构，与缺陷近邻的原子存在一个真空层为原子间距的微小表面，进行总能计算时会将这个表面的能量包含在内，在缺陷周围会形成“表面效应”，用块体材料的计算参数进行计算会有误差，在计算空位形成能和迁移能的过程中一般要进行表面修正。研究表明使用LDA和GGA赝势进行计算可以减小表面误差。对于铝晶体来说，使用LDA(GGA)赝势计算空位形成能的表面修正值为0.06 eV(0.15 eV)，计算迁移能的表面修正值为0.02 eV(0.05 eV)^[16-17]。由于LDA的表面修正值很小，并且发现计算得到的空位形成能和迁移能与实验值误差很小，所以这里没有考虑表面修正。

空位形成能的计算公式为

          (4)

式中：E_d(ε)为含有一个空位的体系的总能；E_p(ε)为理想体系的总能；N为理想晶体的Al原子个数，理想体系和缺陷体系都经过了充分弛豫。计算结果表明：没有应力的条件下，铝的空位形成能为0.695 eV，与实验值0.67 eV^[18]基本吻合。如表1所示，当体系施加应力时，铝的空位形成能增大，并且随着应力的增加，空位形成能逐渐增大，在6%的应变条件下，铝的空位形成能为0.826 eV，与不施加应力相比增大了大约18%。

在[100]方向的单轴应力下，理想体系和含空位体系的总能都随着应力的增大而增大，由于其增加程度不同导致空位形成能不同，故用应力下体系的总能与无应力下体系的总能差表示其增加程度：

          (5)

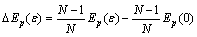     (6)

式中：△E_d(ε) 为应力下缺陷体系总能的增加；△E_p(ε)为应力下理想系统总能的增加。如图3所示，理想体系和含空位体系在应力下与非应力下总能差都随着应力的增大而增大，而理想体系的总能差增加的程度较小。由于理想体系在应力的作用下原子均处于点阵格点位置，体系的总能变化小，而施加应力的缺陷体系空位周围的原子在弛豫的作用下，原子向空位附近移动，偏离点阵格点位置，进一步增大了原子间距，体系总能变化相对大，而这就导致了空位形成能随着应力的增大而增大。

图3  应力下体系的总能与无应力下体系的总能差随应力的变化

Fig. 3  Total energy difference of configuration with stress and without stress as function of strain

使用第一原理NEB过渡态搜索的方法计算的空位迁移能结果如图4所示，无应力条件下铝的空位迁移能计算结果为0.608 eV，实验值为0.61 eV^[18]。由图4可知：在与应力方向垂直的[011]扩散路径和与应力方向不垂直的[101]扩散路径上，应力都使迁移能减小，但减小的程度不一样。在[011]扩散方向上，应力大幅度的减小了空位扩散迁移能，如表1所示，6%的应变使迁移能降低到0.408 eV，下降了33%；在[101]扩散方向上，6%的应变下迁移能为0.545 eV，下降了10%。

[100]方向的应力增大了铝的空位形成能，而减小了铝在[011]和[101]扩散方向上的空位迁移能，应力对自扩散激活能的影响是对空位形成能和空位迁移能的综合影响，自扩散激活能计算公式为：

              (7)

式中：Q为自扩散激活能；△H_f为空位形成能；△H_m为空位迁移能。

由表1的数据可知：无应力状态下铝的自扩散激活能为1.303 eV，与实验值1.31 eV^[18]吻合。应变对不同方向上的自扩散激活能产生了质的差异：随着应力的增大，[101]方向上自扩散激活能增大，[011]方向上的自扩散激活能减小，体现出了应力对扩散产生的各向异性。

图4  不同应力下铝在[011]和[101]方向上的自扩散能垒

Fig. 4  Self-diffusion barriers of aluminum in different diffusion directions

表1  应力下空位形成能、迁移能和自扩散激活能

Table 1  Vacancy formation energy, migration energy and self-diffusion activation energy of aluminum under stress

2.3  电荷密度

为了直观地理解原子间的键合作用性质，绘制了不同体系的电荷密度分布情况。图5所示为理想晶体的电子密度图。比较图5(a)和图5(b)可知，与无应力作用相比，应力作用下与应力方向垂直的Al(100)面的电子密度基本不变，并且铝原子周围的电荷密度是对称的。应力下Al(010)面的电子密度变化较大，如图5(d)所示，由于平行于此面的应力的作用，[100]方向的铝原子间距增大，Al—Al键的作用减弱，电子密度减小，同时原子间距的非对称变化造成铝周围电子密度的非对称性。为了将不同扩散方向的原子的电子密度进行比较，做同时含有A和B位置的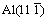面的电子密度图，如图5(c)和图5(d)所示，无应力作用下，Al—Al键的电子密度为32.8 e/nm³，应力使原本对称的电子密度发生方向性变化，在应力作用下，[011]方向的I区域的电子密度为32.6 e/nm³，与无应力作用的电子密度基本相等，[101]方向的III区域的电子密度和[110]方向的II区域的电子密度为30.9 e/nm³，与无应力状态相比减小了约6%，这是因为应力对不同方向的原子距离产生了影响。

图6所示为理想晶体在应力作用下临近铝原子距离的变化示意图。由图6可见：与应力方向垂直的晶面上的铝原子间距基本不变，与应力方向不垂直的晶面上的铝原子间距变大，由此导致了电子密度的相应变化。

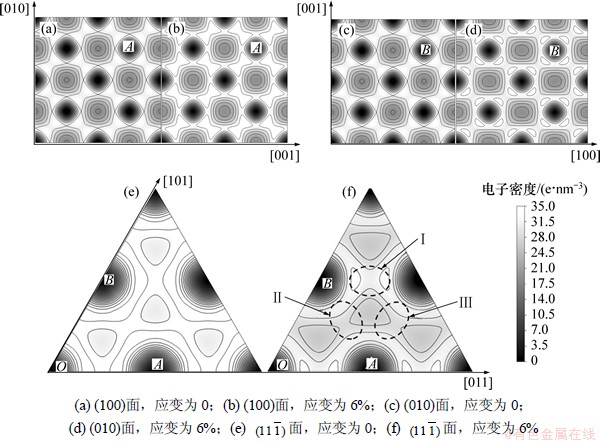
图5  理想晶体在不同面的电子密度

Fig. 5  Electron density of perfect crystal in different crystal planes

图6  理想晶体应力下铝近邻原子距离变化示意图

Fig. 6  Schematic of change in distance between the nearest neighbors of perfect system under stress

图7所示为含空位晶体在不同面的电子密度图，应力对含空位体系电子密度的影响与对理想体系的影响相似，从图7(a)和图7(b)的Al(100)面的电子密度可以看出：与无应力状态相比，应力下空位周围近邻铝原子之间的电子密度基本不变，为32.8 e/nm³，而(010)面(图7(c)和图7(d))的空位周围近邻铝原子之间的电子密度则变化较大，从32.8 e/nm³减小到31.0 e/nm³。图7(e)和图7(f)所示为同时包含空位、A位置和B位置的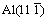面，无应力状态下，空位周围6个铝原子间的电子密度是相同的，应力状态下，[011]方向A位置的铝原子两侧的电子密度相同，而[101]方向B位置的铝原子两侧的电子密度则不同。

应力对空位周围铝原子距离的影响如图8所示，应力状态下，完全弛豫的[011]方向的A位置铝原子与空位的距离减小，但其与空位周围其他位置(B，C)的铝原子的距离都增大，产生图(f)中的A两侧电子密度的对称性。[101]方向的B位置铝原子与空位的距离增大，与A位置铝原子的距离增大，但与C位置铝原子的距离减小，这种原子距离的不同造成了图7(f)中的电子密度的非对称性。空位与A和B位置铝原子的距离即扩散过程中的跃迁势垒，应力对不同方向跃迁势垒的影响导致了不同方向上自扩散激活能的区别。

3  讨论

应力与原子的扩散激活能的关系与空位与近邻原子、近邻原子之间的距离有着密切关系，从20世纪60年代以来，相关学者就这个问题进行了研究，其中最为著名的是Flynn的原子迁移力学理论^[19]，该理论使用弹性常数和应力下的跃迁距离、扩散势垒作为输入变量，将应力与扩散的关系表示出来。当时原子迁移力学理论只是考虑应力对原子间距的影响，并没能考虑应力下的原子弛豫。在计算机迅速发展的今天，使用第一性原理手段进行应力下的原子弛豫已经很容易，所以将原子弛豫后的跃迁距离和扩散势垒作为原子迁移动力学理论的输入参数进行计算，会在一定程度上使结果精确。使用NEB过渡态搜索的方法计算扩散激活能不需要迁移动力学理论模型中所需要的力学常数等实验数据，完全从第一性原理出发，结果会更准确。

图7  含空位晶体在不同面的电子密度

Fig. 7  Electron density of defect crystal in different crystal planes

图8  缺陷体系应力下空位与近邻铝原子距离变化示意图

Fig. 8  Schematic of change in distance between vacancy and the nearest neighbors of defect system under stress

3.1  原子迁移动力学理论模型(Flynn’s model)

当对一立方晶体施加外加单向拉伸应力(σ₁=σ)时，立方晶体将会沿外力方向发生一个十分微小的弹性变形，原子间的相对距离发生变化，使得跃迁距离l(空位与其近邻原子的距离)和势垒距离y(空位周围的次近邻原子距离)发生变化，这会对扩散过程产生影响。根据Flynn的原子迁移动力学理论，原子扩散激活能Q与弹性常数C和弹性应变γ之间的关系可以表示为：

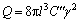                (8)

根据误差理论，可以将上述表达式中各个参数之间的变化关系表示为：

              (9)

将△γ/γ转换成-△y/y，故式(9)可表示为：

             (10)

利用弹性力学和几何关系，并且忽略二阶小项ε²，可以得到：

，

          (11)

式中：；。

扩散激活能的变化与跃迁距离l和势垒距离y有关，而这两者在[100]方向的外力作用下分别有2个不同的值，为l_[011]，l_[101]，y_[011]和y_[011]，由式(10)可以分别计算两者的变化得到激活能的变化。

3.2  考虑原子弛豫的Flynn模型

之前有学者利用Flynn理论进行研究时，是利用弹性常数计算得到不同应变下的跃迁距离和势垒距离的变化，从而计算出不同应变和应力下的扩散激活能，并没有考虑空位周围原子的弛豫。针对这一问题，本文讨论了弛豫对跃迁距离和势垒距离的影响，并利用第一原理弛豫之后的原子位置得到跃迁距离和势垒距离，在Flynn理论的基础上计算了不同方向上扩散激活能的比值。

为了得到弛豫对跃迁距离l和势垒距离y的影响，作未弛豫和弛豫后的l和y随外力的变化关系图，如图9所示。从图9可以看出：弛豫对l和y的数值以及随应力的变化斜率都有影响。未弛豫的原子随着应力的增大，在[011]方向的跃迁距离增大，势垒距离减小，在[101]方向的跃迁距离减小，势垒距离增大。弛豫的结果中[011]和[101]2个方向上的势垒距离都逐渐增大，但跃迁距离l则体现出不同的特征：[011]扩散方向上的跃迁距离减小，[101]扩散方向上的跃迁距离增大。由式(10)可知：势垒距离y随应力变化的斜率和跃迁距离l随应力变化的斜率共同影响着自扩散激活能的变化。

图10所示为外力作用下与无外力下自扩散激活能的比值在不同扩散方向上的随应力的变化。从图中可以看出，自扩散激活能在[011]方向上随应力的增大而减小，在[101]方向上随应力的增大而增大。在相同的应力条件下，应力对[011]方向自扩散激活能的影响要小于对[101]方向自扩散激活能的影响。对比Flynn模型和考虑原子弛豫的Flynn模型可以看出：原子弛豫使应力对扩散行为的影响减小，这点在[011]扩散方向上尤为明显。

3.3  第一性原理与原子迁移动力学结果比较

通过不同方法计算得到的自扩散激活能在不同扩散方向上均体现出了差异性，使用自扩散激活能在[011]扩散方向和[101]扩散方向上的比值表征扩散的各向异性，如图11所示。由图11可见：随着应力的增大，2个方向自扩散激活能的比值增大，不同方法计算的比值有不同。在同一应力下，Flynn的模型计算的比值最小，2个方向自扩散激活能差距最大；考虑原子弛豫的Flynn模型计算的结果次之；使用第一性原理NEB过渡态搜索方法计算的比值最大，自扩散激活能的差异性最小。

图9  弛豫和未弛豫下跃迁距离l和势垒距离y随外力的变化

Fig. 9  Jump distance l and barrier distance y with and without relaxation as function of stress

图10  外力与无外力作用下自扩散激活能的比值随应力的变化

Fig. 10  Ratio of activation energies with and without stress as function of stress

从分析的结果可以看出：Flynn模型过大的体现了应力对扩散行为的影响，6%应变下Q_[011]/Q_[101]达到0.72，这除了没有考虑原子弛豫和使用试验参数外，只使用二维模型计算也是主要原因。第一性原理的结果下应力对扩散行为的影响相对减小，6%应变下Q_[011]/Q_[101]为0.90，并且随着应力的增大，应力对Q_[011]/Q_[101]的影响逐渐减小。

图11  [011]和[101]2个方向上自扩散激活能的比值随着应力的变化

Fig. 11  Ratio of activation energies in [011] and [101] directions as function of stress

4  结论

(1) [100]方向的单轴拉伸应力增大了铝的空位形成能。无应力时铝的空位形成能为0.695 eV，在6%的应变下铝的空位形成能增大为0.826 eV。

(2) 在[100]方向的单轴拉伸应力作用下，铝的自扩散激活能在[011]扩散方向上减小，在[101]扩散方向上增大，应力导致了铝原子自扩散的各向异性。无应力作用下铝的自扩散激活能为1.303 eV，6%的应变下[011]方向的自扩散激活能为1.234 eV，[101]方向的自扩散激活能为1.371 eV。

(3) 不同计算方法得到的[011]扩散方向与[101]扩散方向的比值随应力变化程度不同。未考虑原子弛豫的Flynn模型计算得到的比值随应力变化程度最大，考虑原子弛豫的Flynn模型次之，第一性原理过度态搜索方法得到的结果最小。

参考文献：

[1] Zhu A W, Starke E A. Stress aging of Al-xCu alloys: Experiments[J]. Acta Materialia, 2001, 49: 2285-2295.

[2] 陈大钦, 郑子樵, 李世晨, 等. 外加应力对Al-Cu及Al-Cu-Mg-Ag合金析出相生长的影响[J]. 金属学报, 2004, 40(8): 799-804.

CHEN Daqin, ZHENG Ziqiao, LI Shichen, et al. Effect of external stress on the growth of precipitate in Al-Cu and Al-Cu-Mg-Ag alloys[J]. Acta Metallurgica Sinica, 2004, 40(8): 799-804.

[3] 陈大钦, 李世晨, 郑子樵, 等. 共格沉淀析出过程的模拟. Ⅱ: 外加应力场的影响[J].中国有色金属学报, 2006, 16(1): 116-122.

CHEN Daqin, LI Shichen, ZHENG Ziqiao, et al. Simulations of precipitation process of coherent particles. Ⅱ: Effect of external stress[J]. The Chinese Journal of Nonferrous Metals, 2006, 16(1): 116-122.

[4] 王宏伟, 易丹青, 蔡金伶, 等. 应力时效对2E12 铝合金的力学性能和微观组织的影响[J]. 中国有色金属学报, 2011, 21(12): 3019-3025.

WANG Hongwei, YI Danqing, CAI Jinling, et al. Effect of stress aging on mechanical properties and microstructures of 2E12 aluminum alloy[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(12): 3019-3025.

[5] 曹素芳, 潘清林, 刘晓艳, 等. 外加应力对Al-Cu-Mg-Ag合金时效析出行为的影响[J]. 中国有色金属学报, 2010, 20(8): 1513-1519.

CAO Sufang, PAN Qinglin, LIU Xiaoyan, et al. Effects of external stress on aging precipitation behavior of Al-Cu-Mg-Ag alloy[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(8): 1513-1519.

[6] Ardell A J, Prikhodko S V. Coarsening of γ′ in Ni-Al alloys aged under uniaxial compression: II. Diffusion under stress and retardation of coarsening kinetics[J]. Acta Materialia, 2003, 51(17): 5013-5019.

[7] Chen Z Z, Kioussis N, Ghoniem N, et al. Strain-field effects on the formation and migration energies of self interstitials in α-Fe from first principles[J]. Physical Review B, 2010, 81(9): 094102.

[8] Yashiro K, Oho M, Tomita Y. Ab initio study on the lattice instability of silicon and aluminum under [001] tension[J]. Computational Materials Science, 2004, 29(4): 397-406.

[9] WANG Yunjiang, WANG Chongyu. Influence of the alloying element Re on the ideal tensile and shear strength of γ′-Ni₃Al[J]. Scripta Materialia, 2009, 61(2): 197-200.

[10] Ceperley D M, Alder B J. Ground state of the electron gas by a stochastic method[J]. Physical Review Letters, 1980, 45(7): 566-569.

[11] Kresse G, Furthmuller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set[J]. Physical Review B, 1996, 54(16): 11169-11186.

[12] Mills G, Jonsson H. Quantum and thermal effects in H₂ dissociative adsorption: Evaluation of free energy barriers in multidimensional quantum systems[J]. Physical Review Letters, 1994, 72(7): 1124-1127.

[13] Wang C, Han P D, Zhang L, et al. The strengthening effect of Al atoms into Mg-Al alloy: A first-principles study[J]. Journal of Alloys and Compounds, 2009, 482(1/2): 540-543.

[14] Lu G H, Deng S H, Wang T M. Theoretical tensile strength of an Al grain boundary[J]. Physical Review B, 2004, 69(13): 134106.

[15] 师昌绪. 材料大词典[M] . 北京:化学工业出版社, 1994: 1060-1061.

SHI Changxu. Materials dictionary[M]. Beijing: Chemical Industry Press, 1994: 1060-1061.

[16] Carling K, Wahnstrom G. Vacancies in metals: from first-principles calculations to experimental data[J]. Physical Review Letters, 2000, 85(18): 3862-3865.

[17] Sandberg N, Magyari-kope B, Mattsson T R. Self-diffusion rates in Al from combined first-principles and model-potential calculations[J]. Physical Review Letters, 2002, 89(6): 065901.

[18] Mantina M, Wang Y, Arroyave R, et al. First-principles calculation of self-diffusion coefficients[J]. Physical Review Letters, 2008, 100(21): 215901.

[19] Flynn C P. Atomic migration in monatomic crystals[J]. Physical Review, 1968, 171(3): 682-698.

(编辑  杨幼平)

收稿日期：2012-06-04；修回日期：2012-10-21

基金项目：国家自然科学基金资助项目(51071177)

通信作者：易丹青(1954-)，男，湖南湘乡人，教授，博士生导师，从事高性能轻合金及粉末冶金新材料研究；电话：0731-88830263；E-mail：yioffice@ csu.edu.cn