
Simulation of texture evolution during plastic deformation of FCC, BCC and HCP structured crystals with crystal plasticity based finite element method
HUANG Shi-yao, ZHANG Shao-rui, LI Da-yong, PENG Ying-hong
State Key Laboratory of Mechanical System and Vibration, School of Mechanical and Power Energy Engineering, Shanghai Jiao Tong University, Shanghai 200240, China
Received 19 August 2010; accepted 16 December 2010
Abstract: Two alternative formulations of single crystal plasticity model were introduced respectively and two schemes were implemented in the explicit FE code with software ABAQUS/Explicit by writing the user subroutine VUMAT. Meshes containing material data were created with solid elements. Each element represented an individual grain, and the grain orientations were explicitly stored and updated at each increment. Tangential modulus method was employed to calculate the plastic shear strain increment of deformation systems in combination with a hardening law to describe the hardening responses. Both two developed subroutines were applied to simulate the texture evolution during the uniaxial tension of copper (FCC), cold rolling of IF steel (BCC) and uniaxial compression of AZ31 magnesium alloy (HCP). The predicted texture distributions are in qualitative agreement with the experimental results.
Key words: single crystal model; texture; additive decomposition; multiplicative decomposition
1 Introduction
Crystal plasticity has attracted a lot of interests due to its ability to set up relationships between material behavior and microstructure. Recently, with the significant increase in computational power, crystal plasticity based finite element method (CPFEM) has been widely applied to simulate forming process and predict texture evolution during deformation. The various applications of CPFEM can be classified into three major types: 1) each element represents an individual grain [1], 2) each element represents a set of grains [2], and 3) several elements describe an individual grain [3]. Compared with the last two methods, the first approach provides the most straightforward means to represent the polycrystalline aggregate. Since crystal plasticity model is not available as standard in the commercial FE software, this approach requires implementing single crystal model in FE software.
The single crystal plasticity models can be categorized into two major types: the rate independent model and the rate dependent model. Regardless of the type of crystal model, there are typically two different methods to formulate the single crystal model, additive decomposition of the velocity gradient L and multiplicative decomposition of the deformation gradient F. However, there has been few contrasting work between the two formulations, most previous research has concentrated on either formulation. Furthermore, systematic study on different crystal structures (FCC, BCC and HCP) with two formulations is seldom found.
In this study, two formulations of single crystal plasticity model were introduced, respectively. The rate dependent model is implemented in the commercial finite element software ABAQUS/Explicit by writing the user subroutine VUMAT. The integration schemes were applied to FCC, BCC and HCP crystals for model validation and comparison.
2 Two formulations of single crystal model
2.1 Additive decomposition of velocity gradient
The velocity gradient L is expressed as follows:
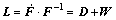 (1)
(1)
where F is the deformation gradient; D is the symmetric part of the deformation rate; and W is the skew symmetric spin tensor. D and W can be decomposed into elastic and plastic parts as:
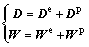 (2)
(2)
In increment n, 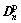 and
and 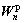 are related to the grain level plastic strain rate
are related to the grain level plastic strain rate 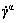 as:
as:
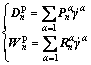 (3)
(3)
 and
and 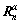 can be defined as:
can be defined as:
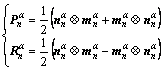 (4)
(4)
where the slip direction in the current configuration is designated by the unit vector mn and the slip plane normal in the current configuration by the unit vector nn, and the superscript α is the number of deformation systems. A rate dependent constitutive rule [4] is employed to relate the plastic shear strain rate  and the shear stress
and the shear stress 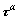 as:
as:
 (5)
(5)
where gα denotes the critical resolved shear stress (CRSS) to describe the current strain hardening state of the crystal; 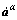 is the reference shear rate and m is the material rate sensitivity. The solution of
is the reference shear rate and m is the material rate sensitivity. The solution of  is making use of tangential modulus method [5-6]. Then the elastic constitutive equation can be specified as:
is making use of tangential modulus method [5-6]. Then the elastic constitutive equation can be specified as:
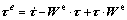 (6)
(6)
where 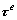 is the Jaumann rate of the Kirchhoff stress tensor τ based on the lattice rotations.
is the Jaumann rate of the Kirchhoff stress tensor τ based on the lattice rotations.
In each increment, the rigid body rotation matrix can be expressed as [7]:
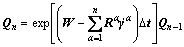 (7)
(7)
where Q defines the orientation of the crystal coordinate system with respect to the global coordinate system.
The CRSS gα is evolved according to the hardening law,
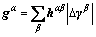 (8)
(8)
with
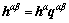 (9)
(9)
where hαβ is the hardening modulus and qαβ is introduced to describe the self and latent hardening. The following equation is employed to describe hα [8],
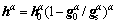 (10)
(10)
where 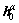 is the initial hardening rate;
is the initial hardening rate; 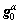 is the initial CRSS;
is the initial CRSS; 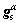 is the saturation value of deformation resistance and a is the hardening exponent.
is the saturation value of deformation resistance and a is the hardening exponent.
The flow chart of this calculation is shown in Fig. 1.

Fig. 1 Flow chart for additive decomposition of velocity gradient
2.2 Multiplicative decomposition of deformation gradient
The kinematics based on multiplicative decomposition of the deformation gradient is expressed as:
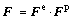 (11)
(11)
where Fp is the deformation solely due to plastic shearing along crystallographic slip systems, while the elastic deformation and any rigid body rotation are embodied in Fe. In addition, the elastic component Fe is decomposed into the symmetric left elastic stretch tensor Ve and the rotation tensor Re (det Re =1).
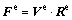 (12)
(12)
In increment n, the green strain En can be calculated as:
 (13)
(13)
Since 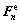 is unknown at the beginning of the increment,
is unknown at the beginning of the increment, 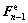 should be used from last increment as a trial input to calculate the trial green strain
should be used from last increment as a trial input to calculate the trial green strain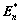 . Then the trial second Piola-Kirchhoff stress
. Then the trial second Piola-Kirchhoff stress  is calculated as
is calculated as
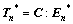 (14)
(14)
where C is the elasticity matrix. The trial resolved shear stress on each deformation system can be calculated as:
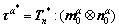 (15)
(15)
where the slip direction in the initial configuration is designated by the unit vector 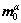 and the slip plane normal in the initial configuration is designated by the unit vector
and the slip plane normal in the initial configuration is designated by the unit vector 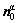 . Then the plastic deformation gradient is updated by the following equation:
. Then the plastic deformation gradient is updated by the following equation:
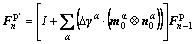 (16)
(16)
where 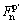 is normalized by
is normalized by
 (17)
(17)
With the normalized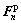 , the elastic component
, the elastic component 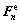 is calculated according to Eq. (11). Then the second Piola-Kirchhoff stress Tn is recalculated with the updated
is calculated according to Eq. (11). Then the second Piola-Kirchhoff stress Tn is recalculated with the updated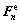 , the procedures are repeated until that the trial second Piola-Kirchhoff stress
, the procedures are repeated until that the trial second Piola-Kirchhoff stress 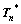 coincides with the recalculated
coincides with the recalculated 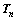 .
. 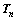 can be converted to Cauchy stress
can be converted to Cauchy stress 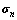 by
by
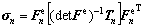 (18)
(18)
At the end of each increment, the rotation tensor Re can be calculated by Eq. (12). Then grain orientation is updated based on the following equation:
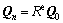 (19)
(19)
where Qn is the rotation tensor in the deformed configuration and Q0 is the rotation tensor in the initial configuration.
The evolution of CRSS is also calculated according to Eqs. (8)-(10). The calculation scheme for multiplicative decomposition of the deformation gradient is shown in Fig. 2.
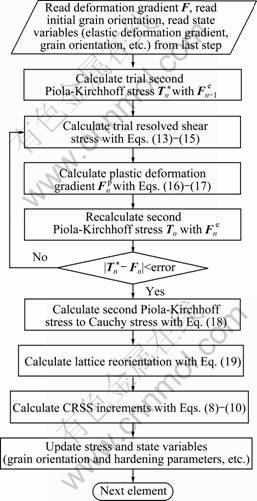
Fig. 2 Flow chart for multiplicative decomposition of deformation gradient
3 Modelling texture evolution during deformation
Crystal plasticity constitutive theory is not available as standard in the commercially FE software ABAQUS. However, ABAQUS provides an interface where ABAQUS/Explicit users can define the constitutive behavior of a material with the user subroutine VUMAT. ABAQUS/Explicit solution process involves large number of increments. Stress and state variables (orientation and hardening parameters of each individual grain) at each material point are passed in at the beginning of each increment and then updated at the end of increment. In this section, texture evolution during the deformation of FCC, BCC and HCP crystals were simulated with two developed subroutines. All the simulations were accelerated by adopting proper mass-scaling factor. To preclude the influence of material parameters, the same values of critical resolved shear stress (CRSS) and hardening parameters for two models were adopted.
3.1 FCC crystal
As the first example, two subroutines were applied to simulate the texture evolution during uniaxial tension of copper. The simulation results were compared with the experiment results [9]. The tension test was carried out at a strain rate of 0.001 s-1 to a strain level of 0.37. The initial texture is randomly distributed and the deformed texture is shown in Fig. 3.
A rectangular model was built to simulate the tension test. The geometry was meshed with 1000 elements, type C3D8R. Each element in the FE model was initialized with a random grain orientation. The random texture distribution of the polycrystalline aggregate is plotted in Fig. 4. The potential slip systems for FCC crystal were the 12 {111}á110? systems. The components of the elasticity tensor were: C11=170 GPa, C12=124 GPa and C44=75 GPa [9]. The plasticity parameters were chosen according to BRONKHORST et al [9]. The self hardening ratio was set to 1.0, while the latent hardening ratio was set to 1.4. Figures 5 and 6 show the texture distribution predicted by two formulations respectively. It can be seen that the two textures are virtually identical. In addition, the simulation results are close to the experiment result shown in Fig. 3.

Fig. 3 Experimental texture distribution of copper after uniaxial tension [8]
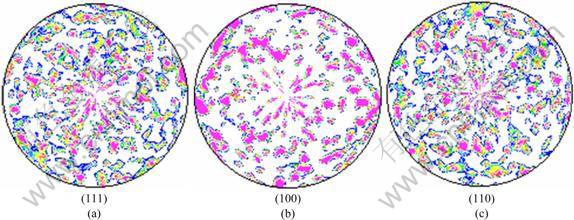
Fig. 4 Representation of random texture distribution of copper
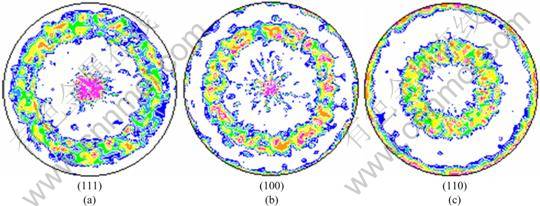
Fig. 5 Simulated texture of copper by additive decomposition of velocity gradient
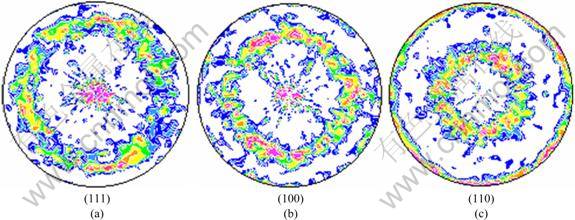
Fig. 6 Simulated texture of copper by multiplicative decomposition of deformation gradient
3.2 BCC crystal
For BCC crystal, texture evolution of IF steel during cold rolling was simulated. The predicted texture was compared with the published simulation result [10]. The simulation procedure studied by LI et al [10] is described as follows: cold rolling process is simulated by plain strain compression to a strain level of 1.39 with a nominal strain rate of -0.001 s-1. The initial texture distribution of IF steel is almost random, and the predicted (100) pole figure is shown in Fig. 7.

Fig. 7 (100) pole figure of IF steel predicted by LI et al [10]
Since cold rolling can be simulated by plane strain compression, a finite element model contains 1000 elements built to simulate the plane strain compression. The input texture was the same as the one shown in Fig. 4. The reference slip system families were 12{110}á111? and 12 {112}á111? systems. The values of the parameters in elastic tensor were: C11=230 GPa, C12=135 GPa and C44=117 GPa [10]. The values of the plasticity parameters were derived from another research on the ferritic low carbon steel [8]. The predicted (100) pole figures are displayed in Fig. 8. Two formulations present a similar texture pattern, which is also in qualitative agreement with the prediction by LI et al [10].
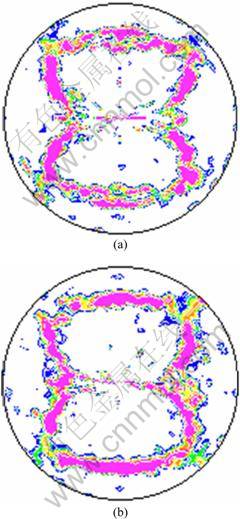
Fig. 8 Simulated (100) pole figure of IF steel after cold rolling: (a) Additive decomposition of L; (b) Multiplicative decomposition of F
3.3 HCP crystal
As the last example, two subroutines were applied to simulating the texture evolution during uniaxial compression of AZ31 magnesium alloy. To evaluate the accuracy of two formulations, uniaxial compression was carried out at room temperature to a strain level of -0.15 at a nominal strain rate of -0.01 s-1. The round specimen (with dimensions of d 10 mm×15 mm) was machined from extruded AZ31 rod. The compression direction was parallel to the extrusion direction (ED), and the texture distribution was measured by electron backscattered diffraction (EBSD). Figure 9 shows the texture distribution of original and deformed samples with the observed plane perpendicular to ED, suggesting that strong basal texture was formed during the compression test.
Twinning can be activated to compensate due to the lack of crystal symmetry in HCP crystal. The activity of twinning highly depends on temperature, alloying content, stacking fault energy and the specific crystal lattice structure [11]. In the case of AZ31 magnesium alloy, tensile twinning plays an important part in accommodating strain during the deformation, especially at low temperature [12]. The contribution of twinning to the grain reorientation is calculated by Predominant twin reorientation (PTR) scheme [13]. In this scheme, a threshold value for twinning reorientation (FT) can be defined by
 (20)
(20)
where VE is the effective twinned fraction; VR is the total volume fraction of accumulated twins, and a and b are constants. At every increment, if the accumulated twinned fraction of the most active twinning system exceeds the threshold value, the whole grain is reoriented following the predominant twinning system. Then this reoriented grain is added to the effective twinned fraction, VE. As more grains are reoriented by twinning, FT increases with the increment of VE. Further reorientation by twinning is inhibited until VR catches up.
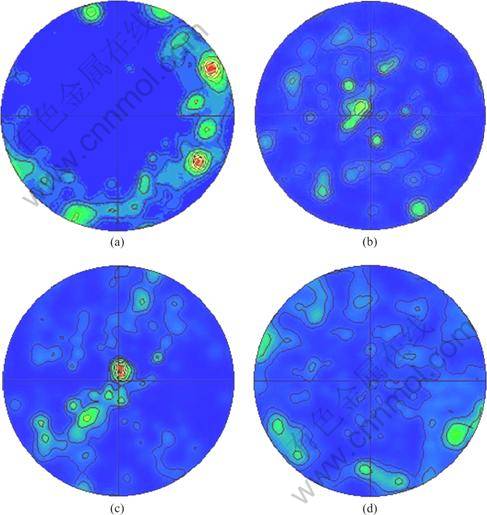
Fig. 9 Texture distributions of initial and deformed AZ31 magnesium alloy: (a) Initial (0001); (b) Initial  ; (c) Deformed (0001); (d) Deformed
; (c) Deformed (0001); (d) Deformed 
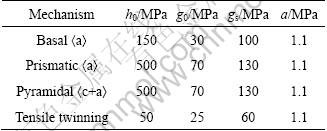
In addition to tensile twinning, three kinds of slip systems were assumed to be activated during deformation: basal áa?, prismatic áa? and pyramidal ác+a? slip systems [14-16]. In the current study, the values of CRSS and hardening parameters (Table 1) were derived from a previous research [16], where the same hardening law was employed. The values of the parameters in elastic moduli were: C11=58 GPa, C12=25 GPa, C13=20.8 GPa, C33=61.2 GPa and C55=16.6 GPa [14]. The latent hardening ratio for slip systems was set to 1.4, while it was set to 4.0 for twinning system to represent that the dislocation movement is inhibited by twinning boundary.
Table 1 Plasticity parameters for AZ31 alloy [16]
A cylindrical model with 1707 elements was built to simulate compression test. The input texture was the ideal (0001) fiber texture, as shown in Fig. 10. Figure 11 presents the predicted (0001) pole figures. With the same input texture and parameter values, both two integration schemes predicted the formation of basal texture during compression. But compared with experimental result in Fig. 9, two integration schemes predicted more scattered basal texture. In addition, the deviation between Figs. 11 (a) and (b) can not be neglected.
The values of CRSS and the hardening parameters of different slip and twinning systems in AZ31 alloy have been widely reported [14-17] in the recent years, the differences between these values are distinct. The values of CRSS and hardening parameters are generally obtained by an inverse parameter calculation, namely fitting the experimental stress—strain curves. Thus, they are appropriate for interpreting the phenomenological results rather than representing material constants. Note that CRSS and hardening parameters are derived from a previous research [16], which may not be precise for the current integration schemes. A stronger basal texture can be predicted by either integration scheme if the values of CRSS and hardening parameters are properly adjusted.
It shows that both two formulations are appropriate for FCC, BCC and HCP structured crystals. Nevertheless, the multiplicative decomposition of F involves iteration until a convergence criterion is satisfied for each increment, while the additive decomposition of L is solved directly to determine the solution at the end of the increment without iteration. Thus, the additive decomposition of L has the advantage of computational efficiency although the two algorithms present a similar simulation result. In the last example of uniaxial compression of AZ31 Mg alloy, it takes about 1.5 h for the formulation of multiplicative decomposition of F, while the simulation can be finished in 35 min with the formulation of additive decomposition of L.
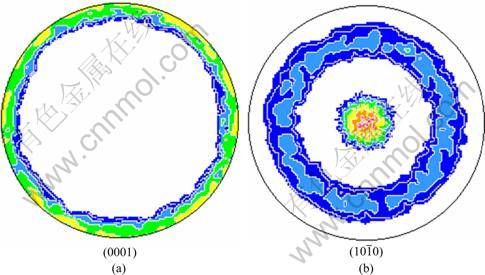
Fig. 10 Initial texture distribution simulation of AZ31 magnesium alloy
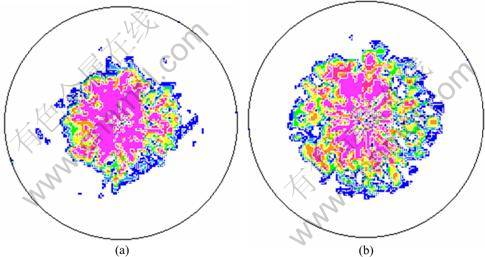
Fig. 11 Simulated (0001) pole figure after uniaxial compression of AZ31 Mg alloy: (a) Additive decomposition of L; (b) Multiplicative decomposition of F
4 Conclusions
1) The prediction shows qualitative agreement with the experimental results. The additive decomposition of L has the advantage of computational efficiency although two algorithms present a similar simulation result.
2) Two formulations predict similar result for FCC and BCC crystals. The deviation of prediction in AZ31 alloy suggests that the precise material parameters are important for texture prediction in HCP crystal with low symmetry.
References
[1] ZHANG Shao-rui, LI Da-yong, PENG Ying-hong, LIANG Sheng. FCC sheet earring based on rate-independent polycrystalline plasticity FEM [J]. Material Science & Technology, 2004, 12(4): 372-374. (in Chinese)
[2] ZHAN Shao-rui, LI Da-yong, PENG Ying-hong, LIANG sheng, LIU Shou-rong, QIU Su-ping. Finite element simulation of sheet metal stamping with polycrystalline plasticity [J]. Chinese Journal of Mechanical Engineering, 2008, 44: 190-194. (in Chinese)
[3] Prakash A, Weygand S M, Riedel H. Modeling the evolution of texture and grain shape in Mg alloy AZ31 using the crystal plasticity finite element method [J]. Computational Materials Science, 2009, 45(3): 744-750.
[4] Hutchinson J W. Bounds and self-consistent estimates for creep of polycrystalline materials [J]. Proceedings of the Royal Society of London A, 1976, 348: 101-127.
[5] Peirce D, Asaro R J, Needleman A. An analysis of nonuniform and localized deformation in ductile single crystals [J]. Acta Metallurgica, 1982, 30(6): 1087-1119.
[6] Peirce D, Asaro R J, Needleman A. Material rate dependence and localized deformation in crystalline solids [J]. Acta Metallurgica, 1983, 31(12): 1951-1976.
[7] Simo J C, Vu-Quoc L. A three-dimensional finite-strain rod model. Part II: Computational aspects [J]. Computer Methods in Applied Mechanics and Engineering, 1986, 58(1): 79-116.
[8] Raabe D, Wang Y, Roters F. Crystal plasticity simulation study on the influence of texture on earing in steel [J]. Computational Materials Science, 2005, 34(3): 221-234.
[9] Bronkhorst C A, Kalidindi S R, Anand L. Polycrystalline plasticity and the evolution of crystallographic texture in FCC metals [J]. Philosophical Transactions: Physical Sciences and Engineering, 1992, 341: 443-477.
[10] Li H, Han J, Pi H, Jiang Z, Wei D, Kiet Tieu A. Modeling texture development during cold rolling of IF steel by crystal plasticity finite element method [J]. Journal of University of Science and Technology Beijing: Mineral, Metallurgy, Material, 2008, 15(6): 696-701.
[11] Prantil V, Jenkins J, Dawson P. Modelling deformation induced textures in titanium using analytical solutions for constrained single crystal response [J]. Journal of the Mechanics and Physics of Solids, 1995, 43(8): 1283-1302.
[12] Wang Y N, Huang C C. The role of twinning and untwinning in yielding behavior in hot-extruded Mg-Al-Zn alloy [J]. Acta Materialia, 2007, 55(3): 897-905.
[13] Tomé C N, Lebensohn R A, Kocks U F. A model for texture development dominated by deformation twinning: Application to zirconium alloys [J]. Acta Metallurgica et Materialia, 1991, 39(11): 2667-2680.
[14] Staroselsky A, Anand L. A constitutive model for hcp materials deforming by slip and twinning: application to magnesium alloy AZ31B [J]. International Journal of Plasticity, 2003, 19(10): 1843-1864.
[15] Agnew S R, Tomé C N, Brown D W, Holden T M, Vogel S C. Study of slip mechanisms in a magnesium alloy by neutron diffraction and modeling [J]. Scripta Materialia, 2003, 48(8): 1003-1008.
[16] Choi S H, Shin E J, Seong B S. Simulation of deformation twins and deformation texture in an AZ31 Mg alloy under uniaxial compression [J]. Acta Materialia, 2007, 55(12): 4181-4192.
[17] Jain A, Agnew S. Modeling the temperature dependent effect of twinning on the behavior of magnesium alloy AZ31B sheet [J]. Materials Science and Engineering A, 2007, 462(1-2): 29-36.
基于耦合有限元的晶体塑性力学模型的
FCC,BCC和HCP晶体织构演化的模拟
黄诗尧, 张少睿, 李大永, 彭颖红
上海交通大学 机械与动力工程学院,机械系统与振动国家重点实验室,上海 200240
摘 要:介绍单晶体模型的2种实现方法,并通过对有限元软件ABAQUS/Explicit的用户材料接口VUMAT做二次开发,实现2种单晶体模型构架和显式有限元方法的耦合。采取实体单元来存储材料信息,每个单元代表一个晶粒,在每个增量步中读取并更新晶粒取向。采用切线系数法来计算每个增量步中不同变形系统的塑性应变增量,通过硬化模型来描述硬化响应。利用编制的2种用户子程序模拟铜(FCC)单向拉伸过程、IF铁(BCC)冷轧过程和AZ31镁合金(HCP)单向压缩过程中的织构演化,模拟结果和试验结果吻合较好。
关键词:单晶体模型;织构;加法分解;乘法分解
(Edited by FANG Jing-hua)
Foundation item: Projects (50821003, 50405014) supported by the National Natural Science Foundation of China; Projects (10QH1401400, 10520705000, 10JC1407300) supported by Shanghai Committee of Science and Technology, China; Project (NCET-07-0545) supported by Program for New Century Excellent Talents in University, China; Project supported by Ford University Research Program
Corresponding author: LI Da-yong; Tel/Fax: +86-21-34206313; E-mail: dyli@sjtu.edu.cn
DOI: 10.1016/S1003-6326(11)60936-9