DOI： 10.11817/j.issn.1672-7207.2019.10.012
新型自协作移动机器人及其力学协调分配方法
张程煜,郭盛,赵福群
（北京交通大学 机械与电子控制工程学院，北京，100044）
摘要:为获取机器人在操作过程中的最优力学性能，以可以实现多种操作模式的新型轮腿复合机器人为研究对象，提出一种自协作模式下的机器人动力学计算方法。首先，运用牛顿-欧拉方法求解支链的动力学方程，得到支链与平台之间的作用力关系；然后，根据力可操作度指标与动平台承受载荷方向的关系，并以各支撑支链关节力矩最小为目标，提出机器人在自协作模式下支链位置以及支撑力的最优协调分配方法；最后，以特定操作任务为算例，对提出的计算方法进行实例计算与仿真验证。研究结果表明：在引入姿态调整环节后，机器人力矩范数与能耗明显降低，且理论计算结果与仿真结果呈现一致性。
关键词:轮腿复合机器人；自协作模式；动力学
中图分类号:TH112 文献标志码:A 开放科学(资源服务)标识码(OSID)
文章编号:1672-7207（2019）10-2435-11
New self-cooperation mobile robot and force coordinated distribution method
ZHANG Chengyu, GUO Sheng, ZHAO Fuqun
(School of Mechanical, Electronic and Control Engineering, Beijing Jiaotong University, Beijing 100044, China)
Abstract: In order to obtain the optimal mechanical performance of the robot during operation, a new wheel-legged robot that can realize multiple operating modes was taken as the research object, and a robot dynamics calculation method in self-cooperation mode was proposed. Firstly, the Newton-Eulerian method was used to solve the dynamic equation of the branch, and the force relationship between the branch and the platform was obtained. Then, with consideration of the relationship between the manipulability index and the load direction of the moving platform, taking the minimum joint torque of each support branch as the object, the optimal coordination and distribution method of the branch position and support force of the robot in self-cooperation mode were proposed. Finally, the calculation and the simulation of the calculation method proposed were carried out by taking the specific operation task as an example. The results show that after orientation adjustment, the robot torque norm and energy consumption are significantly reduced, and the theoretical calculation and simulation results are consistent.
Key words: wheel-legged robot; self-cooperation mode; dynamics
具有操作能力的移动机器人能够在移动模式与操作模式间切换，不仅具备优异的移动能力，而且能够通过模式切换完成不同类型的操作任务，更好地适应不同地形与复杂环境，成为移动机器人领域的一个发展新方向，也吸引越来越多学者的关注。国内外许多学者与研究机构提出了多种轮腿式机器人机构，如：丁希仑等[1-2]等提出了多种轮腿式机器人方案，并研究其运动学及构态变形方式；徐坤等[3]提出了一种圆周对称的六轮腿式机器人，并研究其步行模式与轮行模式下的步态。但目前已经研制出的轮腿式复合机器人大多数仅具备移动能力，不具备通过机器人自协作完成复杂操作任务的能力。为解决移动机器人操作能力不足的问题，ARAI等[4-5]与DING等[6-7]先后提出了具移动和操作能力多支链机器人的概念，前者对该类机器人的设计思路与应用领域进行了详细介绍，后者运用NOROS-III六足机器人，利用实验研究其腿部支链进行操作的控制方法，证明了腿部支链与手部支链切换操作与控制实现的可行性。动力学分析是机器人设计与实现中的重要环节，建立精确完整的机器人动力学模型是机器人仿真、实现机器人的控制策略、分析机器人力学性能表现的重要保证。ROY等[8-9]对六足步行机器人进行动力学建模，并基于最小二乘法给出了在步行移动过程中的支链载荷分配的最优解。董伟光等[10]运用牛顿-欧拉方法对一种具有闭链结构的轮足复合式机器人进行了动力学分析与试验，给出了机器人姿态对力学特征的影响。SHAH等[11]提出了一种模块化的足式机器人动力学建模方法，将整体划分为多个含有串联支链的模块，对于仅含有串联支链足式机器人动力学建模具有普适性。KOMODA等[12]对多种闭环支链构型的足式机器人进行了建模分析，并对比动力学性能与能量消耗，揭示了机器人设计与性能评价间存在一定联系。DING等[13]利用拉格朗日方法建立动力学模型，揭示了轮腿式机器人腿部关节力矩与机器人平台高度之间的关系。KOMSUOGLU等[14]用实验方法进一步证明了不同机器人步态与能耗之间的关系。GRAND等[15]以轮腿式机器人稳定性和牵引力为目标，提出了一种适应于非平坦地形的机器人位姿控制方法。郑建华等[16]以四足机器人为研究对象，对引入的弹簧腿进行动力学优化，抑制了行走过程中足底打滑等问题，显著提高了机器人的稳定性。DING等[17]研究了足式机器人足端与地形的接触力学问题，给出不同接触情况下的力学模型并进行了相应的实验验证。在移动操作机器人方面，张硕生等[18]运用牛顿-欧拉方法揭示了轮式移动平台与机械手之间的耦合作用力。董超等[19]对一种铰接式的车辆进行了运动学与动力学分析，为轮腿式机器人轮式行走模式下的动力学建模提供一定的理论依据。针对并联足式机器人，王洪波等[20]解决了四足并联机器人行走过程中的动力学耦合问题。XIN等[21]利用摩尔-彭若斯广义逆矩阵，在关节空间内求解了六足并联机器人的重载条件下的支链力分配问题，使得求解过程更高效。综上所述，人们对腿式机器人的动力学分析取得了一定进展，并致力于研究机器人足式支链的力学分配与搭载于移动平台的操作手动力学问题，但是，基于性能优化的轮腿式机器人操作模式下的动力学问题研究尚显不足。为此，本文作者针对提出的具有多种操作模式的新型轮腿复合式机器人，利用牛顿-欧拉法建立了机器人自协作模式下的完整动力学模型，并依据可操作度椭球理论，提出一种操作模式下支撑支链的位姿调整方案，以便有效地提高操作过程中的力学性能。
1 机构设计与运动学分析
1.1 构型描述与模式介绍
图1所示为本文提出的一种新型多操作模式轮腿复合机器人。由图1可见：机器人由6条支链与动平台构成，每条支链布置有3个转动关节与1个具有动力的主动轮，每个转动关节均为驱动关节；6条支链呈对称布置，动平台为正六边形结构。
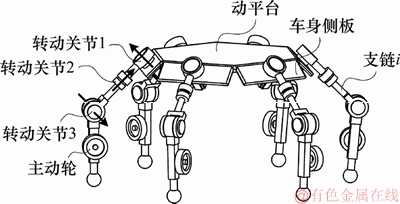
图1 轮腿复合机器人模型简图
Fig. 1 Schematic description of wheel-legged compound robot
支链可以作为腿部支撑支链，也可以作为手臂操作支链，并且每条支链上搭载驱动轮，从而通过支链的切换，机器人同时具备2类模式，即自协作模式与轮式移动模式，如图2所示。
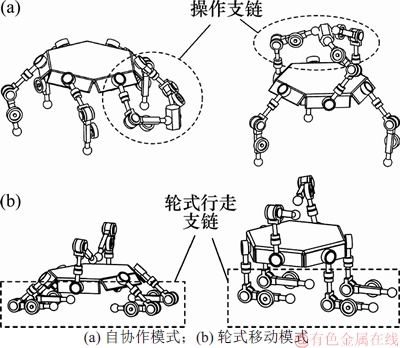
图2 机器人工作模式
Fig. 2 Robot wheeled modes
1.2 运动学分析
图3所示为机器人坐标系与支链分布示意图。图3(a)中，基坐标系为Oxyz，车身平台坐标系为Opxpypzp，其中坐标原点Op点与动平台的中心重合，zp轴垂直于动平台向上，xp指向六边形某一边的重点。车身平台为边长为2a的正六边形结构，车身侧板宽度为b。机器人具有6条完全相同且对称布置的支链，支链编号如图3(b)所示。
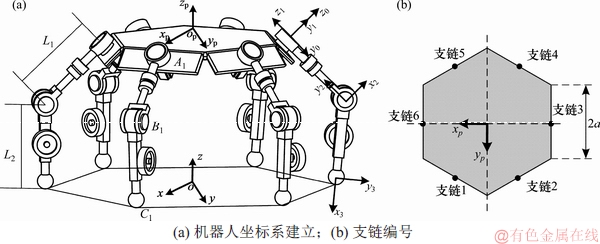
图3 机器人坐标系与支链分布示意图
Fig. 3 Schematic diagram of robot coordinate system and branch distribution
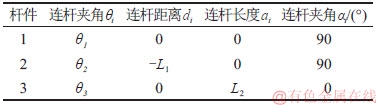
对于第i条支链(i=1,2,…,6)，其可以看作三自由度串联机械臂，支链连杆的长度分别为L1和L2，建立如图3(a)所示D-H坐标系，各个驱动关节的角度为θi(i=1,2,3)。当车身侧板角度为90°或135°时，其连杆坐标变换形式相同，因此，具有相同的D-H参数，如表1所示。
表1 串联支链D-H参数表
Table 1 D-H parameter table of series branch
支链在O0x0y0z0坐标系下的位姿变换矩阵可以表示为
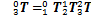
当车身侧板为90°时，第i条支链O0x0y0z0坐标系原点在Opxpypzp坐标系的位置可以表示为
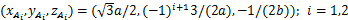
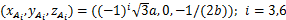
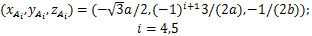
第i条支链支链在Opxpypzp坐标系下的位姿为
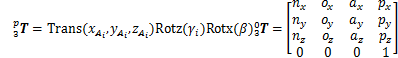
不同支链的对应γi角如表2所示。
表2 不同支链的γi角度
Table 2 γi angle values of different branches
利用上述方法计算得到机器人的雅克比矩阵维数为(6×3)，但是其中3行是线性无关的，值得考虑的是雅克比矩阵上方的(3×3)阶子矩阵：
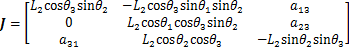
式中：
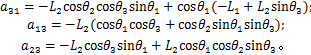
2 动力学建模
2.1 支链动力学模型
建立机器人单个串联支链的动力学模型如图4所示。支链细分为3个连杆，其中各连杆长度分别为L1，L2和L3，连杆质量分别为m1，m2和m3，车轮视为连杆3的一部分；连杆i的惯性张量在坐标系i下表示为iIi。
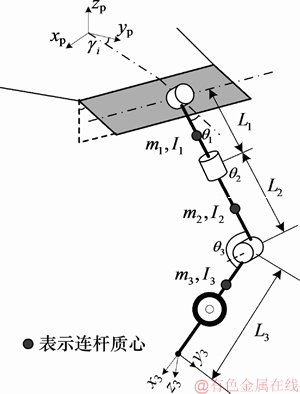
图4 串联支链动力学模型
Fig. 4 Dynamic model of series branch
给定平台的初始角速度和角加速度分别为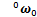
和
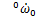，支链末端所受环境作用力与作用力矩分别为
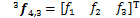与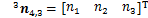
，根据牛顿-欧拉公式，连杆i与连杆i-1之间的作用力与作用力矩迭代关系式为
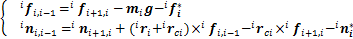(1)
式中：
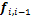和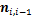
分别为i坐标系下第i条支链对i-1支链的作用力和作用力矩；
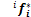为作用在连杆i质心的惯性作用力在i坐标系中的表示。利用旋转变换矩阵，可以实现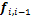和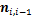在i坐标系与i-1坐标系下的转换：
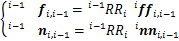(2)
根据连杆作用力在关节轴线上的投影关系，各关节力矩为
(3)
2.2 自协作模式动力学模型
在自协作模式下，通过支撑支链与操作支链的协同，机器人能够完成操作物体、自主维修等任务。将该模式下的动力学模型分为2个部分，即操作部分与支撑部分，如图5所示。为简化建模，进行如下假设：
1) 支链末端与地面接触时不存在滑动；
2) 支链末端与地面的接触为存在摩擦的点接触，即可以分解为1个垂直于地面和2个相切于地面的力分量。
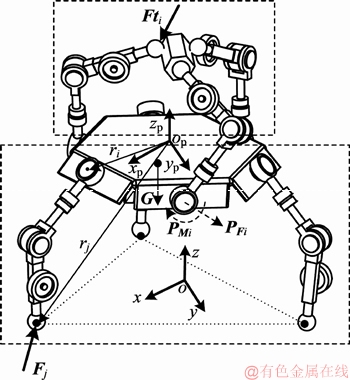
图5 自协作模式下机器人动力学模型
Fig. 5 Dynamic model of robot in self-cooperation mode
根据牛顿-欧拉法计算得到的单支链动力学方程，可以计算得到第i个操作支链中连杆1对动平台的作用力和作用力矩分别为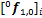
和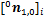
，将其转换到动平台质心处的基坐标系下，有
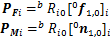(4)
机器人的6条支链中， m条支链为操作支链，n条支链为支撑支链，操作支链末端所受作用力为
，支撑支链末端所受作用力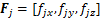
，PFi为第i个操作支链对动平台的作用力，G为动平台及操作支链所受重力，得到整体的力学平衡方程为
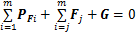(5)
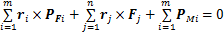(6)
将式(5)和式(6)整理成矩阵形式：
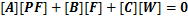(7)
其中：
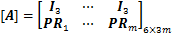
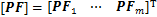
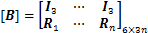
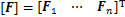
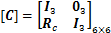
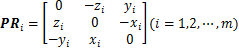
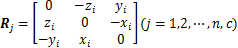
W为动平台质心处所受到的作用力与作用力矩，由于作用在刚体上的力矩不因矩心的变化而改变，因此，PMi可以等效为作用于动平台质心，从而W可以表示为
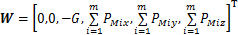
3 基于力学性能优化的调姿算法
力可操作性椭球体[22-23]可以应用于分析机构沿操作空间不同方向的力学可操作性。当给定某一任务方向时，可操作性椭球体在该方向的变换比率越大，则同等输出力的条件下所需关节力矩越小，从而在该方向的力学性能越好。
当动平台承受由操作支链加速度带来的作用反力与自身重力时，支撑支链的布置形式决定了式(7)中矩阵[A]，即决定了各支链的位姿，从而对支撑支链的力学表现性能有重要影响。在给定任务方向后，可以根据可操作度椭球在给定任务方向的变化比率，调整支撑支链的位姿，使得各支撑支链在任务方向上均达到最优力学性能。
考虑第j条支撑支链的力可操作度椭球如图6所示。
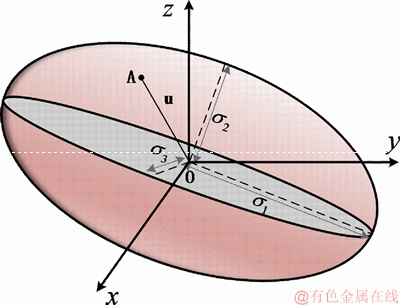
图6 力可操作度椭球
Fig. 6 Force manipulability ellipsoid
当操作部分支链的运动与外部作用力确定时，可以得到动平台质心所受作用力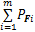
的方向。设该方向为u，在此方向上第j条支撑支链的力可操作度度量为|OA|，其可以表示为
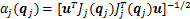
令每条支撑腿末端在满足期望的位置范围，如式(8)所示，并且在设置末端位置时应使得机器人重心落在支撑足各支撑点组成的多边形内。
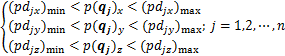(8)
各支撑支链在同一方向的力可操作度示意图如图7所示，在满足式(8)约束条件下，以支撑支链在u方向的力可操作度最大为目标，求解使得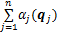
最大的关节变量qj。
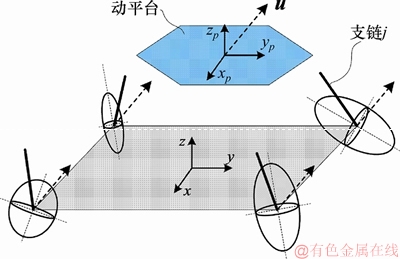
图7 支撑支链力可操作度示意图
Fig. 7 Schematic diagram of force manipulability of supporting branches
根据式(8)得到各关节变量qj，便可得到各支链位置与矩阵Rj，根据式(7)求解支撑支链的末端支撑力，当[F]具有最小范数解时，
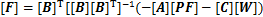(9)
从而第i条支撑支链的关节力矩为
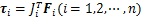(10)
经过优化得到的支链处于力学性能最佳位置，各关节力矩处于最小值，对于直流电机而言，静止条件下功率与力矩成正比，从而机器人的能耗也更低。
4 动力学计算结果
在自协作模式下，4条支链用于支撑，2条支链用于操作抓取物体，使物体产生一定的加速度，如图8所示。对比在引入调姿算法前后，各关节转矩的变化与机器人能耗的差异。
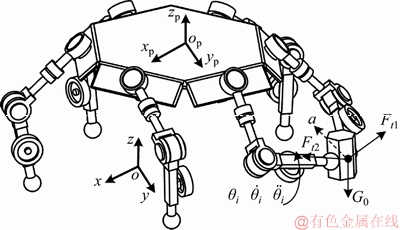
图8 操作过程示意图
Fig. 8 Schematic diagram of operating an object
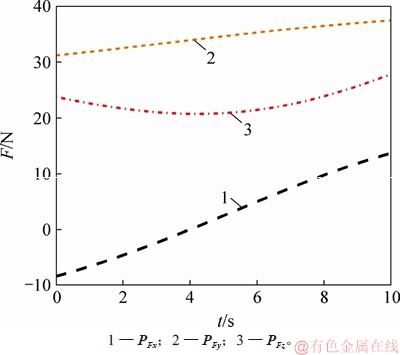
图9 动平台质心所受作用力
Fig. 9 Force of platform’s center of mass
机器人平台长a=200 mm，宽b=100 mm，连杆质量m1=m2=m3=1 kg，操作物体质量m0=1 kg，各连杆长度L1=200 mm，L2=200 mm，L3=400 mm，各连杆在自身坐标系下的惯性矩阵为：
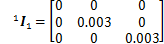
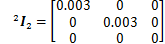
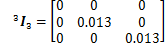
操作部分的力平衡方程为：
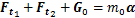
其中：Ft 1和Ft 2为2条操作支链对物体的作用力。令2条操作支链输出力相同，则有
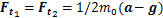
操作过程持续10 s，初始位置为(0.270,0.406,0.116)，目标位置(0.270,0.304,0.218)，被操作物体在x，y和z方向的加速度分别为-1.5，4.0和10.0 m/s2
4.1 未调姿状态下数值算例
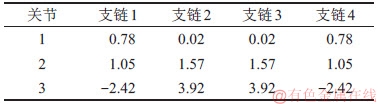
机器人通过四足或六足行走模式到达指定位置后，当不引入位姿调整环节时，支撑支链以行走过程中腿部支链的末状态位姿完成操作任务，此时，支撑支链的各关节角度如表3所示。
表3 未经调姿各关节角度
Table 3 Angle of each joint before orientation adjustmentrad
根据单支链动力学计算结果与式(1)，操作支链完成给定任务时，动平台质心所受到作用力变化如图9所示。
根据式(9)和式(10)可计算得到未调整姿态时各支链关节力矩与末端支撑力，其中，各支链关节力矩变化如图10所示。
4.2 调整姿态后数值算例
为获得在机器人操作过程中支撑支链的最优力学性能，在机器人到达指定位置后，引入姿态调整环节。根据动平台质心所受作用力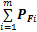
的方向，确定支撑支链的可操作度优化方向u。根据图10可知，在操作过程中的方向具有时变性，而u不随时间变化，所以，u要根据时变的力变化曲线确定差异最小的非时变方向，这里采用最小二乘法拟合得到方向u=[U1, U1, U3]，如图11所示。
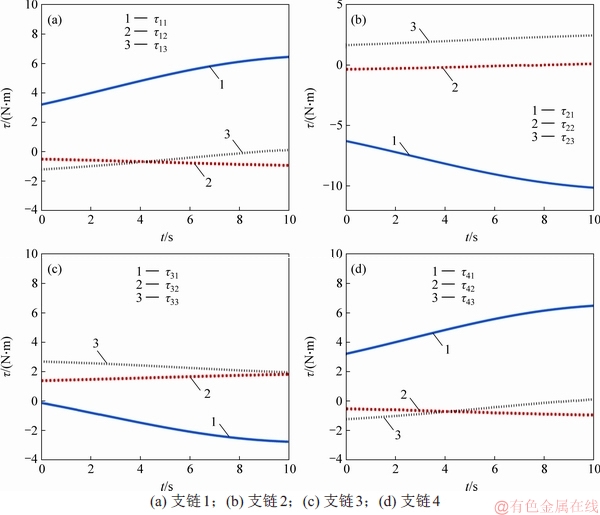
图10 未调整姿态时各支链关节力矩变化
Fig. 10 Joint torque variation of each branch before orientation adjustment
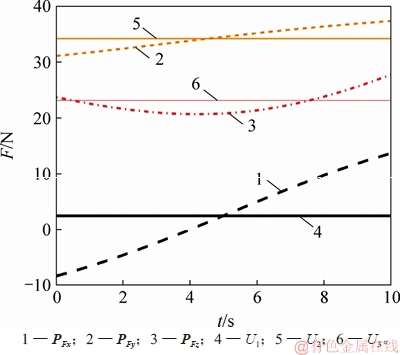
图11 动平台质心所受作用力与支撑方向选择
Fig. 11 Force of platform’s center of mass and support direction
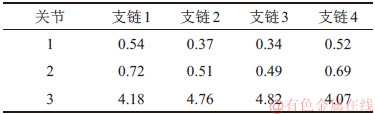
考虑机器人自身的几何约束并确保机器人重心落在支撑范围之内，确定各支撑支链末端位置的约束范围，如表4所示。
表4 支链末端位置约束范围
Table 4 Constraints of the end position of the branch mm
在满足表4所示的约束条件下，以u方向的可操作度最大为目标，对各支撑支链进行位姿调整，调整后的各支链关节角如表5所示。
表5 调姿之后各关节角
Table 5 Angle of each joint after orientation adjustmentrad
根据式(9)和式(10)可计算得到引入调整姿态环节后各支链关节力矩与末端支撑力。各支链关节力矩变化如图12所示，其中，τij表示第i条支链的第j个关节的关节力矩。
4.3 仿真验证与对比
在V-rep软件中对机器人操作过程进行仿真，验证调姿前后力矩范数与机器人能耗的变化。未引入调整姿态环节时机器人的操作过程如图13所示。引入调整姿态环节后机器人的操作过程如图14所示。
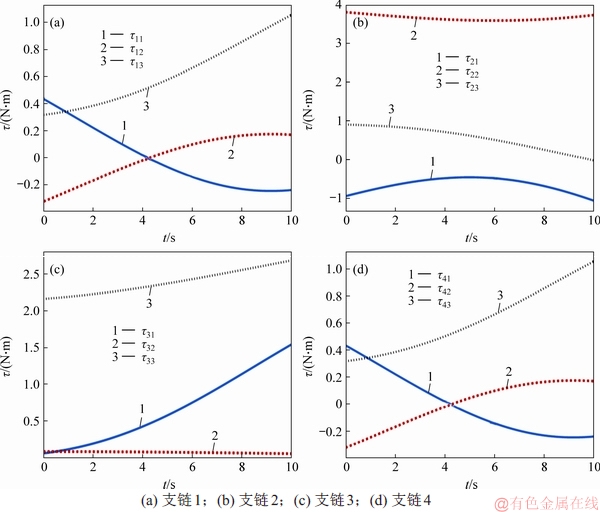
图12 调整姿态后各支链关节力矩变化
Fig. 12 Joint torque variation of each branch after orientation adjustment
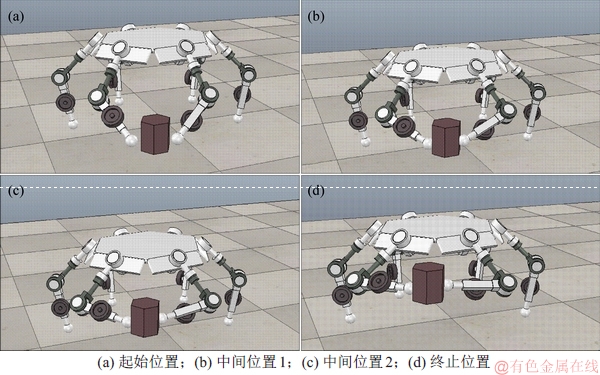
图13 未引入调整姿态环节操作过程
Fig. 13 Operation processes before orientation adjustment
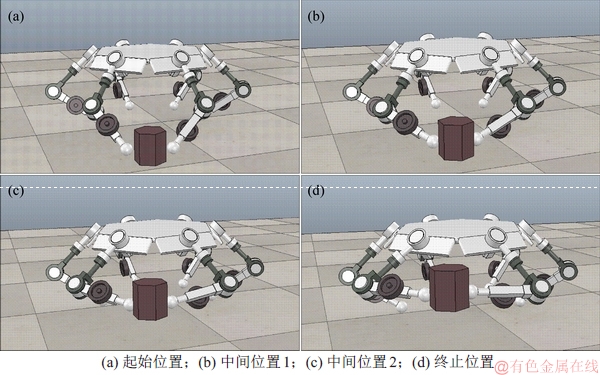
图14 引入调整姿态环节后操作过程
Fig. 14 Operation proceses after orientation adjustment
对调整位姿前后机器人关节力矩范数与能耗进行对比，结果如图15所示。由图15可见：在完成同样载荷任务的情况下，经过位姿调整环节后的关节力矩范数下降，机器人支撑部分的能耗降低63.8%。
5 结论
1) 基于提出的多操作模式轮腿复合机器人，利用牛顿-欧拉方法，将操作部分与支撑部分融合，建立了机器人自协作操作模式下的完整力学模型。
2) 考虑操作支链的动力学影响，以支撑支链的静力学可操作度椭球为目标，提出了一种支撑部分支链构型与支撑力分布的最优配置方法，能够使得机器人在最佳位姿完成操作任务。
3) 根据具体任务实例，计算操作过程中的各支链的力矩变化，并在V-rep中进行仿真实验。将力矩理论计算结果与仿真结果对比，结果证明了本文动力学模型建立的正确性与分析方法的有效性。
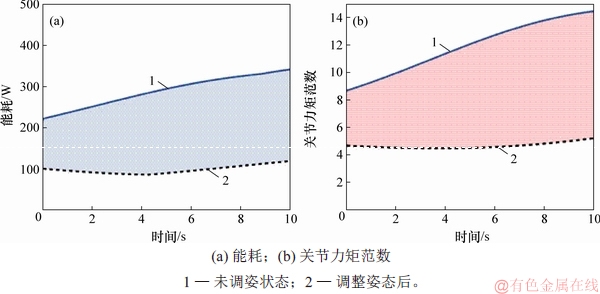
图15 支撑部分能耗与各关节力矩范数对比
Fig. 15 Energy consumption and torque norm comparison of support part
参考文献：
[1] 丁希仑, 徐坤. 一种新型变结构轮腿式机器人的设计与分析[J].中南大学学报(自然科学版), 2009, 40(S1): 91-101.
DING Xilun, XU Kun. Design and analysis of a novel metamorphic wheel-legged rover mechanism[J]. Journal of Central South University (Science and Technology) 2009, 40(S1):91-101.
[2] 王雁东, 唐昭, 戴建生. 连杆铰接轮腿式机器人的运动学与步态分析[J]. 机械工程学报, 2018, 54(7): 11-19.
WANG Yandong, TANG Zhao, DAI Jiansheng. Kinematics and Gait analysis of a linkage-jointed wheel-legged robot[J]. Journal of Mechanical Engineering, 2018, 54(7): 11-19
[3] 徐坤, 郑羿, 丁希仑. 六轮腿式机器人结构设计与运动模式分析[J]. 北京航空航天大学学报, 2016, 42(1): 59-71.
XU Kun, ZHENG Yi, DING Xilun. Structure design and motion mode analysis of a six wheel-legged robot[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(1): 59-71．
[4] ARAI T. Robots with integrated locomotion and manipulation and their future[J]. Journal of Robotics and Mechatronics, 1997, 9(4): 251-255.
[5] TAKAHASHI Y, ARAI T, MAE Y, et al. Development of multi-limb robot with omnidirectional manipulability and mobility[C]//International Conference on Intelligent Robots and Systems. New York, USA: IEEE, 2000: 2012－2017.
[6] DING Xilun, ZHENG Yi, XU Kun. Wheel-legged hexapod robots: a multifunctional mobile manipulating platform[J]. Chinese Journal of Mechanical Engineering, 2017, 30(1): 3-6.
[7] DING Xilun, YANG Fan. Study on hexapod robot manipulation using legs[J]. Robotica, 2016, 34(2): 468-481.
[8] ROY S S, PRATIHAR D K. Dynamic modeling, stability and energy consumption analysis of a realistic six-legged walking robot[J]. Robotics and Computer-Integrated Manufacturing, 2013, 29(2): 400-416.
[9] ROY S S, SINGH A K, PRATIHAR D K . Estimation of optimal feet forces and joint torques for on-line control of six-legged robot[J]. Robotics and Computer-Integrated Manufacturing, 2011, 27(5): 910-917.
[10] 董伟光, 王洪光, 姜勇. 一种轮足复合式爬壁机器人动力学建模与分析[J]. 机器人, 2015, 37(3): 264-270.
DONG Weiguang, WANG Hongguang, JIANG Yong. Dynamics modeling and analysis of a wall-climbing robot with biped-wheel hybrid locomotion mechanism[J]. Robot, 2015, 37(3): 264-270.
[11] SHAH S V, SAHA S K, DUTT J K. Modular framework for dynamic modeling and analyses of legged robots[J]. Mechanism and Machine Theory, 2012, 49: 234-255.
[12] KOMODA K, WAGATSUMA H. Energy-efficacy comparisons and multibody dynamics analyses of legged robots with different closed-loop mechanisms[J]. Multibody System Dynamics, 2017, 40(2): 123-153.
[13] DING Xilun, LI Kejia, XU Kun. Dynamics and wheel's slip ratio of a wheel-legged robot in wheeled motion considering the change of height[J]. Chinese Journal of Mechanical Engineering, 2012, 25(5): 1060-1067.
[14] KOMSUOGLU H, MAJUMDAR A, AYDIN Y O, et al. Characterization of dynamic behaviors in a hexapod robot[M]//Experimental Robotics. Berlin, Heidelberg: Springer, 2014: 667-684.
[15] GRAND C, BENAMAR F, PLUMET F, et al. Stability and traction optimization of a reconfigurable wheel-legged robot[J]. The International Journal of Robotics Research, 2004, 23(10/11): 1041-1058.
[16] 郑建华, 牛军川, 江民圣, 等. 基于Trot步态的四足机器人弹簧腿动力学分析与仿真[J]. 中南大学学报(自然科学版), 2015, 46(8): 2877-2883.
ZHENG Jianhua, NIU Junchuan, JIANG Minsheng, et al. Dynamic analysis and simulation of spring legs in quadruped robot based on trot gait[J]. Journal of Central South University(Science and Technology), 2015, 46(8): 2877-2883.
[17] DING Liang, GAO Haibo, DENG Zongquan, et al. Foot–terrain interaction mechanics for legged robots: Modeling and experimental validation[J]. The International Journal of Robotics Research, 2013, 32(13): 1585-1606.
[18] 张硕生, 余达太. 轮式移动操作机器人的动力学模型[J]. 北京石油化工学院学报, 2002, 10(2): 22-27.
ZHANG Shuosheng, YU Datai. Dynamic model of wheeled mobile manipulator[J]. Journal of Beijing Institute of Petrochemical Technology, 2002, 10(2): 22-27.
[19] 董超, 成凯, 胡文强, 等. 全地形铰接式履带车辆原地转向运动学与动力学建模[J]. 中南大学学报(自然科学版), 2017, 48(6): 1481-1491.
DONG Chao, CHENG Kai, HU Wenqiang, et al. Kinematic and dynamic modeling of all terrain articulated tracked vehicle in process of spin steering[J]. Journal of Central South University(Science and Technology), 2017, 48(6): 1481-1491.
[20] 王洪波, 徐桂玲, 胡星, 等. 四足并联腿步行机器人动力学[J]. 机械工程学报, 2012, 48(23): 76-82.
WANG Hongbo, XU Guiling, HU Xing, et al. Dynamics of quadruped walking robot with parallel leg mechanism[J]. Chinese Journal of Mechanical Engineering, 2012, 48(23): 76-82.
[21] XIN Guiyang, ZHONG Guoliang, DENG Hua. Dynamic analysis of a hexapod robot with parallel leg mechanisms for high payloads[C]//2015 10th Asian Control Conference (ASCC), 2015. Kota Kinabalu. New York, USA: IEEE, 2015: 1-6.
[22] BRUNO S, LORENZO S, LUIGI V, et al. Robotics modelling, planning and control[M]. London:Springer-Verlag, 2009: 152-158.
[23] LEE S. Dual redundant arm configuration optimization with task-oriented dual arm manipulability[J]. IEEE Transactions on Robotics and Automation, 1989, 5(1): 78-97.
（编辑 秦明阳）
收稿日期： 2019 -01 -17; 修回日期： 2019 -04 -05
基金项目(Foundation item)：国家自然科学基金资助项目(51875033) (Project (51875033) supported by the National Natural Science Foundation of China);
通信作者：郭盛，博士，教授，从事机器人学、并联机构学研究；E-mail：shguo@bjtu.edu.cn
