文章编号:1004-0609(2009)08-1403-06
2026铝合金热压缩变形流变应力行为
吴文祥1,韩 逸1,钟 皓1,乐永康1,张 辉2
(1. 苏州有色金属研究院有限公司,苏州 215026;
2. 湖南大学 材料科学与工程学院,长沙 410082)
摘 要:在变形温度为300~450 ℃、应变速率为0.01~10 s?1的条件下,在Gleeble?1500热模拟机上采用圆柱体压缩实验对2026铝合金热变形流变应力行为进行了研究。由试验得出变形过程中的真应力真应变曲线,并利用本构方程对流变应力值进行修正,进而根据修正后的应力值绘制功率耗散图。结果表明:变形过程中的应力值随温度的升高而降低,随应变速率的增大而升高,且修正后的稳态应力值高于未修正值;可用Zener-Hollomon参数的双曲正弦形式来描述2026铝合金热压缩变形时的流变应力行为;高温低应变速率条件下的功率耗散系数最大,该变形区发生了组织转变。
关键词:2026铝合金;热压缩变形;流变应力;本构方程;功率耗散图
中图分类号:TG 146.2 文献标识码: A
Flow stress behavior of 2026 aluminium alloy under hot compression deformation
WU Wen-xiang1, HAN Yi1, ZHONG Hao1, LE Yong-kang1, ZHANG Hui2
(1. Suzhou Non-ferrous Metals Research Institute, Suzhou 215026, China;
2. School of Materials Science and Engineering, Hunan University, Changsha 410082, China)
Abstract: The flow stress behavior of 2026 aluminium alloy under hot compression deformation in the temperature range of 300?450 ℃ at strain rates of 0.01?10 s?1 was investigated by cylindrical compression tests on Gleeble 1500 machine. The true stress—true strain curves were obtained in the tests. The flow stress was corrected by the constitutive equation and the power dissipation map was obtained using the corrected stress. The results show that the flow stress decreases with the increase of deformation temperature at a constant strain rate, and increases with the increase of strain rate at constant temperature. The corrected stable flow stress is generally higher than the uncorrected value. The flow stress behavior of 2026 alloy during hot compression deformation can be represented by a Zener-Hollomon parameter in the hyperbolic sine form. The efficiency of power dissipation is much higher at high temperature and low strain rate, which is associated with microstructural changes.
Key words: 2026 aluminium alloy; hot compression deformation; flow stress; constitutive equation; power dissipation map
为了适应大型飞机对蒙皮材料更高的强度和“损伤容限”要求,美铝于1999年在2024合金的基础上通过进一步控制杂质元素Fe、Si的含量以及添加微量Zr,开发出了新一代高强、高损伤容限2026合金。该合金比2024合金具有更高的“损伤容限”和强度。目前,2026合金已经作为下翼面蒙皮材料被应用到了空中客车公司的大型飞机A380上。
和其它常规铝合金一样,2026合金需经热加工成形,而在热加工变形过程中,合金流变应力是很重要的一个参数,它的大小决定了变形时所需施加的负荷大小及所需消耗的能量多少,直接影响到加工工艺的制订。热变形过程中,材料的高温流变应力σ与变形温度Tdef和应变速率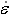 密切相关,通过引入Zener-Hollomon参数,将流变应力σ表达为Z值的指数函数关系、幂函数关系和双曲函数关系,为用Z参数研究变形条件与材料组织和性能演变的关系提供方便[1]。近年来,以塑性有限元为代表的数值模拟技术在金属塑性加工领域获得了越来越广泛的应用,获取精确的流变应力数值或本构模型是提高计算精度的关 键[2?3]。此外,流变应力还可用于计算获得材料的功率耗散图,可用来控制材料在热加工后的显微组织[4?6]。
密切相关,通过引入Zener-Hollomon参数,将流变应力σ表达为Z值的指数函数关系、幂函数关系和双曲函数关系,为用Z参数研究变形条件与材料组织和性能演变的关系提供方便[1]。近年来,以塑性有限元为代表的数值模拟技术在金属塑性加工领域获得了越来越广泛的应用,获取精确的流变应力数值或本构模型是提高计算精度的关 键[2?3]。此外,流变应力还可用于计算获得材料的功率耗散图,可用来控制材料在热加工后的显微组织[4?6]。
本文作者以铸态2026铝合金为对象,采用高温圆柱压缩法研究其热变形流变应力行为,重点考虑压缩过程中产生的变形热对流变应力的影响,并对真应力-真应变曲线进行修正,建立流变应力本构方程,绘制了功率耗散图,为铸态2026铝合金热加工工艺 的制订以及变形过程的数值模拟提供试验数据及理论指导。
1 实验
实验使用的材料是直径为120 mm的2026铝合金圆锭,其化学成分(质量分数)为:3.9%Cu,1.3%Mg,0.5%Mn,0.15%Zr,Fe和Si含量控制在0.1%以下,余量Al。铸锭经(500 ℃,24 h)均匀化处理后沿垂直长度方向截取直径为10 mm、高为15 mm的Rastegaev[7]圆柱体试样,在Gleeble?1500热模拟机上进行热压缩实验,试样的初始温度分别设为300、350、400和450 ℃,应变速率分别为0.01、0.1、1和10 s?1。压缩前,试样两端槽内填充润滑剂(75%石墨+20%机油+5%硝酸三甲苯脂),以减小试样与压头之间摩擦的影响。试样以10 ℃/s的速度加热到预设温度,并保温3 min以保证温度的均匀性,然后开始压缩,总应变量为0.7(真应变)。
2 结果与讨论
2.1 真应力-真应变曲线
2026铝合金在不同温度及应变速率条件下的真应力—真应变曲线如图1所示。从图1中可以看出,在同一应变速率条件下,随着变形温度的降低,流变应力显著增大,峰值应力所对应的真应变也逐渐增大;在同一变形温度下,随着应变速率的升高,流变应力增大。2026铝合金热压缩变形时,其流变应力的总体变化规律表现为:变形初期,流变应力随真应变的增加迅速上升,出现一峰值后逐渐降低,表现出流变软化的特征,直到基本保持恒定,这时加工硬化与流变软化达到平衡,真应力—真应变曲线趋于水平。流变软化是铝合金在高温变形过程中真应力—真应变曲线的典型特征。它是由变形热即温升或材料内部组织结构的不稳定性引起的。
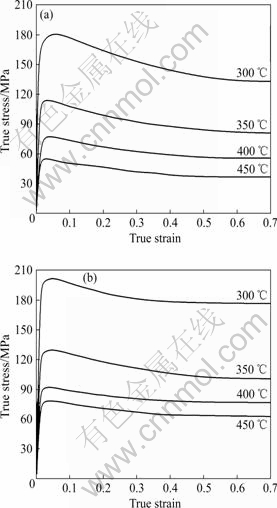
图1 不同应变速率下的真应力—真应变曲线
Fig.1 True stress—true strain curves at different strain rates: (a) 0.01 s?1; (b) 0.1 s?1
2.2 变形热对流变应力的影响
铝合金在塑性变形时所消耗的大量能量,其中绝大部分转化为热,小部分以储能的形式保留在金属中。在高应变速率下,合金变形时间短,在短时间内所产生的大量的热来不及散失,使铝合金内部温度急剧上升,造成其流变应力降低[8]。而在低应变速率条件下,合金的大部分变形热通过夹具散失到环境中,产生的温升可以忽略,基本上还是等温变形。所以,本研究中主要讨论高应变速率下的变形热对流变软化的影响。
由于在变形过程中,测量温度的电偶对的反应时间较长,因此只能测量低应变速率(即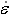 <10 s?1)的变形过程,而对于高应变速率(即
<10 s?1)的变形过程,而对于高应变速率(即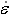 ≥10 s?1)变形过程,其测量值是不真实的。此时温升只能通过理论计算得出,并近似认为高应变速率下变形为绝热状态。本研究引入以下方程[9]计算应变速率为10 s-1时由变形热所引起的试样温升:
≥10 s?1)变形过程,其测量值是不真实的。此时温升只能通过理论计算得出,并近似认为高应变速率下变形为绝热状态。本研究引入以下方程[9]计算应变速率为10 s-1时由变形热所引起的试样温升:

式中:ρ为合金密度;C为合金比热容;?ε为应变间隔;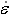 为平均应力,可表示为
为平均应力,可表示为

根据式(1)和(2)可计算出应变速率为10 s?1时各个温度以及不同应变条件下对应的试样温升?T,该试样温升?T加上试验的初始温度后即为修正后试样的实际温度值。图2所示为变形过程中试验温度的测量值(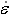 <10 s?1)和计算值(
<10 s?1)和计算值(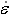 =10 s?1)。从图2中可以看出,在350 ℃变形时,随着应变速率增大,试样温度变化越来越明显,其中应变速率为10 s?1时,试样温度几乎随应变线性上升,真应变为0.7时,试样温度达到393 ℃,比预设温度350 ℃高出43 ℃。而当应变速率为0.01 s-1时,温度的变化可由热模拟机的加热系统予以补偿,试样温度在整个变形过程中基本上维持在350 ℃左右。
=10 s?1)。从图2中可以看出,在350 ℃变形时,随着应变速率增大,试样温度变化越来越明显,其中应变速率为10 s?1时,试样温度几乎随应变线性上升,真应变为0.7时,试样温度达到393 ℃,比预设温度350 ℃高出43 ℃。而当应变速率为0.01 s-1时,温度的变化可由热模拟机的加热系统予以补偿,试样温度在整个变形过程中基本上维持在350 ℃左右。

图2 预设温度350 ℃时不同应变速率下的瞬时温度
Fig.2 Instantaneous temperatures at different strain rates and pre-set temperature of 350 ℃
2.3 本构方程的建立
基于热模拟试验提供的真应力—真应变数据,可以建立流变应力本构方程。考虑到峰值应力均出现在应变较小的时刻,温升修正前后峰值变化并不明显,为方便计算,取相应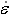 和T条件下的真实峰值应力来建立本构方程[10]。
和T条件下的真实峰值应力来建立本构方程[10]。
热变形过程中,描述流变应力的本构模型有[11?12]:
低应力状态

高应力状态

所有应力状态
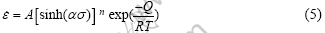
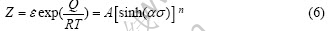
式中:A1、A2、A、n、n1、α和β均为常数;T为绝对温度;Q为热变形激活能;R为气体常数;Z为Zener-Hollomon参数。式(5)中α是可调常量,且满足α=β/n1。
假定变形激活能Q与温度T无关,对式(5)两边取对数后偏微分可得
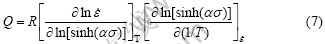
图3和4所示分别为在热压缩过程中峰值应力与应变速率和变形温度的关系。由图3和4中所示直线的斜率可以得出n1=11.795,β=0.142,进而计算出α=β/n1=0.012 mm2/N,变形激活能Q=370.8 kJ/mol,应力指数 =10。
=10。
对式(6)两边取对数得

图5所示为lnZ—ln[sinh(ασ)]关系曲线。采用一元线性回归分析可得出两者的关系为:lnZ=60.16+ 9.71ln[sinh(ασ)],相关系数达0.99。由此,可求得材料常数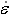 值为1.34×1026。显然,2026合金流变应力双曲正弦项的自然对数和Z参数的自然对数间满足线性关系,即可以用双曲正弦模型来描述2026铝合金热压缩变形流变应力行为。
值为1.34×1026。显然,2026合金流变应力双曲正弦项的自然对数和Z参数的自然对数间满足线性关系,即可以用双曲正弦模型来描述2026铝合金热压缩变形流变应力行为。
2.4 功率耗散图及流变应力的修正
根据动态材料学模型的观点[13],材料的加工过程可看作为一个能量消耗系统,总功率包含两个互补函数G(耗散量)和J(耗散协量)。G值代表由于塑性变形引起的功率消耗,J是材料变形过程中组织变化引起的功率消耗。这两种能量所占比例由材料在一定应力下的应变速率敏感指数m决定。

图3 应变速率与峰值应力的关系
Fig.3 Relationship between strain rate and peak stress: (a) ln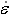 —lnσ; (b) ln
—lnσ; (b) ln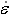 —σ; (c) ln
—σ; (c) ln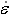 —ln[sinh(ασ)]
—ln[sinh(ασ)]
在给定的温度和应变下,J可表示为[14]
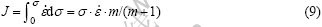
当材料处于理想线性耗散状态(m=1)时,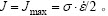
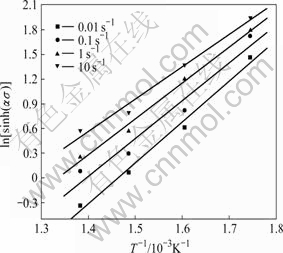
图4 峰值应力与变形温度的关系
Fig.4 Relationship between peak stress and deformation temperature

图5 lnZ与ln[sinh(ασ)]的关系
Fig.5 Relationship between lnZ and ln[sinh(ασ)]
功率耗散系数可用一个无量纲参数表示,即

功率耗散图由功率耗散系数的等值线组成,反映了材料在热加工过程中的功率耗散特征,代表热加工变形过程中的显微组织变化率。从功率耗散图中可直接分析不同区域的变形机制,如动态再结晶和动态回复等。
为了绘制稳态流变条件下的功率耗散图,需要知道稳态流变应力值。而由前面的分析可知,变形热引起材料内部温度的升高,造成稳态流变应力值降低,因此,为了获得等温变形条件下的稳态流变应力值,需要对高应变速率下的稳态流变应力进行修正。DEVADAS等[15]研究结果表明,温度变化对合金流变应力的影响可表示为

图6所示为应变速率为10 s?1条件下修正的应力—应变曲线与未修正的应力—应变曲线的对比。从图6中可以看出,修正前后应力—应变曲线的走向基本一致,且在低应变下,两曲线基本重合,但到达峰值应力后,修正曲线就明显高于未修正曲线。在应变速率为10 s?1的条件下,当温度为300 ℃且应变达到0.7时,修正与未修正应力值相差最大,为20.4 MPa。而且,随着变形温度的升高,变形热减少,这种差值也逐渐减小。另外,从图6中还可以看出,即使引入了变形热的修正,修正后的流变曲线仍然表现出流变软化的特征,这可能是因为发生了动态再结晶的缘故。
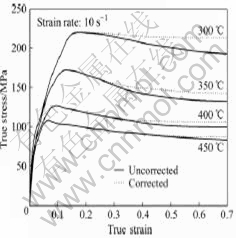
图6 修正前后的真应力—真应变曲线的对比
Fig.6 Comparison between corrected and uncorrected true stress—true strain curves
根据修正后的流变应力值,采用3次样条函数拟合流变应力lnσ与ln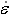 的函数关系,并根据式(10)可得出功率耗散系数η。图7所示为真应变为0.6时的功率耗散图。其它应变条件下的功率耗散图与此类似。
的函数关系,并根据式(10)可得出功率耗散系数η。图7所示为真应变为0.6时的功率耗散图。其它应变条件下的功率耗散图与此类似。
从图7可以看出,随应变速率增大,功率耗散系数逐渐降低。在低应变速率0.01 s?1条件下,尤其在450 ℃高温变形区域,功率耗散系数值最大,约为0.39,表明该区域发生了组织转变,如动态再结晶、动态回复等。有研究表明[16],金属的热变形激活能与自扩散激活能相近时,容易发生动态回复;而当热变形激活能比自扩散激活能大得多时,容易发生动态再结晶。本试验得出的2026铝合金的热变形激活能约为370.8 kJ/mol,远远高于自扩散激活能,也可以推断出合金在变形过程中发生了动态再结晶。相关机理有待进一步研究。
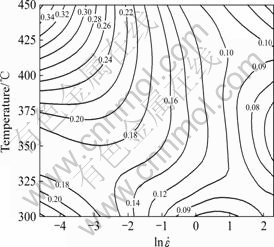
图7 2026铸态合金在应变为0.6时的功率耗散图
Fig.7 Power dissipation map of as-cast 2026 alloy at strain of 0.6
3 结论
1) 2026铝合金热压缩变形过程中,流变应力随变形温度的升高和应变速率的降低而减小。高应变速率下,变形热引起试样温度升高,试验记录的流变应力曲线为非恒温条件下的结果;对高应变速率下的流变应力进行修正后显示,随着应变量的增大,修正前后的流变应力差值逐渐增大。
2) 2026铝合金热变形峰值流变应力满足双曲正弦本构关系式,其材料常数为α=0.012,n=10,A= 1.34×1026,其平均热变形激活能为370.8 kJ/mol。
3) 高温低应变速率变形区域,即变形温度为450 ℃、应变速率为0.01 s?1的区域,功率耗散系数最大,约为0.39,可能发生了动态再结晶等组织转变。
REFERENCES
[1] CERRI E, EVANGELISTA E, MCQUEEN H J. Overview of the high temperature substructure development in Al-Mg alloys [J]. High Temperature Materials and Processes, 1999, 18: 227?240.
[2] ZHANG H, YANG L B, PENG D S, LIN G Y. Numerical simulation on microstructural evolution during multipass hot-rolling of aluminum alloys[J]. Trans Nonferrous Met Soc China, 2001, 11(2): 231?234.
[3] GRONOSTAJSKI Z. The constitutive equations for FEM analysis[J]. Journal of Materials Processing Technology, 2000, 106: 40?44.
[4] 黄光胜, 汪凌云, 陈 华, 黄光杰, 张所全. 2618铝合金的热变形和加工图[J]. 中国有色金属学报, 2005, 15(5): 763?767.
HUANG Guang-sheng, WANG Ling-yun, CHEN Hua, HUANG Guang-jie, ZHANG Suo-quan. Hot deformation and processing maps of 2618 aluminum alloy[J]. The Chinese Journal of Nonferrous Metals, 2005, 15(5): 763?767.
[5] MURTY S V S N, RAO B N, KASHYAP B P. Development and validation of a processing map for AFNOR 7020 aluminium alloy[J]. Materials Science and Technology, 2004, 20: 772?782.
[6] GRONOSTAJSKI Z. The deformation processing map for control of microstructure in CuAl9.2Fe3 aluminium bronze[J]. Journal of Materials Processing Technology, 2002, 125/126: 119?124.
[7] 沈 健. 2091铝锂合金高温塑性变形行为研究[D]. 长沙: 中南工业大学, 1996.
SHEN Jian. Study on the plastic deformation behavior of 2091 AI-Li alloy at elevated temperatures[D]. Changsha: Central South University of Technology, 1996.
[8] LI L, ZHOU J, DUSZCZYK J. Determination of a constitutive relationship for AZ31B magnesium alloy and validation through comparison between simulated and real extrusion[J]. Journal of Materials Processing Technology, 2006, 172: 372?380.
[9] BARAGAR D L. The high temperature and high strain rate behavior of a plain carbon and an HSLA steel[J]. J Mech Work Technol, 1987, 14: 295?307.
[10] ZHANG H, LI L, YUAN D, PENG D. Hot deformation behavior of the new Al-Mg-Si-Cu aluminum alloy during compression at elevated temperatures[J]. Materials Characterization, 2007, 58: 168?173.
[11] SPIGARELLI S, EVANGELISTA E, MCQUEEN H J. Study of hot workability of a heat treated AA6082 aluminum alloy[J]. Scripta Materialia, 2003, 49: 179?183.
[12] BERGSMA S C, KASSNER M E, LI X, WALL M A. Strengthening in the new aluminum alloy AA6069[J]. Mater Sci Eng A, 1998, 254: 112?118.
[13] BOZZINI B, CERRI E. Numerical reliability of hot working processing maps[J]. Mater Sci Eng A, 2002, 328: 344?347.
[14] PRASAD Y V R K, GEGAL H L, DORAIVELU S M, MALAS J C, MORGAN J T, LARK K A, BARKER D R. Modelling of dynamic material behaviour in hot deformation: forging of Ti-6242[J]. Metall Trans A, 1984, 15: 1883?1890.
[15] DEVADAS C, BARAGAR D, RUDDLE G, SAMARASEKERA I V. Thermal and metallurgical state of steel strip during hot rolling: Part II. Factors influencing rolling loads[J]. Metall Trans A, 1991, 22(2): 321?333.
[16] KANTER J J. The problems of a temperature coefficient of tensile creep rate[J]. Trans.AMEI, 1938, 131: 385?404.
基金项目:中国铝业股份有限公司科研计划资助项目(CHALCO-2007-KJ-06)
收稿日期:2008-07-11;修订日期:2008-11-19
通讯作者:吴文祥,工程师;电话:0512-88856525;E-mail: wwx985@163
(编辑 何学锋)