Impacts of optimization strategies on performance, power/energy consumption of a GPU based parallel reduction
来源期刊:中南大学学报(英文版)2017年第11期
论文作者:Phuong Thi Yen Lee Deok-Young Lee Jeong-Gun
文章页码:2624 - 2637
Key words:parallel reduction; GPU; code optimization; power; energy; voltage frequency scaling
Abstract: In the era of modern high performance computing, GPUs have been considered an excellent accelerator for general purpose data-intensive parallel applications. To achieve application speedup from GPUs, many of performance-oriented optimization techniques have been proposed. However, in order to satisfy the recent trend of power and energy consumptions, power/energy-aware optimization of GPUs needs to be investigated with detailed analysis in addition to the performance-oriented optimization. In this work, in order to explore the impact of various optimization strategies on GPU performance, power and energy consumptions, we evaluate performance and power/energy consumption of a well-known application running on different commercial GPU devices with the different optimization strategies. In particular, in order to see the more generalized performance and power consumption patterns of GPU based accelerations, our evaluations are performed with three different Nvdia GPU generations (Fermi, Kepler and Maxwell architectures), various core clock frequencies and memory clock frequencies. We analyze how a GPU kernel execution is affected by optimization and what GPU architectural factors have much impact on its performance and power/energy consumption. This paper also categorizes which optimization technique primarily improves which metric (i.e., performance, power or energy efficiency). Furthermore, voltage frequency scaling (VFS) is also applied to examine the effect of changing a clock frequency on these metrics. In general, our work shows that effective GPU optimization strategies can improve the application performance significantly without increasing power and energy consumption.
Cite this article as: Phuong Thi Yen, Lee Deok-Young, Lee Jeong-Gun. Impacts of optimization strategies on performance, power/energy consumption of a GPU based parallel reduction [J]. Journal of Central South University, 2017, 24(11): 2624–2637. DOI:https://doi.org/10.1007/s11771-017-3676-5.
J. Cent. South Univ. (2017) 24: 2624-2637
DOI: https://doi.org/10.1007/s11771-017-3676-5

Phuong Thi Yen1, Lee Deok-Young2, Lee Jeong-Gun1
1. Smart Computing Lab., Department of Computer Engineering, Hallym University, Chuncheon 24252, Korea;
2. College of General Education, Hallym University, Chuncheon 24252, Korea
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2017
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2017
Abstract: In the era of modern high performance computing, GPUs have been considered an excellent accelerator for general purpose data-intensive parallel applications. To achieve application speedup from GPUs, many of performance-oriented optimization techniques have been proposed. However, in order to satisfy the recent trend of power and energy consumptions, power/energy-aware optimization of GPUs needs to be investigated with detailed analysis in addition to the performance-oriented optimization. In this work, in order to explore the impact of various optimization strategies on GPU performance, power and energy consumptions, we evaluate performance and power/energy consumption of a well-known application running on different commercial GPU devices with the different optimization strategies. In particular, in order to see the more generalized performance and power consumption patterns of GPU based accelerations, our evaluations are performed with three different Nvdia GPU generations (Fermi, Kepler and Maxwell architectures), various core clock frequencies and memory clock frequencies. We analyze how a GPU kernel execution is affected by optimization and what GPU architectural factors have much impact on its performance and power/energy consumption. This paper also categorizes which optimization technique primarily improves which metric (i.e., performance, power or energy efficiency). Furthermore, voltage frequency scaling (VFS) is also applied to examine the effect of changing a clock frequency on these metrics. In general, our work shows that effective GPU optimization strategies can improve the application performance significantly without increasing power and energy consumption.
Key words: parallel reduction; GPU; code optimization; power; energy; voltage frequency scaling
1 Introduction
Recently, a GPU has been a very popular platform for high performance computing (HPC). The high performance operations of a GPU are realized by a massively parallel multi-core architecture that uses SIMT (single instruction, multiple threads) vector operations. In particular, a modern GPU architecture focuses on throughput improvement by launching massively parallel threads on the hundreds or thousands of simple cores in a GPU instead of increasing core clock frequencies. This new design style of GPU processor architectures is very different from conventional high-performance CPU processor core design that has been focused on improving the latency performance of single or few threads. Furthermore, a wide range of optimization strategies for GPU-based applications have been studied in previous researches. Their work provided some good understanding on the relationship between GPU architectural features and kernel execution behavior.
The range of GPU applications has been extended continuously to cover wider general purpose data intensive and scientific computation with better power and energy efficiencies. More recently, GPU devices have been used much more effectively in modern data- centers and supercomputer computing on how much serious power and energy limitations are imposed due to increased cooling cost. In consequence, much in-depth investigations on the GPU power and energy consumptions is necessary for the applications that are executed under given power or energy budgets while satisfying their high-performance requirements.
As a subject of growing interests, our study addresses the relations between code optimization and performance/power consumption on the three different modern GPU architecture generations having different architectural features. We consider both aspects: software optimization (i.e., code optimization) and voltage frequency scaling (VFS) technique (hardware optimization) on a GPU to investigate their effects on performance, power and energy. Rather than the hardware optimization techniques such as frequency/ voltage scaling, software code optimization strategies can play a more important role in improving application performance on a GPU.
In this work, we perform experiments on a popular parallel reduction code by using CUDA on various GPU devices. Many different and independent parallel optimization techniques are applied to the basic kernel code in order to examine their impacts on the target metrics. Application execution times and power consumptions are measured with different GPU clock frequencies and memory frequency settings. The comparative analysis is performed among the differently optimized versions of a kernel code with different GPU architecture generations whose characteristics are different from each other.
In short, our study makes the following contributions.
1) The paper analyzes different types of parallel optimization techniques in details and indicates what GPU architectural features affect performance and power/energy as well as how much the performance and power/energy can be improved by varying them.
2) The paper presents a large set of experiments to answer the question, how the optimization strategies affect the power and energy of a GPU under different core clock frequency settings.
3) Our study provides a deep understanding on the effect of optimization techniques and classifies the degree of their impacts on performance and power/energy efficiency of our target application on three different Nvidia GPU architecture generations (Fermi, Kepler and Maxwell architectures).
The remainder of this paper is organized as follows. Section 2 presents the related work. Background for our work is described in Section 3. Section 4 presents the implementation details of our target application on a GPU. The experimental results and analysis are described in Section 5. Finally, Section 6 concludes the paper.
2 Related work
There have been a number of studies focusing on the effects of architecture designs and optimizations on application performance. Their works have provided a thorough understanding on how performance and kernel behavior depends on memory access pattern and optimization techniques by conducting experiments on a set of benchmarks from diverse application domains on a single or multiple GPU architectures [1–5]. Some other work has focused on GPU power measurement methodologies [6–10] and GPU power/energy modeling [11–17]. A DVFS technique on a GPU for power and energy efficiency has been also studied [18–20]. However, there has been little work on the effects of code optimizations on all three aspects, i.e., application performance, GPU power and energy consumption. The studies that are probably most related to our studies are presented in the work [21, 22]. UKIDAVE et al [21] have conducted a performance analysis of different optimization techniques on four different fast Fourier transform (FFT) implementations by using OpenCL on discrete GPUs, shared memory GPUs (APUs) and low power system-on-chip devices. They observed 11% variation in energy consumption among different optimizations. They also have stated that different algorithms implementing the same application can perform with vast differences according to the target hardware. COPLIN et al [22] have studied 128 versions of two different n-body solutions running on five GPU configurations using three clock frequency settings. They applied six optimization techniques in each kernel program to observe their effects on application performance, GPU power and energy consumption. Their analysis showed that code optimizations tend to increase the power consumption and have large impact on energy.
As an extended and in-depth version of the previous existing studies, we investigate the impact of GPU optimization techniques on the performance, power and energy consumption of a fundamental and primitive parallel algorithm, i.e., “parallel reduction”, by exploring hardware/software design space spanned by “various optimization techniques”, “GPU core clock frequency” as well as “memory frequency settings”. Moreover, we make a comparative analysis with different “GPU architectures” of three Nvidia GPU generations to examine the impact of a GPU’s internal architecture design on the application performance as well as power and energy consumption.
3 Background
3.1 Target application
In this work, we use “parallel reduction” for our target application. A “reduction” function is a well- known and frequently employed kernel function for many data-intensive processing applications. The reduction can be used when an array of values needs to be reduced to a single value using a binary associative operator (i.e., sum, min and max). The reduction function can be used to accelerate statistical computations, such as mean and standard deviation derivations. Another reason why we choose this kernel is that there have been many well developed optimization strategies available for the reduction on GPUs [2, 23]. The visual demonstration of a reduction operation is illustrated in Fig. 1.
We evaluate performance and power consumption of the seven different versions of the parallel reduction kernel by applying different optimization techniques step by step on GPUs. The brief summary of the seven reduction kernels is described in Table 1.

Fig. 1 A reduction algorithm with binary “+” operations
Table 1 Summary of parallel reduction kernels [23]

The kernel code RK-1 is an initial reduction kernel code in which any code optimization is not applied (except the use of a shared memory). The problem in the RK-1 is characterized by “interleaved addressing with divergent branching”. The first optimization is applied to make an improved version of the kernel, RK-2, by replacing the heavy modulo operations and resolving “divergent branching” with strided indexing and non-divergent branching. However, the optimized kernel, RK-2, still has a problem of serious “bank conflict” [23].
To solve the memory bank conflicts, “sequential addressing” is applied to the thread indexing of the RK-2. The kernel code without the bank conflicts is devised with the sequential addressing and it is named as RK-3. Then, to improve thread utilization in the RK-3 where only half of the threads work in the first loop of reduction, an optimization called “first add during load” is employed in kernel RK-4. After that, by applying “partial unrolling” (unroll last warp) to kernel RK-4, kernel RK-5 is derived [23].
In order to reduce the overhead of control instruction overhead in kernel RK-5, further optimization is applied to kernel RK-6 by using “completely unrolling” technique. As a final optimization, workload balancing based on “Brent’s Theorem” is applied to RK-6 to generate a kernel RK-7, where there is an optimal balancing between the number of threads and the workload of a single thread [23]. The implementation details of each kernel on a GPU are presented in Section 4.
3.2 GPU architecture and CUDA
In general, a GPU architecture is made of a scalable number of streaming multiprocessors (SMs the name, SM, is used in a Fermi GPU architecture. The improved versions of the SM architecture are named SMX in a Kepler architecture and SMM in a Maxwell architecture), and each SM contains a number of parallel processing cores (stream processors, SPs), warp schedulers, dispatch units, special function units (SFUs), local memory, shared memory, texture memory, L1, L2 caches and constant cache. A GPU board has a high-bandwidth off-chip global memory, known as a graphic DDR (GDDR) DRAM, up to several gigabytes in size. The most recent GPU is announced to include a 12 GB global memory [24]. An on-chip shared memory provides high speed memory accesses as fast as a register and a part of the shared memory can be configured manually into an L1 cache. Both constant memory and texture memory are placed in a global memory but they are cached. Reading data from a constant cache is as fast as a register if all threads read the same address.
A group of 32 threads, called a “warp” is scheduled and executed together, meaning that the same instruction is applied to all 32 threads (single-instruction multiple- thread, SIMT). In a GPU, accessing an off-chip global device memory takes hundreds of clock cycles. However, a GPU is designed to hide the long off-chip memory access latency by supporting massive multi-threading with fast hardware based warp switching. It implies that the off-chip memory access latency can be hidden as long as there are enough active warps to keep cores busy.
Supported on Nvidia GPUs, CUDA (computed unified device architecture) is a data parallel programming model. The host program launches a sequence of kernels with implicit barrier synchronizations between kernels. Each kernel is organized as a hierarchy of light weight parallel threads which are grouped into blocks. A set of blocks are grouped into a grid that executes a kernel function. Each thread or block has unique index in the grid. The number of threads in a block is specified by programmers; however, the number of blocks that can run on one SM is determined by the available resources of the SM and the resource requirements of blocks. The challenge for programmers is to optimize a CUDA code so that it exposes enough parallelism to make full use of the SIMD architecture, exploit the full bandwidth of a device memory and maximize the utilization of a shared memory in an SM and a data cache efficiently for a given GPU architecture.
Developers have been exhaustively searching for optimization strategies in such a way that a GPU can be effectively and efficiently utilized. It is most performance critical to do memory optimizations such as data transfer optimization between host and device, and optimal placement of data onto the memories with different performance characteristics and different hierarchy levels. Of course, conventional code optimizations such as operator strength reduction, precision reduction and instruction scheduling can also make further performance improvement for applications running on a GPU.
4 Parallel reduction implementation on a GPU
From Fig. 1, it is easy to see that with ‘N’ number of data, a sequential reduction has ‘N–1’ operations with the time complexity of O(N). The step complexity of a parallel reduction is O(lgN), where each time step ‘s’ computes ‘N/2s’ independent instructions. With ‘P’ physical processors working in parallel, the time complexity of the parallel reduction becomes O(N/P+lgN). An efficient algorithm should have an optimally distributed and balanced workload among processors so that it can achieve high efficiency at the viewpoint of “cost” (Generally, the cost of a parallel application is defined by a product of time complexity and the number of deployed processors).
The general implementation of a parallel reduction on a GPU is to decompose its computation into multiple thread blocks. The partial results between the blocks then become input data for the next round of kernel invocations. This is called a recursive kernel invocation. Note that there is a need to do a local synchronization among threads in a “thread block” as well as a global synchronization after each block finishes its task. The implementation of the parallel reduction on a GPU can be illustrated in Fig. 2. Our optimization goal is to strive for the GPU peak memory bandwidth in order to maximize performance.
As mentioned above, the reduction application is implemented in seven different kernels with various code optimization strategies. Each kernel is a step-by-step optimized version compared to the proceeding kernel. This section revisits in details how the reduction is parallelized on a GPU platform by using CUDA programming and how each optimization technique is applied in each kernel [23].
4.1 Kernel RK-1
The computing flow of the algorithm used in kernel RK-1 is illustrated in Fig. 3. It uses a shared memory with interleaved addressing. At first, each thread loads one element from a global memory to the shared memory. Then the threads whose index is divisible by the stride, ‘2s’, only do the computations at the step, ‘s’, until the final reduced single value is found. This algorithm exhibits a high degree of “warp divergence” with the control flow which depends on the thread index and therefore it is very inefficient. Furthermore, it also uses “modulo” operator which has very low instruction throughput [23].
Later, in Section 5.2, it will be shown that the inefficient thread execution with the warp divergence introduces higher power consumption than the other optimized kernel functions. This is somewhat contrary to the fact that the optimization tends to increase power consumption slightly more.
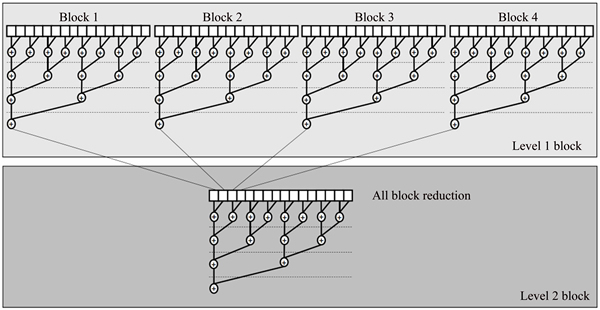
Fig. 2 Parallel reduction implementation on GPU by using CUDA
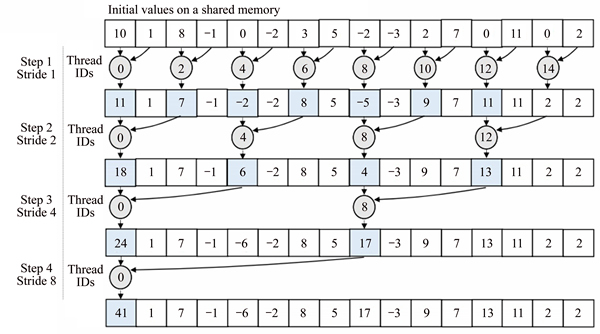
Fig. 3 Kernel RK-1 algorithm
4.2 Kernel RK-2
In kernel RK-2, the divergent branch in the previous kernel is replaced by a strided index. The kernel RK-2 algorithm is illustrated in Fig. 4. The use of the strided indexing can avoid the problematic divergent branch and therefore its usage can improve performance significantly. However, this kernel still suffers from the “bank conflicts” in a shared memory where multiple threads from a warp accesses the memory addresses assigned to a single memory bank [23]. This results in n-way bank conflicts which degrade the memory bandwidth. For an example, 2-way bank conflict can be as illustrated as shown in Fig. 5.
4.3 Kernel RK-3
To resolve the bank conflict happening in the previous kernel due to interleave addressing, the kernel RK-3 uses sequential addressing which supports conflict-free shared memory accesses. The shared memory access pattern of the RK-3 algorithm is shown in Fig. 6. However, thread ID-based indexing of this kernel causes half of the threads to be idle on the first loop iteration. As the number of iterations increases, the number of active threads is continuously reduced by half. In consequence, the thread utilization becomes significantly lowered and the GPU resources used in the threads are wasted. Finally, it causes performance degradation.
4.4 Kernel RK-4
Kernel RK-4 overcomes the problem of low thread utilization by conducting the first step of reduction when reading data from a global memory. Instead of just copying a single data from global memory to shared memory, each thread performs the addition on two elements read from global memory and then writes the result to shared memory. The optimization strategy used in Kernel RK-4 is therefore called “first add during load” and it is illustrated in Fig. 7 [23].
4.5 Kernel RK-5
As mentioned previously, the reduction algorithm has low arithmetic intensity; therefore, the bottleneck of the kernel can be caused by the instruction overhead incurred from loop control instructions. The kernel RK-5 uses the “loop unrolling” technique to reduce the control instruction overhead and to improve the performance [23].
Due to the fact that thread synchronization primitive, __synthreads(), is unnecessary when the number of active threads is less than 32, the codes of the threads in the last warp can be unrolled to remove unnecessary synchronization function calls from the threads of the last warp in every block.
4.6 Kernel RK-6
The loop unrolling method can be applied to the reduction algorithm entirely as long as the number of iterations is known. By using “Template” parameter and “switch” statement in the host code, the block size is known at compile time, which makes it possible to completely unroll the reduction [23]. This method can achieve optimal performance for any (power of 2) number of threads.
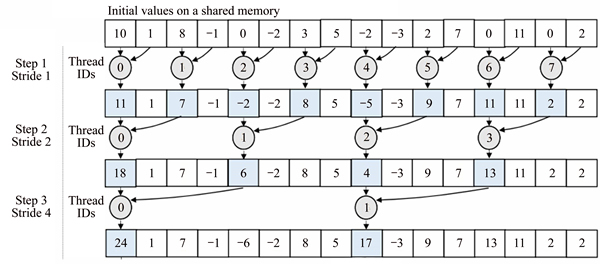
Fig. 4 Kernel RK-2 algorithm
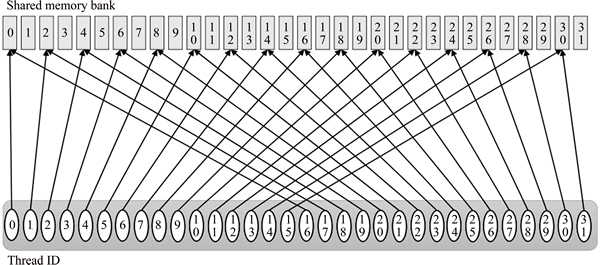
Fig. 5 2-way bank conflict problem
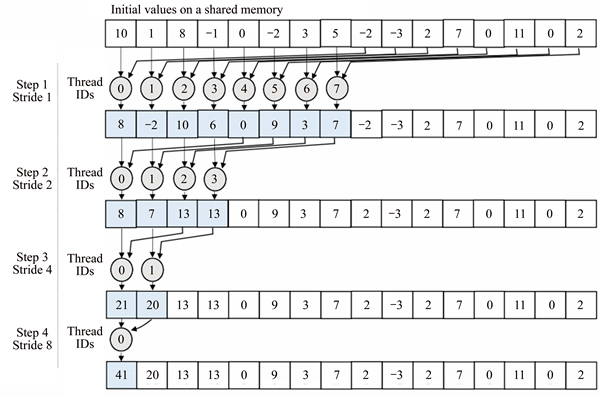
Fig. 6 Kernel RK-3 algorithm
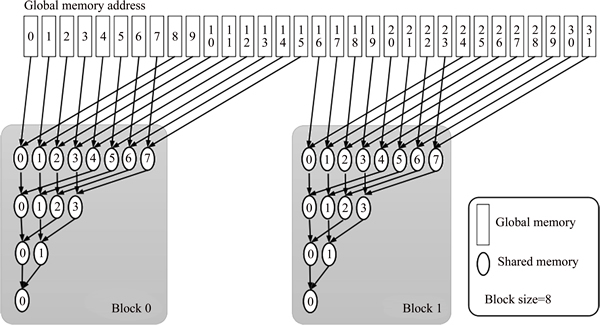
Fig. 7 Kernel RK-4 algorithm
4.7 Kernel RK-7
As mentioned previously, with N number of data, an optimal kernel code should be able to produce a cost-efficient algorithm. The cost of a parallel algorithm is calculated by the multiplication of “number of utilized processors” and the corresponding “time complexity” obtained with the number of processors. Assuming that the algorithm has N number of threads (processors) and time complexity is O(lgN), the cost is O(N lgN), which is not cost-efficient.
A “Brent’s theorem” has been well known in a parallel computing society and it suggests that the cost of the algorithm becomes O((N/lgN)×lg N)=O(N), which is cost-optimal when each of N/lgN number of threads does O(lg N) initial sequential work, and then all threads cooperate for O(lg N) steps in parallel. In this case, the time complexity is O(lg N) which is approximating O(lg N) in the first sequential computing phase and O(lg N) in the later parallel computing phase. This optimization strategy is called “algorithmic cascading”. Therefore, by employing Brent’s theorem in our parallel reduction, in addition to the add operations of the two elements read directly from global memory at the first step, each thread now should sum multiple elements further with a sequential while-loop iteration at the initial phase of thread computation. To maintain “coalescing memory address”, the while-loop should be incremented by a gridSize step.
4.8 Hardware platform and experimental setup
The aim of our work is to investigate the behaviors and patterns of performance and power/energy consumption of a target kernel code with different optimization strategies and various GPU operating conditions. We carried out experiments and collected the performance and power data from the seven versions of a reduction kernel code under different GPU frequency settings. Based on the experimental results, we conducted an in-depth analysis to show the impact of optimization techniques as well as VFS on reduction kernel executions.
We attempt to measure the GPU power and system power (including both the CPU power and GPU power). The details of our experimental platforms and measurement tools are described in Table 2. To measure dynamic GPU power, a GPU-Z video card information utility is used. This lightweight system software is integrated with sensors that can trace vital runtime GPU information such as instant GPU core clock, memory clock, temperature, fan speed, GPU load, voltage and our parameter of interest, power consumption (as a percentage of TDP). The data can be logged into a file at a sampling rate ranging from 0.1 Hz to 10 Hz. To measure system power, an “Extech”' power analyzer instrument is used. This instrument provides basic information such as system power, power factor, voltage, current, phase angle, and frequency. Data can also be logged to files in a profiling computer system at a maximum sample rate of 2 Hz. The Extech power analyzer is powered by an independent power supply, and thus has no influence on our system power consumption measurement. The hardware and system configurations for our power measurement are shown in Fig. 8.
Table 2 Experimental platforms and measurement tools
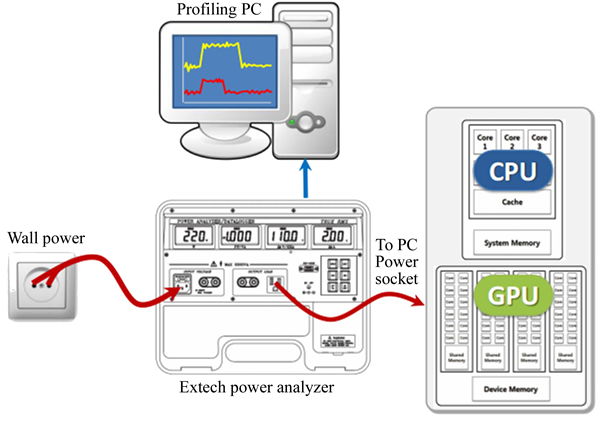
Fig. 8 Experimental hardware setup
The reduction application is implemented on three representative high-end GPU devices of three Nvidia GPU generations (Fermi, Kepler and Maxwell) with the configurations which are described in Table 3. The VFS experiments are performed by using the Nvidia Inspector. The core frequency and memory frequency are properly adjusted for the sake of stability and reliability of the GPU executions on each GPU device. While changing one frequency component, the other frequency component is fixed at its default value. In this study, the collected data are sampled at 2 Hz (0.5 s) and the time stamps of the GPU power consumption are recorded as a pair of data. For more stabilized, accurate measurements, our kernels are iterated over a number of loops so that our application can last for more than 10 s and the stable sample values of GPU power consumption are recoded.
5 Experiment results and analysis
In this section, we compare and analyze the performance and GPU power consumption of reduction kernels from RK-1 to RK-7, which are optimized step by step with different optimization strategies.
5.1 Performance analysis on optimization strategies
5.1.1 Impact of optimization strategies
Figure 9 and Table 4 show the memory bandwidth and the speedup at each step as well as accumulative speedup of seven reduction kernels on three GPUs at their default settings, respectively. From Nvidia visual profiler statistics, the first kernel RK-1 exposes a high degree of warp divergence as much as 73.4%. The number of inactive threads out of total launched threads is as high as 83% and that means very low thread utilization. Since all of the threads in a warp share a program counter, the warp divergence in a warp causes the executions of all the instructions in the both true and false paths of the divergent branching. This working behavior of the divergence increases the total number of instructions executed for the warps. Due to the increased number of instructions, more instruction fetch capability is required. Finally the main reason for the stall of preventing the warps from executing comes from the saturated instruction fetch.
In consequence, it lowers warp execution efficiency which leads to inefficient use of the GPU’s computing resources. The second kernel RK-2, which replaces the divergent branch by a strided index, significantly reduces the warp divergence to 7.8% and the percentage of the inactive threads to 33%. This kernel pushes up the performance by 76% on average.
Table 3 GPUs’specifications
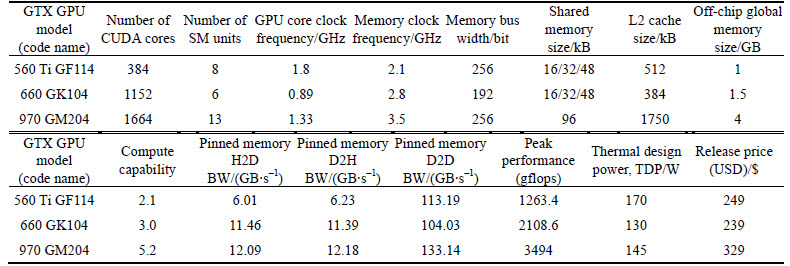
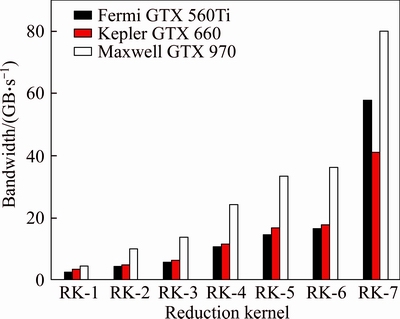
Fig. 9 Performance of reduction kernels on all GPUs at default settings
As mentioned previously, although RK-2 kernel is optimized with non-divergent indexing, it still suffers from a bank conflict problem due to interleave addressing. In GTX 560 (compute capability 2.1), the number of shared load/stored transactions/access=3.9 while in GTX 660 and GTX 970 (compute capability 3.0 and 5.2, respectively), the number of shared load/stored transactions/access=2.2 (Ideally transactions/access=1). It results in only 17% shared memory efficiency. Kernel RK-3 resolves this problem with sequential addressing. This improves the shared memory efficiency up to 42.3% and the total performance to 33% on average.
The percentage of inactive threads out of total threads in kernel RK-3 still remains at 33%. Kernel RK-4 overcomes the problem of low thread utilization by performing “first add during load”. Consequently, the performance is improved by 81% on average.
Another major reason for instruction stalls is thread synchronization. Figure 10 shows the break-down for the reasons of the stalls which are observed during the entire execution of the kernel RK-4 and kernel RK-5. When number of the active threads is less than 32, thread synchronization is unnecessary. Therefore, the last warp can be unrolled to improve the performance without synchronization. As shown in Fig. 10, the percentage of the stalls caused by the thread synchronizations is reduced by half in kernel RK-5 compared to that in kernel RK-4. Thanks to the significant reduction of the synchronization induced stalls, the performance is increased by 39% on average.
In the kernel RK-6, the method of completely unrolling is applied. This increases warp execution efficiency from 24% to 46.7%. As a result, on average, 9% improvement in performance is achieved.
The last kernel RK-7, utilizing algorithmic cascading, employs the Brent’s theorem. Each thread load multiple value from global memory, does multiple additions and stores the result to shared memory. In this way, we can increase workload of each thread while reducing the number of threads to make a performance-cost balance between work done by each thread and the number of threads. Then, the balancing can lead to a cost-efficient or cost-optimal algorithm.
Table 4 Step and accumulative speedups of seven kernels on three GPUs
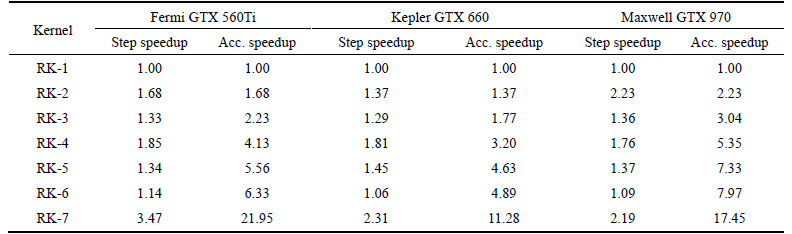
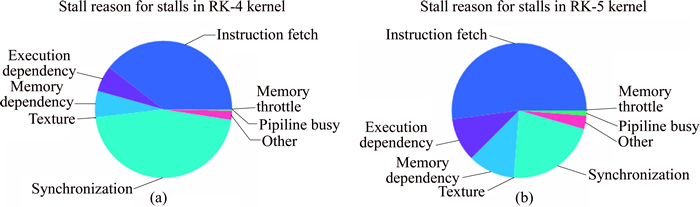
Fig. 10 Break-down stall reasons for kernel RK-4 (a) and kernel RK-5 (b)
Figure 11 shows the percentage of compute and memory utilization of kernel RK-6 and kernel RK-7. As shown in Fig. 11, this balancing optimization significantly improves the memory bandwidth utilization of GPU resources. On average, the performance is increased by 165%. Overall, the accumulative speedup values are 21.9X, 11.28X and 17.45X on GTX 560Ti, GTX 660 and GTX 970, respectively.
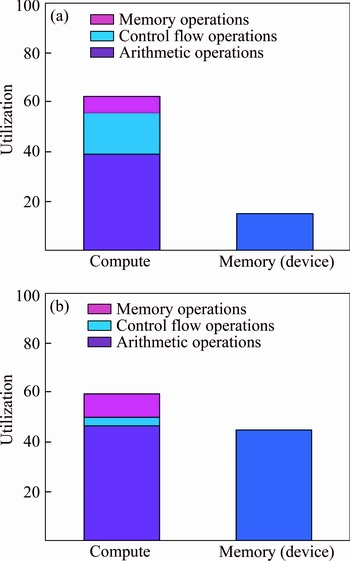
Fig. 11 Compute and memory utilization of kernel RK-6 (a) and kernel RK-7 (b)
5.1.2 Impact of three GPU generations
As shown in Table 4, the speedups observed at each corresponding step among the three GPU generations are almost the same. It implies that in general the optimization techniques affect performance on three GPU generations in almost the same way. However, there are two exceptions: 1) the first case is that the speedup of kernel RK-2 on GTX 970 is 2.23X, much greater than that on GTX 560Ti (1.68X) and GTX 660 (1.37X) and (2) the second case is that the speedup of kernel RK-7 on GTX 560Ti is 3.47X, much greater than that on GTX 660 (2.32X) and GTX 970 (2.19X).
The first case implies that on Maxwell architecture (GTX 970) the warp divergence has a higher impact on the GPU performance than other two GPUs. Therefore, it is important to avoid this problem to achieve much better throughput when the application is accelerated on Maxwell GPUs.
In the second case, the cost-effective algorithm of kernel RK-7 works well on Fermi architecture (GTX 560Ti), where the kernel performance is significantly enhanced with the highest step speedup and accumulative speedup among three GPUs. Especially, the throughput of kernel RK-7 on GTX 560Ti is higher than that on GTX 660 by 40% (It is a reverse case where GTX 660 normally performs better than GTX 560Ti on other kernels). This implies that the balancing between thread granularity and the number of threads has a big effect on Fermi architecture and therefore it can significantly accelerate the application performance when an optimal code tuning is applied.
5.1.3 Kernel performance with voltage frequency scaling (VFS)
Figure 12 shows the performance of seven reduction kernels with VFS on the three GPUs. For the first six kernels, the achieved performance is almost linearly proportional to the GPU core frequency. The reason is that in these kernels, the percentage of compute utilization is much higher than that of memory utilization that, which indicates that these kernels are compute- bound. Such compute-bound execution depends on the compute capability of the used GPU processing units, specifically GPU core frequency in this case. This “performance-frequency” characteristic is observed similarly for the first six kernels on all three GPUs.
The seventh kernel RK-7 has almost balance utilization percentage of GPU compute resource and memory resource. Therefore, kernel RK-7 has a different performance trend as GPU core frequency changes. The highest performance achieved in kernel RK-7 is found at 2000 MHz, 1100 MHz and 1100 MHz on GTX 560Ti, GTX 660 and GTX 970, respectively.
Figure 13 shows the achieved bandwidth of seven kernels on GTX 660 under various memory frequencies. The same trend is observed in other two GPUs. Unlike the GPU core frequency, the GPU memory frequency has very little impact on our application performance. This implies that scaling up a GPU memory frequency does not improve a compute-bound kernel performance.
5.2 Effect of optimization strategies on power and energy consumption
Because GTX 560Ti is not equipped with internal thermal sensor, it is not possible to measure GPU power consumption by the GPU-Z tool. Therefore, the analysis on power/energy consumption is done on two recent GPUs, GTX 660 and GTX 970. Figure 14 shows the GPU power consumption of seven reductions kernels with VFS.

Fig. 12 Performance of reduction kernels with GPU core VFS:
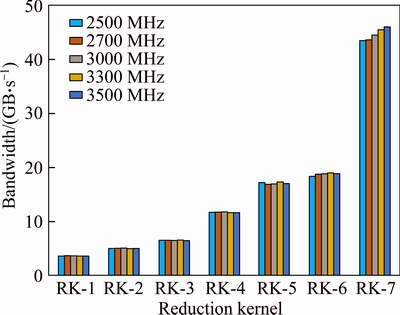
Fig. 13 Performance of reduction (on GTX 660) with GPU memory VFS
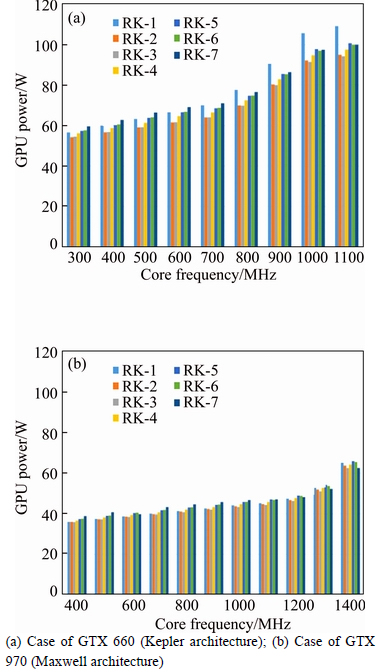
Fig. 14 Power consumption of reduction kernels with VFS:
The technique of avoiding warp divergent executions and reducing the number of inactive warps effectively reduces the GPU power consumption in kernel RK-2. This optimization reduces the power consumption by 9% on GTX 660 on average. It is clear that this technique does not only improve the performance but also the power consumption of a Kepler GPU. However, for Maxwell GTX 970, the power consumption is reduced only by 1%. It implies that for the same application, the optimization can affect GPU power differently according to target platform.
In RK-3 kernel, where the sequential addressing is used to avoid bank conflict, there is almost no change in power consumption in both GPUs. However, in “first add during load” RK-4 kernel, due to higher thread utilization by reducing inactive threads the power consumption is increased by 4% and 3% on GTX 660 and GTX 970, respectively.
Unrolling the last warp applied in RK-5 kernel increases the power consumption by 3% in both GPUs while completely unrolling technique applied in RK-6 does not make any change in GPU power consumption. Finally, the most optimized kernel RK-7 rises the power consumption only by 2% on GTX 660 and 1% on GTX 970 due to increase of memory utilization.
The energy consumption for all seven kernels is also evaluated to understand the trade-off between execution performance of a kernel and its power consumption. Due to the big improvement in performance and small increase in power consumption, the energy consumption is effectively reduced from one kernel to a more optimized kernel. Figure 15 shows the GPU energy consumption with varying core frequency. Compared to other kernels, the energy consumption has a bigger drop in RK-2, RK-4 and RK-7 kernels, where high performance gain is achieved accordingly. The optimum frequency where the lowest energy is consumed is found at each GPU’s default frequency.
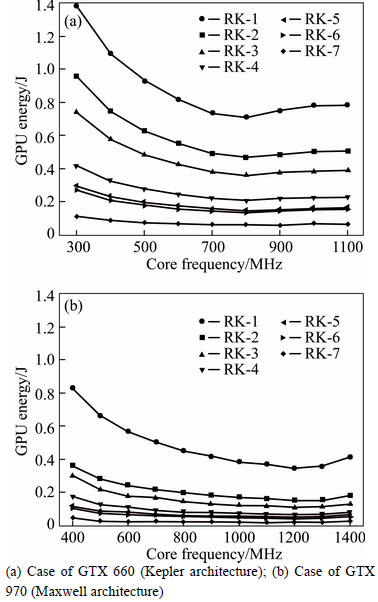
Fig. 15 GPU energy consumption of reduction kernels with VFS:
New Maxwell GPU architecture is designed to improve power and energy efficiency thanks to new improvements in “control partitioning”, “instruction scheduling”, “dependent arithmetic instruction latency reduction”, etc [25]. On average, GTX 970 is three times more energy efficient than GTX 660 Kepler architecture.
As memory frequency changes, the GPU power varies little. For GTX 560Ti, the average system power out of all kernels increases only by 2% when memory frequency increases from 1500 MHz to 2200 MHz. For GTX 660, the system power increases by 4% and GPU power increases by 6% when memory frequency increases from 2500 MHz to 3500 MHz. For the same range of memory frequency as GTX 660, the system power and GPU power of GTX 970 increase by 7% and 4%, respectively.
For all GPUs, memory frequency has more impact on power consumption of kernel RK-7 than that of other kernels. It can be explained that because RK-7 kernel has higher percentage of memory utilization (i.e., higher memory transactions and activities) than other kernels, it leads to higher power consumption on the memory. Specifically, when memory frequency increases from 2500 MHz to 3500 MHz, GPU power consumptions of RK-7 kernel in GTX 660 and GTX 970 increase by 9% and 10%, respectively.
Performance per watt (Gflops/W) is used to measure energy efficiency of each kernel. The techniques of reducing warp divergence, increasing thread utilization and balancing thread granularity and number of threads have a big effect on energy efficiency improvement. Specifically, on average these techniques improve the energy efficiency by 90%, 74% and 134%, respectively. While other optimizations such as avoiding bank-conflicts, unrolling the last warp and unrolling loop completely increase the performance per watt by 31%, 39% and 9%, respectively.
Table 5 shows the summary of optimization techniques and their performance, power and energy efficiency degree of impact. An optimization having a “High” impact means that optimization efficiently provides more than 50% improvement. A “Mid” impact indicates a 30%–50% improvement. Lastly, a “Low” impact means the optimization provides less than 30% improvement. Overall, it is seen that code optimization does not have a large impact on GPU power consumption as it does on performance and energy. Therefore, developers should apply various optimization strategies to the kernel code to achieve the best performance as possible.
Table 5 Optimization techniques and their impacts on performance, power and energy efficiency

6 Conclusions
To satisfy the increasing need for performance and constraints in power budget, many softwares as well as hardware optimizations have been proposed and applied. In this work, we have evaluated and analyzed GPU performance, power and energy consumption of application kernel codes with various optimization strategies on high performance desktop GPUs in order to investigate the impact of those optimization strategies on the GPU performance, power and energy.
Our results analysis shows that thread/warp execution efficiency (i.e. thread utilization and thread divergence) largely affects the application performance while bank conflict free and loop unrolling technique have a medium impact on it. Also, the proper choice of algorithm (i.e. cascading algorithm in this case) can produce an optimum code which can efficiently boost the performance up to several order. For the same application, different optimizations can affect GPU power differently according to the target platform. Overall, it is seen that code optimization has a larger impact on the application performance than on GPU power consumption. As a result, the energy consumption is effectively reduced from one kernel to a more optimized kernel. Measurement data achieved from VFS experiments show that the performance of a compute-bound kernel scales linearly with GPU core clock frequency while a higher memory-bound kernel does not follow the same trend. In addition, memory frequency does not have much impact on both application performance and GPU power.
Our work shows that the traditional well-known performance-oriented optimization strategies can improve significantly the overall energy efficiency with little increase of power consumption. We expect that our evaluation and analysis results can be further used as an optimization guideline for developing low power and low energy software accelerations on modern high-performance GPUs.
Acknowledgements
This work has been supported by Basic Science Research Program through the National Research Foundation (2015R1D1A3A01019869), Korea.
References
[1] STRATTON J A, ANSSARI N, RODRIGUES C, I J SUNG, OBEID N, CHANG L W, LIU G D, HWU W. Optimization and architecture effects on GPU computing workload performance [C]// Innovative Parallel Computing (InPar). San Jose, USA: IEEE, 2012: 1–10.
[2] RYOO S, RODRIGUES C I, BAGHSORKHI S S, STONE S S, KIRK D B, HWU W W. Optimization principles and application performance evaluation of a multithreaded GPU using CUDA [C]// Proceedings of the 13th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming (PPoPP '08). Utah, USA: ACM, 2008: 73–82.
[3] JANG B, DO S, PIEN H, KAELI D. Architecture-aware optimization targeting multithreaded stream computing [C]// Proceedings of 2nd Workshop on General Purpose Processing on Graphics Processing Units-GPGPU-2. Washington DC, USA: ACM, 2009: 62–70.
[4] JANG B, SCHAA D, MISTRY P, KAELI D. Exploiting memory access patterns to improve memory performance in data-parallel architectures [J]. IEEE Transactions on Parallel and Distributed Systems, 2011, 22(1): 105–118.
[5] MEI X, ZHAO K, LIU C, CHU X. Benchmarking the memory hierarchy of modern GPUs [M]. Heidelberg: Springer Berlin, 2014: 144–156.
[6] SUDA R, REN D. Accurate measurements and precise modeling of power dissipation of CUDA kernels toward power optimized high performance CPU-GPU computing [C]// The Tenth International Conference on Parallel and Distributed Computing, Applications and Technologies (PDCAT). Hiroshima, Japan: IEEE, 2009.
[7] CALANDRINI G 1, GARDEL A, BRAVO I, REVENGA P,  J L, TOLEDO-MOREO F J. Power measurement methods for energy efficient applications [J]. Sensors, 2013, 13(6): 7786– 7796.
J L, TOLEDO-MOREO F J. Power measurement methods for energy efficient applications [J]. Sensors, 2013, 13(6): 7786– 7796.
[8] DASGUPTA A, HONG S, KIM H, PARK J. A new temperature distribution measurement method on GPU architectures using thermocouples [R]. Georgia Institute of Technology, 2012.
[9] LANG J,  G. High-resolution power profiling of GPU functions using low-resolution measurement [C]// 19th International Conference on Parallel Processing (Euro-Par 2013). Aachen, Germany: Springer-Verlag Berlin, 2013: 801–812.
G. High-resolution power profiling of GPU functions using low-resolution measurement [C]// 19th International Conference on Parallel Processing (Euro-Par 2013). Aachen, Germany: Springer-Verlag Berlin, 2013: 801–812.
[10] COLLANGE S, DEFOUR D, TISSERAND A. Power consumption of GPUs from a software perspective [C]// ICCS '09 Proceedings of the 9th International Conference on Computational Science. LA, USA: Springer-Verlag Berlin, 2009: 914–923.
[11] PHUONG T Y, LEE J G. Software based ultrasound B-mode/beamforming optimization on GPU and its performance prediction [C]// 21th IEEE International Conference on High Performance Computing. Goa, India: IEEE, 2014: 1–10.
[12] JIAO Y, LIN H, BALAJI P, FENG W. Power and performance characterization of computational kernels on the GPU [C]// IEEE/ACM International Conference on Green Computing and Communications and International Conference on Cyber, Physical and Social Computing. Hangzhou, China: IEEE, 2010: 221–228.
[13] HONG S. Modeling performance and power for energy-efficient GPGPU computing [D]. Georgia: Georgia Institute of Technology, 2012.
[14] HONG S, KIM H. An analytical model for a GPU architecture with memory-level and thread-level parallelism awareness [J]. In ACM SIGARCH Computer Architecture News, 2009, 37: 152–163.
[15] HONG S, KIM H. An integrated GPU power and performance model [J]. In ACM SIGARCH Computer Architecture News, 2010, 38: 280–289.
[16] KASICHAYANULA K, TERPSTRA D, LUSZCZEK P, TOMOV S, MOORE S, PETERSON G D. Power aware computing on GPUs [C]// Symposium on Application Accelerators in High Performance Computing. Illinois, USA: IEEE, 2012: 64–73.
[17] ABE Y, SASAKI H, KATO S, INOUE K, EDAHIRO M, PERES M. Power and performance characterization and modeling of GPU- accelerated systems [C]// IEEE 28th International Symposium on Parallel and Distributed Processing. Arizona, USA: IEEE, 2014: 113–122.
[18] ABE Y, SASAKI H, PERES M, INOUE K, MURAKAMI K, KATO S. Power and performance analysis of GPU-accelerated systems [C]// Proceedings of the ACM Workshop on Power-Aware Computing and System. California, USA: ACM, 2012.
[19] MEI Xin-xin, YUNG Ling-sing, ZHAO Kai-yong, CHU Xiao-wen. A measurement study of GPU DVFS on energy conservation [C]// Proceedings of the ACM Workshop on Power-Aware Computing and System. Pennsylvania, USA: ACM, 2013.
[20] RONG G E. VOGT R, MAJUMDER J, ALAM A, BURTSCHER M, ZONG Zi-liang. Effects of dynamic voltage and frequency scaling on a K20 GPU [C]// Parallel Processing (ICPP), 2013 42nd International Conference. Lyon, France: IACC, 2013: 826–833.
[21] UKIDAVE Y, ZIABARI A K, MISTRY P, SCHIRNER G, KAELI D. Analyzing power efficiency of optimization techniques and algorithm design methods for applications on heterogeneous platforms [J]. International Journal of High Performance Computing Applications 2014, 28(3): 319–334.
[22] COPLIN J, BURTSCHER M. Effects of source-code optimizations on GPU performance and energy consumption [C]// Proceedings of the 8th Workshop on General Purpose Processing using GPUs. San Francisco, CA, USA, 2015.
[23] HARRIS M. Optimizing parallel reduction in CUDA, nvidia developer technology [EB/OL]. [2007]. http://developer.download. nvidia.com/compute/cuda/1.1-Beta/x86_website/projects/reduction/doc/reduction.pdf.
[24] NVIDIA [EB/OL]. [2017]. http://www.geforce.com/hardware/ desktop-gpus/geforce-gtx-titan-x/specifications.
[25] HARRIS M. 5 things you should know about the new maxwell GPU architecture [EB/OL]. [2014–02–21]. http://devblogs.nvidia. com/parallelforall/5-things-you-should-know-about-new-maxwell-gpu-architecture/
(Edited by YANG Hua)
Cite this article as: Phuong Thi Yen, Lee Deok-Young, Lee Jeong-Gun. Impacts of optimization strategies on performance, power/energy consumption of a GPU based parallel reduction [J]. Journal of Central South University, 2017, 24(11): 2624–2637. DOI:https://doi.org/10.1007/s11771-017-3676-5.
Received date: 2016-06-25; Accepted date: 2017-03-13
Corresponding author: Lee Jeong-Gun, PhD, Professor; Tel: +82–33–248–2312; E-mail: Jeonggun.Lee@hallym.ac.kr

