基于核理论均衡聚类和模糊支持向量机的
模拟电路诊断方法
唐静1 ,秦亮1 ,史贤俊2 ,肖支才 2
(1. 海军航空工程学院 研究生管理大队,山东 烟台,264001;
2. 海军航空工程学院 控制工程系,山东 烟台,264001)
摘要:核方法通过非线性映射将原始数据嵌入到高维特征空间,然后进行线性分析和处理,为基于知识的数据分析带来新的方法和模式。本文针对传统的K-均值聚类方法无法解决故障特征数据维数高、在故障样本交叠严重时多分类性能较差的问题。在电路故障特征数据预处理阶段,提出了一种类互均衡核K-均值法进行聚类,不仅克服了传统方法中分配不均或漏分问题,而且解决了特征数据维数高带来的奇异性问题,还有效提高了故障样本交叠时的多分类聚类性能;设计了一种核密度函数用于模糊支持向量机实现多故障的分类,给出了最优带宽的求解方法。将该方法应用于国际标准电路中的CTSV滤波器电路故障诊断中,结果表明:该方法能突出不同故障的特性,具有很高的故障识别率,具有广阔的工程应用前景。
关键词:核函数;K-均值聚类;模拟电路;故障诊断;模糊支持向量机
中图分类号:TP391 文献标志码:A 文章编号:1672-7207(2011)S1-0108-06
An analog circuit fault diagnosis method based on kernel K-means cluster method and FSVM
TANG Jing 1 , QIN Liang1 , SHI Xian-jun2 , XIAO Zhi-cai2
(1. Graduate Students’ Brigade, Naval Aeronautical and Astronautical University, Yantai 264001, China;
2. Department of Control Engineering, Naval Aeronautical and Astronautical University, Yantai 264001, China)
Abstract: A new methods and models for knowledge-based data analysis is brought by kernel method. It uses nonlinear mapping, the original data is embedded into a high dimensional feature space and linear analysis of the data and processing. Based on the fact that the traditional K-means clustering methods cannot solve the fault characteristics of the problem of high data dimension, and overlap in a serious fault samples, the method of classification performance is poor, in the circuit fault characteristic data pre-processing stage, the cross-equalization of nuclear cluster K-means method is presented, which not only overcomes the uneven distribution of the traditional method or the issue of data leakage points, but also solves the high dimensionality of feature data to bring the singularity, also effectively improves the fault samples overlapping clustering performance for the multi-classification. A kernel density function for fuzzy support vector machine is designed to achieve a classification of multiple faults. At the same time, the optimal method is given to solve the bandwidth. The method is applied in the circuit CTSV international standard filter circuit fault diagnosis, the results show that this method has higher recognition rate of failure, and has a good application prospect.
Key words: kernel function; K-means clustering method; analog circuit; fault diagnosis; fuzzy support vector machine
支持向量机的理论[1-2]快速发展,基于核的分析方法已被成功运用于解决许多现实世界的问题。核方法提供了通过某种非线性映射将原始数据嵌入到高维特征空间,然后利用线性学习方法在这个新空间中分析和处理的新模式,广泛应用在模式识别中的特征提取主成分分析、支持向量机分类等领域;在电路故障诊断方面,基于核理论的方法已成为研究的热点。尽管核方法能够表示目标间复杂的非线性关系,但核函数与核参数的选取对分类性能有着重要的影响。在理想情况下,可以依靠基于问题域的先验知识选择核函数,在已选核函数所定义的特征空间中将参数学习限制为某种具体的模式函数的选择[3-4]。但实际中,预先知道正确的核函数形式是十分困难的,同时,适用于任何数据的普遍存在的核函数也是不存在的,因此,需要找到一个对数据敏感的目标函数来估计核函数的性能。文献[5]提出了一种基于局部加权核Fisher准则的优化方法。首先利用核K-均值方法对数据进行子类划分,然后,根据各子类数据对之间的马氏距离求取距离最近的M对子类数据,最后利用加权的核优化判决准则对M对子类数据进行优化,获取最终的优化参数。该方法能够有效提高可分性较差的异类子类对间的距离,因此,对多子类数据呈现良好的分类性能。但该方法在计算子类对间的距离时采用马氏距离[6],当故障特征数据维数高时,奇异性问题导致马氏距离无法求取,而且该方法在用于故障分类时,对容差模拟电路导致的故障样本交叠及解决多分类问题时性能较差。针对这些问题,本文作者提出一种基于核理论的均衡聚类和支持向量机结合的容差模拟电路故障诊断方法。基本思路为:在电路故障特征数据预处理阶段,提出了一种类互均衡核K-均值法(Mutual cluster balanced K-means,简称MCBKM)进行聚类,不仅克服了传统核K-均值分类过程中易出现分配不均或漏分问题,而且解决了文献[5]中矩阵的奇异性问题;然后,针对MCBKM方法划分的各子类,利用核Fisher准则建立优化准则函数,利用梯度下降法实现核函数参数的优化;最后,设计了一种核密度函数用于模糊支持向量机实现多故障的分类。将该方法应用于ITC’97国际标准电路中的CTSV滤波器电路故障诊断中,结果表明,该方法能突出不同故障的特性并有效抵消含有野点和噪声的样本,具有很高的故障识别率。
1 核算法概述
核函数 是计算2个数据点在非线性变换
是计算2个数据点在非线性变换 下映像的内积,即
下映像的内积,即 。其中:
。其中: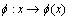 为核函数
为核函数 导出的特征变换;X为输入空间;
导出的特征变换;X为输入空间;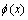 为特征空间;
为特征空间; 定义为某个Hilbert空间的内积,它首先应该是对称的,其次还要满足一些额外条件,即Mercer条件。
定义为某个Hilbert空间的内积,它首先应该是对称的,其次还要满足一些额外条件,即Mercer条件。
核算法的基本思想是将n维向量空间中的随机向量x利用非线性函数 映射到高维特征空间H,然后,在这个高维特征空间中设计线性的学习算法。如果其中各坐标分量间的相互作用仅限于内积,则无需知道
映射到高维特征空间H,然后,在这个高维特征空间中设计线性的学习算法。如果其中各坐标分量间的相互作用仅限于内积,则无需知道 的具体形式,只要利用满足Mercer定理的核函数替换线性算法中的内积,就可实现原空间中对应的非线性算法。
的具体形式,只要利用满足Mercer定理的核函数替换线性算法中的内积,就可实现原空间中对应的非线性算法。
2 类互均衡核K-均值聚类方法
传统的K-均值方法通过最小距离原则将相似样本聚集到相同聚类中[7]。由于K-均值方法是一种非监督学习方法,因此,无法保证聚类内各类样本数目的平衡,从而导致聚类结果易出现类别样本失衡的问题。为了解决这个问题,文献[8-11]提出了一种带监督的聚类学习方法――类内均衡K-均值法(Intra-cluster balanced K-means,简称ICBKM)。ICBKM方法适用于凸形状的样本数据,但对于非凸形状的数据,ICBKM的分类性能大大降低。为了提高聚类方法的通用性和有效性,同时为了满足核函数优化的需要,本文提出了一种新的聚类方法――类互均衡核K-均值法(Mutual cluster balanced K-means,简称MCBKM),即通过非线性映射,将数据映射到高维非线性空间,在非线性空间中完成样本的K-均值聚类,同时可以达到:聚类内各类样本的均衡,聚类间样本总数的均衡。
假设存在一组样本数据{(x1, z1), (x2, z2), …, (xN, zN)},其中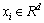 (i=1, …, N)是数据空间中第i个样本,zi(i=1, …, N)是第i个样本对应的类标信息,且
(i=1, …, N)是数据空间中第i个样本,zi(i=1, …, N)是第i个样本对应的类标信息,且 ,c为类别总数。另设第i个样本映射到特征空间F为
,c为类别总数。另设第i个样本映射到特征空间F为 ,则MCBKM在特征空间F的目标函数定义为式(1)。
,则MCBKM在特征空间F的目标函数定义为式(1)。

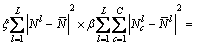

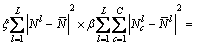
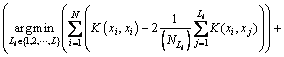

 (1)
(1)
式(1)中的第1部分类似于传统的核K-均值法,其最小化可以保证聚类收敛紧致。其中L表示聚类个数;Li表示F空间中第i个样本所属的聚类类标; 表示F空间中隶属于第Li个聚类中样本的均值;
表示F空间中隶属于第Li个聚类中样本的均值; 表示第
表示第 个聚类中的样本总数;
个聚类中的样本总数; 表示核函数。
表示核函数。
式(1)中的第2项反映各聚类间样本数的平衡程度和聚类内各类样本数的平衡程度。其中 表示第l个聚类中的样本总数;
表示第l个聚类中的样本总数; 表示样本数均值;
表示样本数均值; 表示第l个聚类中隶属第c类的样本数;
表示第l个聚类中隶属第c类的样本数; 表示第l个聚类内各类样本数的平均值。
表示第l个聚类内各类样本数的平均值。 和
和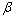 为加权系数;由此可知:只要满足D最小,每个样本
为加权系数;由此可知:只要满足D最小,每个样本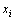 对应的聚类即为其所属聚类。
对应的聚类即为其所属聚类。
在MCBKM中,第2项是最关键的一步。为了保证聚类内、外样本数的平衡,对样本进行重新分配时,要先检查样本所属聚类内其他样本的类标信息,若其他样本的类标信息不少于2类,则根据新的聚类中心和距离原则将样本分配到L类中的某一类,否则保持样本的聚类类标不变。值得注意的一点是:对满足条件的样本进行聚类分配时,式(1)中第1项的变动会牵制第2项的变化,因此,最小化D并不是仅仅要求满足第1项最小化,而是一种全局动态聚类过程,这点有别于传统的核K-均值方法。
经过MCBKM处理后,数据根据其自身在特征空间中的分布,不同类别距离相近的样本聚集到一个聚类内,而距离相远的样本分配到不同的聚类,能对样本特征交叠的聚类方法进行有效的改进。由于式(1)的作用,避免了各聚类样本数据出现较大的差异,同时也避免了聚类内部某个类别的数据过多、其他数据过少情况的发生。
MCBKM算法的本质就是为了获取可分性较差的异类子类对,可以将可分性差的异类子类对直接聚集到一起,且子类对的个数与聚类个数相同,无需附加多余的门限判断。
3 核函数优化参数的建立
核函数的优化需要建立在一定的优化准则之上。经验特征空间中的类内-类间距离准则函数就是一种可行的方法。由于数据经MCBKM处理后,划分成多个异类子类对,因此,为了建立统一的优化目标函数,首先建立局部优化目标函数,根据局部优化目标函数来确定核函数的优化参数。
设经MCBKM处理后,第Li个聚类中的样本数据为 ,其中:
,其中: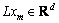 (m=1, 2, …, MLi,且MLi<N)为聚类中第m个样本,样本对应的类标为
(m=1, 2, …, MLi,且MLi<N)为聚类中第m个样本,样本对应的类标为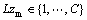 (m=1, 2, …, MLi)。基于数据的核函数定义为:
(m=1, 2, …, MLi)。基于数据的核函数定义为:
 (2)
(2)
其中: ;
; 为基本核函数,一般选用常用的高斯核函数、Poly核函数等。
为基本核函数,一般选用常用的高斯核函数、Poly核函数等。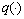 定义为:
定义为:
 (3)
(3)
 为联合系数,
为联合系数, ,
, 满足
满足 。定义对角线矩阵Q,其对角线上的元素为
。定义对角线矩阵Q,其对角线上的元素为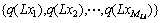 ,并记
,并记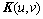 和
和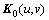 为
为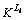 和
和 ,则:
,则:
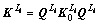 (4)
(4)
另设 ,
,
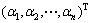 ,则
,则
 (5)
(5)
经验特征空间中核函数的可分性测度由类内-类间距离准则函数给出,由于可分性测度具有线性叠加性,且根据经验特征空间的定义,则局部优化目标函数可表示为:
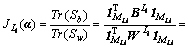
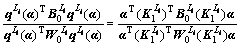 (6)
(6)
由此,将最大 对应的
对应的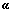 代入核函数(2)中,得到的核函数就能较合理反映经验特征空间中数据的分布结构。
代入核函数(2)中,得到的核函数就能较合理反映经验特征空间中数据的分布结构。
4 模糊支持向量机多分类器
采用模糊支持向量机对预处理的故障特征数据进行分类,相对常规支持向量机的训练样本,除了样本的特征与类属标识外,模糊支持向量机训练的每个样本还增加了模糊隶属度,这样可以有效减少噪声点和野点的影响。
设模糊支持向量机待诊断的训练样本集为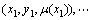 ,
,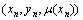 ,
, ,
, , 0<
, 0< ≤1。假设
≤1。假设 为将训练样本从原始空间RN映射到高维特征空间Z之间的映射关系。模糊隶属度
为将训练样本从原始空间RN映射到高维特征空间Z之间的映射关系。模糊隶属度 表示该样本隶属于某类的可靠程度,
表示该样本隶属于某类的可靠程度,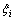 是支持向量机目标函数中的分类误差项,则
是支持向量机目标函数中的分类误差项,则 为带权误差项。得到的最优分类平面为下式目标函数的最优解。
为带权误差项。得到的最优分类平面为下式目标函数的最优解。
 (7)
(7)
式中:惩罚因子C为常数;w表示线性分类函数yi的权系数。由式(7)可以看出,当 很小时,也减小了
很小时,也减小了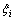 在式(7)中的影响,则可将xi看作不重要的样本。
在式(7)中的影响,则可将xi看作不重要的样本。
相应的最优分类面的判别函数为:
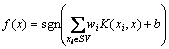 (8)
(8)
式中:K(xi, x)为核函数,本文采用高斯核。
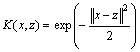 (9)
(9)
应用一种基于核密度估计方法简单有效的隶属度函数。
 (10)
(10)
 (11)
(11)
最优带宽为
 (12)
(12)
简单地说,理想的带宽为 ,然而,这个估计是在理想数据条件下取得的。实际上,带宽应该根据数据和密度估计的情况在一定范围内不断调整。
,然而,这个估计是在理想数据条件下取得的。实际上,带宽应该根据数据和密度估计的情况在一定范围内不断调整。
5 含容差模拟电路的多故障诊断实例
本文选择ITC’97国际标准电路中的CTSV滤波器为例进行仿真和分析。CTSV滤波器电路如图1所示。电路中电阻和电容等无源器件的容差设为10%。无源器件的标称值为R1= R2= R3= R4= R5=10 k?,R6=3 k?, R7=7 k?,C1= C2=20 nF。

图1 CTSV滤波器标准电路
Fig.1 Standard circuit CTSV filters
考虑待测电路的单一软故障,F1(R1+50%),F2(R1-50%),F3(C1+50%),F4(C1-50%),F5(C2+50%),F6(C2-50%),F7(R5+50%),F8(R5-50%),多种软故障组合为:F9(R1+50% & C 1+50%),F10(R 1-50% & C1-50%),F11(R5+50% & C2+50%),其中符号“+”或“-”表示故障值上偏或下偏离元件的标称值;加上电路正常工作状态NF,则共有12种状态模式。在NI-Multisim10电路仿真软件中对CTSV电路进行仿真,所有的故障模式均采用正态蒙特卡罗(Monte Carlo)分析,对电路每种故障模式进行150次Monte Carlo仿真。从Vin节点输入激励信号,激励信号采用脉宽为10 μs、幅度为5V的单脉冲信号作为电路的激励信号,在节点6(Output)处采集各种状态下电路的响应电压信号。对电路每次响应信号的前100 μs信号进行采样得1 000个数据点,进行5层Haar小波变换。由于小波变换理论中近似系数和细节系数分别体现了故障信号的低频和高频信息,本文用小波近似系数和细节系数构成模拟电路的2种故障特征,用每层近似系数的第1个数值构成低频特征,用每层细节系数的绝对值之和构成高频特征,分别构成五维低频和高频特征向量,并对其进行归一化处理。这样,电路每种状态模式的特征由150个低频特征和150个高频特征样本组成,其中50个样本用于训练,100个样本用于测试。
6 故障诊断步骤
(1) 首先根据电路故障特征提取所述的方法进行故障特征提取,每种故障经过上述计算可得到50个故障特征样本进行训练,形成一个50×10的矩阵。
(2) 求出各类样本中各自的中心c和最小超球半径r;
(3) 根据理想带宽求出每种模式节点6的核密度函数,根据核密度函数,得出各类故障数据的隶属度 ;
;
(4) 采用一对多的多分类策略将FSVM推广到多分类FSVM进行模拟电路的故障诊断。假如存在K个故障类别,则需要训练k个模糊支持向量机,对第k个模糊支持向量机,以第k类故障样本为正样本,其余类别为负样本,其样本z的模糊隶属度取值为:
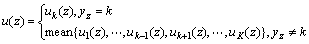 (13)
(13)
式中:yz表示样本z所属故障类标。
(5) 代入式(7)求解优化问题,获得第k个决策函数:
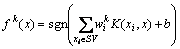 (14)
(14)
(6) 故障测试样本的故障类别。将测试样本点x代入前面求得的决策函数进行分类;
(7) 调整核密度函数的带宽hn和错分惩罚参数C,得到更加理想的故障诊断结果。
利用电路的故障特征数据对核优化方法的有效性进行验证。MCBKM参数L=2,ε=0.001,T=100,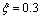 ,
, ,核函数选为高斯核函数。经过调整选取得核密度函数的带宽hn=5,错分惩罚参数C=12。表1给出不同方法下的诊断正确率。这里K&SVM表示利用传统的、未经优化的K均值聚类方法和支持向量机进行组合诊断;K&FSVM表示利用传统的、未经优化的K均值聚类方法和模糊支持向量机进行组合诊断;Ours表示利用优化的MCBKM技术和模糊支持向量机进行组合诊断。
,核函数选为高斯核函数。经过调整选取得核密度函数的带宽hn=5,错分惩罚参数C=12。表1给出不同方法下的诊断正确率。这里K&SVM表示利用传统的、未经优化的K均值聚类方法和支持向量机进行组合诊断;K&FSVM表示利用传统的、未经优化的K均值聚类方法和模糊支持向量机进行组合诊断;Ours表示利用优化的MCBKM技术和模糊支持向量机进行组合诊断。
表1 不同方法对应的诊断正确率
Table 1 Diagnosis results of different methods %

7 结论
本文提出的方法和故障诊断组合方法是一种可行的方法。从诊断性能上,本文所提出的优化组合诊断方法较传统的K&SVM和K&FSVM更适用于容差模拟电路的故障特征数据。并且对软多故障的诊断,本文所提出的方法性能最优,在保持精度的同时有效降低了故障特征数据的维数,具有很高的故障识别率。对该容差模拟电路的多故障诊断正确率达到94.49%,具有很好的诊断性能和广阔的工程应用前景。
参考文献:
[1] Vapnik V N. Statistical learning theory[M]. New York: Springer, 1995: 86.
[2] 王玗, 周志华, 周傲英. 机器学习及其应用[M]. 北京: 清华大学出版社, 2006: 315.
WANG Yu, ZHOU Zhi-hua, ZHOU Ao-ying. Machine learning and its application[M]. Beijing: Tsinghua University Press, 2006: 315.
[3] John S T, Cristianini N. 模式分析的核方法[M]. 赵玲玲, 等译. 北京: 机械工业出版社, 2006: 246.
John S T, Cristianini N. Kernel methods of pattern analysis[M]. ZHOU Ling-ling, et al, transl. Beijing: China Machine Press, 2006: 246.
[4] 陈渤, 刘宏伟, 保錚, 等. 一种针对雷达高分辨距离像的融合核优化算法[J]. 电子学报, 2006: 34(6): 1146-1151.
CHEN Bo, LIU Hong-wei, BAO Zheng, et al. Algorithm based on fusion kernel for high-resolution range profiles recognition[J]. Acta Electronic Sinica, 2006: 34(6): 1146-1151.
[5] Chen B, Liu H W, Bao Z. A kernel optimization method based on the localized kernel Fisher criterion[J]. Patterns Recognition, 2007: 41(3): 1098-1109.
[6] ZHANG Dao-qiang, CHEN Song-can, ZHOU Zhi-hua. Learning the kernel parameters in kernel minimum distance classifier[J]. Pattern Recognition, 2006, 39(1): 133-135.
[7] Xiong H L, Swamy M N S, Omair Ahmad M. Optimizing the kernel in the empirical feature space[J]. IEEE Trans Neural Networks, 2005, 16(2): 460-472.
[8] Sap M, Noor M. Weighted kernel K-means algorithm for clustering spatial data[J]. Journal Teknologi Maklumat, 2007: 16(2): 137-156.
[9] 杨健, 杨静宇, 王正群, 等. 一种组合特征抽取的新方法[J]. 计算机学报, 2002, 25(6): 570-575.
YANG Jian, YANG Jing-yu, WANG Zheng-qun, et al. A novel feature extraction method based on feature integration[J]. Chinese Journal of Computers, 2002, 25(6): 570-575.
[10] 季夜眉, 吴大贤. 概率论与数理统计[M]. 北京: 电子工业出版社, 2006: 167.
JI Ye-mei, WU Da-xian. Probability and mathematical statistics[M]. Beijing: Electronic Industry Press, 2006: 167.
[11] 张宝昌, 陈熙霖, 山世光, 等. 基于支持向量的Kernel判别分析[J]. 计算机学报, 2006, 29(12): 2143-2150.
ZHANG Bao-chang, CHEN Xi-lin, SHAN Shi-guang, et al. Kernel discriminant analysis based on support vectors[J]. Chinese Journal of Computers, 2006, 29(12): 2143-2150.
(编辑 陈灿华)
收稿日期:2011-04-15;修回日期:2011-06-15
基金项目:国家自然科学基金资助项目(61004002)
通信作者:唐静(1978-),男,湖北武汉人,博士研究生,工程师,从事智能电路故障诊断和测试技术;电话:0535-6635491;E-mail: tangj105@163.com