岩石临界应变能释放率测试及其相关规律

林杭^{1, 2}，李江腾¹，曹平¹

(1. 中南大学 资源与安全工程学院，湖南 长沙，410083；

2. 道路灾变防治及交通安全教育部工程研究中心，湖南 长沙，410004)

摘要：利用Instron1342型电液伺服材料试验机，采用双扭常位移松弛试验对矿石、大理岩、二辉橄榄岩、花岗岩4组岩石的试件进行断裂力学参数测试，获得相应的临界应变能释放率。以试验数据为依据，分析这4组岩石的临界应变能释放率与弹性模量及抗压强度的关系。研究结果表明：随着弹性模量或抗压强度的增加，临界应变能释放率也相应增大，且呈很好的线性关系；所建立的关系可为由抗压强度估算临界应变能释放率提供依据与帮助。

关键词：弹性模量；抗压强度；临界应变能；释放率

中图分类号：TV223.1          文献标志码：A         文章编号：1672-7207(2013)02-0714-04

Critical strain energy release rate test and its interrelated law of rock parameters

LIN Hang^{1, 2}, LI Jiangteng¹, CAO Ping¹

(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;

2. Engineering Research Center of Catastrophic Prophylaxis and Treatment of Road & Traffic Safety,Ministry of Education, Changsha 410004, China)

Abstract: Fracture mechanics parameters of ore, marble, lherzolite and granite were tested by double torsion constant displacement load relaxation method using Instron1342 type electro hydraulic servo test machine. Critical strain energy release rate was obtained. The relationship among critical strain energy release rate and elastic modulus, compression strength were studied according to testing results. The results show that critical strain energy release rate increases with the increase of elastic modulus E or compression strength σ_c. The curve of critical strain energy release rate-Young modulus (g_IC-E) and the curve of critical strain energy release rate-compression strength (g_IC-σ_c) accord with linear rules. The relations may provide a helpful method for estimating critical strain energy release rate from the compression strength or elastic modulus which can be measured more easily.

Key words: elastic modulus; compression strength; critical strain energy; release rate

岩体内部含有大量形状极不规则的孔隙、裂纹等内部缺陷，在载荷的进一步作用下，岩体内应力重新分布，其裂隙结构面不断演化、发展，累计损伤，使得岩体材料不断劣化，从而对岩石的强度、稳定性产生影响。岩石在受力直至失稳破坏的整个过程中，始终与外界进行能量交换，或将外部的能量转变为自身的内能，或将内部的应变能以一定的方式释放到外界，是能量驱动下的一种状态失稳现象。能量是物理反应的本质特征，是物质发生破坏的内在因素。在岩石破坏的整个过程中均存在能量的变化，可见，若能详细分析岩石变形破坏过程中的能量传递与转化，建立以能量变化为破坏判据，则有可能比较真实地反映岩石的破坏规律^[1]。Griffith^[2]利用能量方法提出了裂纹扩展准则，认为裂纹的虚拟扩展引起总势能的释放，当释放的能量与形成新断裂面所需的能量相同时，裂纹起裂。Palaniswamy^[3]提出了复合断裂的能量释放率准则，认为裂纹将沿着能产生最大能量释放率的方向扩展，当该方向上的能量释放率达到临界值时，裂纹开始扩展。而这些能量准则都需要确定材料应变能达到最大时的临界值，为此，Kumar等^[4-7]进行了大量的研究。然而，岩石的性质差别很大，其受力状态也各不相同，为此，本文作者对矿石、大理岩、二辉橄榄岩、花岗岩4组岩石进行断裂试验，得到4组岩石临界应变能释放率，并分析岩石的临界应变能释放率与弹性模量及抗压强度的关系。

1  断裂试验

1.1  基本原理

图1所示为试样示意图。其中：P为作用于扭杆上的荷载；试件为1个矩形薄板，在板的下表面沿长度方向的对称线开一中槽，使裂纹沿中槽扩展。假定试样未开裂部分为刚体, 已开裂部分忽略扭转以外所有的变形, 双扭试样可简化为1对长度等于试样裂纹长度a、截面为矩形的扭转棒^[8-11]。对于小变形y, 当扭转杆的宽度远大于试件的厚度时,扭转应变θ由下式给出^[12]：

            (1)

式中：y为加载点的位移；w_m为扭臂的长度；T为扭矩，； G为岩石的剪切模量；a为裂纹的长度。扭杆的宽度为w/2。

图1  双扭试件示意图

Fig.1  Schematic diagrams of double torsion specimen

将T的表达式代入式(1)，以柔度形式表示，有：

               (2)

式中：C为试件的柔度；d为试件的厚度。裂纹扩展的应变能释放率g与试件的柔度C有以下关系^[13-14]：

           (3)

式中：A 为裂纹的面积；d_n为裂纹面上试件的厚度。

将式(2)对 a求导，并将结果代入式(3)得：

                 (4)

又因为，故裂纹扩展的应变能释放率g为

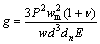              (5)

其中：E为弹性模量；ν为泊松比。当载荷P达到临界值P_C时，裂纹快速扩展，此时g也达到临界值g_IC：

            (6)

1.2  试验过程

将岩芯加工成图1所示的矩形薄片，各试样的尺寸与力学参数见表1^[15-17]。表2 所示为4组测试岩样的g_IC。

表1  试样尺寸与力学参数

Table 1  Specimens size and mechanical parameters

测试每个试样的破坏载荷P_c，利用式(6)可求得临界应变能释放率g_IC。图2所示为典型试件的载荷-时间曲线。

图2  典型试件K_IC实测载荷-时间曲线

Fig.2  Load-time curve of typical specimen in testing K_IC

表2  测试试样临界应变能释放率g_IC

Table 2  Critical strain energy release rate g_IC of tested sample      N/m

2  临界应变能释放率相关规律

从理论上说，抗压强度越高，其抵抗裂纹扩展的能力增强，即临界应变能释放率越大。4组岩石的弹性模量E、抗压强度σ和临界应变能释放率g_IC如表3所示；岩石临界应变能释放率与弹性模量及抗压强度的变化关系分别如图3和图4所示。从表3、图3和图4可以看出：临界应变能释放率随弹性模量或抗压强度的增加而增加，理论结果与实验结果相一致。

表3  岩石临界裂纹释放率g_IC、弹性模量E和抗压强度σ

Table 3  Fracture toughness and compression strength of rock

图3  临界应变能释放率g_IC随弹性模量E的变化关系

Fig.3  Relationship between critical strain energy release rate g_Ic and elastic modulus E

图4  临界应变能释放率g_IC随抗压强度σ_C变化关系

Fig.4  Relationship between critical strain energy release rate g_IC and compression strength σ_C

采用如下线性方程对临界应变能释放率g_IC与弹性模量E关系进行拟合：

g_IC=4.069 5E+13.557           (7)

得到拟合相关系数为R=0.924，说明二者关系具有较好的线性特征。

采用如下线性方程对临界应变能释放率g_IC与抗压强度σ_c的关系进行拟合：

g_IC=1.94σ_c-55.377            (8)

得到拟合相关系数为R=0.854，说明二者关系具有较好的线性特征。

3  结论

(1) 利用Instron1342型电液伺服材料试验机，采用双扭常位移松弛试验对矿石、大理岩、二辉橄榄岩、花岗岩4组岩石的临界应变能释放率进行了试验研究，分析了临界应变能释放率与弹性模量及抗压强度之间的关系。

(2) 临界应变能释放率g_IC随着弹性模量E的增加而增加，且有很好的线性关系，其关系为：g_IC=4.069 5E+13.557，相关系数R=0.924。

(3) 随着抗压强度σ_c的增加，岩石的临界应变能释放率g_IC也增大，也有比较好的线性关系。其关系为：g_IC=1.946 0σ_c-55.377，相关系数R=0.854。

(4) 由于弹性模量或抗压强度测试方法简单，而临界应变能释放率测试方法较复杂，所建立的关系为由弹性模量或抗压强度估算临界应变能释放率提供依据与帮助。

参考文献：

[1] 谢和平, 彭瑞东, 鞠扬, 等. 岩石破坏的能量分析初探[J]. 岩石力学与工程学报, 2005, 24(15): 2603-2608.

XIE Heping, PENG Ruidong, JU Yang, et al. On energy analysis of rock failure[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(15): 2603-2608.

[2] Griffith A A. Phenomena of rupture and flow in solid[J]. Philos Trans R Soc London Ser, 1920, 221(A): 163-198.

[3] Palaniswamy K, Knauss W G. Mechanics today[M]. New York: Pergamen, 1976: 78-92.

[4] Kumar A M, Sorensen B F. Fracture energy and crack growth in surface treated Yttria stabilized zirconia for SOFC applications[J]. Materials Science and Engineering A, 2002, 333(2): 380-389.

[5] Qiuhua R R. Shear frccture(mode II) of brittle rock[J]. International Journal of Rock Mechanics & Mining Sciences, 2003, 40(3): 355-375.

[6] 阎俊霞, 王立君, 徐凯龄. 纯弯曲Sandwich梁试样界面裂纹扩展的应变能释放率[J]. 复合材料学报, 1999, 16(1): 72-76.

YAN Junxia,WANG Lijun,XU Kailing. Strain energy release rate of crack propagation along the pure bend sandwich beam specimen[J]. Acta Materiae Compositae Sinica, 1999, 16(1): 72-76.

[7] 李洪升, 王悦东, 刘维波. 冻土非线性临界应变能释放率的测试方法[J]. 铁道科学与工程学报, 2007, 4(1): 53-57.

LI Hongsheng, WANG Yuedong, LIU Weibo. Measured method of nonlinearity critical strain energy release rate of frozen soil[J]. Journal of Railway Science and Engineering, 2007, 4(1): 53-57.

[8] 鲁国富, 刘勇, 张呈林. 基于虚拟裂纹闭合技术的应变能释放率分析[J]. 复合材料学报, 2009, 26(2): 210-217.

LU Guofu, LIU Yong, ZHANG Chenglin. Analysis of strain energy release rate based on virtual crack closure technique[J]. Act a Materiae Compositae Sinica, 2009, 26(2): 210-217.

[9] Ebrahimi M E, Chevalier J, Fantozzi G. Slow crack growth behavior of alumina ceramics[J]. Journal of Materials Research, 2000, 15(1): 142-147.

[10] Andreas K, Eckhard P, Jorg W, et al. Subcritical crack growth in Al₂O₃ with submicron grain size[J]. Journal of the European Ceramic Society, 2003, 23(1): 81-89.

[11] Ciccotti M, Gonzato G, Mulargia F. The double torsion loading configuration for fracture propagation: An improved methodology for the load-relaxation at constant displacement[J]. International Journal of Rock Mechanics & Mining Sciences, 2000, 37(7): 1103-1113.

[12] Ciccotti M, Negri N, Gonzato G, et al. Practical application of an improved methodology for the double torsion load relaxation method[J]. International Journal of Rock Mechanics & Mining Sciences, 2001, 38(4): 569-576.

[13] 范钦珊, 殷雅俊. 材料力学[M]. 北京: 清华大学出版社, 2012: 25-47.

FAN Qinshan, YIN Yajun. Material mechanics[M]. Beijing: Tsinghua University Press, 2008: 25-47.

[14] 张晓敏. 断裂力学[M]. 北京: 清华大学出版社, 2012: 45-80.

ZHANG Xiaomin. Fracture mechanics[M]. Beijing: Tsinghua University Press, 2012: 45-80.

[15] 张楚汉, 金峰. 岩石和混凝土离散—接触—断裂分析[M]. 北京: 清华大学出版社, 2008: 34-51.

ZHANG Chuhan, JIN Feng. Rock and concrete discrete—contact—fracture analysis[M]. Beijing: Tsinghua University Press, 2008: 34-51.

[16] 李江腾. 硬岩矿柱失稳及时间相依性研究[D]. 长沙:中南大学资源与安全工程学院, 2005: 30-48.

LI jiangteng. Study on instability and time dependence of pillar in hard rock mass[D]. Changsha: Central South University. School of Resources and Safety Engineering, 2005: 30-48.

[17] CAO Ping, LI Jiangteng, YUAN Haiping. Testing study of subcritical crack growth and fracture toughness in different rocks[J]. Transactions of Nonferrous Metals Society of China, 2006, 16(3): 709-713.

(编辑  陈灿华)

收稿日期：2012-02-22；修回日期：2012-04-26

基金项目：湖南省自然科学基金资助项目(11JJ4043)；高等学校博士学科点专项科研基金资助项目(20120162120014)；长沙理工大学道路灾变防治及交通安全教育部工程中心开放基金资助项目(KFJ100306)

通信作者：林杭(1980-)，男，福建福州人，博士，讲师，从事岩土工程理论和数值计算研究；电话：13787016941；E-mail：linhangabc@126.com