Field synergy analysis of different flow patterns in falling-film dehumidification system with horizontal pipes
来源期刊:中南大学学报(英文版)2020年第8期
论文作者:牛润萍 匡大庆 王世政 陈潇义
文章页码:2353 - 2366
Key words:film falling between horizontal pipes; fluent software; flow pattern of liquid film; synergy angle; mass and heat transfer
Abstract: Effects of the flow pattern of intertubular liquid film on mass and heat transfer synergies in a falling-film dehumidification system with horizontal pipes are studied. A flow model of the dehumidifying solution between horizontal pipes is established using Fluent software, the rule of transitions of the flow pattern between pipes is studied, critical Reynolds numbers of flow pattern transitions are obtained, and the accuracy of the model is verified by experiments. The mass transfer synergy angle and heat transfer synergy angle are respectively used as evaluation criteria for the mass transfer synergy and heat transfer synergy, and distribution laws of the synergy angles for droplet, droplet columnar and curtain flow patterns are obtained. Simulation results show that the mass transfer synergy angles corresponding to droplet, droplet columnar and curtain flow patterns all rise to a plateau with time. The mean mass-transfer synergy angle is 98° for the droplet flow pattern, higher than 96.5° for the droplet columnar flow pattern and 95° for the curtain flow pattern. The results show that the mass transfer synergy of the droplet flow pattern is better than that of the droplet columnar flow pattern and that of the curtain flow pattern.
Cite this article as: NIU Run-ping, KUANG Da-qing, WANG Shi-zheng, CHEN Xiao-yi. Field synergy analysis of different flow patterns in falling-film dehumidification system with horizontal pipes [J]. Journal of Central South University, 2020, 27(8): 2353-2366. DOI: https://doi.org/10.1007/s11771-020-4454-3.

J. Cent. South Univ. (2020) 27: 2353-2366
DOI: https://doi.org/10.1007/s11771-020-4454-3

NIU Run-ping(牛润萍), KUANG Da-qing(匡大庆), WANG Shi-zheng(王世政), CHEN Xiao-yi(陈潇义)
Beijing Engineering Research Center of Sustainable Energy and Buildings,
Beijing University of Civil Engineering and Architecture, Beijing 100044, China
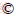 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract: Effects of the flow pattern of intertubular liquid film on mass and heat transfer synergies in a falling-film dehumidification system with horizontal pipes are studied. A flow model of the dehumidifying solution between horizontal pipes is established using Fluent software, the rule of transitions of the flow pattern between pipes is studied, critical Reynolds numbers of flow pattern transitions are obtained, and the accuracy of the model is verified by experiments. The mass transfer synergy angle and heat transfer synergy angle are respectively used as evaluation criteria for the mass transfer synergy and heat transfer synergy, and distribution laws of the synergy angles for droplet, droplet columnar and curtain flow patterns are obtained. Simulation results show that the mass transfer synergy angles corresponding to droplet, droplet columnar and curtain flow patterns all rise to a plateau with time. The mean mass-transfer synergy angle is 98° for the droplet flow pattern, higher than 96.5° for the droplet columnar flow pattern and 95° for the curtain flow pattern. The results show that the mass transfer synergy of the droplet flow pattern is better than that of the droplet columnar flow pattern and that of the curtain flow pattern.
Key words: film falling between horizontal pipes; fluent software; flow pattern of liquid film; synergy angle; mass and heat transfer
Cite this article as: NIU Run-ping, KUANG Da-qing, WANG Shi-zheng, CHEN Xiao-yi. Field synergy analysis of different flow patterns in falling-film dehumidification system with horizontal pipes [J]. Journal of Central South University, 2020, 27(8): 2353-2366. DOI: https://doi.org/10.1007/s11771-020-4454-3.
1 Introduction
Liquid desiccant dehumidification is a new technology developed in the field of air conditioning in recent years. Compared with traditional compression refrigeration dehumidification technology, it has obvious characteristics of energy saving and high efficiency. Many scholars have studied liquid desiccant dehumidification systems, especially systems that adopt falling-film dehumidification between horizontal pipes. ZENG et al [1] studied the liquid desiccant dehumidification system based on condensation heat regeneration. The results show that the flow rate and temperature of air and solution have positive effect on the regeneration rate. Under typical working conditions in summer, when the solution concentration is 21.20%-24.91%, the condensing heat utilization rate fluctuates from 0.416 to 0.507, and reducing the solution concentration is conducive to improving the condensing heat utilization rate. QI et al [2] proposed a new set of mass transfer correlations for the film instability in the process of falling film dehumidification, and this set of correlation equations takes into account the influence of flow dynamics, marangoni effect and other factors, as well as the influence of liquid and air contact conditions on the interface characteristics and wettability. LIU et al [3] found that the number of mass transfer units and heat capacity ratio were two important factors affecting the mass transfer performance of liquid desiccant dehumidification systems. WANG et al [4] established a new type of liquid desiccant dehumidification system by introducing ultrasonic atomization technology and found that the reaction area of the new system was tens to hundreds of times that of the traditional filler dehumidifier, which could reduce the amount of dehumidifier required and energy consumption. NAIK et al [5] studied the effect of air humidity ratio on the performance of liquid desiccant dehumidification system. They established a two-dimensional model to study the performance of dehumidifier and regenerator in an adiabatic countercurrent liquid dehumidification system. The optimal intake conditions of dehumidifier and regenerator are obtained within the given operating parameters. OU et al [6] proposed an energy-saving liquid desiccant dehumidification system and established a model to study the mass and heat transfer performance of the system. The effects of key parameters on the performance of the system and the feasibility of reducing the dilution and energy consumption of the solution were studied. Results showed that compared with results for a traditional solution, the dilution rate of the solution was below 39.64% and the energy consumption was below 22.3%. At present, most analysis of laws of mass transfer in the dehumidification process involves establishing mass transfer expressions using macroscopic parameters. There is still much space to study other microscopic and local laws involved in the process of dehumidification. Falling-film flow is a low-speed open flow that has attracted much attention owing to its complex dynamic behavior and non-linear characteristics. WANG et al [7] conducted an experimental study on falling-film flow and obtained the Reynolds numbers and deviation values of four membrane state transitions in different pipes. YANG et al [8] numerically simulated the falling-film flow of refrigerant outside a pipe and analyzed the effects of different factors on the flow of refrigerant outside the pipe. HOU et al [9] studied the flow field and temperature field on the shell side of a horizontal-pipe falling-film evaporator, obtained the distribution of thermodynamic parameters inside the evaporator and analyzed changes in the flow field, temperature field and other main parameters on the shell side. ROGERS et al [10] solved the energy equation and motion equation of falling-film flow in horizontal-pipe laminar flow. CHINNOV et al [11] studied the fluctuation of the Marangoni effect in falling-film flow. DONG et al [12] studied the effect of surface characteristics of a falling film dehumidifier on dehumidification performance. They proposed surface free energy to study the effect of surface characteristics on system performance. The results show that the system energy consumption can be reduced by 9.6% by improving the surface wettability of the dehumidifier. JIGE et al [13] studied the falling film flow of two refrigerants, R1234ze (E) and R245fa, in smooth horizontal tubes, and observed the flow rules of falling liquid film between tubes under adiabatic and heating conditions, and obtained the influence rules of Reynolds number, saturation temperature and heat flux on heat transfer. Most scholars have only studied the solution characteristics, equipment structure, dehumidification performance, matching of the macroscopic operating parameters of the solution but not studied the liquid desiccant, and so on, dehumidification from a microscopic perspective. In a system of falling-film dehumidification between horizontal pipes, the flow pattern of the solution has an important effect on the heat and mass transfer performances of the system. However, few scholars have studied the flow pattern of the solution. Intertubular flow patterns of the solution can be divided into droplet, droplet columnar and curtain flow patterns, and different intertubular flow patterns have different effects on the performance of the system. The flow pattern of the solution can be studied from the microscopic perspective of the liquid desiccant dehumidification system, so as to fill gaps in the literature.
The theory of field synergy, a new theory, is widely used in the field of single-phase heat transfer and studied by many scholars. ZENG et al [14] summarized the effects of triangular and rectangular wingtips and the flow velocity on the synergy angle, and concluded that enhanced heat transfer of the longitudinal vortex generator is due to improved synergy between the flow field and temperature field. WU et al [15] simulated the flow field of two different valves. The velocity distribution, the pressure drop, the cosine distribution of synergy was obtained. By comparing the velocity distribution and the cosine distribution of the synergy angle of the local flow field, the mechanism of the change of the flow resistance was revealed. Two methods for optimizing valve design are proposed based on the theory of field synergy. ZHONG et al [16] adopted the viewpoint of field synergy to overcome the shortcomings of traditional analysis methods, thus combining the pulsating- flow heat transfer mechanism and field synergy theory. LI et al [17] used the theory of field synergy to optimize the flow of a microchannel and concluded that Nusselt number and field synergy angle can be used to evaluate the heat transfer effect. The theory of field synergy has a broad generalization for traditional heat transfer technology and is of great significance for the optimization of heat transfer. However, few scholars have applied the theory of field synergy to the mass transfer field, and even fewer have applied the theory of field synergy to the dehumidification field.
In this study, the theory of field synergy was applied to studying the falling-film dehumidification process between two pipes. The simulation model of the system was established by Fluent software. By changing the flow rate of the lithium chloride solution, the flow patterns between different pipes were obtained, and the critical Reynolds number of the flow state transition between pipes was obtained. The simulation results were verified by experiment. By introducing the synergy angle through field synergy theory, the synergy angle distribution of different flow states between pipes was simulated, and the mass transfer synergy of different flow states was analyzed.
2 Model establishment
2.1 Physical model
The physical model of the dehumidifier established in Figure 1 is used to study the effect of the liquid distribution between pipes on dehumidification synergy. The equipment has dimensions of 80 mm×40 mm. The diameter of a horizontal pipe is 16 mm while the spacing of horizontal pipes is 30 mm. The diameter of the distribution mouth of the lithium chloride solution is 4 mm. The dehumidification solution inlet is located on the upper part of the horizontal pipe, and the wet air inlet is on both sides of the bottom of the model. Wet air flows from the bottom up to exchange heat and mass with lithium chloride solution flowing from the top down. Fluent simulation software is used to study the effect of the fluid flow pattern between the horizontal pipes on the mass transfer synergy in wet air. Using the synergy angle as the evaluation index, the distributions of the synergy angle under droplet, droplet columnar and curtain flow patterns are compared. When the liquid film has a curtain flow pattern, different liquid film flow patterns can be obtained by changing the velocity of the desiccant solution.
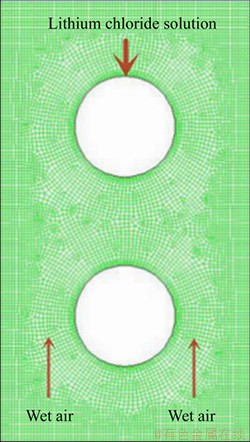
Figure 1 Physical model of dehumidifier
2.2 Mesh generation and step size setting
Gambit software is used to create an unstructured mesh automatically. The number of cells is selected as 2×103 and the mesh is locally encrypted at the pipe wall. The simulation step size is set at 0.001 to ensure fast convergence of the iterative calculation.
In this paper, the above model was divided into meshes for several times, and the simulation comparison is made for each case. As shown in Figure 2, based on the moisture content of air, it can be known that the change becomes stable at 2×103. The greater the number of meshes, the higher the accuracy, but the longer the time. Therefore, the mesh corresponding to 2×103 was selected for simulation.
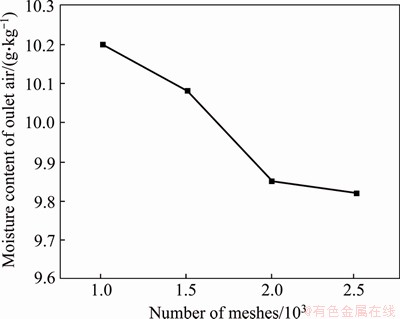
Figure 2 Independent verification
2.3 Mathematical model
Fluent software can be used to simulate the dehumidification process of falling film between pipes. As shown in Figure 1, the dehumidifying solution flows vertically downward, and the following four assumptions need to be made before solving.
1) The liquid concentration is the same in the horizontal direction, but the vertical direction is linear variation.
2) The liquid is simplified to a Newtonian fluid.
3) The inlet flow of liquid and air is uniform.
4) The system does not dissipate heat from the outside.
2.3.1 Governing equations
1) Volume-of-fluid model
The volume-of-fluid model is used to track the phase interface by solving the volume ratio equation for a single phase or multiple phases. For q phase, the equation is:
 (1)
(1)
where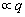 is the volume fraction of q phase.
is the volume fraction of q phase.
2) The momentum conservation equation is:
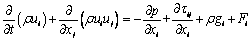 (2)
(2)
where Fi is related source items; τij is the stress tensor; and p is the fluid pressure.
3) The mass conservation equation is:
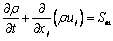 (3)
(3)
where Sm is custom source term.
4) The energy conservation equation is:
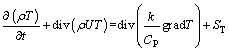 (4)
(4)
where cp is the specific heat capacity of the fluid, J/(kg·K); T is the fluid temperature, K; k is the heat transfer coefficient, W/(m2·K); ST is the internal heat source of the fluid;
5) The component transport equation is:
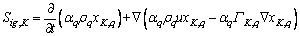 (5)
(5)
where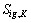 is the quality source at the interface, kg/m3; xK,q is the mass fraction of component
is the quality source at the interface, kg/m3; xK,q is the mass fraction of component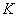 in the
in the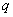 phase; ΓK,q is the diffusion coefficient of component
phase; ΓK,q is the diffusion coefficient of component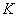 in the
in the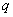 phase, m2/s.
phase, m2/s.
2.3.2 Settings of boundary conditions
1) The parameters of the dehumidifying solution at the entrance are:
X=0, T=Tl,in, c=cl,in, v=vl,In
where Tl,in is the temperature of inlet solution, K; cl,in is specific heat capacity of inlet solution,J/(kg·K); vl,in is the velocity of the inlet solution, m/s.
2) The parameters of wet air at the inlet are:
X=L, T=Tair,in, c=cair,in, v=vair,in
where Tair,in is the temperature of inlet air, K; cair,in is specific heat capacity of inlet air, J/(kg·K); vair,in is the velocity of the inlet air, m/s.
3) The mass transfer flux at the interface between wet air and dehumidifying solution is:
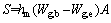 (6)
(6)
where hm is the convective mass transfer coefficient, m/s; Wg,b is the air-side moisture content, g/kg; Wg,e is the solution-side equivalent moisture content, g/kg.
3 Simulation and model verification of flow pattern between pipes
3.1 Analysis of flow pattern
The solution flows between the two pipes, forming a variety of flow patterns. Different flow patterns have different effects on heat and mass transfer. Droplet, droplet columnar and curtain flow patterns are selected for investigation in simulating flow under certain conditions. During the falling process, the liquid film can be divided into five zones, namely a freefall area, impact area, development area, full-development area and wake area [18].
3.1.1 Curtain and droplet columnar flow patterns
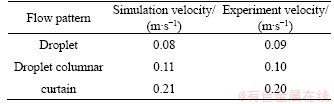
The inlet velocity, temperature and concentration of lithium chloride solution were 0.21 m/s, 27.5 °C and 0.3, respectively, and the inlet temperature, moisture content and velocity of wet air were 33 °C, 20 g/kg and 0.1, respectively. Different flow patterns are formed by changing the velocity of the lithium chloride solution. The velocities that produce the droplet, droplet columnar and curtain flow patterns are respectively 0.21, 0.11 and 0.08 m/s.
Figures 3(a) and (b) show the membrane state distribution for the curtain flow pattern at 0.5 and 0.7 s, respectively, while Figures 4(a) and (b) show the membrane state distribution of the drop columnar flow pattern at 0.5 and 0.8 s, respectively. As the flow of air becomes less stable, the flow direction of the liquid film between the pipes deviates from being vertically downward. It is found that the liquid film in the curtain flow pattern is relatively stable and has good wettability against the pipe wall, and the liquid film wraps around the pipe wall evenly in this case. The droplet columnar flow pattern is intermittent and has poor wettability against the wall and some dry areas.
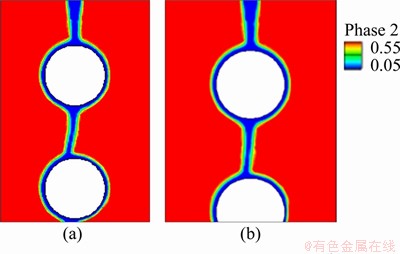
Figure 3 Curtain flow pattern at 0.5 s (a) and 0.7 s (b)
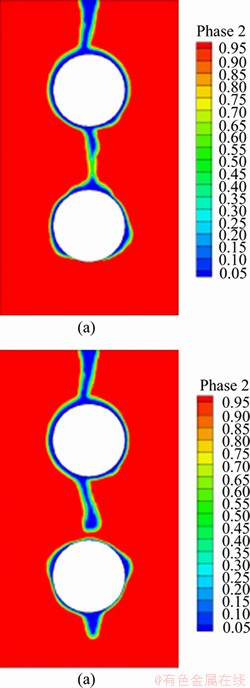
Figure 4 Droplet columnar flow pattern at 0.5 s (a) and 0.8 s (b)
3.1.2 Droplet flow pattern
There is a droplet flow pattern between pipes when the inlet velocity of lithium chloride solution is 0.08 m/s. The counter-flow dehumidification simulation results for the droplet flow pattern are shown in Figure 4.
Figures 5(a)-(f) show the recorded falling, stretching and breaking process of the solution in the case of the droplet flow pattern between the two pipes. The solution quickly accumulates on the top of the upper horizontal pipe after dropping from above. Under the action of gravity, the liquid film on the top of the upper horizontal pipe begins to thin and moves towards the two sides of the upper horizontal pipe, eventually converging at the bottom of the pipe. As time passes, the liquid film at the top and both sides of the upper horizontal pipe becomes thinner while the liquid film at the bottom of the pipe becomes thicker. Owing to the continuous concentration of the solution, under the continuous action of gravity, the liquid film at the bottom of the upper horizontal pipe begins to break away and flow to the lower horizontal pipe. The space in which the droplet flow pattern can grow is large, and there are thus liquid drops that are completely separated from the upper and lower pipes. The flow process continues such that there is a continuous flow of droplets. The enveloping property of the droplet flow pattern is poor, and there is a large dry area on the pipe wall.
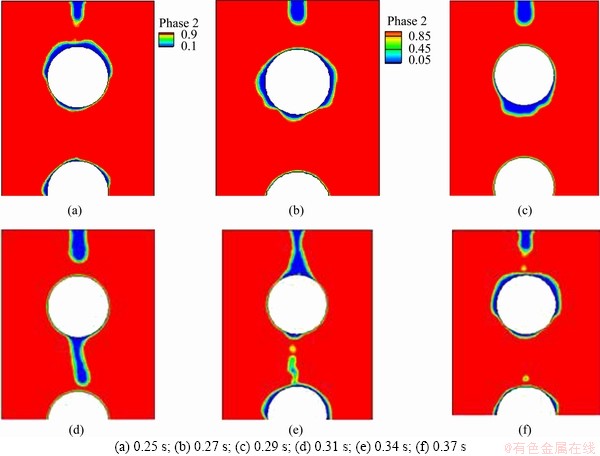
Figure 5 Droplet flow pattern at different times:
3.2 Critical Reynolds numbers of flow pattern transition
If the dehumidification solution and the wet air are both incompressible fluids, the Reynolds number is expressed as Re=4Г/μ, where Г is the solution mass flow rate per unit length for one side of the pipes and μ is the kinetic viscosity of the solution. Different flow patterns are obtained by adjusting the flow velocity of the dehumidification solution. Figures 6(a)-(c) show the intertubular flow patterns of lithium chloride solutions at different Reynolds numbers. Critical Reynolds numbers Re are obtained by multiple velocity regulation; that is, there are droplet, droplet columnar and curtain flow patterns between the pipes when Re≤45, 45<RE≤60 and 91<Re≤140, respectively.
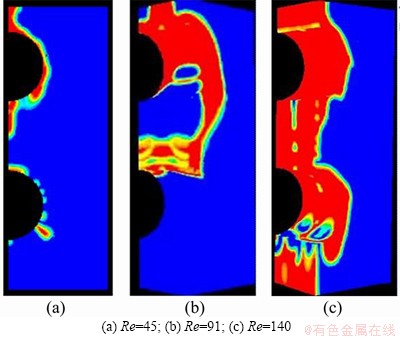
Figure 6 Transitions of flow pattern at different times:
3.3 Verification of model
We constructed a falling-film dehumidification experiment platform, which was set up to match the simulation, to verify the accuracy of the established model. Copper pipes with a diameter of 16 mm were selected. The spacing between horizontal pipes was set at 30 mm, and the diameter of the solution distribution mouth was set at 4 mm. The lithium chloride solution at the inlet had a temperature of 27.5 °C and a concentration of 0.3. The wet air at the inlet had a temperature of 33 °C, a moisture content of 20 g/kg and a velocity of 0.10 m/s. The flow pattern of the liquid film between pipes was observed while adjusting the flow velocity of the solution. Simulation and experimental results are compared in Figures 7-9. The flow rate settings of the simulation and experiment are given in Table 1. For nearly the same flow rates, the flow patterns between the pipes observed in simulation and experiment are consistent, which verifies the accuracy of the model.
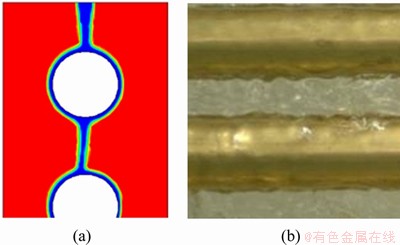
Figure 7 Comparison of curtain flow in simulation (a) and experiment (b)
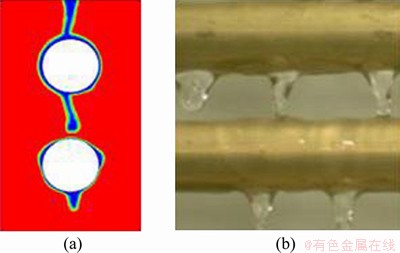
Figure 8 Comparison of droplet columnar flow in simulation (a) and experiment (b)
4 Field synergy analysis under different flow patterns
4.1 Theory of field synergy
The differential equation for a two- dimensional steady state with respect to mass transfer is:
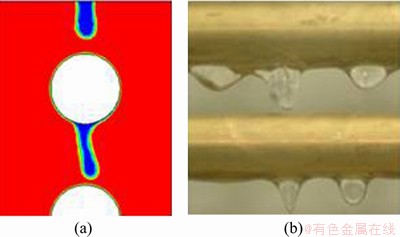
Figure 9 Comparison of droplet flow in simulation (a) and experiment (b)
Table 1 Comparison of flow velocities observed in simulation and experiment
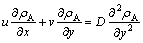 (7)
(7)
where 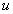 is the velocity of the fluid in the
is the velocity of the fluid in the 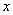 direction, m/s;
direction, m/s; 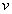 is the velocity of the fluid in the
is the velocity of the fluid in the 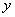 direction, m/s;
direction, m/s; 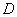 is the diffusion coefficient, m2/s.
is the diffusion coefficient, m2/s.
The integral from 0 to δc in the concentration boundary layer is written in vector form:
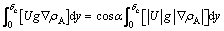 (8)
(8)
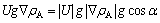 (9)
(9)
According to Eq. (10), when the modulus of the velocity vector and concentration gradient vector remain unchanged, a larger value of cos α leads to a larger-quantity product and a stronger mass transfer effect in the dehumidification process.
4.1.1 Calculation of synergy angle
The Tecplot software is used to calculate the synergy angle. It is obtained by taking known physical quantities in Tecplot and substituting them into the equation:
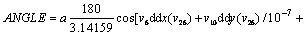
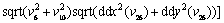 (10)
(10)
where v6 is the horizontal component of the velocity; v10 is the vertical component of the velocity; and v26 is the moisture content of wet air.
4.1.2 Arithmetic mean synergy angle
After the simulation has run to a certain extent, the synergy angle stabilizes and fluctuates around a certain value, as shown in Figure 10. The perform integration function of Tecplot is used to calculate the mean value for many stable states as the arithmetic mean synergy angle.
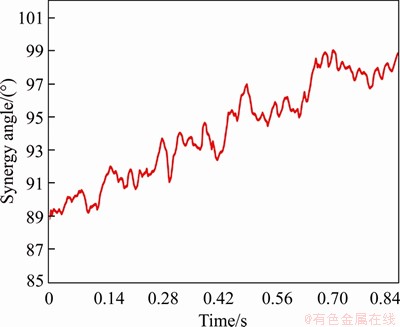
Figure 10 Variation in synergy angle
4.2 Analysis of mass-transfer field synergy
Different flow patterns between the two pipes have different effects on the mass transfer synergy. Velocity vectors and mass-transfer synergy angle distributions between pipes for curtain, droplet columnar and droplet flow patterns are obtained in simulation.
4.2.1 Curtain and droplet columnar flow patterns
Figures 11(a) and (b) show the velocity vector distributions for the curtain flow pattern at 0.5 and 0.7 s, respectively, while Figures 12(a) and (b) show the velocity vector distribution for the droplet columnar flow pattern at 0.5 and 0.8 s, respectively. It is seen that two relatively stable vortexes form on either side of the liquid film in the curtain flow pattern. Vortexes also form on either side of the solution in the droplet columnar flow pattern. With the flow of the solution, the vector distribution changes gradually and vortexes appear continuously. In the absence of air flow, the liquid film is dominated by the continuous action of gravity during the flow process on the pipe wall, and the area of the maximum velocity thus appears in the full-development area. When there is air flow, the velocity is a maximum earlier, possibly in the development zone.
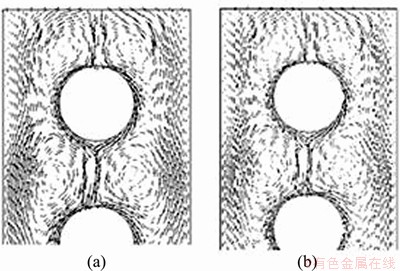
Figure 11 Velocity vectors for curtain flow at 0.5 s (a) and 0.7 s (b)
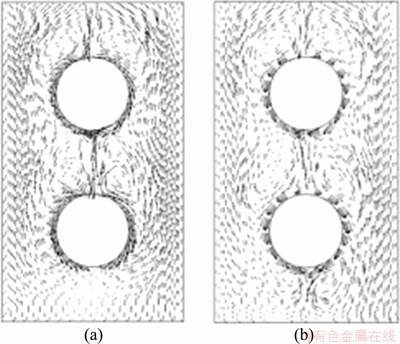
Figure 12 Velocity vectors for droplet columnar flow at 0.5 s (a) and 0.8 s (b)
Figures 13(a) and (b) show the synergy angle distribution for the curtain flow pattern at 0.5 and 0.7 s, respectively, while Figures 14(a) and (b) show the synergy angle distribution for the droplet columnar flow pattern at 0.5 and 0.8 s, respectively. The curtain flow pattern forms a relatively obvious synergy angle distribution zone on the peripheral and inner sides of the liquid membrane. The synergetic angle at the phase interface of the droplet is large, and the distribution of the synergy angle changes with the flow of the solution. Compared with that of the curtain flow pattern, the synergy angle distribution zone of the droplet columnar flow pattern is not particularly obvious. The maximum mass-transfer synergy angles of both the curtain and droplet flow patterns are found in the freefall area and wake area.
4.2.2 Droplet flow pattern
Figures 15(a)–(f) show distributions of the velocity vector field on the wet-air side when the solution between pipes has a droplet flow pattern. Comparing with the previously simulated flow patterns, it is found that the junction between the wet air and dehumidification solution is more likely to generate a vortex, while the velocity vector field of the remainder of the wet air side is more uniform and generates less vortex motion, which indicates that the disturbance on the wet-air side is not large. Starting from 0.25 s, the vortex between the horizontal pipes constantly changes spatial position and size owing to erosion of the dehumidification solution. Compared with the cases of the droplet columnar and curtain flow patterns, in the droplet flow pattern, the vortex generation frequency is higher and there are more vortexes, which enhances the synergy of mass transfer.
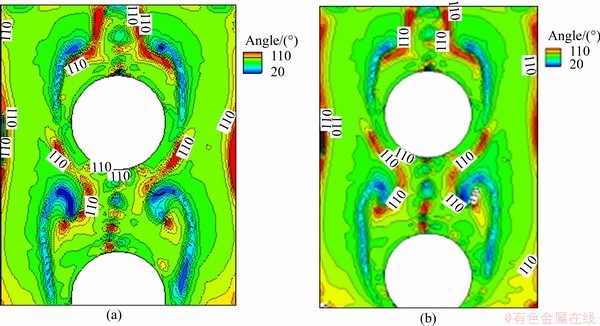
Figure 13 Distribution of synergy angle for curtain flow at 0.5 s (a) and 0.7 s (b)
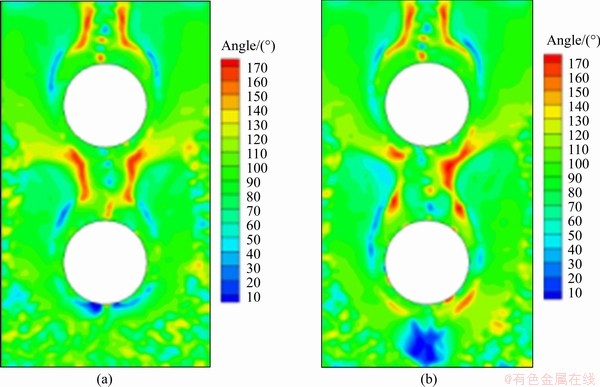
Figure 14 Distribution of synergy angle for droplet columnar flow at 0.5 s (a) and 0.8 s (b)
Figures 16(a) and (b) show the recorded distribution of the mass-transfer synergy angle in one period when the lithium chloride solution has a droplet flow pattern. Comparing with the previously simulated flow patterns, it is found that the synergy angle of the junction between the wet air and dehumidification solution is appreciably different. The maximum synergy angles of mass transfer of about 110° are mostly at the phase interface. For the remainder of the wet air side, the synergy angle is 90° and the synergy is poor. Starting from 0.25 s, the synergy angle of mass transfer constantly changes with the repeated scouring of the desiccation solution. In the simulation, a larger synergy angle (dark red in the figure) and smaller synergy angle (dark blue) are generated, disappear and are regenerated repeatedly. The maximum mass-transfer synergy angles are found in the freefall area, impact area, development area, full-development area and wake area owing to strong disturbance of the droplet flow pattern. In the case of the droplet flow pattern, the continuous disturbance of the droplets on the wet-air side means that the synergy is stronger than that for the droplet columnar and curtain flow patterns.
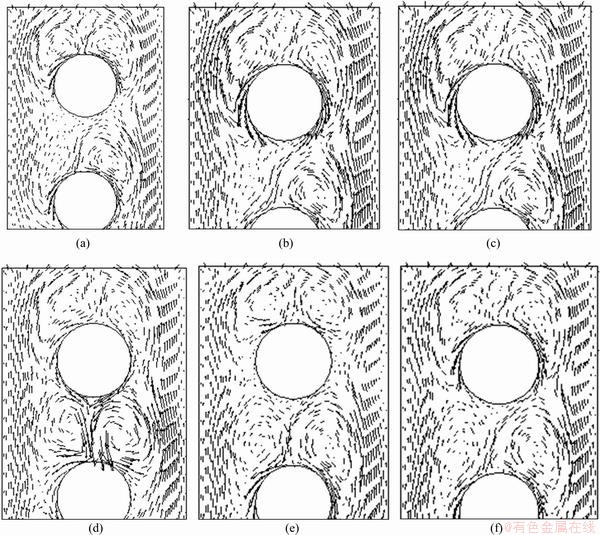
Figure 15 Velocity vectors for droplet flow at (a) 0.25 s, (b) 0.27 s, (c) 0.29 s, (d) 0.31 s, (e) 0.34 s and (f) 0.37 s
4.3 Comparison of mass-transfer synergy angles for different flow patterns
Figure 17 shows the distribution of the mass-transfer synergy angle at 0-0.70 s for curtain, droplet columnar and droplet flow patterns. It is found that within 0-0.24 s, the difference in the synergy angle among the three flow patterns is not large. After 0.24 s, the difference in the synergy angle among the three flow patterns begins to become obvious. The mass transfer synergy angle of the droplet flow pattern changes greatly but finally forms stable oscillation. The amplitudes of the differences in the mass-transfer synergy angle from those of the droplet columnar and curtain flow patterns are consistently small, but slowly rise. Finally, the curtain and droplet columnar flow pattern also form stable oscillation. But the oscillation of droplet flow pattern is larger than that of the curtain and droplet columnar flow pattern. The arithmetic mean synergy angle can be obtained by averaging the synergy angle in the stable oscillation phase. The arithmetic mean synergy angles of droplet, droplet columnar and curtain flow pattern were 98°, 96.5° and 95°, respectively. The cosine value of synergy angle of droplet flow pattern is larger than that of curtain and droplet columnar. According to Eq. (10), the mass transfer synergy of droplet flow pattern is stronger than that of curtain and droplet columnar. On the whole, the mass transfer angle of the droplet flow pattern is higher than the mass transfer angles of the droplet columnar and curtain flow patterns. This is because the disturbance on the wet-air side is much stronger for the droplet flow pattern than for the droplet columnar and curtain flow patterns.Figure 18 presents the power function regression line of the synergy angle, which has the same meaning as Figure 17.
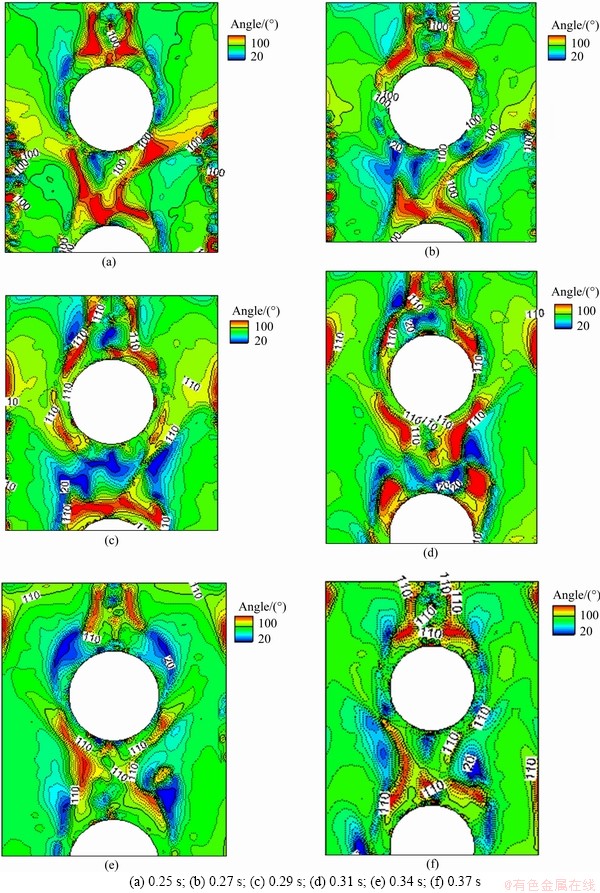
Figure 16 Synergy angle distribution for droplet flow at:
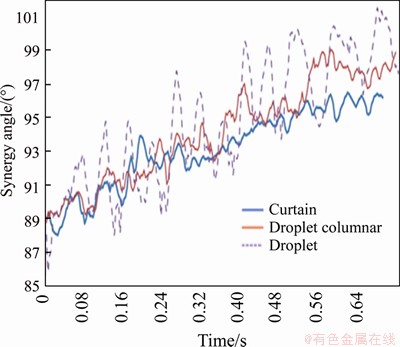
Figure 17 Comparison of synergy angles for different flow patterns
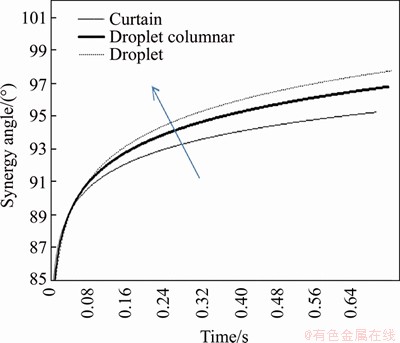
Figure 18 Power-form regression line of synergy angle
4.4 Comparison of heat transfer synergy
The heat transfer synergy angle, composed of temperature vector and velocity vector, can be used to evaluate the synergy of heat transfer. Figure 19 shows that the liquid film on the pipe wall is relatively stable for the curtain flow pattern. Compared with the droplet and droplet columnar flow patterns, the velocity field inside the film fluctuates less and there is no obvious change in the heat transfer synergy angle. The heat transfer synergy angle is higher for droplet and droplet columnar flow patterns than for the stable curtain flow pattern.
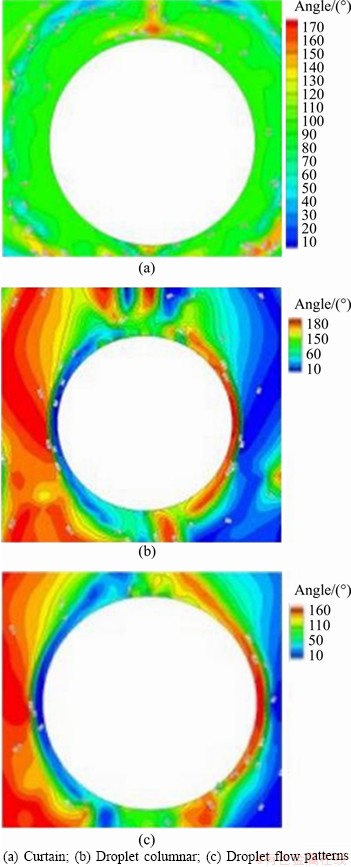
Figure 19 Comparison of heat-transfer synergy angles for:
5 Conclusions
This study simulated the dehumidification process between two horizontal pipes, analyzed the flow pattern between the two pipes and obtained the critical Reynolds numbers of transitions of the flow pattern. The mass transfer synergy angle and heat transfer synergy angle were used to measure the synergy of mass transfer and the synergy of heat transfer respectively, and the distribution characteristics of the wet-air synergy angle were obtained for different flow patterns between pipes. The main results are summarized below:
1) Simulation results showed that there are droplet, droplet columnar and curtain flow patterns between the two horizontal pipes when Re≤45, 45 2) For the intertubular falling-film dehumidification process, the mass-transfer synergy angle increased with time but finally stabilized for all droplet, droplet columnar and curtain flow patterns. 3) When the solution used in intertubular falling-film dehumidification has a droplet flow pattern, owing to rich dynamic behaviors, periodic movement strongly affects the distribution of the synergy angle on the air-side field, so that the synergy angle is larger than that for the curtain flow pattern; that is, the droplet flow pattern can be adjusted to increase the synergy performance. 4) The mass transfer synergy angle of the droplet flow pattern was 98°, higher than 96.5° for the droplet columnar flow pattern and 95° for the curtain flow pattern. With an increase in the solution velocity, the falling film flow tends to have a curtain pattern, and the synergy angle decreases and the synergy worsens. 5) The comparison of the heat transfer synergy of different flow patterns on a pipe wall revealed that fluctuations are greater for droplet and droplet columnar flow patterns than for the stable curtain flow pattern and that the synergy angle of heat transfer is large for the droplet and droplet columnar flow patterns that for the stable curtain flow pattern, such that the synergy of heat transfer for the droplet and droplet columnar flow patterns are better than the synergy for the stable curtain flow pattern. References [1] ZENG Tai-ye, ZHANG Xiao-song, CHEN Yao. Experimental investigation for low-concentration liquid desiccant regeneration with utilization of condensation heat [J]. Journal of Refrigeration, 2018, 39(1): 76-82. (in Chinese) [2] QI Rong-hui, DONG Chuan-shuai, ZHANG Li-zhi. Development of liquid-air mass transfer correlations for liquid desiccant dehumidification considering the liquid/air contact and film instability [J]. International Journal of Heat and Mass Transfer, 2019, 141: 491-502. [3] LIU Xiao-hua, YI Xiao-qin, JIANG Yi. Mass transfer performance comparison of two commonly used liquid desiccants [J]. CIESC Journal, 2009, 60(3): 567-573. (in Chinese) [4] WANG Li, LIAN Zhi-wei, LIU Wei-wei. Analysis of liquid-desiccant dehumidifying system combined with ultrasound atomization technology [J]. Journal of Central South University (Science and Technology), 2011, 42(1): 240-246. (in Chinese) [5] NAIK B K, MUTHUKUMAR P. Experimental investigation and parametric studies on structured packing chamber based liquid desiccant dehumidification and regeneration systems [J]. Building and Environment, 2019, 149: 330-348. [6] OU Xian-hua, CAI Wen-jian, HE Xiong-xiong, ZHAI De-qing. Experimental investigations on heat and mass transfer performances of a liquid desiccant cooling and dehumidification system [J]. Applied Energy, 2018, 220: 164-175. [7] WANG Lei-lei, YOU Shi-jun, WANG Shu-zhong, YANG Xiao-jing. Experimental study on mode transition of falling film flow in horizontal tube bundle [J]. Building Science, 2010, 26(10): 318-323. (in Chinese) [8] YANG Li, WANG Wen, ZHOU Jia-qiang. Numerical simulation of the structural optimization of tube bundles in horizontaltube falling film evaporators [J]. Journal of Shandong Jianzhu University, 2012, 27(2): 193-197. (in Chinese) [9] HOU Hao, BI Qin-cheng, ZHANG Xiao-lan. Numerical research on flow field and temperature field in shell side of horizontal-tube falling-film evaporator [J]. Journal of Central South University (Science and Technology), 2011, 42(12): 3882-3887. (in Chinese) [10] ROGERS J T. Laminar falling film flow and heat transfer characteristics on horizontal pipes [J]. Canadian Journal of Chemical Engineering, 1981, 59: 213-222. [11] CHINNOV E A, KABOV O A. Marangoni effect on wave structure in liquid films [J]. Microgravity Science and Technology, 2007, 19(3, 4): 18-22. [12] DONG Chuan-shuai, LU Lin, WEN Tao. Investigating dehumidification performance of solar-assisted liquid desiccant dehumidifiers considering different surface properties [J]. Energy, 2018, 164: 978-994. [13] JIGE D, MIYATA H, INOUE N. Falling film evaporation of R1234ze(E) and R245fa on a horizontal smooth tube [J]. Experimental Thermal & Fluid Science, 2019, 105: 58-66. [14] ZENG Zhuo-xiong, WANG Zhang-jun, LIU Jian-quan. Numerical analysis of synergy between velocity field and temperature field in finned tubes with different longitudinal vortex generators [J]. Applied Mathematics and Mechanics, 2015, 36(7): 744-755. (in Chinese) [15] WU Shi-yi-hui, LUO Kun, FAN Jian-ren. Flow field synergy analysis and drag reduction design of non-slam check valve [J]. Journal of Zhejiang University (Engineering Science), 2018, 52(1): 29-35. (in Chinese) [16] ZHONG Ying-jie, WANG Xun-ting, HUANG Qi, YANG Zhi-chao, YANG Zang-jinan. A study of heat transfer mechanism in a pulsating flow based on field synergy theory [J]. Journal of Zhejiang University of Technology, 2015, 43(2): 180-184. (in Chinese) [17] LI Fang, ZHU Wen-hui, HE Hu. Numerical optimization on microchannel flow and heat transfer performance based on field synergy principle [J]. International Journal of Heat and Mass Transfer, 2019, 130: 375-385. [18] KILLION J D, GARIMELLA S. Gravity-driven flow of liquid films and droplets in horizontal pipe banks [J]. International Journal of Refrigeration. 2003, 26: 516-526. (Edited by ZHENG Yu-tong) 中文导读 水平管降膜除湿系统中不同流态的场协同性分析 摘要:本文研究了水平管降膜除湿系统中管间液膜的流动方式对传质与传热协同性的影响。利用Fluent软件建立了水平管间除湿溶液的流动模型,研究了管间溶液流型的过渡规律,得到了流型过渡的临界雷诺数,并通过实验验证了模型的正确性。分别以传质协同角和传热协同角作为传质协同性和传热协同性的评价标准,得到了滴状、滴柱状和帘状流态的协同角分布规律。结果表明,液滴、滴柱状和帘状流态的传质协同角随着时间的延长均趋于稳定。液滴流态的平均传质协同角为98°,滴柱状流态的平均传质协同角为96.5°,帘状流态的平均传质协同角为95°。滴状流态的传质协同作用优于滴柱状流态和帘状流态。 关键词:水平管降膜;Fluent软件;液膜流态;协同角;传热传质 Foundation item: Project(2016YFC0700100) supported by the National Key R&D Program of China; Project(JDJQ20160103) supported by the Promotion of the Connotation Development Quota Project of Colleges and Universities-Outstanding Youth of Architectural University, China Received date: 2020-01-09; Accepted date: 2020-04-27 Corresponding author: NIU Run-ping, PhD, Associate Professor; Tel: +86-13911607350; E-mail: niurunping@bucea.edu.cn; ORCID: https://orcid.org/0000-0002-6512-2784

