MIMO-OFDM系统的同步算法
杨春萍,王键,李道本
(北京邮电大学 信息工程学院,北京,100876)
摘 要:针对MIMO-OFDM系统中对同步要求较高的问题,提出一种MIMO-OFDM系统中的时/频同步算法,该算法与其他同步算法的关键区别在于将完备广义互补正交同步码组用作同步序列。对于完备广义互补正交码组,在各分量码不重叠的情况下,具有任何相对相移的任意码以及任意码对的自相关特性和互相关特性都是理想的,这一理想特性使得时/频同步算法简单高效。该同步算法分为4步:(1) 通过信号自相关实现时域上的同步;(2) 通过快速傅里叶变换(FFT)实现频域上同步;(3) 使用相干检测和精确时间同步实现多径分离;(4) 通过相位差分算法实现精确的频偏估计。仿真结果表明:即使在低信噪比如0 dB的多径快衰落信道中,MIMO-OFDM系统也可以在时域和频域上实现精确同步,同时具有高度稳定性和可靠性。
关键词:MIMO;OFDM;同步;互补正交码码;LS码
中图分类号:TN911.23 文献标志码:A 文章编号:1672-7207(2010)02-0578-07
Synchronization algorithm for MIMO-OFDM system
YANG Chun-ping, WANG Jian, LI Dao-ben
(School of Information Engineering, Beijing University of Posts and Telecommunications, Beijing 100876, China)
Abstract: Aiming at the problem of higher requirement for synchronization in MIMO-OFDM (Multiple input multiple output-orthogonal frequency devision multiplexing) system, a time/frequency synchronization algorithm in MIMO system was proposed, in which the key difference with other synchronization algorithms was to use the perfect complete generalized complementary orthogonal loosely synchronous code groups as the synchronization sequence. As regard to perfect complete generalized complementary orthogonal code groups, the cross-correlation and auto-correlation for any relative shifts between any two codes or between any code pairs were all 0 in the case of each component code that was not overlapped. This ideal property makes the time/frequency synchronization algorithm simple and efficient. The synchronization algorithm was divided into four stages: (1) synchronization in time domain by signal autocorrelation; (2) synchronization in frequency domain by Fast Fourier Transform (FFT); (3) multi-path dissociation using coherent detection and fine time synchronization; (4) fine frequency offset estimation by phase rotation. The simulation results show that even in the low signal noise ratio such as 0 dB multi-path fast fading channel, the MIMO system can get synchronized both in time domain and frequency domain with high stability and reliability.
Key words: MIMO; OFDM; synchronization; complementary orthogonal code; LS code
多输入多输出(Multiple input multiple output, MIMO)技术已经作为用于提供3G/B3G/4G无线系统[1]中所要求的频谱效率的关键方法之一,正交频分复用(Orthogonal frequency devision multiplexing, OFDM)是作为频率选择性衰落信道上进行高速数据传输的有效多载波调制方案[2],将OFDM与MIMO 技术相结合将成为高频谱效率无线传输的最佳方案[3]。类似于SISO-OFDM系统,MIMO-OFDM系统对同步误差非常敏感[4-5]。OFDM中的频偏估计很关键,因为任何频偏会引起子信道正交性丧失,这导致载波间干扰 (ICI)以及性能下降。通常,使用从所有发射天线同时发射的训练符号以达到同步[6-8],本文作者所提出的同步算法与其他算法的关键区别在于使用正交完备互补(OCC) LS码(Link space code)作为同步序列。正交完备互补码源自Golay码[9]、Turyn码[10]和Suehiro码[11]。Chen等[12]研究了OCC码在CDMA系统中的应用;Li等[13-14]提出一种OCC码,其自相关函数对于除了零相移之外的所有相移都为0,互相关函数对于所有可能的相移都为0。正交完备互补LS 码组的这一理想特性使得所提出的时频同步算法简单且有效;Wang等[15]提出了仅使用一对LS码作为同步序列的同步算法,由于每一个发射天线都需要占用1个LS码字,因此,这个方案最多仅可以支持2个发射天线。这里,本文作者首先提出使用正交完备互补LS码组作为同步序列,提出新结构的同步信道,并且提出新的时/频同步方案。
1 完备广义互补正交码组
通常,OCC码的正交性是联合地基于一组基本码,而不是像传统的扩频码中基于单码。并且对于完备广义互补正交码组,任何码对之间的相对相移必须保证零互相关和异步自相关。在本文中,完备广义互补正交码组表示为: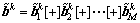 ,k=1, 2,…, K。其中:
,k=1, 2,…, K。其中: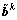 具有基本码
具有基本码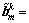
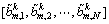 ,长度为N。这个完备广义互补正交码组的自/互相关特性可以表述如下:
,长度为N。这个完备广义互补正交码组的自/互相关特性可以表述如下:
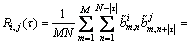
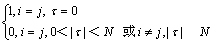
OCC码的处理增益(PG)等于所有基本码的总长,即 PG=M×N。Han等[11]证明了该码组数等于基本码数,即K=M=PG/N,并且在M和N之间没有任何约束。
下面举1个基本码长L=2的完备广义互补正交码组的例子。假定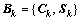 (k=1, 2)是1个LS码,也是1个完备广义互补正交码组
(k=1, 2)是1个LS码,也是1个完备广义互补正交码组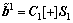 ;
;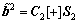 。其中:
。其中: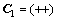 ,
,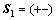 ;
; ,
,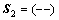 [13]。则这个OCC码组矩阵为:
[13]。则这个OCC码组矩阵为:
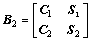 (2)
(2)
设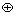 表示移位相加运算,则
表示移位相加运算,则
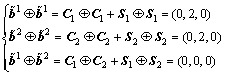 (3)
(3)
它显示了OCC码的理想自相关和互相关特性。
高维的完备广义互补正交码组可以通过Hadamard矩阵Kronecker乘积(直积)从低维的完备广义互补正交码组产生[16]。
假定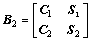 是1个完备广义互补正交码组矩阵,K=2,那么,
是1个完备广义互补正交码组矩阵,K=2,那么,
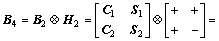
 (4)
(4)
这是一个K=4的完备广义互补正交码组矩阵。通常,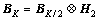 。
。
在该系统中,发射天线的同步序列是完备广义互补正交码组矩阵的1行,保护零插在基本码之间。保护零是用来避免码组的基本码的重叠,因此,保护零的时间长度应当大于信道的最大时延扩展。由于时频同步算法的需要,同步序列在OFDM帧之前被发送2次。称2次发送的同步序列为OFDM帧的同步信道。图1所示为分配给发射天线的同步信道的结构,可见:在每组同步序列中,前半部分的内容与后半部分的内容相同,即对应完备广义互补正交码组矩阵的1行的内容共176个码片被发送2次。
2 信号模型
1个Q×L空时系统在发射机上具有Q条天线,在接收机上具有L条天线。进行如下假定:Sq, n为来自第q条发射天线第n个发射的OFDM符号的频域信号;sq, n为来自第q条发射天线第n条发射的OFDM符号的时域信号;ηql, k, n是在第q条发射天线和第l条接收天线之间在第n条所发射的OFDM符号时刻上的第k个子载波信道冲激响应;hql, m, n是在第q个发射天线和第l条接收天线之间在第n条所发射的OFDM符号时刻上的第m条路径的信道冲激响应;Rl, n是来自第l条接收天线的第n条接收的OFDM符号的频域信号;rl, n是来自第l条接收天线的第n个接收的OFDM符号的时域信号;pq是第q条发射天线的同步序列,pq, n是这个序列的第n条码片。假定Lcp是同步序列的码片长度,则同步信道的码片长度是2Lcp。假定tcp是同步序列的1个码片的信号时间,则码片速率为Fcp=1/tcp。
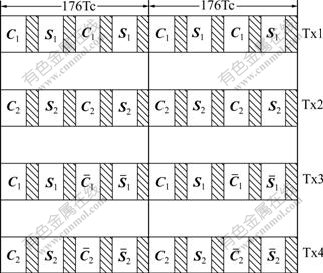
图1 发射天线的同步信道结构
Fig.1 Structure of synchronization channels of transmit antennas
来自第q条发射天线第n个OFDM符号的N点反数字傅里叶变换(IDFT)输出序列给定为
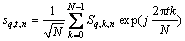 , 0≤t≤N-1
, 0≤t≤N-1
在去除保护间隔后所接收的样值序列为
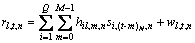
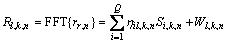
其中:wl, t, n是方差为N0的复加性高斯白噪声样值;wl, k, n是wl, t, n的N点傅里叶变换。对于同步信道中的同步序列信号,由第l条接收天线接收的第n个码 片为:
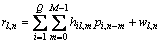
3 同步算法
3.1 时域上的基于自相关同步
符号定时恢复依赖于搜索训练序列。训练序列在时域上分成内容相同的前、后2部分,即序列的第1半与第2半,它们的内容相同。在经过信道传送之后第1半和第2半的内容将仍然相同,只是它们之间由载波频偏引起的相位差不同。
假定接收机处的频偏为?f,由第l个接收天线接收的第n个码片为:
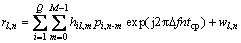 (5)
(5)
考虑其中第1半与第2半(在时间顺序上)相同的同步信道,只是由载波频偏引起的相移不同。如果第1半的样值共轭乘以第2半的对应样值(Lcptcp),则信道的影响应当被抵消,结果是有约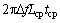 的相位旋转。在帧头上,这些对样值的每一对乘积具有近似的相位。各对乘积之和为:
的相位旋转。在帧头上,这些对样值的每一对乘积具有近似的相位。各对乘积之和为:
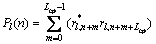 (6)
(6)
并且在该搜索窗口中的信号能量为:
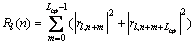 (7)
(7)
根据完备广义互补正交码组的特性,若信道的最大时延扩展小于同步序列基本码之间的保护零的时间长度,则非周期自相关旁瓣和分配给发射天线的所有同步序列之间的互相关都为0。因此,若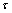 为同步信道序列到达接收天线的正确时刻,则此时各对乘积之和为:
为同步信道序列到达接收天线的正确时刻,则此时各对乘积之和为:
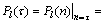
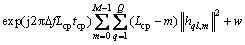 (8)
(8)
其中:m为发射-接收天线对之间的多径条数;q为发射天线条数;w为时刻τ上的噪声,具有时延的LS
码之间的码间干扰。 可见:对于第l条接收天线,式(8)中的第1部分是发射-接收天线对(总共Q对)之间的所有多径(每个发射-接收天线对有M条路径)的功率加权和,并且第2部分w是时刻τ上的噪声。此外,在这个等式中,频偏的影响仅仅是多路径功率之和在度量上的相移。假定:
 (9)
(9)
其中:l是接收天线条数。这个等式右边的第1部分是发射-接收天线对(共M×Q×L条路径)之间所有多径的功率加权和;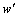 是噪声和时延的LS码的ICI噪声功率,并且频偏对这个算法的结果没有任何影响。假定:
是噪声和时延的LS码的ICI噪声功率,并且频偏对这个算法的结果没有任何影响。假定:
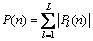
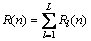 (10)
(10)
定时度量为
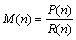 (11)
(11)
频偏对该定时度量没有影响。因此,该算法甚至在接收机具有大频偏的情况下也可以显示良好的性能。在无线多径衰落环境中,这个定时度量的最大值反映到达接收机天线最大功率的路径的正确时刻。
3.2 频域上基于FFT的同步
假定在接收机上有?f的频偏,对于由第l个接收天线接收的同步信道信号,同步序列前、后部分的主
要区别在于相移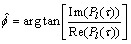 ,其中:
,其中: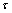 是步骤1算法的输出,为同步信道序列到达接收机天线的时刻;
是步骤1算法的输出,为同步信道序列到达接收机天线的时刻;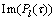 和
和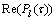 分别为
分别为 的虚部和实部。若
的虚部和实部。若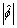 可以保证小于
可以保证小于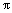 ,则频偏估计为
,则频偏估计为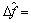
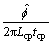 ,否则,实际频偏将为
,否则,实际频偏将为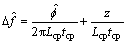 ,其中,z为整数。任何具有整数部分的频偏不能通过这个基于相移的频偏估计器来纠正。通过部分地纠正这个小数频偏,可以避免相邻载波干扰,并且其余的整数部分频偏可以由基于FFT粗略频偏估计器来 找到。
,其中,z为整数。任何具有整数部分的频偏不能通过这个基于相移的频偏估计器来纠正。通过部分地纠正这个小数频偏,可以避免相邻载波干扰,并且其余的整数部分频偏可以由基于FFT粗略频偏估计器来 找到。
步骤1:小数频偏估计为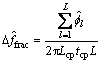 。经过同步信道序列时间间隔
。经过同步信道序列时间间隔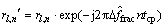 ,将它乘以
,将它乘以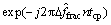 ,这个小数频偏可以从所接收的信号序列中去掉。
,这个小数频偏可以从所接收的信号序列中去掉。
步骤2:基于FFT粗略频偏估计器将给出这个频偏的整数部分。
(1) 对于所有接收天线,信号在小数频偏移除之后分别乘以逐码片分配给发射天线的每个同步信道 序列。
(2) 将这些时域序列(对于所有发射-接收天线对来说为Q×L 序列)通过FFT算法转换成频域序列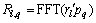 ,1≤l≤L, 1≤q≤Q。
,1≤l≤L, 1≤q≤Q。
(3) 将所有频域序列的幅值相加得到频域检测统
计序列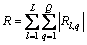 。
。
(4) 具有最大幅值的频点将给出整数频偏。
假定这个点为n,则整数频偏为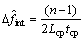 。这个基于FFT整数频偏估计的频率精度为
。这个基于FFT整数频偏估计的频率精度为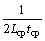 。
。
步骤3:将小数频偏估计和整数频偏估计相加得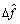 :
:
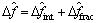 (12)
(12)
3.3 基于相干检测的多径分离和精确时间同步
经过步骤1之后,系统得到粗略的时间获取,得到具有最大功率的路径到达接收机天线的正确时刻,包括整数和小数频偏的多数频偏通过步骤2被检测并且去除。假定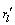 是由第l个接收天线接收的去除粗略频偏的信号,并且
是由第l个接收天线接收的去除粗略频偏的信号,并且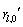 是在粗略时间同步算法给出的时刻上由第l个接收天线接收的信号,并假定:
是在粗略时间同步算法给出的时刻上由第l个接收天线接收的信号,并假定:
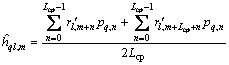 ,
,
mmin<m<mmax, mmin<0, mmax>0 (13)
其中:mmin<m<mmax,是找到精确时间同步的时间范围。由于同步序列的理想自相关函数和互相关函数在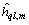 之间没有码间干扰,若在时间m上出现1条路径,则
之间没有码间干扰,若在时间m上出现1条路径,则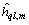 就是这个无线路径的信道响应;若在时间m上没有路径,则由于同步序列的扩展运算
就是这个无线路径的信道响应;若在时间m上没有路径,则由于同步序列的扩展运算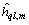 就是具有极小方差的零均值高斯噪声,对于所有接收天 线,使用同一算法,得
就是具有极小方差的零均值高斯噪声,对于所有接收天 线,使用同一算法,得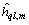 。其中:q∈{1, 2, …, Q};l∈{1, 2, …, L};m∈{mmin, …, mmax};q为发射天线条数;l为接收天线条数;m为时间。基于
。其中:q∈{1, 2, …, Q};l∈{1, 2, …, L};m∈{mmin, …, mmax};q为发射天线条数;l为接收天线条数;m为时间。基于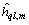 ,得
,得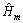 。其
。其
中:m={mmin, …, mmax};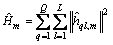 ,m∈{mmin, …, mmax}。
,m∈{mmin, …, mmax}。
在时间m上,若有路径到达接收天线,则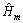 是所有路径的功率之和;若没有路径到达接收天线,则
是所有路径的功率之和;若没有路径到达接收天线,则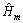 就是噪声功率之和。最后,通过滑动求和窗口,从所有的
就是噪声功率之和。最后,通过滑动求和窗口,从所有的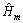 得到精确时间获取。
得到精确时间获取。
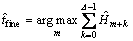 (14)
(14)
其中: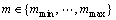 ;
;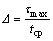 ;
;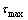 为信道的最大时延扩展。在这个步骤中,精确时间同步算法给出第1路径而不是具有最大功率的路径到达接收天线的准确时刻,显然这增强了无线多径快衰落信道环境下时间同步算法的稳定性。
为信道的最大时延扩展。在这个步骤中,精确时间同步算法给出第1路径而不是具有最大功率的路径到达接收天线的准确时刻,显然这增强了无线多径快衰落信道环境下时间同步算法的稳定性。
3.4 基于相位旋转的精确频偏估计
经过步骤3后,系统已经得到第1路径到达接收机天线的时间。假定该时间为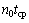 ,则
,则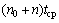 为第n条路径到达接收机天线的时间。根据完备广义互补正交码组的特性,对于第l个发射天线和第q个接收天线简单的第m条路径,可以在同步信道序列第1半和第2半的时间上分别得到2个信道冲激响应:
为第n条路径到达接收机天线的时间。根据完备广义互补正交码组的特性,对于第l个发射天线和第q个接收天线简单的第m条路径,可以在同步信道序列第1半和第2半的时间上分别得到2个信道冲激响应:
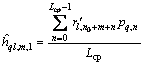 ,
,
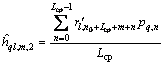 (15)
(15)
若接收机具有?f频偏,则频率估计为
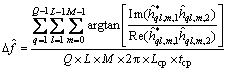 (16)
(16)
这里需注意的是:
(1) 整数频偏估计在步骤2的算法期间已经完成,因此,由这个算法估计的频偏仅是小数频偏。
(2) 步骤4的关键在于所估计的精确频偏是在发射-接收天线对之间所有路径的频偏平均值。因此,在无线多径衰落信道环境下,这个算法具有极大的稳定性和可靠性。
4 仿真结果
对所提出的算法在Linux OS环境下使用MATLAB 对4Tx-2Rx MIMO-OFDM系统进行测试。该MIMO-OFDM系统的载波频率为2.0 GHz,带宽为 5 MHz。在发射机和接收机之间的无线信道模型采用ITU-VA信道。接收机的接收速率为250 km/h,因此,多普勒扩展频率为460 Hz。帧间隔为10 ms,帧结构包含2部分:第1部分是同步信道,第2部分是数据信道。完备广义互补正交码组从LS码组[13]通过Hadamard矩阵Kronecker乘积得到,基本码长为32 bit。同步信道的码片速率为3.84 Mchip/s,最大时延扩展为11个码片时间长,因此,基本分量码之间的保护零为12。同步序列有(32+12)×4=176个码片,同步信道有176×2=352个码片。
时间同步算法在不同频偏条件下的性能如图2所示。在时间同步算法中,对于所接收信号的每一帧,首先进行粗时间同步,然后,进行粗频率同步和频率补偿,最后,进行精时间同步和精频率同步。在MIMO-OFDM系统中,认为只有当获得第一路径的到达时间时,同步过程才算成功。因为在最初的同步阶段,系统有可能存在较大的频率偏差,因此,需要时间同步算法拥有抵制频偏的能力。仿真结果表明:在各种频偏条件下,本文所提出的时间同步算法甚至在大频偏时也表现优越;当频偏为60 kHz时,算法的成功率与零频偏时没有差别;当信噪比为0 dB时,系统即可以达到精确的时间同步。此外,对于4Tx-2Rx MIMO-OFDM系统,由联合算法所得信噪比与由Wang等[15]提出的算法及经典的同步算法[17-18]所得信噪比相比,分别提高近3 dB和5 dB。
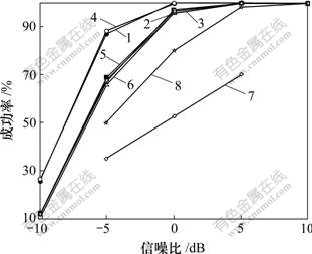
1—天线1和天线2联合,频率为60 Hz;2—天线1,频率为60 Hz;3—天线2,频率为60 Hz;4—天线1和天线2联合,频率为0 Hz;5—天线1,0 Hz;6—天线2,频率为0 Hz;7—经典算法,频率为0 Hz;8—LS同步算法,频率为0 Hz
图2 时间同步算法的成功率
Fig.2 Success rates of time synchronization algorithm
图3所示为整数频偏估计算法的成功率。512点FFT转换用于粗同步估计算法中,可获得的精度可达7.5 kHz,并且估计范围为-1.9~1.9 MHz。对于估计范围内的每个频点,执行1 000次仿真并且总仿真次数为512 000。对于每次仿真,若算法获得正确的频点,则频率估计成功,否则失败。从图3可以看到:在4Tx-2Rx MIMO-OFDM系统中,频率估计算法效果较好;当信噪比为0 dB时,整数频偏估计在仿真中没有误差。
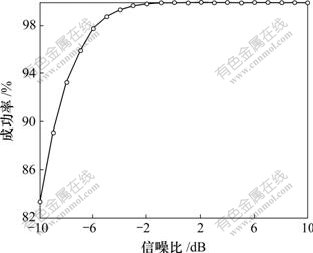
图3 整数频偏估计算法的成功率
Fig.3 Success rate of integral frequency offset estimation algorithm
分数频偏估计算法的均方误差如图4所示。根据系统参数,分数估计算法的估计范围为-10.9~10.9 kHz。因为在信道冲激相位旋转上的精确频率估计算法需要第一路径的到达时间,该算法应当在系统获得精确时间同步之后执行。由图4可见:对于4Tx-2Rx MIMO-OFDM系统,2个接收机天线的联合频率估计显示比在单个天线上的频率估计具有更好的性能,其信噪比高于文献[15]中方案的信噪比4~5 dB。这是合理的,因为更多的天线导致子路径更独立,更多的估计值导致结果更精确。而且在2个接收机天线上使用联合估计算法时,5 kHz频偏和0 Hz频偏时的均方误差几乎是相同的。该结果还表明:在估计范围内,通过采用信道冲激相位旋转的精确频率估计算法可以满足系统要求。

1—0 Hz频偏,2个接收机联合;2—5 kHz频偏,2个接收机联合;3—0 Hz频偏,1个接收机频率估计器;4—5 kHz频偏,1个接收机频率估计器
图 4 精确频偏估计算法的均方误差
Fig.4 Error variances of fine frequency offset estimation algorithms
5 结论
(1) 使用完备广义互补正交LS码组实现MIMO- OFDM系统同步,设计了一种新结构的同步信道,提出了一种新颖的精确时间获取和精确频偏获取方案。完备广义互补正交LS码组与发射天线相关联并且作为OFDM帧的同步序列发送。完备广义互补正交LS码组使得所提出的MIMO-OFDM系统同步更容易、更准确。
(2) 该同步算法甚至在低信噪比的移动多径快衰落信道环境下也表现出理想的性能。在各种频偏条件下,本文所提出的时间同步算法性能优越:当频偏为60 kHz时,算法的成功率与零频偏时的成功率没有差别;当信噪比为0 dB时,系统即可以达到时间同步。此外,对于4Tx-2Rx MIMO-OFDM系统,联合算法与经典的同步算法等相比,信噪比较高。
参考文献:
[1] Foschini G, Gans M. On limits of wireless communications in a fading environment when using multiple antennas[J]. Wireless Personal Commun, 1998, 6(3): 311-335.
[2] Bingham J A C. Multicarrier modulation for data transmission: an idea whose time has come[J]. IEEE Commun Mag 1990, 28(5): 5-14.
[3] ZHANG Wei, XIA Xiang-gen, Ben L K. Space-time/frequency coding for MIMO-OFDM in next generation broadband wireless systems[J]. Wireless Communications IEEE, 2007, 14(3): 32-43.
[4] van de Beek J J, Sandell M, Borjesson P Q. ML estimation of time and frequency offset in OFDM systems[J]. IEEE Trans Signal Processing, 1997, 45(7): 1800-1805.
[5] Pollet T, Bladel M V, Moeneclaey M. BER sensitivity of OFDM systems to carrier frequency offset and Wiener phase noise[J]. IEEE Trans on Communications, 1995, 43(2-4pt 1): 191-193.
[6] Mody A N, Stuber G L. Synchronization for MIMO-OFDM Systems[C]//IEEE Global Communications Conference, San Antonio, USA, 2001: 509-513.
[7] Schenk T C W, van Zelst A. Frequency synchronization for MIMO-OFDM wireless LAN systems[C]//Vehicular Technology Conference. Orlando, 2003: 781-785.
[8] Jiang F, Song M, Song J. OFDM frame synchronization based on energy difference of the received preamble[J]. Journal of China University of Posts and Telecommunications, 2007, 14(1): 96-99.
[9] Groenewald J M, Maharaj B T. MIMO channel synchronization using Golay Complementary Pairs[C]//AFRICON2007. 2007: 1-5.
[10] Turyn R. Ambiguity function of complementary sequences[J]. IEEE Trans on Information Theory, 1963(1): 46-47.
[11] HAN Cheng-gao, Hashimoto T, Suehiro N. A novel construction method of zero-correlation zone sequences based on complete complementary codes[C]//IEEE International Symposium on Information Theory. Toronto, Canada, 2008: 1931-1934.
[12] Chen H H, Chiu H W. Generation of perfect orthogonal complementary codes for their applications in interference-free CDMA systems[J]. Proceeding of Personal, Indoor and Mobile Radio Communications, 2004(1): 734-738.
[13] Li D. The perspectives of large area synchronous CDMA technology for the fourth-generation mobile radio[J]. IEEE Commun Mag, 2003, 41(3): 114-118.
[14] Li D. A high spectral efficient multiple access code[J]. Chinese Journal of Electronics, 1999, 8(7): 11-13.
[15] Wang J, Lin J, Li D. Synchronization for MIMO-OFDM systems with loosely synchronous (LS) codes[C]//WiCom. Shanghai, 2007: 254-258.
[16] Lindsey W C, Simon M K. Telecommunication systems engineering[M]. New Jersey: Prentice Hall, 1973.
[17] Yun H K, Song I, Yoon S, et al. An efficient frequency offset estimator for OFDM systems and its performance characteristics[J]. IEEE Transactions on Vehicular Technology, 2001, 50(5): 1307-1312.
[18] Landstrom D, Wilsom S K, van de Beek J J, et al. Symbol time offset estimation in coherent OFDM systems[J]. IEEE Transactions on Communication, 2002, 50(4): 545-549.
收稿日期:2008-11-29;修回日期:2009-02-07
基金项目:国家自然科学基金资助项目(90604035)
通信作者:杨春萍(1973-),女,辽宁丹东人,博士研究生,从事信道编译码研究;电话:13522701818;E-mail: waitroad@sohu.com
(编辑 陈灿华)