DOI: 10.11817/j.issn.1672-7207.2015.08.048

考虑偶然偏心的消能减震优化设计

陈敏¹，陈伯望¹，贺国京¹，刘畅²

(1. 中南林业科技大学 土木工程与力学学院，湖南 长沙，410004；

2. 悉地国际设计顾问(深圳)有限公司，广东 深圳，518048)

摘要：基于偶然偏心增大结构的地震反应而影响减震结构消能部件的耗能效果，提出一种黏性液体阻尼器与防屈曲支撑混合减震策略：将阻尼器安装在底部隔震层消耗地震能量，防屈曲支撑安装在隔震层以上房屋四角，以便小震时提高结构抗扭刚度，减小偶然偏心的影响，大震时消耗地震能量。选择2栋长宽比分别为1.00和2.33的10层框架结构，采用ETABS与PERFORM-3D分别进行弹性与弹塑性时程分析。研究结果表明：偶然偏心对减震结构消能能力的影响不容忽视；当隔震层阻尼器适量时，增大防屈曲支撑抗侧刚度，消能减震效果显著改善；该减震策略所需消能部件较少，可确保建筑空间的利用效率，是一种具有实用价值的消能减震优化设计方法。

关键词：偶然偏心; 消能减震; 时程分析; 优化

中图分类号：TU352.1; TU375.4             文献标志码：A         文章编号：1672-7207(2015)08-3124-07

Energy dissipation optimal design considering accidental eccentricity of structures

CHEN Min¹, CHEN Bowang¹, HE Guojing¹, LIU Chang²

(1. College of Civil Engineering and Mechanics,

Central South University of Forestry and Technology, Changsha 410004, China;

2. CCDI Group, Shenzhen 518048, China)

Abstract: Considering that accidental eccentricity magnifies the seismic response of certain structure and has impact on the energy dissipation components in structures, a combined energy dissipation strategy blending viscous-fluid damper with buckling-restrained brace was put forward. Dampers were installed on the isolation layer at the bottom to dissipate seismic energy, and buckling-restrained brace was installed at the four corners of the building above the isolation layer,which enhances torsional rigidity of the structure and relieves the impact of accidental eccentricity and facilitates dissipating seismic energy in earthquake. Besides, two 10-storey-framework buildings with length-width ratios of 1.00 and 2.33 were selected and elastic analysis and elastic-plastic time-history analysis were made by adopting ETABS and PERFORM-3D. The results show that the impact of accidental eccentricity on the dissipation capacity of damping structure can not be ignored. With a proper number of dampers at the isolation layer, the seismic response control effect is greatly improved when lateral rigidity of buckling-restrained brace is increased. This energy dissipation strategy requires fewer dissipation components and meanwhile can ensure the utilization ratio of architectural space. Therefore, it is an optimized design for energy dissipation structures and has practical value.

Key words: accidental eccentricity; energy dissipation; time-history analysis; optimization

近几十年来，高烈度区采用消能减震方式对建筑结构进行保护受到结构设计师青睐^[1-2]。人们还对消能减震结构的优化设计展开研究，以便减少所需消能部件的数量以及对建筑空间的不利影响^[3-7]。但在工程实际中，这些成果难以推广：要么需要结构工程师具有较深的专业基础，要么因为实际工程结构复杂，需要考虑偏心、偶然偏心等因素的影响，而相关研究常常基于一些假定，将复杂问题简单化。为此，陈敏等^[8-9]基于基础隔震理论提出了消能减震结构的优化设计方法。这种方法通过调整结构底部第2~3层的层高，使底部第2层或第3层的固有频率ω_n 与场地特征频率ω相等或接近，只需在底部第2~3层安装少量的黏性液体阻尼器便可取得很好的减震效果。但该方法主要针对规则结构，并忽略了偶然偏心的影响。而实际工程即使规则对称，偶然偏心总是存在，因此，该优化方法必须加以完善。为此，本文作者通过算例针对消能减震结构中偶然偏心的影响进行分析，并提出黏性液体阻尼器与防屈曲支撑(buckling-restrained brace,BRB)混合减震策略，通过弹性与弹塑性时程分析其减震效果。

1  理论背景

1.1  偶然偏心的成因

我国“建筑抗震设计规范”^[10]强调建筑设计宜择优选用规则的形体。然而，即使平面布置规则对称，计算地震作用时也应考虑偶然偏心的影响。偶然偏心的产生有2方面的原因^[11-12]：一是质量分布的随机性造成楼层质量中心偏移以及刚度不确定性造成刚度中心偏移，这归类为结构本身的原因；二是地震波传递不仅产生平动分量，而且会产生转动分量。偶然偏心导致偶然扭转，而扭转与平动的耦联将使结构出现更大的地震响应。

1.2  平扭耦联运动方程

多层结构的立体质点系在地震动作用下的运动微分方程如下：

          (1)

式中：M为质量矩阵；K为刚度矩阵；m_x，m_y和m_φ分别为X方向、Y方向质量对角阵和楼板相对于质心转动惯量对角阵；，为m_x与结构楼层质心Y坐标矩阵的乘积；，为m_y与结构楼层质心X坐标矩阵的乘积；K_xx为体系X向总抗侧刚度矩阵；K_yy为体系Y向总抗侧刚度矩阵；K_φφ为体系总抗扭刚度矩阵；，为体系X向抗侧刚度矩阵与其中抗侧力构件至所在楼盖质心垂直距离y_i的乘积；，为体系Y向抗侧刚度矩阵与其中抗侧力构件至所在楼盖质心垂直距离x_i的乘积；C为阻尼矩阵；U为体系位移向量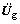；为地震动加速度向量。从质量矩阵M和刚度矩阵K的表达式看出，扭转振动的出现将导致与平动的耦联反应，使结构的地震响应加剧。事实上，由偶然偏心导致的扭转振动不十分剧烈，但也不容忽视。

2  混合减震策略

提高结构的抗扭刚度是减小因偶然偏心产生扭转振动的有效途径。文献[8]基于隔震理论提出的减震结构优化设计方法，关键要求底部隔震层固有频率与场地特征频率接近；隔震层较柔有利于安装于此的黏性液体阻尼器消耗更多的地震能量，因此，提高结构的抗扭刚度从隔震层以上楼层着手会比较有利。可以考虑在隔震层以上的结构四周布置防屈曲支撑，在多遇地震下提高抗扭刚度，在罕遇地震下通过拉压变形消耗地震能量以更好地保护主体结构。图1所示为混合减震示意图。假设底部2层为隔震层，安装黏性液体阻尼器；在第3层以上的四角安装防屈曲支撑，以提高结构抗扭刚度。

2.1  消能装置力学模型

2.1.1  黏性液体阻尼器

经典的泰勒液体阻尼器采用Maxwell模型，可简化为^[13]

            (2)

其中：C₀为零频率阻尼系数；x为相对位移；α为阻尼器两端相对速度的幂，在0.5~2.0之间取值；sgn为正负号函数。式(2)考虑了阻尼器的非线性特征。图2所示为泰勒液体阻尼器力p与位移x关系曲线，表明只要出现相对位移，阻尼器即开始耗能工作，椭圆面积为1个工作周期消耗的能量。

2.1.2  防屈曲支撑

防屈曲支撑力学模型常采用Bouc-Wen模型^[14]，表示为

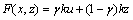             (3)

图1  混合减震结构示意图

Fig. 1  Diagrams of hybrid control structure

图2  黏性液体阻尼器力-位移曲线

Fig. 2  Force-displacement loop of fluid dampers

其中：；，和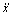分别为系统的位移、速度和加速度；u为外部激励；z为Bouc-Wen滞回非线性恢复力；A，n，α和β为滞回常数。

李国强等^[15]提出了适合防屈曲支撑的非线性滞回模型，并建立了刚度方程。图3所示为BRB支撑常见的滞回关系曲线。

2.2  隔震层设计

黏性液体阻尼器被认为是一种只提供阻尼不提供刚度的消能部件，因此，隔震层设计主要通过调整隔震层抗侧刚度实现^[9]。对于新建的消能减震结构可以初选底部2层为隔震层，当抗侧力构件材料强度、截面尺寸确定后，可通过振型分析计算出隔震层层高。振型分析计算式如下：

             (4)

式中：k_b和m_b分别为隔震层刚度矩阵与质量矩阵；ω_n为隔震层固有频率或基本频率，赋值ω_n为场地特征频率ω。假定隔震层层高相等，则式(4)不难求解。若隔震层层高不合理或不满足建筑设计要求，则可调整隔震层楼层数量以及抗侧力构件相关参数。

图3  防屈曲支撑滞回模型

Fig. 3  Hysteresis curve of buckling-restrained brace

2.3  防屈曲支撑布置策略

防屈曲支撑在此用来提高减震结构的抗扭刚度，宜优先布置在隔震层以上楼层的四角，如图1所示。防屈曲支撑滞回耗能性能由内核芯材决定，其初始抗侧刚度计算式为^[16]

    (5)

式中：E为芯材弹性模量；A为芯材截面积；θ为防屈曲支撑与框架梁的夹角；h为层高。赵瑛等^[16]认为防屈曲支撑的屈服位移仅由内核单元材料强度f_y、层高h、支撑与框架梁之间的夹角θ决定。若芯材选用Q235钢，则30°≤θ≤60°，防屈曲支撑的屈服位移角在区间[1/438, 1/380]内。对于混凝土框架结构，多遇地震下防屈曲支撑将不会屈服。

所需防屈曲支撑数量可通过平扭周期比、弹性和弹塑性时程分析最终确定^[17]。建议防屈曲支撑优先布置在结构四周是考虑到布置在四周可提供较大的抗扭刚度，并减小对建筑空间的影响。

3  算例分析

选择2栋10层、长宽比不同的框架结构作为算例，分析偶然偏心在消能减震设计中的不利影响，提出对策。图4所示为2栋框架结构的平面示意图，长宽比分别为1.00和2.33。

3.1  工程概况

工程所在地区设防烈度8度，设计基本地震加速度为0.30g(1g=9.8 m/s²)，Ⅱ类场地，设计地震分组为第1组。第1~5层框架柱截面长×宽为650 mm×650 mm，混凝土强度等级为C40；第6~10层框架柱截面长×宽为600 mm×600 mm，混凝土强度等级为C35；框架梁截面长×宽为300 mm×750 mm，次梁截面长×宽为300 mm×650 mm。楼板厚度均为100 mm，梁板混凝土强度等级为C30。结构标准层层高为4 000 mm，隔震层层高由计算确定。表1所示为框架柱配筋。

3.2  消能减震设计

文献[8]基于隔震理论提出的减震结构优化设计方法，认为若采用黏性液体阻尼器，则当框架柱截面尺寸、混凝土强度确定时，求隔震层层高的问题可转化为求特征值问题。将框架结构底部2层设为隔震层，取隔震层固有频率等于场地特征频率，用Matlab编制简单程序可算出2个工程算例底部隔震层层高都在5 200 mm左右，在合理范围之内。

若防屈曲支撑布置在隔震层，则将使其抗侧刚度提高，不利于黏性液体阻尼器在多遇地震下更好地消耗能量，故建议防屈曲支撑布置在隔震层以上。图5所示为黏性液体阻尼器与防屈曲支撑在工程算例中的布置示意图。图4中，1号框架Y向，黏性液体阻尼器布置在①和④轴线；X向，黏性液体阻尼器布置在A和D轴线。2号框架Y向，黏性液体阻尼器布置在①，③，⑥和⑧轴线；X向，黏性液体阻尼器布置在A和D轴线。防屈曲支撑则布置在四角，芯材选Q235钢。

表1  框架柱配筋表

Table 1  Reinforcement in frame columns

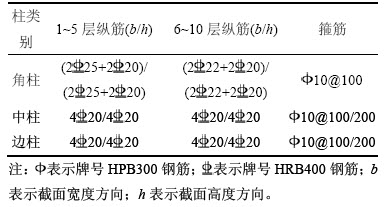
图4  框架结构平面示意图

Fig. 4  Diagrams of frame structure

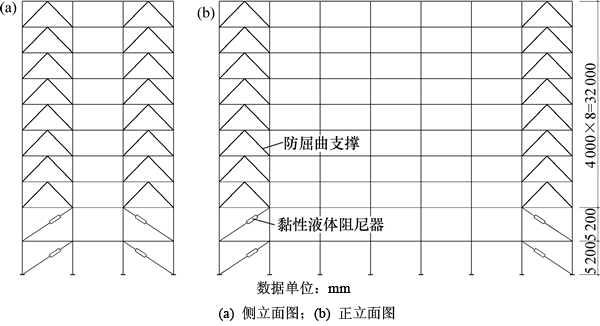
图5  防屈曲支撑与黏性液体阻尼器布置示意图

Fig. 5  Distribution diagrams of buckling-restrained braces and fluid dampers

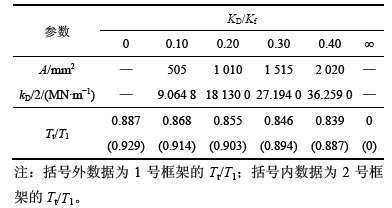
防屈曲支撑抗侧移刚度，以Y向1榀框架4根框架柱总抗侧移刚度K_f为参考，单支防屈曲支撑芯材面积为A、抗侧刚度为k_D/2，安装防屈曲支撑后结构扭转周期T_t与平动周期T₁比T_t/T₁见表2。表2中：K_D为1榀框架中所安装防屈曲支撑抗侧移刚度总和，K_D=2k_D。K_D/K_f=∞表示忽略偶然偏心的影响。

表2  抗侧刚度比K_D/K_f及相应平扭周期比T_t/T₁

Table 2  Lateral stiffness ratio K_D/K_f and corresponding translational-tortional period ratio T_t/T₁

3.3  分析与比较

安装防屈曲支撑提高框架减震结构的抗扭刚度后，消能效果需要通过时程分析进行验证。不失一般性，选取Elcentro地震记录S00E分量进行时程分析，如图6所示。多遇地震时，峰值加速度设定为110 cm/s²；罕遇地震时，峰值加速度设定为510 cm/s²。算例为2栋规则对称的框架结构，故本文仅对Y向输入地震波进行分析说明，并假定黏性液体阻尼器与防屈曲支撑与混凝土框架连接节点有足够的强度，在地震作用下不会发生屈服或者破坏。

3.3.1  弹性时程分析

为方便比较，针对1号和2号框架分别选择3种工况，见表3。表3中：C₁为安装在第1层单个阻尼器的阻尼系数；C₂为安装在第2层单个阻尼器的阻尼系数，阻尼指数取0.5。

图6  Elcentro地震记录

Fig. 6  Earthquake record of Elcentro

采用结构分析软件ETABS对2栋减震结构在多遇地震下进行时程分析，绘制最大层间位移角曲线如图7和图8所示。从图7和图8可见：

1) 若不考虑偶然偏心的影响，则在结构隔震层安装较小的阻尼器即可取得很好的消能减震效果，这表明偶然扭转使结构地震响应大大增加。

2) 当底部隔震层安装黏性液体阻尼器较少时，即使加大结构的抗扭刚度，消能减震效果仍有限(见图7(a)和图8(a))；而当底部隔震层安装黏性液体阻尼器适量时，加大结构的抗扭刚度，消能减震效果明显(见7(c)和图8(c))。

3) 考虑偶然偏心，将黏性液体阻尼器只安装在结构底部隔震层，当阻尼器适量时，多遇地震下亦能满足“小震不坏”的性能目标(见图7(c)和图8(c))，此时，底部隔震层的层间位移并非最大，因此，阻尼器耗能并非最佳，但对建筑空间的利用效率影响较小。

4) 从平扭周期比看，仅在框架结构四角安装防屈曲支撑提高抗扭刚度的效果有限，因而，其在多遇地震下的层间位移角曲线与忽略偶然偏心时层间位移角曲线呈现较大差异。

3.3.2  弹塑性时程分析

我国“建筑抗震设计规范”强调对消能减震结构应进行罕遇地震下的弹塑性变形验算^[10]，以确保“大震不倒”的性能目标。针对2号减震框架结构工况3，采用PERFORM-3D进行弹塑性时程分析，绘制不同抗侧刚度比K_D/K_f对应的最大层间位移角曲线，如图9所示。从图9可见：减震结构在罕遇地震下的最大层间位移角在第2层，小于1%，可确保实现“大震不倒”的性能目标；但最大层间位移角曲线并未因安装防屈曲支撑抗侧刚度增加而呈现与弹性时程分析相似的变化特征。这是因为进入弹塑性阶段后隔震层抗侧刚度将减小，但刚度呈不规律变化，故此时减震体系不再具有基础隔震体系的动力特性^[7]。其次是防屈曲支撑在减震体系中耗能非常小，低于1%。

表3  不同工况隔震层安装阻尼器阻尼系数

Table 3  Coefficient of dampers on isolation layer under different working conditions       MN·s·m^-1

图7  1号框架多遇地震下最大层间位移角曲线

Fig. 7  The maximum storey drift angle curves under frequently earthquakes of the 1st frame

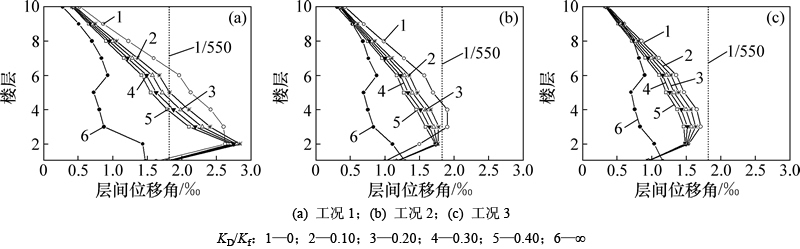
图8  2号框架多遇地震下最大层间位移角曲线

Fig. 8  The maximum storey drift angle curves under frequently earthquakes of the 2nd frame

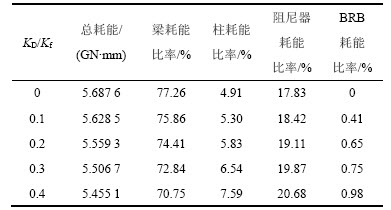
表4所示为减震体系各类型构件的总耗能以及梁、柱、阻尼器与防屈曲支撑耗能比率。从表4可见：尽管随着抗扭刚度增加，梁耗能比率有所下降，但仍然是最主要耗能组件；而阻尼器随着抗扭刚度加大，耗能比率有所增加，这与弹性阶段的类似，这也表明增加抗扭刚度减小偶然偏心的影响有利于黏性液体阻尼器的耗能。

图9  2号框架在罕遇地震下的最大层间位移角曲线

Fig. 9  The maximum storey drift angle curves under rarely earthquakes of the 2nd frame

表4  不同类型构件耗能总量以及各类型构件耗能比率

Table 4  Total dissipated energy of types of components and their dissipated energy ratios

4  结论

1) 偶然偏心使减震结构在地震作用下的响应大大增加。减震结构基于隔震理论优化设计方法必须考虑偶然偏心的不利影响。

2) 混合减震策略既可加大结构的抗扭刚度，又不影响隔震层内黏性液体阻尼器的消能能力。该策略所需消能部件少，可确保建筑空间的利用效率，且考虑了偶然偏心的不利影响，有较大的实用价值。

3) 算例中选用芯材为Q235的防屈曲支撑在弹塑性分析中耗能较小，其主要作用是提高抗扭刚度。若对减震结构的性能目标较高，则可选择低屈服点钢材作为防屈曲支撑芯材，以便消耗更多地震能量。

参考文献：

[1] Soong T T, Dargush G F. Passive energy dissipation systems in structural engineering[M]. New York: John Weley & Sons, 1997: 1-2.

[2] 周福霖. 工程结构减震控制[M]. 北京: 地震出版社, 1997: 1-12.

ZHOU Fulin. Vibration control for engineering structure[M]. Beijing: SeismologicalPress, 1997: 1-12.

[3] Yang J N, Lin S, Kim J H, et al. Optimal design of passive energy dissipation systems based on H_∞ and H₂ performances[J]. Earthquake Engineering & Structural Dynamics, 2002, 31(4): 921-936.

[4] Lavan O, Levy R. Optimal design of supplemental viscous dampers for irregular shear-frames in the presence of yielding[J]. Earthquake Engineering & Structural Dynamics, 2005, 34(8): 889-907.

[5] 李宏男, 曲激婷. 基于遗传算法的位移型与速度型阻尼器位置优化比较研究[J]. 计算力学学报, 2010, 27(2): 252-257.

LI Hongnan, QU Jiting. Comparison of optimal placement of displacement-based and velocity-based dampers using genetic algorithm[J]. Chinese Journal of Computational Mechanics, 2010, 27(2): 252-257.

[6] Attard T L. Controlling all unterstorey displacements in highly nonlinear steel buildings using optimal viscous damping[J]. Journal of Structural Engineering, 2007, 133(9): 1331-1340.

[7] Lavan O, Levy R. Simple iterative use of Lyapunov’s solution for the linear optimal seismic design of passive devices in framed buildings[J]. Journal of Earthquake Engineering, 2009, 13(5): 650-666.

[8] 陈敏, 贺国京, 刘畅, 等. 阻尼器在框架结构中的优化布置策略[J]. 土木建筑与环境工程, 2013, 35(4): 20-26.

CHEN Min, HE Guojing, LIU Chang, et al. An optimal distribution strategy for dampers in frame structures[J]. Journal of Civil, Architectural & Environmental Engineering, 2013, 35(4): 20-26.

[9] 陈敏, 刘畅, 邹银生. 新建减震结构优化设计方法[J]. 建筑科学与工程学报, 2015, 32(2): 65-70.

CHEN Min, LIU Chang, ZOU Yinsheng. A optimal design method for new energy dissipation structure[J]. Journal of Architecture and Civil Engineering, 2015, 32(2): 65-70..

[10] GB 50011—2010, 建筑抗震设计规范[S].

GB 50011—2010, Code for seismic design of buildings[S].

[11] 刘畅, 邹银生. 偶然偏心引起的结构地震扭转效应研究[J]. 工程抗震与加固改造, 2006, 28(3): 12-14.

LIU Chang, ZOU Yinsheng. Response of seismic torsional vibration induced by accidental eccentricity[J]. Earthquake Resistant Engineering and Retrofitting, 2006, 28(3): 12-14.

[12] 李宏男. 结构多维抗震理论[M]. 北京: 科学出版社, 2006: 68-78.

LI Hongnan. Earthquake resistant theory of structures to multi-dimensional excitations[M]. Beijing: Science Press, 2006: 68-78.

[13] Constantinon M C, Symans M D. Experimental study of seismic response of buildings with supplemental fluid dampers[J]. Structural Design of Tall Buildings, 1993, 2(2): 93-132.

[14] 周云. 防屈曲耗能支撑结构设计与应用[M]. 北京: 中国建筑工业出版社, 2007: 50-55.

ZHOU Yun. Structure design and application of buckling-resistant brace[M]. China Architecture & Building Press, 2007: 50-53.

[15] 李国强, 胡宝琳. 屈曲约束支撑滞回曲线模型和刚度方程的建立[J]. 地震工程与工程振动, 2007, 27(2): 26-31.

LI Guoqiang, HU Baolin. Establishment of hysteresis curve model and stiffness formula for buckling-restrained brace[J]. Journal of Earthquake Engineering and Engineering Vibration, 2007(2): 26-31.

[16] 赵瑛, 郭彦林. 防屈曲支撑框架设计方法研究[J]. 建筑结构, 2010, 40(1): 38-43.

ZHAO Ying, GUO Yanlin. Research on design method of buckling restrained braced frames[J]. Building Structure, 2010, 40(1): 38-43.

[17] JGJ 3—2010, 高层建筑混凝土结构技术规程[S].

JGJ 3—2010, Technical specification for concrete structures of tall building[S].

(编辑  陈灿华)

收稿日期：2015-02-10；修回日期：2015-04-20

基金项目(Foundation item)：国家自然科学基金资助项目(51178473)；湖南省教育厅科学研究青年基金资助项目(13B149)(Project (51178473) supported by the National Natural Science Foundation of China; Project (13B149) supported by the Research Fund of the Education Department of Hunan Province for Outstanding Youths)

通信作者：陈敏，博士，从事结构抗震减震研究；E-mail:chenmin2028@163.com