文章编号：1004-0609(2011)11-2896-07

基于松散耦合法的电磁管件胀形3D模拟

崔晓辉, 莫健华, 何文治

(华中科技大学 材料成形与模具技术国家重点实验室，武汉 430074)

摘  要：为了解决电磁管件胀形过程中磁场-结构场之间迭代耦合3D模拟的问题，采用ANSYS/EMAG得到不同时刻管件上的磁场力分布，并将节点力作为载荷输入到ANSYS/LS-DYNA进行管件动态塑性变形分析；然后将变形后的管件和空气网格输入到ANSYS/EMAG进行下一步的磁场分析。在管件变形过程中，对空气层网格采用任意拉格朗日算法，使空气网格能够随着管件的变形而有规则地变化，避免空气单元畸变。结果表明：管件外表面轴向中心点随时间位移值与实验结果基本一致；管件最终外表面轮廓与实验结果基本吻合；管件外表面轴向中心点位移与实验结果的误差为2.5%。

关键词：电磁成形；管件胀形；松散耦合法；有限元模拟；磁场力

中图分类号：TG391　     文献标志码：A

3D simulation of electromagnetic tube bulging based on loose coupling method

CUI Xiao-hui, MO Jian-hua, HE Wen-zhi

(State Key Laboratory of Material Processing and Die and Mould Technology,

Huazhong University of Science and Technology, Wuhan 430074, China)

Abstract: In order to overcome the magnetic-structure coupling problems in three-dimensional simulation of electromagnetic tube bulging, the ANSYS/EMAG was used to obtain the magnetic force on the tube at different times, and the magnetic force used as loading condition was imported into ANSYS/LS-DYNA to predict the dynamic deformation process on the tube. Then the deformed meshes of the tube and the air were imported into ANSYS/EANG to analyze the magnetic force on the tube. In the process of the tube deformation, the arbitrary Lagrangian-Eulerian algorithm was used in air mesh to make it change regularly with the deformation of the tube. This will avoid the air meshes distortion. The displacement at the center of the outer surface along the tube axis with time agrees with the experimental one. The final profile of the outer surface of the tube is in very good agreement with the measured one. The relative error of deflections at the center of the outer surface along the tube axis is 2.5%.

Key words: electromagnetic forming; tube bulging process; loose coupling method; numerical simulation; magnetic force

电磁脉冲成形是一种高能率成形方法。能量存储在电容中，放电开关瞬间闭合，工作线圈中就会有交变电流流过，产生强交变磁场，并穿透工件。根据趋肤效应，此磁场会在工件表面产生与线圈电流方向相反的感应电流，感应电流也会产生感应磁场，阻止线圈磁场穿透工件，从而使工件与线圈之间的磁场加强，并对工件产生强磁场力。工件就在磁场力的作用下发生高速变形。由于成形过程中线圈与工件没有接触，所以，工件表面不会出现压痕，使工件应变分布更均匀，能显著增加金属材料的成形极限。因此，电磁成形非常适合于铝合金等高电导率、难成形材料，是成形轻量化高强度材料的一种有效的技术手段^[1-3]。

电磁脉冲成形过程的研究大多采用实验的方   法^[4-5]。近10年由于有限元分析方法的发展和大型软件的推出，国内外学者开始使用软件耦合对电磁脉冲成形的作用进行研究。目前，采用的方法大多是利用电磁场分析模块模拟出磁场力的分布，再将磁场力作为边界条件输入到材料成形分析模块中进行模拟，研究工件与模具间冲击变形过程^[6]。

黄尚余等^[7]分析了板料电磁成形过程中成形载荷的计算方法。将载荷数值求解结果用于变形分析，成功预测了铝板的自由胀形过程。LEE等^[8]将磁矢量位引入到麦克斯韦方程组，采用无耦合法分析了电磁管件的胀形过程，有限元分析精度有一定的提高。IMBERT等^[9]采用AL-HASSANI^[4]得到了磁场力分布公式，采用无耦合法分析了板料和底模碰撞过程以及板料的破裂过程。研究表明，当板坯贴膜时，板坯经历了弯曲和矫直，这引起板坯既存在压缩弯曲应力，也存在拉伸应力。然而，他们的模拟方法均忽略了工件变形对磁场的影响。

于海平等^[10]采用数值模拟方法分析电磁缩颈过程，发现当工件变形量较大时，全耦合法模拟结果较半耦合法模拟结果更准确，而变形量较小时，两者的模拟结果接近，模拟结果与实验一致。CUI等^[11]采用顺序耦合法分析了电磁平板自由胀形过程，对板料周围的空气层单元采用网格重划分技术，实现了磁场-结构场间的迭代耦合分析，并得到最佳的计算时间子步以及变形过程中板料上磁场力的变化规律。认为如果忽略板料变形对磁场的影响，则会导致较大的磁场计算误差。YU和LI等^[12]采用顺序耦合法分析线圈长度对管件缩颈形状的影响，发现最大磁压力与管件的长度成正比，线圈长度增加使放电电流幅值变小，能量利用率降低，最终数值模拟得到的管件轮廓曲线结果与实验一致。为了减少3D电磁成形模拟的计算时间，UNGER等^[13]采用有效的实体-壳体公式和一个收敛条件进行磁场分析，实现了数据在磁场模块和结构变形模块的精确传递。OLIVEIRA等^[14]提出一种松散耦合法，采用3D电磁场模型和结构场模型共同分析平板电磁成形过程，合理地预测了工件变形和应变分布。

迄今为止，国外学者已逐步采用3D有限元模型分析电磁成形过程。然而，国内对电磁成形过程模拟都集中于2D轴对称模型。对于实际的工业应用，需要分析非轴对称和曲面复杂的成形零件，这都必须设计相应的3D有限元模型。因此，本文作者在OLIVEIRA等^[14]提出的松散耦合方法的基础上，对松散耦合法的相关技术进行了探索研究，并分析了3D电磁管件胀形过程。参照实验数据，验证模拟方法的正确性，为后续的研究开发一种有效的模拟技术。

1  模拟方法

基本方法是首先通过磁场分析软件ANSYS/ EMAG计算得到板料上各节点的洛伦兹力，然后将电磁力数据导入ANSYS/LS-DYNA分析板料的变形过程，再将变形后的工件几何数据导入ANSYS/EMAG进行下一磁场力分析。如此进行磁场与结构场交替分析，直到加载结束。其模拟分析流程如图1所示。

在该电磁力的模拟过程中，作为驱动源的模拟电流波形如图2所示^[15]，并将该电流分成10个时间段分别加载到ANSYS/EMAG模块中，计算磁场与电磁力。当用每个时间段的电流值计算出电磁力后，导入ANSYS/LS-DYNA模块， 根据材料本构方程对板材初始形状进行塑性成形分析，模拟出该时间段的材料变形，并更新工件成形过程中的形状数据，再将该数据返回导入ANSYS/EMAG模块，进行下一时间段的磁场分析与电磁力模拟。如此在磁场与结构场间耦合循环迭代分析直到加载时间结束。这种模拟过程即为考虑材料变形对电磁力影响乃至最终影响变形程度的松散耦合法。

图1  基于松散耦合法的模拟路线

Fig.1  Simulation flowchart of loose coupling method

图2  线圈中放电电流随时间的变化

Fig.2  Variation of discharged current flowing through coil with time

2  3D有限元模型的建立

为了与实际电磁成形数据进行比较，以验证所研究模拟方法的准确性，采用如图3所示的管件电磁胀形模型^[15]，根据图3所示的几何尺寸建立如图4所示的3D电磁场模型及管件、空气、线圈局部的网格划分(1/4模型)。在模拟电磁现象时，要考虑线圈和工件周围的空气，需建空气网格。为了提高计算的速度和精度，不能将空气网格划分为四面体形状，而须采用六面体形状，这增加了网格划分的难度。为了准确计算管件变形对磁场的影响，必须使空气网格随着管件的变形而变形。但是，对于六面体网格，随动过程中容易出错，导致单元畸变。因此，本文作者在计算管件塑性变形时，对空气单元采用任意拉格朗日欧拉算法(ALE)，并进行光顺处理，使空气网格随管件变形更规则。

图3  线圈与管件的2D几何模型

Fig.3  2D geometric model of coil and sheet (mm)

图4  3D有限元模型示意图

Fig.4  Schematic diagram of 3D finite element model

3  材料特性及条件

3.1  材料参数

根据文献[15]提供的管件电磁胀形的系统特性，本文作者采用如表1所示的线圈及材料参数。

3.2  塑性本构方程

采用显示分析模块ANSYS/LS-DYNA分析管件的电磁胀形过程，并采用如式(1)所示的本构方程^[15]。

                     (1)

式中：σ为真实应力；ε为真实塑性应变。

表1  管件电磁胀形的系统参数

Table 1  System parameters of electromagnetic tube bulging

4  模拟结果与分析

图5所示为变形终了时管件与空气层的网格变化。由图5可以看到，空气层区域的网格变形规则，空气的六面体网格随管件的网格变形而发生随动，没有出现单元的扭曲。因此，本文作者采用ALE算法能合理地描述空气网格随管件变形而变化的情况，进而保证管件上每个节点的磁场力数据和有限元模型在磁场-结构场之间精确传递，实现磁场-结构场间的真正3D迭代耦合仿真。

图5  空气与管件的网格最终变形图 

Fig.5  Final shape of mesh of tube and air

图6所示为变形终了时管件的3D塑性应变图。管件上的塑性应变整体分布很规则。这是由于管件是轴对称形状，空气网格采用规则的六面体单元，保证无论管件变形形状如何，其周围的空气层单元仍然进行着对称的变形，从而使管件周向每个节点的磁场力大小、变形量和应力应变分布在任意时刻均保持一致，确保了变形的均匀性和正确性。塑性应变区域主要集中于管件中部，管件端部的塑性应变几乎为0，这与线圈在管件上感应的磁场力分布有关。变形结束时，管件最大塑性应变为0.134 585。

图6  管件最终3D变形形状和塑性应变图

Fig.6  3D final shape and plastic strain of tube

图7所示为SUZUKI等^[15]的实验、模拟数据和本文模拟的数据做成的管件外壁中心节点在电磁胀形过程中变形位移与时间的关系曲线。本文作者采用的松散耦合法模拟得到管件中心节点随时间的位移量，在230 μs前的变化趋势与SUZUKI的实验数据几乎一致，在230 μs至300 μs之间的模拟值与SUZUKI的实验值一致。而SUZUKI的模拟结果在300 μs处与实验值差别较大。

图7  管件中心节点位移与时间的关系   

Fig.7  Radial displacement at center of tube with time

图8所示为SUZUKI等^[15]的实验数据、模拟数据和本文作者模拟的数据做成的管件外壁上各点经电磁胀形沿轴向分布的最终位置，横坐标的0处为管件外壁的中心部位。可以看出，本文作者松散耦合法模拟结果与SUZUKI的实验结果在管件的整体变形轮廓上基本吻合。变形结束后，模拟得到管件外壁中心节点的变形量为5.85 mm，SUZUKI的实验值约为6 mm，模拟误差仅为2.5%。 而SUZUKI的模拟结果与实验结果误差较大。根据图7和8可知，本文作者采用的松散耦合法模拟电磁成形的准确度很高。

图9所示为中心节点轴向速度和电流随时间的变化曲线。由图9可以看出，在123 μs时刻，管件中心节点变形速度最大值达到47 m/s。中心节点的速度曲线滞后于电流曲线。这说明惯性效应对成形起到一定的作用。

图10所示为不同时刻管件内壁节点速度矢量图。由图10可以看到，在240 μs之前，管件轴向位置(-76，-40)和(40, 76)之间节点的速度方向均指向管件中心。在0~240 μs之内，随着时间的延长，管件轴向(-40，40)间的节点速度方向越趋向于管件中心，并且速度大小不一致。因此，随时间的延长，管件最大变形量的区域面积逐渐减小。在250 μs之后，管件上节点的速度方向发生了改变。从图9可知，在250 μs以后，管件中心节点的速度大小呈现正负变化，这说明此时管件发生回弹现象。在300 μs时刻，管件拐角处的节点速度小于其他区域的速度。

图8 计算和实验下的管件最终变形轮廓

Fig.8  Calculated and experimental final deformation profiles

图9  管件中心节点速度和电流随时间的变化曲线

Fig.9  Variation of radial velocity and current at center of tube with time

图10  不同时刻管件内壁节点速度

Fig.10  Change of velocity of tube at different times: (a) t=52.5 μs; (b) t= 105 μs; (c) t=157.5 μs; (d) t= 300 μs

图11所示为不同时刻管件的变形轮廓。当变形终了时，在管件轴向坐标(60，76)和(-76，60)的区域内，管件的径向位移为负值，其中，在轴线64 mm的位置处，其变形量为-0.069 mm。这是因为在250 μs后，管件上的节点速度方向会发生变化，并且管件拐角处的节点速度小于其他区域的，阻碍了端部材料向管件中心的流动，引起管件端部出现轻微的起皱现象。

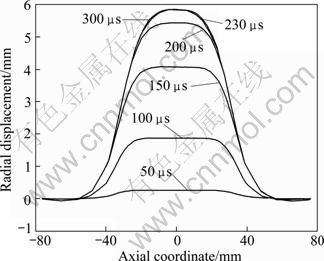
图11  不同时刻管件的变形轮廓

Fig.11  Tube deformation profiles at different times

5  结论

1) 采用ANSYS/EMAG求解不同时刻管件上的磁场力，采用ANSYS/LS-DYNA求解管件的动态变形过程。将管件周围的空气层划分为六面体单元，并对空气场采用任意拉格朗日算法，使空气网格随管件的变形而规则变形。从而确保管件上每个节点力及有限元模型在磁场-结构场之间精确传递，实现磁场-结构场间的迭代耦合3D模拟分析。模拟结果与实验结果一致。

2) 管件中心节点速度曲线滞后于电流曲线，说明惯性效应对成形起到一定作用。250 μs后速度曲线呈现正负交替现象，说明此刻管件发生了一定的回弹。

3) 管件端部节点的速度指向管件中部，致使管件在轴向上缩短。在250 μs后，管件上节点的速度矢量方向发生变化，尤其是管件拐角处的节点速度小于其他区域的，阻碍了管件端部材料向中心的流动，引起管件端部出现轻微的起皱现象。

4) 建立的3D模拟算法可应用于非轴对称工件的成形模拟以及复杂结构线圈的磁场力分析。工业中3D复杂形状工件的电磁成形应用提供了一种可靠的模拟途径。

REFERENCES

[1] 韩 飞, 莫健华, 黄树槐. 电磁成形技术理论与应用的研究进展[J]. 锻压技术, 2006, 31(6): 4-8.
HAN Fei, MO Jian-hua, HUANG Shu-huai. Theoretical study and application of electromagnetic forming technology[J]. Forging & Stamping Technology, 2006, 31(6): 4-8.

[2] American Society for Metals. ASM handbook (volume 14): Forming and forging[M]. Ohio: ASM International Handbook Committee, 1988: 1420-1425.

[3] THOMAS J D, SETH M, DAEHN G S, BRADLEY J R, TRIANTAFYLLIDIS N. Forming limits for electromagnetically expanded aluminum alloy tubes: Theory and experiment[J]. Acta Materialia, 2007, 55(8): 2863-2873.

[4] AL-HASSANI S T S. Magnetic pressure distribution in the sheet metal forming[C]//Electrical Methods of Machining, Forming and Coating, Institute of Electrical Engineering Conference, 1975: 1-10.

[5] TAKATSU N, KATO M, KEIJIN S, TOSHIMI T. High-speed forming of metal sheets by electromagnetic force[J]. Japan Society of Mechanical Engineers International Journal: Series Ⅲ, 1988, 31(1): 142-148.

[6] CORREIA J P M, SIDDIQUI M A, AHZI S, BELOUSTTAR S, DAVIES R. A simple model to simulate electromagnetic sheet free bulging process[J]. International Journal of Mechanical Sciences, 2008, 50(10/11): 1466-1475.

[7] 黄尚宇, 常志华, 王立峰, 吴莉花, 张 猛, 姜奎华. 板坯电磁成形载荷计算方法及分布特性[J]. 中国有色金属学报, 1998, 8(3): 441-446.
HUANG Shang-yu, CHANG Zhi-hua, WANG Li-feng, WU Li-hua, ZHANG Meng, JIANG Kui-hua. Calculation and distribution of forming load for sheet metal magnetic forming[J]. The Chinese Journal of Nonferrous Metals, 1998, 8(3): 441-446.

[8] LEE S H, LEE D N. A finite element analysis of electromagnetic forming for the tube expansion[J]. Journal of Engineering Materials and Technology, 1994, 116(2): 250-254.

[9] IMBERT J M, WRINKLER S L, WORSWICK M J, OLIVEIRA D A, GOLOVASHCHENKO S. The effect of tool-sheet interaction on damage evolution in electromagnetic forming of aluminum alloy sheet[J]. Journal of Engineering Materials and Technology, 2005, 127(1): 145-153.

[10] 于海平, 李春峰, 李 忠. 基于FEM的电磁缩颈耦合场数值模拟[J]. 机械工程学报, 2006, 42(7): 231-234.
YU Hai-ping, LI Chun-feng, LI Zhong. Numerical simulation of coupled fields of electromagnetic forming for tube compression based on FEM[J]. Chinese Journal of Mechanical Engineering, 2006, 42(7): 231-234.

[11] CUI Xiao-hui, MO Jian-hua, XIAO Shi-jie, DU Er-hu, ZHAO Jian. Numerical simulation of electromagnetic sheet bulging based on FEM[J]. The International Journal of Advanced Manufacturing Technology, 2011, 57(1/4): 127-134.

[12] YU Hai-ping, LI Chun-feng. Effects of coil length on tube compression in electromagnetic forming[J]. Transactions of Nonferrous Metals Society of China, 2007, 17(6): 1270-1275.

[13] UNGER J, STIEMER M, SCHWARZE M, SVENDSEN B, BLUM H, REESE S. Strategies for 3D simulation of electromagnetic forming process[J]. Journal of Materials Processing Technology, 2008, 199(1/3): 341-362.

[14] OLIVEIRA D A, WORSWICK M J, FINN M, NEWMAN D. Electromagnetic forming of aluminum alloy sheet: Free-form and cavity fill experiments and model[J]. Journal of Materials Processing Technology, 2005, 170(1/2): 350-362.

[15] SUZUKI H, NEGISHI H, YOKOCHI Y. Free expansion of tube under magnetic pressure[J]. Journal of the Japanese Society for Technology of Plasticity, 1986, 27: 1254-1260.

(编辑 龙怀中)

基金项目：国家自然科学基金资助项目(50875093)

收稿日期：2010-11-18；修订日期：2011-03-25

通信作者：莫健华，教授，博士；电话：13477081759；E-mail：mjh@mail.hust.edu.cn