J. Cent. South Univ. Technol. (2009) 16: 1028-1033
DOI: 10.1007/s11771-009-0170-8

Discrete element simulation of mechanical characteristic of
conditioned sands in earth pressure balance shield tunneling
WU Li(武 力), QU Fu-zheng(屈福政)
(School of Mechanical Engineering, Dalian University of Technology, Dalian 116024, China)
Abstract: The discrete element method (DEM) was used to simulate the flow characteristic and strength characteristic of the conditioned sands in the earth pressure balance (EPB) tunneling. In the laboratory the conditioned sands were reproduced and the slump test and the direct shear test of the conditioned sands were implemented. A DEM equivalent model that can simulate the macro mechanical characteristic of the conditioned sands was proposed, and the corresponding numerical models of the slump test and the shear test were established. By selecting proper DEM model parameters, the errors of the slump values between the simulation results and the test results are in the range of 10.3%-14.3%, and the error of the curves between the shear displacement and the shear stress calculated with the DEM simulation is 4.68%-16.5% compared with that of the laboratory direct shear test. This illustrates that the proposed DEM equivalent model can approximately simulate the mechanical characteristics of the conditioned sands, which provides the basis for further simulation of the interaction between the conditioned soil and the chamber pressure system of the EPB machine.
Key words: conditioned sands; slump test; direct shear test; discrete element simulation; earth pressure balance shield machine
1 Introduction
The earth pressure balance (EPB) shield machine is the most common mechanized tunneling equipment, because it has been successfully adopted in underground excavation under very different ground conditions for many years. Under unfavorable geological conditions, e.g. coarse sand ground, additives (mainly foams and polymers) should be injected into the buck chamber ahead of the cutting wheel in order to condition the ground[1]. Due to the additives, the features of the conditioned sands are different from those of the original sands. The conditioned sand is a kind of liquid-solid material, which should have the features of low inner friction, good plasticity and low penetrability[2]. The slump test[2-4] and the direct shear test/triaxial test[3] are the common methods to test the flow property and shear strength property of the conditioned sands. QUEBAUD et al[2] suggested that the slump of 12 cm was the best for the conditioned sand transmission as well as the chamber pressure control. VINAI et al[3] recommended that the range of the slump of the conditioned sands was 120-225 mm, and PSOMAS[4] presented that the friction angle of the conditioned fine sand was less than 25? and that of the conditioned coarse sand was less than 30?.
The key for tunneling safely and rapidly is the pressure balance control between the buck chamber and the ground at the excavation face. The numerical simulation is considered as a necessary tool to solve the problem. Compared with the finite element method, the discrete element method (DEM) can reproduce the dynamic work process of the machine, which has been widely used in the simulation of the interaction between soils and machine structure[5-8], so the DEM has the potential advantage in modeling the buck transmission process of the chamber pressure system of the shield machine. To simulate the interaction between the conditioned sands and the system, the primary task is the simulation of the conditioned sand, that is, the establishment of the DEM model of the conditioned sands. Usually, the DEM model of materials is testified by the macro property test results. For example, the cone penetration test was used to verify the DEM model of soils[9-11], the direct shear test was used to verify the DEM model of manure product[12], the compression test was adopted to verify the DEM model of asphalt concrete[13], and the plane strain test was used to check the DEM model of sands[14]. Few researches on the DEM model of the conditioned sands and the property test simulation have been found so far.
In this work, the conditioned sands were reproduced in the laboratory. By comparing the simulation results of the slump tests and the shear tests of the conditioned sands with those of the real tests, the feasibility of the DEM model to simulate the mechanical behavior of the conditioned sands was discussed.
2 Characteristic tests of conditioned sands
2.1 Production of conditioned sands
The conditioned sand of EPB shield machine was a kind of multi-phase material composed of sand particles, water and additives. The additives included the foam and bentonite slurry. The mechanical property of the conditioned sands changed with the variation of the content of the water and additives. In the laboratory, three kinds of conditioned sands with different additive contents were reproduced.
2.1.1 Original sand
The original sand came from a section of a railway. The particle grading of it is shown in Table 1. The water content (in mass fraction) was between 4.6% and 20.4%. The average natural density was 1.79 g/cm3. The original sand was washed and then dried in the oven. Some of the dried sand particles were directly used to reproduce the conditioned sands in the slump test, some were sieved through the 5# hole and then used to reproduce the conditioned sands in the direct shear test.
Table 1 Particle grading of original sands

2.1.2 Foam
The function of foam was to reduce the surface contact tension of the soil particles, weaken the connected force of water between soil particles and lubricate the soil. The foam was generated by impacting 5% foaming agent solution at a high pressure air of 0.2 MPa. The expand ratio (the ratio of the measured volume of foam to the volume of the liquid required for its production) and the drainage time (the time required to drain out 50% volume of the foam) of the foam was 27 and 20 min, respectively. Because the foam property depended on the time, the produced foam should be put into the reproduced sand immediately.
2.1.3 Bentonite slurry
The role of the bentonite powder was to fill the theoretical porosity of the sand and create the impermeable ‘filter cake’ during tunneling. The powder was also able to enhance the cohesion of the conditioned sands. The bentonite powder and water were mixed to produce the slurry with the content of 30%, which should be used after 24 h.
Supposing that the additives were put among the sand particles, that was, the sample volume of the conditioned sand was equal to that of the excavated sands, and the ratio of the volume of the excavated sands to that of the original sands was 1.3?1.0. Referring to the practical tunneling of EPB machine, the volume of the additives was calculated according to the volume of the original sand. The parameters of conditioned sands with three ratios are listed in Table 2.
Table 2 Parameters of conditioned sands
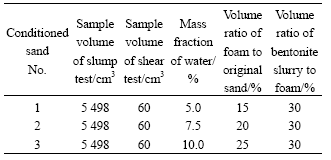
2.2 Slump test of conditioned sands
The container adopted in the slump test was a truncated cone with an upper diameter of 100 mm, a bottom diameter of 200 mm and a height of 300 mm. According to the standard test operations[15], the conditioned sands were put into the container. Then the container was lifted vertically and the conditioned sands flowed under the gravity. The slump of the conditioned sands was measured. For each kind of conditioned sand, the same test was repeated three times. The average slump of each kind of conditioned sands is shown in Table 3. The final slumped shapes of the conditioned sands are shown in Fig.1.
Table 3 Comparison of simulation results and test results of slump


Fig.1 Final shapes of conditioned sands in slump test: (a) Conditioned sands 1; (b) Conditioned sands 2; (c) Conditioned sand 3
2.3 Direct shear test of conditioned sands
The conditioned sands were put into the shear box with an area of 30 cm2 and a height of 2 cm. The vertical load grades (25, 50, 75 and 100 kPa) were adopted in the rapid shear test. For each kind of conditioned sands, the same test was repeated three times. The curves between the shear stress and the shear displacement under four different vertical loads were obtained. For each kind of conditioned sands, the linear regression results of the maximum shear stress vs the vertical load are shown in Fig.2.

Fig.2 Relationship between maximum shear stress and vertical stress of conditioned sands
3 DEM model of conditioned sands
The modeling idea of the DEM model of the conditioned sands was described as follows. The material of the conditioned sands was partitioned by a series of uniform particle elements with the random arrangement. The particle element did not represent the microstructure of the sand particles, but a micro structural model in its own right. The particle elements contacted with each other and the contact model was defined. The contact model parameters were determined by try and error method. When the predictions of the numerical model agreed with the observed data of the property tests, the accuracy of the models increased. This DEM model of the conditioned sands was actually an equivalent computation model, which could not only simulate the large strain and flow behavior of the conditioned sands conveniently, but also enhance the computation efficiency.
The contact model of the conditioned sands was the combination of the linear stiffness model, the contact bond model and the slip model (see Fig.3).
The linear stiffness model provided an elastic relationship between contact force and relative displacement, which was used to simulate the elastic property of the conditioned sands. The contact bond model limited the normal and shear bond strength. It was used to simulate the viscous interaction force of the foam and the bentonite powder between sand particles. When the tangential contact force exceeded the maximum slip

Fig.3 Contact model of conditioned sands (m1 and m2 are particles)
friction force, the particles would slip. It was used to simulate the plastic law of the conditioned sands. The normal and tangential contact forces between particles are shown as follows:
≥
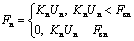 (1)
(1)
where Fn is the force in the normal direction of the contact plane; Kn is the normal contact stiffness; Un is the displacement in the normal direction of the contact coordinate system (Un>0 indicates overlap); and Fcn is the contact bond strength in the normal direction.
≥
<
 (2)
(2)
where Fs is the tangential force; Ks is the tangential contact stiffness; ΔUs is the displacement increment in the tangential direction of the contact coordinate system; Fcs is the contact bond strength in the tangential direction; and fu is the friction coefficient.
4 DEM simulation of mechanical characteri- stic test of conditioned sands
4.1 DEM simulation of slump test
4.1.1 Simulation process of slump test
The simulation process was described as follows.
(1) According to the dimension of the cone used in the laboratory slump test, a virtual container composed of a cylinder wall element and two-plane wall elements was established.
(2) The particles were generated in the container randomly with a porosity of 0.45. According to the proportion of the geometry size to the particle element size[6], the radius of the particle (5 mm) was selected. The contact stiffness and density (2.637 g/cm3) were added to the particles. Calculation was implemented until reaching the balance state of system. The DEM contact model parameters of three kinds of conditioned sands, which were determined by the macro measured results of the slump test, are listed in Table 4.
(3) In order to ensure the installation of the contact bond model, the floating particle elimination arithmetic[16] was introduced to realize that each particle contacts with more than two particles. The arithmetic is presented in Fig.4, where Fa is the mean contact force for the assembly; Nc is the contact number of the particles; FP is the average contact force for each particle; R[F] is
Table 4 DEM model parameters of conditioned sands in slump test simulation
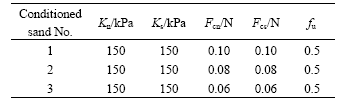

Fig.4 Diagram of floaters eliminating arithmetic
the radius of floaters; fu[F] is the friction of the floaters; R[AF] is the radius of the active floaters; and Fp[AF] is the average contact force for each active floater.
(4) The bond model was added to the particle contact and the gravity was forced to the particle collection. Calculation was implemented until reaching the balance state of the particle collection.
(5) The cylinder wall element was moved upward at a speed of 0.5 m/s and the particle collection flowed under the gravity. When the simulation time reached 4 s and the kinetic energy of the particle collection was stable, the calculation was stopped.
(6) The distance from the highest particle of the collection to the bottom plane was calculated.
4.1.2 Result analysis of slump test simulation
The simulation results of the slump test are shown in Fig.5, and the slumps are compared with the test results and shown in Table 3.

Fig.5 DEM simulation results of slump test: (a) Initial model; (b) Conditioned sands 1; (c) Conditioned sands 2; (d) Conditioned sands 3
By comparing the simulation results of the slump test (Fig.5) with the test results (Fig.1), and studying the model parameters (Table 1) and results of the slump (Table 3), the following conclusions are drawn.
(1) From the final slumped shape, the simulation results of the slump test of the conditioned sands with three kinds of proportions well agree with the test results. From the slump, the error of simulation results and the test results is not more than 14.3%.
(2) The final slumped state and slump of the conditioned sands are controlled by the parameter of the contact bond strength in the DEM simulation. Under the same contact stiffness and friction, the higher the bond strength, the smaller the simulation result of the slump.
(3) The higher the contents of water and foam in the conditioned sand are, the larger the slump is; in DEM simulation, the lower the bond strength is, the larger the simulation result of the slump. So the bond strength is inversely proportional to the contents of the foam and water in the conditioned sands.
(4) The influence of the contact bond strength on the simulation results of the slump test is described as follows. In the initial model, the particles connect with each other, so under the gravity, the movement of the particle collection is continuous. With the increase of the simulation time, the bottom particles become dense, and the contact forces increase. If the bond strength is set too low, the contact force between particles will exceed the bond strength, which leads to the bond break, the movement of the particle collection incompatible continuum, and then the increase of slump. The contact bonds of the DEM model of the conditioned sands with three ratios are shown in the simulation results (thin line in Fig.5).
4.2 DEM simulation of direct shear test
4.2.1 Simulation process of direct shear test
The model of the shear test is shown in Fig.6. The simulation process is as follows.
(1) According to the dimension of the shear box used in the laboratory test, a virtual container was established. The container consisted of two separate parts so that it allows the level shear movement of the sample. Each part was composed of a cylinder wall element and a plane element.
(2) According to the ratio of the geometry size to the particle element size[6], the diameter of the particle (2 mm) was selected. The DEM contact model parameters of three kinds of conditioned sands, which were determined by the measured results of the direct shear test, are shown in Table 5. Other settings are the same as those in the slump test simulation.
(3) The normal loading stress was applied to the sample via the upper plane wall element. After the samples reached equilibrium, the shear movement of the lower part was initiated until the opposite displacement of the two parts reached 6 mm.
(4) During the calculation cycling, the shear displacement that was the product of the shear velocity and the calculation time, and the shear stress which was calculated by the average normal stress of the cylinder

Fig.6 DEM model of direct shear test of conditioned sands: (a) Initial state; (b) Final state; (c) 3D view of initial state
Table 5 DEM model parameters of conditioned sands in direct shear test simulation

wall were recorded.
4.2.2 Result analysis of direct shear test simulation
The simulation curves and the test curves of the direct shear tests are shown in Fig.7. The lines with hollow dots represent simulation curves. The lines with hard dots represent test curves. As seen from Fig.7, Tables 1 and 5, the following conclusions can be drawn.
(1) Compared with the test curves, the simulation curves have larger fluctuation because the particle size is large. Once a particle is extruded away from the shear plane, the shear stress will drop abruptly. If the grain size

Fig.7 Comparison of simulation curves with test curves of different conditioned sands: (a) Conditioned sands 1; (b) Conditioned sands 2; (c) Conditioned sands 3
gradient is adopted, the curve fluctuation will be reduced.
(2) Under the same vertical load, the simulation curve is mainly controlled by the contact model parameters of the contact stiffness and friction coefficient. The larger the contact stiffness and the friction coefficient are, the larger the shear stress at the same shear displacement is.
(3) Under different vertical loads, the simulation curves calculated by the same set of the contact model parameters are identical to the test curves; by setting different sets of contact model parameters, the simulation curves well agree with the test curves of the three kinds of the conditioned sands.
(4) In order to quantitatively analyze the similarity, the relative error of the simulation curves and the test curves is defined as Eq.(3), and the errors are shown in Table 6.
 (3)
(3)
where xi(=0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0, 5.5, 6.0 mm) is the shear displacement; y(xi) is the simulation result of shear stress; and τ(xi) is the test result of shear stress.
Table 6 Relative errors of simulation curves and test curves (%)

The relative errors of the simulation curves and the test curves is between 4.68%-16.5%, which illustrates that if the parameters are selected correctly, the DEM equivalent model can simulate the mechanical property of the conditioned sands.
5 Conclusions
(1) In DEM simulation, the higher the contact bond strength, the smaller the simulation result of the slump. The larger the contact stiffness and the friction coefficient are, the larger the shear stress at the same shear displacement is.
(2) By setting the contact model parameters, the errors of the slump of three kinds of conditioned sands are between 10.3% and 14.3%, and the simulation results of the slumped shape of the conditioned sands well agree with the experiment results. The relative error range of the simulation curves and the test curves of the direct shear test of the three kinds of conditioned sands is 4.68%-16.5%, which proves that the proposed DEM model is feasible to simulate the mechanical property of the conditioned sands.
References
[1] PEILA D, OGGERI C, VINAI R. Screw conveyor device for laboratory tests on conditioned soil for EPB tunneling operations[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133(12): 1622-1625.
[2] QUEBAUD S, SIBAI M, HENRY J P. Use of chemical foam for improvements in drilling by earth pressure balanced shields in granular soils[J]. Tunnelling and Underground Space Technology, 1998, 13(2): 173-180.
[3] VINAI R, OGGERI C, PEILA D. Soil conditioning of sand for EPB applications: A laboratory research[J]. Tunnelling and Underground Space Technology, 2008, 23(3): 308-317.
[4] PSOMAS S. Properties of foam/sand mixtures for tunneling applications[D]. Michaelmas: University of Oxford, 2001.
[5] NEZAMI E G, HASHASH Y M A, ZHAO D W, GHABOUSSI J. Simulation of front end loader bucket-soil interaction[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2007, 31(9): 1147-1162.
[6] MELIS-MAYNAR M J, MEDINA-RODRIGUEZ L E. Discrete numerical model for analysis of earth pressure balance tunnel excavation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(10): 1234-1242.
[7] HOMER D A, PETERS J F, CARRILLO A. Large scale discrete element method modeling of vehicle-soil interaction[J]. Journal of Engineering Mechanics, 2001, 127(10): 1027-1032.
[8] FRANCO Y, RUBINSTEIN D, SHMULEVICH I. Prediction of soil-bulldozer blade interaction using discrete element method[J]. Transactions of the ASABE, 2007, 50(2): 345-353.
[9] ZHOU Jian, CUI Ji-hong, JIA Min-cai, SHI Dan-da. Numerical simulation of cone penetration test by discrete element method[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(11): 1604-1610.(in Chinese)
[10] TANAKA H, MOMOZU M, OIDA A, YAMAZAKI M. Simulation of soil deformation and resistance at bar penetration by the distinct element method[J]. Journal of Terramechanics, 2000, 37(1): 41-56.
[11] ASAF Z, RUBINSTEIN D, SHMULEVICH I. Determination of discrete element model parameters required for soil tillage[J]. Soil and Tillage Research, 2007, 92(1/2): 227-242.
[12] LANDRY H, LAGUE C, ROBERGE M. Discrete element representation of manure products[J]. Computers and Electronics in Agriculture, 2006, 51(1/2): 17-34.
[13] KIM H, WAGONER M P, BUTTLAR W G. Simulation of fracture behavior in asphalt concrete using a heterogeneous cohesive zone discrete element model[J]. Journal of Materials in Civil Engineering, 2008, 20(8): 552-563.
[14] ZHOU Jian, SU Yan, CHI Yong. Simulation of soil properties by particle flow code[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(3): 390-396. (in Chinese)
[15] DANIEL D G, LOBO C L. User’s guide to ASTM specification C 94 on ready-mixed concrete: (MNL 49)[M]. New York: ASTM International, 2005.
[16] CUNDALL P A. PFC3D user’s manual[M]. Minneapolis: Itasca Consulting Group Inc, 2005: 395-397.
(Edited by CHEN Wei-ping)
Foundation item: Project (2007CB714006) supported by the National Basic Research Program of China
Received date: 2009-01-13; Accepted date: 2009-04-17
Corresponding author: WU Li, Doctoral candidate, Tel: +86-13504110642; E-mail: jlwuli2004@yahoo.com.cn