J. Cent. South Univ. (2017) 24: 819-828

DOI: 10.1007/s11771-017-3484-y

An adaptive stable observer for on board auxiliary inverters with online current identification strategy

LI Wei(李蔚)^{1, 2, 3}, LIU You-mei(刘友梅)², CHEN Te-fang(陈特放)^{1, 3}, DENG Jiang-ming(邓江明)²

1. School of Information Science and Engineering, Central South University, Changsha 410083, China;

2. Zhuzhou Electric Locomotive Limited Company, CRRC, Zhuzhou 412001, China;

3. School of Traffic Transportation Engineering, Central South University, Changsha 410075, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2017

Abstract: An adaptive stable observer with output current online identification strategy for the auxiliary inverters applied in advanced electric trains, such as high speed railway, urban rail, subway and maglev trains, is proposed. The designed observer is used to estimate the state variables, i.e. controllable duty ratio and current components in d-q-o rotary reference frame. The convergence of the observer estimation error is analyzed with consideration of uncertain level variation of input voltage at direct current (DC) side and sufficient conditions are given to prove its practical stability. Experimental results are shown to confirm the effectiveness of the proposed observer.

Key words: auxiliary inverter; adaptive observer; online identification; Lyapunov function; parameter variation

1 Introduction

In general, auxiliary inverters are considered as basic building blocks and key components in various industrial applications, such as power supplies, machine driving, and renewable energy systems, etc [1-3]. The high and continuous interest in employing auxiliary inverters has been specially motivated by the ability of inverters to provide good performance of voltage and frequency control in a single power stage. Auxiliary inverters, which primarily provide the stable three-phase four-wire sinusoidal voltage power supply with 380 V/ 50 Hz for AC loads in trains such as air conditionings, ventilators, lightings and electric heaters, are essential electrical equipments in electrical trains such as subway, urban railway and maglev train [4]. Moreover, the working environment of the on board auxiliary inverter has two noticeable characteristics: the input bus voltage fluctuating from 1200 V to 1800 V and the loads possibly nonlinear and suddenly switched. However, the power system must meet basic requirements as follows:

1) Steady output voltage (AC 380V) and low harmonic (THD <8%);

2) The ability to resist the affection of sudden changeability of the loads and bus voltage instability;

3) The fluctuation amplitude is less than 15%, and output voltage must return to normal value within the required time (usually 100-200 ms) [5].

In order to meet above industrial demands, intensive studies are being conducted to develop some modulation techniques which are capable of optimizing the performance of inverters. For instance, bus voltage feed-forward control to overcome the influence of bus voltage fluctuation is introduced in Ref. [6]. To enhance the adaptiveness of auxiliary inverter system under changeable work environment and to ensure its strictly sinusoidal output waveform stably, an adaptive fuzzy control with three closed-loop is mentioned in Ref. [7].

Taking the existing and related achievements into consideration, PID scheme [8], repetitive control [9, 10], Deadbeat control [11], H_∞ theory [12], resonant controller [13, 14] have been also applied in auxiliary inverter. PID scheme has merits of simple realization and shortcoming of limited harmonic suppression capability. Repetitive control has a merit of theoretically full-band harmonic suppression capability, but its stability is questionable. Deadbeat control which is specially designed for digital system, has the merits of one beat delay tracking reference signal and the shortcoming of limited harmonic voltage suppression capability as well as H∞ theory. Because of infinite gain in resonant frequency, resonant controller is capable of suppressing harmonics and voltage unbalances. However, complicated realization and existence of digital control delay [15, 16] and discrete coupling [17] typically lead high-order resonant controller to unstable characteristic.

It is well known that an effective method, named state-space averaging modulation [18], can be applied to illustrate the dynamic behaviour of three-phase dc-ac converters in synchronous-reference frame [19].

Consequently, in this paper, a novel adaptive stable observer designed for the auxiliary inverter is proposed to estimate the state current, voltage variation of DC side, and duty ratio output variable by using only the measurable output voltages. On the basis of double-loop SVPWM controlling method with PI controller in d-q coordinate system, the observer has been finally tested and verified its reasonability and practicability in industrial application.

2 Mathematical model of auxiliary inverter

Considering the typical construction of auxiliary inverter, as shown in Fig. 1, the three-phase load can be regarded as impedance circuit, using Z to represent, which follows by the alternating current (AC) filter. The function of capacitor board is to hold the input direct current (DC) voltage stably. In Fig. 1, u_dc represents the input DC voltage, u_i(i=a,b,c) represents corresponding phase to phase voltage of each branch from insulated gate bipolar translator (IGBT) arrays, and L, C are inductance and capacitance respectively of AC filter.

Fig. 1 Structure of auxiliary inverter

As can be seen from Fig. 1, the average switching cycle model of the input and output state equations can be written as follows:

            (1)

where the line to line ouput voltage vector u_L-L=[u_AB u_BC u_CA]^T , the line to line inductance current vector l_l-l=[l_ab l_bc l_ca]^T , the line to line duty ratio vector d_l-l=[d_ab d_bc d_ca]^T, T_s is switching period, and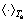represents switching cycle average value.

The relationship between DC-side average current and is illustrated by

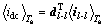                           (2)

By changing the corresponding vectors G (G =u, l, d) from the three-phase stationary reference frame (abc frame) to two-phase rotary reference frame (d-q-o frame), the following transforming relationship is shown as

                               (3)

and the transforming matrix is

     (4)

where w is the rotating velocity and the coefficients 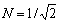and k=2p/3.

The dynamical representation of the inverter, in the synchronous (d-q-o)-reference frame, can be extended from Eq. (1) as

 (5)

where the vector G _d-q-o includes d-axis component G_d and q-axis component G_q.

In addition, the relationship between DC-side average current and (d-q-o)-reference frame current vector is then

                        (6)

If the three-phase output is supposed to be strictly balanced, one may get and Then, by ignoring the o-axis components in Eq. (5), one can further get

   (7)

Note that the number of dimensions in Eq. (5) has been reduced from three to two.

3 Adaptive stable observer design for auxiliary inverter

In this section, the main design process of the adaptive stable observer for auxiliary inverter is represented.

3.1 Modelling of adaptive observer

Choose proper state vector x and input vector z as that

,

Then, the differential equations in Eq. (7) can be easily expressed as

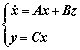                               (8)

where the coefficient matrixes are

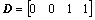
           (9)

In order to obtain the dynamics of state and output variables, one can establish the adaptive observer, i.e.,

                       (10)

where G is the observing gain matrix, ^ is the estimated value of corresponding variable.

Let 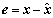, then combining Eqs. (8) and (10), yields

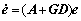                              (11)

The above equation indicates the first-order differentiation of estimated error. Consequently, consider the following candidate Lyapunov function:

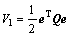                                (12)

where the designed parameter Q is positive.

After taking derivative of V₁, Eq. (12) becomes

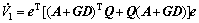            (13)

For the purpose that the estimation value of x or y can gradually trace its actual value, the following condition should satisfy

                (14)

Only the above inequality is satisfied, we may have

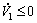                                     (15)

3.2 Stability analysis of observer under uncertain parameters

As a rule, the input or feedback control parameters may vary. Then, the inverter is subject to uncertainty, which affects the dynamical behavior. In this section, we analyze the robustness of the observer under the presence parametric uncertainty. To achieve this, some concepts and definitions of the practical stability are given. It is clear that the practical stability is more suitable in dealing with concrete problems of the real world (see Ref. [20] for more details). In the sequel, we assume that the parameters of inverter are uncertain but with actually bounded values, and this precondition is reasonable and also it will be further discussed later.

There is no doubt that the connected parameters are invariable in any control period, i.e.,

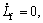
                      (16)

Then, consider the system under parametric uncertainties represented in the following form:

                (17)

The above equation illustrates the variation of rotating velocity w. Actually, the DC-side power source directly connecting to supporting capacitor may leads to obvious voltage change, i.e.,

            (18)

Since the parameters of inverter are uncertain but with actually bounded values, there exists a positive constant c_i>0, for i=1, 2, such that

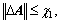
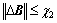                        (19)

where parameters c_i>0, i=1, 2, are positive constants determined from the maximal values of DA and DB in physical domain. Then, Eq. (8) may be written as

                    (20)

Further, we introduce the following Lyapunov differential Eq. (21), which allows to guarantee the convergence of the observer:

                  (21)

where s is a positive constant. In fact, the convergence of the proposed observer depends on the gains related with the state estimation and the parameter identification of the system:

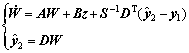              (22)

Let us define the estimation error as

                                 (23)

From Eqs. (20) and (23), the estimation error dynamics are given by

               (24)

As earlier mentioned, consider the following Lyapunov function:

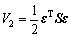                                (25)

There exist real numbers h_min>0 and h_max >0, such that

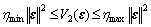                    (26)

Then, taking the time derivative and replacing the suitable terms, it follows that

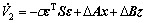                    (27)

The following inequalities hold:

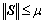,                     (28)

Substituting Eq. (28) into Eq. (27), by regrouping the terms with respect to e, the time derivative of V₂ satisfies the condition:

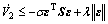                          (29)

where

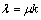                                    (30)

By using Cauchy inequality theory, we have

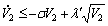                          (31)

where

                                (32)

Next, consider the following change of variable

                                  (33)

The time derivative of u is given by

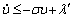                               (34)

and its solution is given by

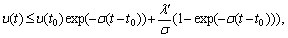
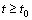                                (35)

Taking the norm of Eq. (32), it is clear that, for t≥t₀, |u(t)| is bounded by a positive constant O₁. Then, for given and positive constants, with r≤O₁, we get

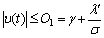                 (36)

Consequently, practical stability is proven. Next, we prove the quasi-stability of the estimation error. It follows that

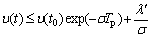for t≥t₀+T_p          (37)

For given O₂, g and T_p positive constants and t₀>0, we have

        (38)

Then, practical strong uniform stability is proven.

4 Experimental verification

To evaluate the effectiveness of the current adaptive observer, some experiments are carried out by the following observer controller scheme shown in Fig. 2.

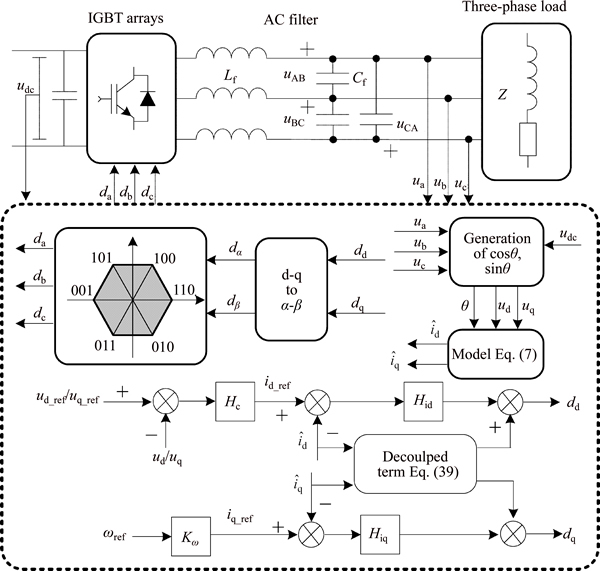
Fig. 2 Controller design block diagram

The implementation method is detailed in Refs. [21, 22]. The purpose of this experimental platform is the industrial implementation test and, therefore, no matter the input or output parameter strictly matches with the actual operating condition.

Due to the reason that the final control object is duty ratio vector d=[d_d d_q], decouple progress is designed as

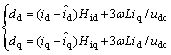                 (39)

where H_u, H_id and H_iq are proportional and integral (PI) controllers and, considering vibration of △w and △u_dc, the compensated are calculated by

             (40)

Note that in Fig. 2 the input desired objects are three-phase voltage and frequency. The desired d_d component can be produced by any u_d or u_q branch. As to d_q, the desired i_{q_ref} is proportional to the given frequency w_ref, and their relationship is

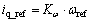                             (41)

where K_w is proportion coefficient which is required to be designed in actual test.

The electric modules of inverter are shown in Fig. 3, and the IGBT arrays (switching voltage of 1200 V, and frequency of 5 kHz) with output AC filter module are contained.

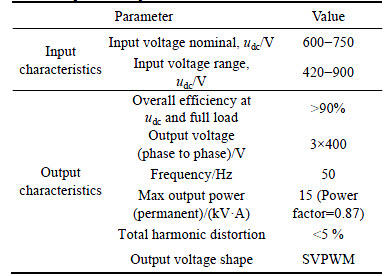
TMS2812F DSP card was used to carry out the real-time algorithm (note that a field-programmable gate array (FPGA) can be also used to implement this observer design). The input and output characteristic parameters of the inverter are listed in Table 1. The AC filter elements with parameters L_f=450 mH and C_f= 820 mF have high voltage endurance ability.

Fig. 3 Electric modules of inverter control circuits

The communication data are captured via the CAN bus, as shown in Fig. 4. A null modem cable with two 9-pin Sub-D connector is used to connect the inverter control unit with the computer. Data are transmitted in serial mode at a rate of 28800 bit/s.

Table 1 Input and output characteristics of tested inverter

The pulse width-modulated signals were generated on the DSP board. The results were recorded using the DSP interfaced with the equipment and personal computer. Three voltage transducers were used to obtain the actual output voltage signal that was solely used for algorithm.

In practice, also it can be seen from Table 1 that, the output frequency deviation is no more than 0.5 Hz. This means that Dw is too small to be ignored, i.e., ||DA||=0. In this case, only deviation of Du_dc was taken into account. In our experimental benchmark, relevant control matrixes were chosen as follows:

,

,

                (42)

Figures 5-8 give the no-load and nominal load experimental results of the adaptive observer for the inverter DC-side voltage jumped from 420 V to 900 V at 0.15 s and after lasting 0.1 s back to 420 V. In order to have a visual comparison, the controlling duty ratio vector d (Value) equals 500'd (Actual).

Figure 5 shows that as the d-axis voltage abruptly changed (no-load, the DC-side voltage deviated about 300 V from stand value of 750 V), the observed output d_α accordingly changed, then the compensated current i_c and voltage u_c in dynamic model Eq. (7) were significantly varied, and within 0.15 s, both of them converged stably. Fortunately, all these adaptations and compensations were carried out by DSP program in a 100 μs calculation period, and finally, the output voltage was held at 400 V and frequency at 50 Hz.

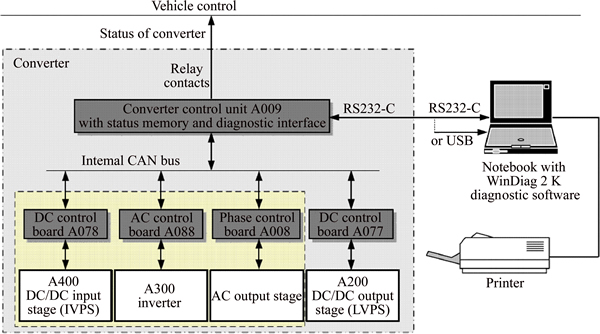
Fig. 4 Data captured via CAN bus and forwarded to computer via interface

Fig. 5 Experimental results with DC-side voltage deviated 300 V from stand value of 750 V (No load)

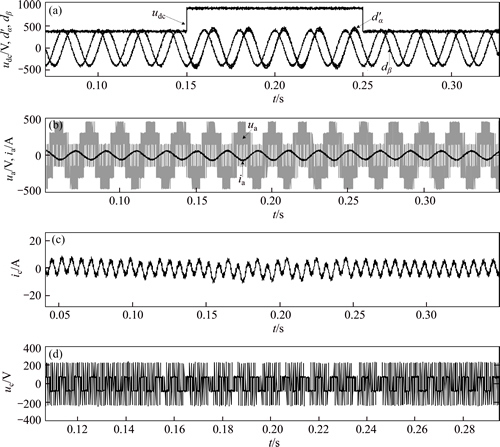
Fig. 6 Experimental results with DC-side voltage deviated 50 V from stand value of 750 V (No load)

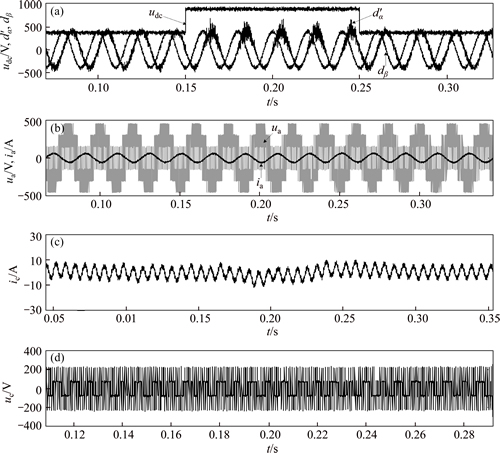
Fig. 7 Experimental results with DC-side voltage deviated 50 V from stand value of 750 V (Nominal load: 15 kV·A)

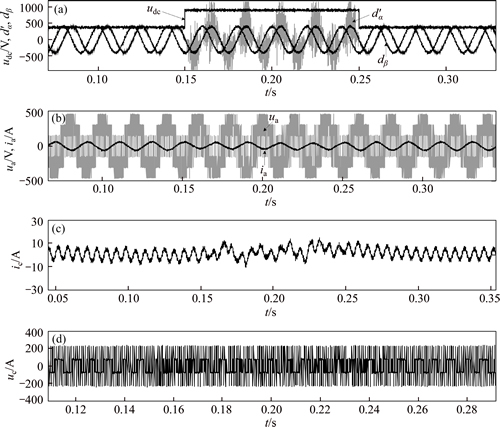
Fig. 8 Experimental results with DC-side voltage deviated 300 V from stand value of 750 V (Nominal load: 15 kV·A)

Figure 6 shows that as the d-axis voltage abruptly changed (no-load, the DC-side voltage deviated about 50 V from stand value of 750 V), the observed output d_α accordingly changed, then the compensated current i_c and voltage u_c in dynamic model Eq. (7) were significantly varied, and within 0.1 s, both of them converged stably. Finally, the output voltage was held at 400 V and frequency at 50 Hz.

Figure 7 shows that as the d-axis voltage abruptly changed (nominal load 15 kV·A, the DC-side voltage deviated about 50 V from stand value of 750 V), the observed output d_α accordingly changed, then the compensated current i_c and voltage u_c in dynamic model Eq. (7) were significantly varied, and within 0.1 s, both of them converged stably. Finally, the output voltage was held at 400 V and frequency at 50 Hz.

Figure 8 shows that as the d-axis voltage abruptly changed (nominal load 15 kV·A, the DC-side voltage deviated about 300 V from stand value of 750 V), the observed output d_α accordingly changed, then the compensated current i_c and voltage u_c in dynamic model Eq. (7) were significantly varied, and within 0.12 s, both of them converged stably. Finally, the output voltage was held at 400 V and frequency at 50 Hz.

5 Conclusions

A nonlinear adaptive stable observer has been designed for the on-board auxiliary inverter in trains. The proposed observer estimates dynamic d-axis and q-axis currents simultaneously. The convergence of the observer has been proven by employing Lyapunov practical stability techniques with consideration of input DC-side voltage parameter vibrations. The effectiveness of the proposed adaptive online identification algorithm has been verified by several experimental results through an industrial product.

References

[1] PRASANNA U R, RATHORE A K. Dual three-pulse modulation- based high-frequency pulsating DC link two-stage three-phase inverter for electric/hybrid/fuel cell vehicles applications [J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(3): 477-486.

[2] OBAYASHI K, TAKAHASHI E, SAKAMOTO A, IYASU S, ANDO S, ONIMARU S. Auxiliary inverter charger (AIC): Concept & experimental results [C]// EVS27 International Battery, Hybrid and Fuel Cell Electric Vehicle Symposium. Barcelona, Spain, 2013: 17-20.

[3] Gao Jun-wei, Yu Jin-peng, Leng Zi-wen. The application of PSO-LSSVM in fault diagnosis of subway auxiliary inverter [J]. ICIC Express Letters, 2013, 4(3): 777-784.

[4] Wu H. Analysis of special characteristic of auxiliary inverter failure based on metro vehicle load fault [J]. Urban Rail Transit, 2012, 15(8): 90-93.

[5] Cheng Liang, Gao Jun-wei, Zhang Bin, Leng Zi-wen, Qin Yong. Fault diagnosis of subway auxiliary inverter based on EEMD and GABP [C]// 26th Chinese Control and Decision Conference (CCDC). Changsha, China: IEEE, 2014: 4715-4719.

[6] Lei Q, Peng F Z, Yang S T. Multiloop control method for high-performance microgrid inverter through load voltage and current decoupling with only output voltage feedback [J]. IEEE Transactions on Power Electronics, 2011, 26(3): 953-960.

[7] TAN Wen, WU Feng, GUO Xiao-ding, ZHOU Lan, YANG Zong- chang, LI Mu, JIANG Feng-ling. Adaptive fuzzy based three-loop composite control of subway auxiliary inverter [C]// 9th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD 2012). Sichuan, China: IEEE, 2012: 531-535.

[8] Holmes D G, Lipo T A, McGrath B P, Kong W Y. Optimized design of stationary frame three phase AC current regulators [J]. IEEE Transactions on Power Electronics, 2009, 24(11): 2417-2426.

[9] ESCOBAR G, VALDEZ A A, LEYVA-RAMOS J, MATTAVELLI P. Repetitive-based controller for a UPS inverter to compensate unbalance and harmonic distortion [J]. IEEE Transactions on Industrial Electronics, 2007, 54(1): 504-510.

[10] Keliang Z, Danwei W, Bin Z, Yigang W. Plug-in dual-mode-structure repetitive controller for CVCF PWM inverters [J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 784-791.

[11] Mohamed Y A, ElSaadany E F. An improved deadbeat current control scheme with a novel adaptive self-tuning load model for a three-phase PWM voltage-source inverter [J]. IEEE Transactions on Industrial Electronics, 2007, 54(2): 747-759.

[12] Hornik T, Zhong Q C. A current-control strategy for voltage- source inverters in microgrids based on H(infinity) and repetitive control [J]. IEEE Transactions Power Electronics, 2011, 26(3): 943-952.

[13] DU Hui-qing, Wang Lei. Study of EMU auxiliary inverter double- loop control strategy with PR controller in nonlinear load condition [C]// 2013 Fourth International Conference on Digital Manufacturing & Automation. Qindao, China, 2013: 1240-1244.

[14] Hasanzadeh A, Onar O C, Mokhtari H, Khaligh A. A proportional-resonant controller-based wireless control strategy with a reduced number of sensors for parallel-operated UPSs [J]. IEEE Transactions on Power Delivery, 2010, 25(1): 468-478.

[15] Mattavelli P, Polo F, Dal L F, Saggini S. Analysis of control-delay reduction for the improvement of UPS voltage-loop bandwidth [J]. IEEE Transactions on Industrial Electronics, 2008, 55(8): 2903-2911.

[16] Turner R, Walton S, Duke R. Robust high-performance inverter control using discrete direct-design pole placement [J]. IEEE Transactions on Industrial Electronics, 2011, 58(1): 348-357.

[17] De D, Ramanarayanan V. Decentralized parallel operation of inverters sharing unbalanced and nonlinear loads [J]. IEEE Transactions on Power Electronics, 2010, 25(12): 3015-3025.

[18] MOHD A, ORTJOHANN E, HAMSIC N, SINSUKTHAVORN W, LINGEMANN M, SCHMELTER A. Control strategy and space vector modulation for three-leg four-wire voltage source inverters under unbalanced load conditions [J]. IET Power Electronics, 2010, 3(3): 323-333.

[19] Tai C P, An C C, Lin L T, Yuan K S. A cooperative imbalance compensation method for distributed-generation interface converters [J]. IEEE Transactions on Industry Applications, 2009, 45(2): 805-815.

[20] Yun W L. Control and resonance damping of voltage-source and current-source converters with LC filters [J]. IEEE Transactions on Industrial Electronics, 2009, 56(5): 1511-1521.

[21] DROBNIK J, BERNOUX B. Power electronics conceptual study for a small urban electric vehicle [C]// EVS25 International Battery, Hybrid and Fuel Cell Electric Vehicle Symposium. Shenzhen, China, 2010: 5-9.

[22] Chen Jie, Wang Lei, Diao Li-jun, Du Hui-qing, Liu Zhi-gang. Distributed auxiliary inverter of urban rail train-load sharing control strategy under complicated operation condition [J]. IEEE Transactions on Power Electronics, 2010, 46(11): 3939-3947.

(Edited by YANG Bing)

Cite this article as: LI Wei, LIU You-mei, CHEN Te-fang, DENG Jiang-ming. An adaptive stable observer for on board auxiliary inverter with online current identification [J]. Journal of Central South University, 2017, 24(3): 819-828. DOI: 10.1007/s11771-017-3484-y.

Foundation item: Project(61273158) supported by the National Natural Science Foundation of China

Received date: 2015-09-07; Accepted date: 2016-05-11

Corresponding author: LI Wei, PhD; Tel: +86-731-82656800; E-mail: liweicsu@csu.edu.cn