J. Cent. South Univ. Technol. (2007)02-0251-04
DOI: 10.1007/s11771-007-0050-z 
Experimental measurement and numerical analysis of fused taper shape for optical fiber coupler
SHUAI Ci-jun(帅词俊), DUAN Ji-an(段吉安), ZHONG Jue(钟 掘)
(School of Mechanical and Electrical Engineering, Central South university, Changsha 410083, China)
Abstract: To find out the effect of the shape of fused taper region on the optical fiber coupler, the fiber couplers were fabricated at different drawing speeds with a six-axes fiber coupler machine. The results, which were obtained from the shape of fused taper region measured with microscope, show that there is a close correlation between the cone angle and optical performance of fiber coupler. High-performance fiber coupler cannot be obtained until rheological shape is controlled accurately. The numerical analysis model, which was built based on generalized Maxwell viscoelastic theory, is resolved with ANSYS software. The calculated results accord with the experimental data. It can apply a theoretic basis for forecasting the shape of fiber coupler fabricated under the conditions of different technological parameters.
Key words: optical fiber coupler; fused biconical taper; viscoelastic model; rheological shape
1 Introduction
With the development of all optical communications, fiber coupler, which is an important passive device, has been widely used in the fields of fiber communication, fiber sensor and so on. At present, it is widely fabricated by the method of fused biconical taper (FBT). FBT coupler has lower cost, lower excess loss, higher directional stability and reliable performance. A lot of researches have indicated that the fiber core can’t carry all the transmission power and the light-wave will be transmitted in new wave-guide that is composed by envelope and air when the core diameter is less than a certain value, and the power will be redistributed in the output port[1-4]. For the light-wave guide, fused taper shape of fiber coupler has a significant influence on its optical performance. In the fabrication process, fibers are heated and fused by flame or other heating device. The fused fibers are drawn to a biconical tape profile by the surface shearing stress. The rheological shape is directly influenced by drawing speed at a certain temperature[5-10]. In this study, the shape of fiber coupler fabricated at different technological parameters was measured and a finite element analysis was presented based on Maxwell viscoelastic theory.
2 Experimental Fused biconical taper setup
Two fibers, whose coating was peeled off and cleaned, were put together and fused on the drawing stage, then they were heated by gaseous flame while the drawing stage moved toward opposite side at a certain speed. The fused region tended to slim during the heating and drawing process and became a biconical taper at last. The fused temperature was obtained by burning C3H6 and O2. The gas flux and drawing speed were controlled with computer. When the light power corresponded to the preset value, the heating and drawing were stopped automatically.
2.2 Coupler preparation and shape testing
Fig.1 shows the typical structure of fused taper fiber coupler. It was made up of two sections: one smooth fused region and one taper region. The total drawing length is marked as Lc; the fused region length is marked as Lb; and the taper region length is marked as L. Lc=Lb+L. d(z) stands for couplers’ sectional diameter, which changes along with axes. The curve of taper region is similar to parabola. Different rheological shapes were accomplished by different fabrication parameters.

Fig.1 Schematic diagram of fused taper coupler
The sectional diameter of different couplers which were fabricated at different parameters, were measured with microscope. Figs.2-5 show different profile curves of coupler fabricated at different drawing speeds. The shape of couplers’ profile is symmetrical. The couplers’ excess loss can be calculated by testing the power at two output ports with light power meter.
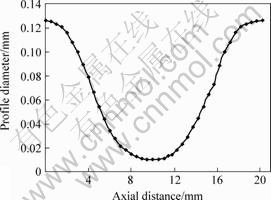
Fig.2 Profile curve of coupler at drawing speed of 0.15 mm/s and excess loss of 0.11 dB
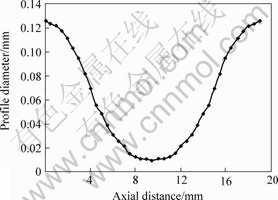
Fig.3 Profile curve of coupler at drawing speed of 0.20 mm/s and excess loss of 0.14 dB

Fig.4 Profile curve of coupler at drawing speed of 0.25 mm/s and excess loss of 0.17 dB
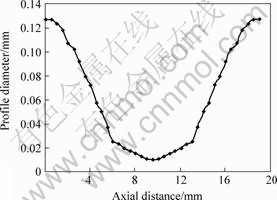
Fig.5 Profile curve of coupler at drawing speed of 0.30 mm/s and excess loss of 0.51 dB
2.3 Experimental results and discussion
Table 1 lists the performance index and technological parameters. It is found that the profile curve in the taper region can be described as two symmetrical exponents according to Figs.2-5. Excess loss is lower when the taper angle is small, and drawing speed has effect on the taper angle.
Table 1 Relationship between taper angle and excess loss

3 Simulation analyses
3.1 Viscoelastic model of fiberglass
Fiberglass is a high-purity silica glass that is a viscoelastic material. Its stress and strain are the function of time and temperature, and its integral constitutive equation under isothermal (T0) condition is [11-12]
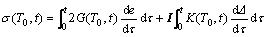 (1)
(1)
where σ is Canchy stress; τ is strain; e is deviatoric part of the strain; Δ is volumetric part of the strain; G(t) is the shear relaxation modulus; K(t) is the bulk relaxation modulus; I is unit tensor and t is relaxation time.
In the glass material the shear deformation mostly occurs at high temperature, so the stress causes the volume strain very small, which can be ignored. The constitutive equation can be described as
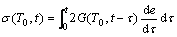 (2)
(2)
where G(t) is a shear relaxation function and also a gradually decreased function. It can be expressed as an expand index form generalized Maxwell mode
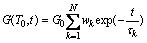 (3)
(3)
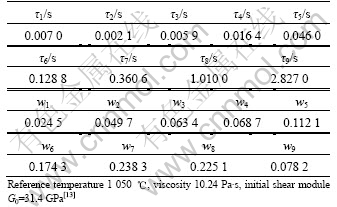
where G0 is initial shear modulus; Nk is the number of Maxwell unit; τk is relaxation time; wk is weight coefficient. Table 2 lists the Maxwell viscoelastic parameters of the fibreglass at 1 050 ℃.
Table 2 Relaxation time and weight coefficient of fiber glass
3.2 Finite element model and boundary condition
Supposed that the flame center is the origin of coordinate, the width of flame region is about 9 mm. Here 10 mm optical fiber is selected to analyze. Because the structure and load of fiber couplers are symmetry on xOy plane, in order to enhance the computing speed, the problem can be simplified to plane problem (as shown in Fig.6).

Fig.6 Model of fused taper
FBT of fiber coupler is a complex dynamic process. Visco88 element, which is a two-dimensional 8-node viscoelastic element in ANSYS software, is chosen to carry out rheological analysis. Fig.7 shows the boundary condition in structural analysis. The boundary condition is: the symmetry plane (y-axis) is loaded with symmetrical restriction, and the x-axis is loaded with axial symmetrical restriction. Temperature, which is 1 200 ℃ measured with thermocouple, is used as body load. And one end of fiber is applied with a fixed drawing speed, which is expressed with a certain displacement in unit time.
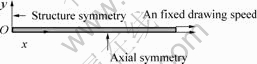
Fig.7 Boundary condition of structural analysis
3.3 Simulation result and analysis
Fig.8 shows the stress field when the fiber coupler is drawn for 2 s at the drawing speed of 0.15 mm/s. It is found that the maximum stress (Maxeqv) is 20.0 MPa at the centre of the fused region when the maximum temperature is 1 200 ℃ and drawing speed is 0.15 mm/s. It is also found that the fibre has stress gradient in radial direction. This is because that the temperature field is asymmetric in radical direction. The central fiber stress is higher than the surface stress inside the flame, and it is lower outside the flame.

Fig.8 Stress field of fiber coupler at drawing speed of 0.15 mm/s
3.4 Rheological shape of fiber coupler
Fig.9 shows the shape curve of fiber coupler when it is drawn at the speed of 0.15 mm/s for 80 s. The final rheological shape of fiber coupler should be a biconical structure. The simulation results are conformed by the experimental testing curve.
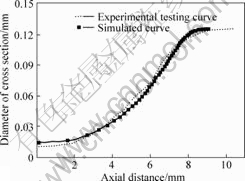
Fig.9 Experimental and simulation shape curves of fused taper region
4 Conclusions
The sectional shape of optical fiber coupler was tested with the microscope. It is found that the sectional shape has close relationship with the excess loss of the optical fiber coupler, that is, the excess loss of the coupler increases while the taper angle increases. Based on the Maxwell viscoelastic theory, the model of FBT was built. Simulation analysis result in the process of FBT is obtained with ANSYS software. The simulation calculations coincide with the experimental measurements.
References
[1] PAL B P, CHAUDHURI P R. Fabrication and modeling of fused biconical tapered fiber couplers[J]. Fiber and Integrated Optics, 2003, 22(2): 97-117.
[2] HSIEH C S, WU T L, CHENG W H. An optimum approach for fabrication of low loss fused fiber couplers[J]. Materials Chemistry and Physics, 2001, 69(1): 199-203.
[3] CHAUDHURI P R, PAL B P. Understanding coupling mechanism in fused fiber coupler-based components: Role of core and cladding modes[J]. The International Society for Optical Engineering, 2001, 4417: 403-411.
[4] KWANG Y S, HWANG I K, YUN S H. High performance fused-type mode selective coupler for two-mode fiber devices[J]. Optical Fiber Communication Conference, 2000, 37(1): 32-36.
[5] EOM J B, KIM J, MOON D S. Single-mode propagation in a photonic crystal fiber coupler[C]// Optical Fiber Communication Conference, Anaheim, CA, USA, 2002, 1(1): 498-507.
[6] YAO S H, HORVATH V K. Measurements of the instantaneous velocity difference and the local velocity with a fiber-optic coupler[J]. Journal of the Optical Society of America A: Optics and Image Science, 2001, 18(3): 696-703.
[7] YANG Yuan-hong, WU Di. Experimental study on fused fiber coupler[J]. The International Society for Optical Engineering, 2001, 4603: 6-9.
[8] SHUAI C J, DUAN J A, ZHONG J. Technical sensitiveness in the rheological manufacture progress of fused taper coupler[J]. Optics and Precision Engineering, 2005, 13(1): 40-44.
[9] NAGATA H. Chemical properties of fused fiber coupler surface[J]. Optical Fiber Technology, 2000, 6(3): 324-328.
[10] DOREMUS R H. Melt viscosities of silicate glasses[J]. Journal of American Ceramic Society, 2003, 82(3): 105-110.
[11] THOMAS F S. Finite-element calculation of stresses in glass parts undergoing viscous relaxation[J]. Journal of American Ceramic Society, 1987, 70 (2): 90-95.
[12] GEORGE W S. Theories of relaxation[J]. Journal of Non-Crystalline Solids, 1990, 123(1/3): 75-89.
[13] SAKAGUCHI S T. Viscosity of silica core optical fiber[J]. Journal of Non-Crystalline Solids, 1999, 244(2): 232-237.
Foundation item: Project (50605063) supported by the National Natural Science Foundation of China; Project(NCET-040753) supported by New Century Excellent Talents in University, China; Project (20050533037) supported by the Doctoral Program of Higher Education, China
Received date: 2006-05-10; Accepted date: 2006-09-12
Corresponding author: DUAN ji-an, Professor; Tel: +86-731-8836858; E-mail:duanjian@mail.csu.edu.cn
(Edited by YANG Bing)