雷达辐射源信号双谱估计的物理意义及其辐射源个体识别
陈涛1，姚文杨1，翟孝霏2，刘雅轩2
(1. 哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨，150001；
2. 中华人民共和国 工业和信息化部 电子科学技术情报研究所，北京，100040)
摘要：针对目前研究中雷达辐射源信号双谱物理意义不明确的问题，给出偏态这一物理概念，并给出雷达辐射源信号偏态的具体表现形式。针对雷达辐射源个体识别，提出应用围线积分双谱估计波形熵和围线积分双谱估计能量熵组成的二维特征向量用于后续的分类识别。在分类识别中，应用分析性能良好的模糊C-均值(FCM)聚类方法，对提取出的二维特征向量加以聚类分析，从而完成在一定信噪比下对雷达辐射源个体的识别。最后，通过仿真实验和实测实验验证本文所述方法的正确性和可行性。
关键词：雷达辐射源个体识别；偏态；双谱估计；围线积分；FCM聚类
中图分类号：TN971.1 文献标志码：A 文章编号：1672-7207(2013)01-0179-09
Bispectrum physical meaning and emitter individual recognition of radar emitter signal
CHEN Tao1, YAO Wenyang1, ZHAI Xiaofei2, LIU Yaxuan2
(1. College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China;
2. Electronic Technology Information Research Institute,
Ministry of Industry and Information Technology of the People’s Republic of China, Beijing 100040, China)
Abstract: Considering the issue that no clear physical significance of radar emitter signal’s bispectrum has been given in the further study, a physical concept of skewness was proposed with its specific performance. For radar emitter individual recognition, two-dimensional feature recognition vector composed of surrounding-line integral bispectrum estimate wave shape entropy and surrounding-line integral bispectrum estimate energy entropy was used to subsequent recognition. In the classification and recognition process, fuzzy C-means (FCM) clustering method which performed well was applied to analyze the clustering two-dimensional feature vector for the further radar emitter individual recognition at the certain signal noise ratio. Finally, computer simulation and actual measured experiment results verified the correctness and effectiveness of this method.
Key words: radar emitter individual recognition; skewness; bispectrum estimation; surrounding-line integral; FCM clustering
随着雷达技术的快速发展，战场信号环境日趋密集复杂，新体制雷达的不断出现使其参数以各种规律变化，应用传统参数进行的识别已经不能满足现代电子战的实际需求；因此，针对雷达辐射源个体识别的研究显得尤为重要。每个辐射源自身都有其相应的特征，各种辐射源特征都分为基本特征和个体特征两大类，本文针对辐射源个体特征进行研究，并对其加以识别。从雷达的原理和相关文献[1-4]可知：雷达辐射源个体特征(又称为雷达无意调制特征、雷达“指纹”特征和雷达“细微”特征)是相对于基本特征而言的，是雷达辐射源自身的固有属性，难以完全去除，并且具有普遍性、稳定性、唯一性和可测性。普遍性说明其特征不是针对某个或某类辐射源而言的。导致唯一性的原因是组成每个辐射源的电子器件之间存在一定的差异，即使是同类型的电子器件，在使用性能上仍然有一定的个体差异[5-6]，且此差异通过长期观测又存在一定的稳定性。而可测性是对其进行个体识别的必要条件。
1 雷达辐射源信号分析
对雷达辐射源个体识别，主要依靠其所发射信号特征的不同这一重要特点加以研究。在理想情况下，发射信号在频域中仅为单根谱线。而在实际情况中，由于噪声和杂散信号对振荡器调幅、调相(或调频)的作用使信号发生一定的畸变，在时域上表现为发射信号相位(或频率)随时间随机变化。
假定理想的发射信号为：
，0≤t≤T (1)
式中：A为信号幅值；fc为信号载波频率；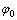
为信号初始相位；T为发射信号的时间。实际的发射信号为：
，0≤t≤T (2)
式中：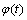
为信号的附带调相噪声即相位噪声；
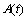为信号附带调幅噪声后的幅度，由于其比相位噪声低10~20 dB[7]，所以，可近似认为
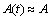。可见：相位噪声是引起辐射源个体差异的首要因素。
为了对实际发射信号进行更准确的描述，可将此信号的相位近似认为受到频率为fm的正弦波信号的调制，即[8]
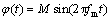(3)
其中：M为调相系数。将式(3)代入式(2)，得：
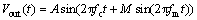(4)
将式(4)展开，可得到：
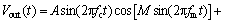
(5)
对式(5)，通常可应用下列关系式进行分解：
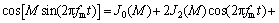
(6)
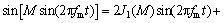
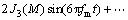(7)
式中：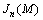
代表调相系数M的0, 1, …, n阶贝塞尔函数[7]。将式(6)和式(7)代入式(5)，考虑贝塞尔函数的近似值为：
，
，
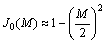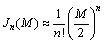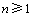(8)
通常在有随机噪声调制的情况下存在如下关系式：
，
，
，
，
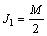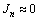(9)
因此，式(4)可近似表示为
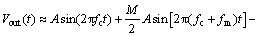
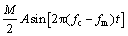(10)
在相位噪声中，fm通常被定义为频率偏移量。由于相位噪声被认为是由无限个随机信号联合调制的结果，fm通常为1个数组，因此，其最终的实际发射信号为：
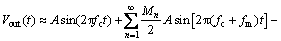
(11)
从式(11)可以看出：实际的发射信号已经不是理想的正弦波信号，其功率谱不再是单根谱线，而是具有一定宽度并伴有边带谱的谱线，如图1所示。其中，纵坐标为功率谱密度归一化结果，各相位噪声的调相系数M和频率偏移量f m均不相同。
2 雷达辐射源信号双谱估计间接法
双谱估计间接法是先估计接收信号的3阶累积量，然后，取其3阶累积量估计的二维傅里叶变换(2D-FFT)的方法。
设接收到的雷达辐射源信号为：
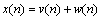(12)
式中：w(n)为高斯白噪声；v(n)即为式(11)中的Vout(t)。w(n)和v(n)是相互独立的。对x(n)求3阶累积量估计，得：
图1 含3类不同相位噪声信号的功率谱与理想信号的功率谱的对比
Fig.1 Comparison between power spectrum contained three kinds of different phase noises’ signals and ideal signal
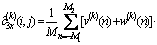
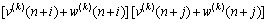(13)
式中：
；
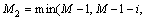
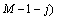；k=1, 2, …, K，为所分的段数；i和j为延迟点数。将此表达式展开合并后，得到：
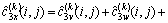
(14)
当信号和高斯白噪声的均值都为0时，式(14)可变为
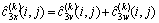(15)
对K段的3阶累积量估计加和取平均值作为整个被分析信号的3阶累积量估计，即
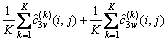(16)
由于其双谱估计为其3阶累积量估计的2D-FFT，所以，此接收信号的双谱估计为
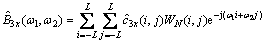(17)
式中：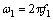
；
；
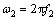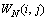为所加入的二维窗函数。
从式(14)可知：只有无限次采样且w(n)是高斯白噪声时，才有
，
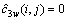。但现实中的信号均是有限长的，所以，
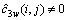，接收信号的
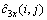也必然受高斯白噪声的影响。由于2D-FFT不改变信号的相关特征，所以，其双谱估计
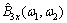也近似服从高斯白噪声的相关特征[9]。
3 雷达辐射源信号双谱的物理意义
高阶谱的物理意义不明确是其功率谱应用不广泛的主要原因。归一化的二阶零滞后累积量定义为信号的方差，而功率谱正是信号方差在频域上的分解，是表征信号能量随频率变化的分布函数[10]。双谱没有功率谱这样清晰的物理意义，在本文中可理解为信号的偏态在双谱域上的分解。归一化的3阶零滞后累积量表现为非对称分布的偏斜状态，可认为是信号的偏态。
这里所分析的相位噪声与图1中所加入的相位噪声完全相同。高斯白噪声的偏态分布函数与3类不同相位噪声的偏态分布函数的对比见图2，其中偏态分布区间采用了基于峰值的归一化处理。从图2可看出：高斯白噪声的偏态分布函数与正态分布函数相一致，而相位噪声本质上不同于高斯白噪声。偏态分布函数如图2所示。从偏态分布函数的定义可知：图1中的相位噪声分布函数均为正偏态分布函数。
图2从偏态分布函数的角度证明了相位噪声与高斯白噪声有着本质上的区别，同时，也验证了雷达辐射源个体之间的相位噪声的确存在一定的差异，可作为识别其所对应个体的重要依据。
信噪比RSN=15 dB时理想信号的偏态分布函数与3类辐射源信号的偏态分布函数的对比结果见图3。从图3可知：高斯白噪声使辐射源信号的偏态分布函数近似服从高斯白噪声的正态分布函数，而相位噪声差异所引起的偏态分布函数之间的差异不能体现出辐射源个体之间的差异：所以，如何在最大限度地突出辐射源个体之间差异的同时，将高斯白噪声的影响降至最低，正是辐射源个体识别的关键所在。
图2 高斯白噪声的偏态分布函数与3类不同相位噪声的偏态分布函数的对比
Fig.2 Comparison between skewness distribution function of gauss noise and three kinds of different phase noises
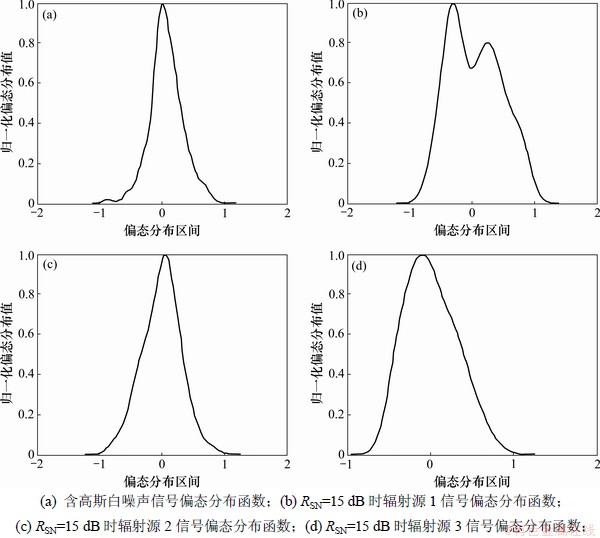
图3 RSN=15 dB时理想信号的偏态分布函数与3类辐射源信号的偏态分布函数的对比
Fig.3 Comparison of skewness distribution function between ideal signal and three kinds of emitter signals at RSN=15 dB
4 围线积分双谱估计及其二维特征提取
在信噪比RSN=15 dB时，对接收到的3类辐射源信号，应用前面所述方法对其进行计算，其接收信号总的时间采样点数均为1 024点，分成16段，每段64点，2D-FFT点数为64点，对计算结果均进行归一化处理后，所得结果见图4。
从图4可以看出：高斯白噪声对3类辐射源信号双谱估计有一定影响，同时，3类辐射源信号的归一化双谱估计有明显的差异。
围线积分双谱估计比普通双谱估计对高斯白噪声具有更强的抑制能力，因为双谱估计是由单个双谱估计值组成的二维矩阵，若双谱估计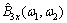的方差为
，则双谱估计中的每个双谱估计值的方差也为；而围线积分双谱估计的1个特征值是由N个双谱估计值
共同累加求和得到的，所以，围线积分双谱估计的方差也为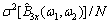
[9]，这在一定程度上抑制了高斯白噪声的影响。
围线积分的路径如图5所示。从图5可见：围线积分双谱估计的积分路径是以原点为中心的正方形，每个黑点代表1个双谱估计值。与其他积分双谱估计相比，其优点是不会导致某些双谱估计值被遗漏，也不会导致某些值被多次利用。
对图4(a2)，(b2)和(c2)所示等高图，应用图5所示的围线积分路径进行计算，可得到3类辐射源信号在RSN=15 dB时的围线积分双谱估计波形，如图6所示。
为降低计算的复杂度，并使辐射源个体识别更加直观，本文引入围线积分双谱估计波形熵和围线积分双谱估计能量熵作为二维特征向量，以衡量辐射源个体之间的差异。
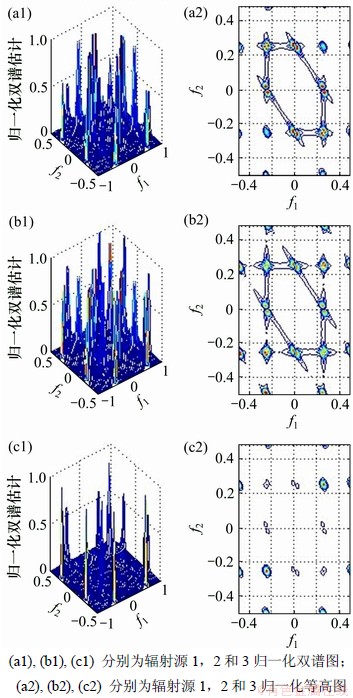
图4 RSN=15 dB时3类辐射源信号的归一化双谱估计三维图和等高图
Fig.4 Normalization bispectrum estimation 3D map and contour map of three kinds of emitter signals at RSN=15 dB
图5 围线积分的路径
Fig.5 Integral track of surrounding-line
图6 3类辐射源信号在RSN=15 dB时的围线积分双谱估计波形
Fig.6 Surrounding-line integral bispectrum estimation wave value of three kinds of emitter signals at RSN=15 dB
围线积分双谱估计波形熵是用于衡量其波形能量沿其积分路径的发散程度的，其定义为[11]：
(18)
设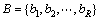
，R为积分圈数，
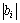(i=1, 2, …, R)为每一圈上的双谱估计值的总和，
为全部圈上的双谱估计值的总和，则
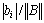为每一圈积分路径上的双谱估计值总和占其全部圈上双谱估计值总和的概率。
围线积分双谱估计能量熵用于衡量其在二维平面内能量的分布，设归一化后的双谱估计矩阵为
，则：
，
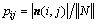(19)
式中：
为此双谱估计值的总和；pij为1个双谱估计值占其双谱估计值总和的概率。则围线积分双谱估计能量熵为[12]：
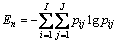(20)
由Eb和En联合组成的二维特征识别向量[Eb, En]反映了本文所述的雷达辐射源个体特征。综上所述，雷达辐射源个体识别的步骤如下。
(1) 收集截获的由不同雷达辐射源个体所发射的信号，并对信号进行零均值化处理。
(2) 对零均值化后的信号应用前面所述方法进行计算，并对其结果进行归一化处理。再根据图5所示的积分路径对其处理后的结果进行围线积分计算。
(3) 根据式(18)计算围线积分双谱估计波形熵，根据式(20)计算围线积分双谱估计能量熵，将其两者组成[Eb, En]，作为辐射源个体识别的特征，并可依此建立雷达辐射源个体识别的特征数据库，作为后续雷达辐射源个体识别的相应重要依据。
5 实验与分析
5.1 仿真实验与分析
实验信号为单载频正弦波信号，且每类辐射源个体均发射60个，其功率谱如图1所示。信号载波频率fc=500 MHz，接收机采样频率fs=2 GHz，信号总时间采样点数为1 024点，被分为16段，每段64点，2D-FFT点数为64点，信噪比RSN=15~25 dB。应用本文所述方法对其进行特征提取。为了去掉信号功率变化对信号双谱估计的影响，对信号的双谱估计结果均进行归一化处理。应用FCM聚类法对提取出的[Eb, En]进行识别，FCM聚类法最大迭代次数为200次，预订的类别数目c=3，即有3个聚类中心[13-14]。
图7(a)所示为FCM聚类前3类辐射源个体特征的分布情况。从图7(a)可以看出：应用本文所述方法提取的3类辐射源个体特征之间具有一定的自然聚类性，但由于辐射源1和辐射源2之间的个体特征差异较小，对高斯白噪声敏感，使得其在RSN=15 dB时出现了混叠现象，这对后续辐射源个体识别的结果也必将产生影响(以下各图中：*表示辐射源1的个体特征；○表示辐射源2的个体特征；△表示辐射源3的个体特征；直线代表FCM聚类后，此个体特征隶属于那个辐射源个体)。
图7(b)所示为经过FCM聚类后得到的结果。从图7(b)可以看出：原先自然分布的个体特征被聚类成3类，并且每一类个体特征都围绕在其最终的聚类中心周围。由于辐射源1和辐射源2的个体特征之间出现了混叠现象，导致出现图7(b)中的错误隶属关系，产生了错误的聚类结果，从而影响了辐射源的个体识别。
图8(a)所示为RSN=20 dB时FCM聚类前3类辐射源个体特征的自然分布情况。将图8(a)与图7(a)相比可以看出：在提高RSN的同时，其个体特征之间的混叠现象也有所减弱，因此，应用本文所述方法提取的3类辐射源个体特征之间的自然聚类效果也较明显。
图8(b)所示为经过FCM聚类后的结果。从图8(b)可以看出：3类辐射源个体特征被聚类为3类，并且聚类结果良好。除辐射源3的1个个体特征发生错误识别外，其余各特征的聚类结果均正确，与图7(b)相比，聚类错误大大降低。
RSN=15~25 dB时3类辐射源个体的正确识别概率如图9所示。从图9可以看出：应用本文所述方法在较低RSN下的正确识别概率均大于80%，其中由于辐射源3个体特征与其他2类辐射源个体特征的差异较大，所以，辐射源3个体特征识别为其自身的正确识别概率均在95%以上；随着RSN的不断提高，其正确识别概率也不断上升，当RSN＞21 dB时，正确识别概率均稳定于100%。
图7 3类辐射源个体特征在RSN=15 dB时FCM聚类前、后的分布对比
Fig.7 Individual feature distribution of three kinds of emitters before and after FCM clustering at RSN=15 dB
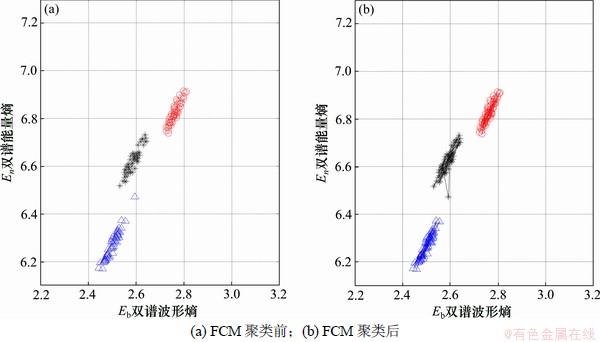
图8 3类辐射源个体特征在RSN=20 dB时FCM聚类前、后的分布对比
Fig.8 Individual feature distribution of three kinds of emitters before and after FCM clustering at RSN=20 dB
图9 RSN=15~25 dB时3类辐射源个体的正确识别概率
Fig.9 Individual correctly recognizing probability of three kinds of emitters at RSN=15-25 dB
5.2 实测实验与分析
为了进一步验证本文所述方法的有效性与真实性，本文给出在实验室环境中，实测的3类辐射源信号的分析结果，如图10所示。
信号接收端应用自主研制的16通道10 bit数字接收机，其中A/D器件为美国国家半导体公司生产的ADC10D1000，采样频率设定为fs=1.92 GHz，信号发射端均为fc=500 MHz的3类不同辐射源所发射的共180个连续正弦波信号，且每个辐射源均发射60个，其每个接收信号的时间采样点数均为1 024点，即时间长度为0.533 μs，信号发射功率均为1 dBm，RSN=41.356 1 dB。从图10可直观看出：应用本文所述方法提取的3类实测辐射源个体特征之间的差异明显，自身个体特征的自然聚类性良好。为进一步验证本文所述方法的正确性，应用FCM聚类法对其结果进行聚类分析验证，其验证结果可用于接收端正确识别此接收信号来自于实际辐射源个体，进而从实测角度证明了应用本文所述方法的真实性与有效性。
图10 3类实测辐射源个体特征FCM聚类后的分布
Fig.10 Individual feature distribution of three kinds of actual measured emitters after FCM clustering
6 结论
(1) 对雷达辐射源信号双谱物理意义进行解释，从新的角度说明了相位噪声与高斯白噪声之间的本质区别，也直观地体现了实际情况中高斯白噪声对辐射源个体识别的影响。采用双谱估计降低了高斯白噪声对辐射源个体识别的影响。
(2) 降低了高斯白噪声对辐射源个体识别的影响。提出了基于围线积分双谱估计间接法的分析方法；应用波形熵和能量熵将分析结果组成二维特征向量[Eb, En]；应用性能良好的FCM聚类方法对[Eb, En]进行聚类分析。
(3) 通过仿真试验和实验室实测数据实验，验证了算法的有效性，表明文中提出的应用围线积分双谱估计波形熵和围线积分双谱估计能量熵组成的二维特征向量，可以作为雷达的指纹特征用于雷达辐射源个体识别。
参考文献：
[1] 田波, 龙良将, 段洪. 雷达辐射源信号无意调制的加入方法分析及仿真[J]. 电子测量技术, 2010, 33(5): 42-45.
TIAN Bo, LONG Liangjiang, DUAN Hong. Implementation analysis and simulation of radar emitter signals’ unintentional modulation[J]. Electronic Measurement Technology, 2010, 33(5): 42-45.
[2] 陈刚. 锁相环路的相位噪声分析[J]. 科技信息, 2009(3): 112-113.
CHEN Gang. Phase noise analysis of phase-locked loop[J]. Science & Technology Information, 2009(3): 112-113.
[3] 许丹, 姜文利, 周一宇. 雷达功放正弦激励下的无意调制特征分析[J]. 系统工程与电子技术, 2008, 30(3): 400-401.
XU Dan, JIANG Wenli, ZHOU Yiyu. Unintentional modulation feature analysis of radar’s power amplifier with simple ton driven signal[J]. Journal of Systems Engineering and Electronics, 2008, 30(3): 400-401.
[4] Kim Y W, Yu J D. Phase noise model of single loop frequency synthesizer[J]. IEEE Transactions on Broadcasting, 2008, 54(1): 112-119.
[5] 余志斌. 基于脉内特征的雷达辐射源信号识别研究[D]. 成都: 西南交通大学信息科学与技术学院, 2010: 6-7.
YU zhipin. Study on radar emitter signal identification based on intra-pulse features[D]. Chengdu: Southwest Jiaotong University. School of Information Science & Technology, 2010: 6-7.
[6] Molchanov P O, Astola J T, Egiazarian K O, et al. Target classification by using pattern features extracted from bispectrum-based radar Doppler signatures[C]//International Radar Symposium, IRS 2011. Leipzig, Germany, 2011: 791-796.
[7] Robins W P. 相位噪声[M]. 秦士, 姜尊富, 译. 北京: 人民邮电出版社, 1988: 10-11, 43-44.
Robins W P. Phase noise[M]. QIN Shi, JIANG Zunfu, trans. Beijing: Posts & Telecom Press, 1988: 10-11, 43-44.
[8] 陈韬伟. 基于脉内特征的雷达辐射源信号分选技术研究[D]. 成都: 西南交通大学计算与通信工程学院, 2010: 58-61.
CHEN Taowei. Deinterleaving technology for radar emitter signals based on the intra-pulse features[D]. Chengdu: Southwest Jiaotong University. School of Information Science & Technology, 2010: 58-61.
[9] 马君国, 肖怀铁, 李保国, 等. 基于局部围线积分双谱的空间目标识别算法[J]. 系统工程与电子技术, 2005, 27(8): 1490-1493.
MA Junguo, XIAO Huaitie, LI Baoguo, et al. Space target recognition algorithm based on local surrounding-line integral bispectrum[J]. Journal of Systems Technology and Electronics, 2005, 27(8): 1490-1493.
[10] YU Haitao, WANG Yingmin, XIE Zhanlin, et al. Feature extraction and classification based on bispectrum for underwater targets[C]//2010 International Conference on Intelligent System Design and Engineering Application, ISDEA 2010. Changsha, 2010: 742-745.
[11] 郝明, 郭汝江. 基于波形熵的异步窄脉冲干扰抑制[J]. 信息化研究, 2009, 35(5): 42-44.
HAO Ming, GUO Rujiang. Method of nonsynchronous short- pulse jamming suppression based on waveform entropy[J]. Informatizaton Research, 2009, 35(5): 42-44.
[12] 关键, 张建. 基于固有模态能量熵的微弱目标检测算法[J]. 电子与信息学报, 2011, 33(10): 2494-2499.
GUAN Jian, ZHANG Jian. Weak target detection based on intrinsic mode energy entropy[J]. Journal of Electronics & Information Technology, 2011, 33(10): 2494-2499.
[13] 赵欢, 王培红, 钱瑾, 等. 基于模糊C-均值聚类的锅炉监控参数基准值建模[J]. 中国电机工程学报, 2011, 31(32): 16-21.
ZHAO Huan, WANG Peihong, QIAN Jin, et al. Modeling for target-value of boiler monitoring parameters based on fuzzy C-means clustering algorithm[J]. Proceedings of the CSEE, 2011, 31(32): 16-21.
[14] 高新波. 模糊聚类分析及其应用[M]. 西安: 西安电子科技大学出版社, 2004: 53-59.
GAO Xinbo. Fuzzy clustering analysis and its application[M]. Xi’an: Xi’an University of Electronic Science and Technology Press, 2004: 53-59.
(编辑 陈灿华)
收稿日期：2011-12-28；修回日期：2012-02-22
基金项目：国家自然科学基金资助项目(61201410/F01301)；中央高校基本科研业务费专项资金资助项目(HEUCF120802)
通信作者：陈涛(1974-)，男，辽宁铁岭人，博士，副教授，从事宽带信号检测、处理及识别的研究；电话：0451-82519804；E-mail: chentao@hrbeu.edu.cn
