Trans. Nonferrous Met. Soc. China 23(2013) 3153-3160

Strategic equilibrium price analysis and numerical simulation of preponderant high-tech metal mineral resources

Mei-rui ZHONG^1,2, Jie-yu CHEN¹, Xue-hong ZHU^1,2, Jian-bai HUANG^1,2

1. School of Business, Central South University, Changsha 410083, China;

2. Institute of Metal Resources Strategy, Central South University, Changsha 410083, China

Received 25 August 2013; accepted 15 September 2013

Abstract: Based on exploitation compensation value system of preponderant high-tech metal mineral resources and distortion of pricing mechanism, social utility function was constructed to modify decision utility function of developers, and was extended to Stackelberg production decision model of preponderant high-tech metal mineral resources development. Analyzing the influences on market monopoly, output and price decision-making exerted by altruistic preferences, inequity aversion and sequential reciprocity fairness belief equilibrium, game fairness equilibrium which is significant in experimental economics can be obtained and verified by numerical simulation. In process of strategic pricing, method that uses the variation of producer surplus to measure strategic value from psychological preferences was proposed for the first time and technical support to improve exploitation compensation value system of preponderant metal mineral resources was available.

Key words: metal; high-tech mineral; mineral resources; equilibrium price; numerical simulation

1 Introduction

According to the results of the Strategic Research on High-tech Mineral Exploration and Exploitation, metal mineral resources such as rare earth, antimony, lithium and indium, which belong to preponderant high-tech metal mineral resources in China, are vital and irreplaceable in economic, technological and military development relating to a country’s national defense and economic security. There are two kinds of factors accounting for market power weakening in China as a monopoly supplier in preponderant high-tech metal mineral resources. One kind is internal cause, such as, overdevelopment of preponderant strategic high-tech metal mineral resources, market order disorder, low degree of industrial concentration, low technology level and absence of reserve system. The other is leverage factor, namely, import states as USA and Japan integrate their domestic scattered purchasing power to import in a monopolistic way and carry out strategic metal reserve policies. All these result in weak bargaining ability and lack of pricing power in the practical long-term contract pricing of preponderant high-tech metal mineral resources. However, under current industrial and resource taxes policies in China, the underlying reason may be that the developers ignore strategic value generated from changes in monopoly market structure caused by psychological preferences in the process of mining [1,2]. Based on the analysis of social preferences equilibrium, a fair and reasonable exploitation and utilization compensation price of preponderant high-tech metal mineral resources must achieve equilibrium among all sorts of game parties as a result of a fairness game [3,4], otherwise, it is hard to achieve success. The traditional equilibrium game evaluation method could reflect the economic value of preponderant high-tech metal mineral resources exploitation and utilization accurately; however, the unfairness caused by some players is difficult to accept. Therefore, the exploitation and utilization of preponderant high-tech metal mineral resources being commonly accepted by each subject is in need of not only reflecting the identity of the economic value and ecological value of exploitation and utilization accurately, but also earning the recognition of fairness of development compensation prices by each party. As has been mentioned above, social preferences equilibrium evaluation is used to modify the framework of development compensation value system of metal mineral resources, and social preferences are added into the Stackelberg production decision model in specific to analyze the mechanism of strategic equilibrium price caused by social preferences, and it is of necessity to improve the exploitation compensation value system and the mineral resources pricing mechanism.

Large sums of studies concerning with metal mineral resources oligopoly price agreement are as follows. TRUBY [5] established an incomplete market structure model to study how the inter-temporal variation caused by a variety of market forces (such as the depletion allowance, monopoly, externalities, price controls and international shocks) affects inter-temporal metal resources configuration; SANTOS-PINTO [6], and KOIDEA and SANDOHB [7] analyzed exhaustible metal resource exploitation monopoly market structure model based on two different demand elasticity markets; CARDELLA and CHIU [8] analyzed parallel redundant system based on n dimensions and illustrated the circumstances in which metal mineral resource developers can gain more profit on the basis of Stackelberg game model; BREITMOSER [9] compared several equilibrium models such as Cournot model, Stackelberg model, Bertrand model of Nash equilibrium and different equilibria formed by monopoly price competition. The study of social preferences concentrated on the development of decision-making utility function, including fairness equilibrium model by RABIN, modified sequential interactive equilibrium model by DUFWENBERG and KIRCHSTEIGER, modified reciprocal fairness equilibrium model by FALK and FISCHBACHER, inequity aversion model based on distribution outcomes by FEHR and SCHMIDT, and BOLTON and OCKENFELS, and mixture models combined with interaction, intention and social preferences effectively [10-14]. Some scholars took fairness into the wholesale chain pricing process according to those models aforementioned [15,16]. Deduced from the above researches, in pricing process of the metal mineral resources agreement with oligopolistic nature, as long as a preference associated belief is given to related subject, exploitation values of metal mineral resources will depend on not only the benefits it brought, but also psychological effects contained by preference belief. Then, interrelated pondering on preferences belief analysis and metal mineral resources development evaluation is established. On account of this interrelated pondering, social preferences are integrated into the preponderant high-tech metal mineral resources development compensation pricing process, building up associated valuation between social preferences and strategic price.

2 Utility function modification

In a complete competitive market, the equilibrium price of preponderant high-tech metal mineral resources development and utilization can make fair distribution, achieve optimal status and maximize social welfare, which would maximize the interests of all parties as a fair price. However, the market structure of preponderant high-tech metal mineral resources development and utilization is generally oligopolistic, which will make the price higher than the perfect competitive market equilibrium prices and twist Pareto optimal allocation. In the oligopolistic market structure, the preponderant high-tech metal mineral resources development and utilization are eventually commonly accepted by each subject, not only reflecting the recognition of economic value accurately, but also meeting the recognition on fair prices of development compensation psychologically. However, in oligopolistic market structure, the preponderant high-tech metal mineral resources development is rather slow initially, and for the sake of short-term interests, the developers will reach exhaustion horizontal line at speedy rate under distortionary cost system. Therefore, the supply is in sub-optimal status in the oligopolistic market structure; the shadow price of preponderant metal mineral resources will be deviated from the fair equilibrium price.

Thus, in incomplete competitive market structure, fair price reflects not only the fair compensation of intrinsic value of preponderant high-tech metal mineral resources products, but also the equilibrium fluctuations in supply and demand of the intrinsic value compensation. From the viewpoint of behavioral economics, the impact of stakeholders’ fairness belief on the shadow price and profit should be considered into fair trade power. However, the strategic value and the fairness can be measured by social utility function. In the oligopolistic market structure, the revision of psychological preferences on the preponderant high-tech metal mineral resources developers’ decision-making utility function is as follows. If developers have interdependent preferences, their utility function should incorporate the psychological effects of social preferences as follows:

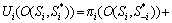
               (1)

where S_i is the output strategy of oligopolist i, 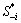 is the output strategy of remaining oligopolists, π_i is oligopolist i profits without considering interdependent preferences, π_j is the profit of other oligopolists without considering interdependence preferences, and w_ij is the coefficient of strategic interaction measuring the profit that oligopolist i gives to other oligopolists. Positive values of the coefficient w_ij mean that player i is willing to sacrifice his payoff from outcomes in order to increase the payoff of player j. Negative values mean that player i is willing to sacrifice his payoff from outcomes in order to lower player j payoff. In addition, 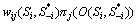can be decided by different types of social preferences as follows:

1) If the oligopolist prefers intergenerational fairness, that is, the oligopolist considers the intertemporal allocation of preponderant high-tech metal mineral resources development and the utilization of later generations, then the oligopolists have slight altruistic preferences, and w_ij is positive.

2) For types of inequity averse player, 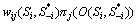can be replaced by 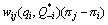. 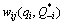is used to measure the deviation profit function of oligopolist i putting weights on oligopolist j as follows:

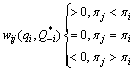
The first condition expresses aversion to advantageous inequity, namely if oligopolist i’s profits are greater than those of oligopolist j, then oligopolist i is willing to sacrifice own profits to increase j’s profits. The third condition expresses aversion to disadvantageous inequity. If oligopolist i’s profits are lower than those of oligopolist j, then oligopolist i is willing to sacrifice own profits to reduce j’s profits.

3) If it is the interactive fairness preference, the payoff function of the oligopolist i is

     (2)

where is oligopolist i’s profits and 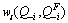 is the weight that oligarch i places on its rivals gross profits, i.e. 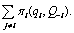As usual, oligopolist i’s profits depend on its output q_i, and on the gross output of its rivals, Q_-i, the equation is

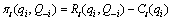
where 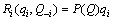 is revenue. Assuming that the weight on its rivals gross profits placed by oligopolist i depends on own gross output  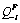and that of his rivals. Furthermore, it can be assumed that:

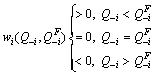
That is, when 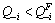, the oligopolist i has a positive weight on rivals’ gross profits; when 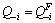, the weight is 0; it has a negative weight on its rivals’ output when 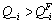. These conditions reveal the real intention of oligopolist with reciprocal fairness preference to care rivals. The DK fairness equilibrium determination method used by reciprocal fairness psychological compensation value modification is that game subjects are willing to sacrifice their material interests to help people who treat them kindly and to punish people who treat them badly; the smaller the sacrifice is, the greater the motivation that they get to help and punish.

3 Strategic equilibrium price changing

Based on the revised developers’ utility function, the developers will play strategic interaction game on production when exploiting preponderant high-tech metal mineral resources, meanwhile they can tell that the industry is oligopoly by judging from the market concentration indicators of CR₂, CR₄ of lithium, antimony, indium and rare earth. Therefore, developers of preponderant high-tech metal mineral resources will play oligopolistic interactive fair game. In accordance with the actual pricing situation of lithium, antimony, indium and rare earth, decision-making of production exhibits Stackelberg nature, that is, market leader sets the production first in oligopolistic preponderant high-tech metal mineral resources market, subsequently, some followers decide their own production, namely decision-making of production is sequential. Therefore, the Stackelberg game model is fit to analyze the impacts of fairness equilibrium factors on strategic price of preponderant high-tech metal mineral resources development. In order to achieve the goal better, it is assumed that fixed costs are not considered, nor the impact of product efficiency on marginal costs, i.e., developing and utilizing these metals share the same marginal cost of production, namely, c, the leaders’ production of preponderant high-tech metal mineral resources is q₁, while the followers’ is q₂, the entire production of the oligopolistic markets is 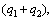 linear inverse demand function of mineral resources products in oligopolistic market is p=a-q₁-q₂. Based on the solution of equilibrium in Stackelberg model, perfect Nash equilibrium at sub-game of Stackelberg game model under the hypothesis of self-serving oligarchs is arrived:

((a-c)/2, (a-c)/4)                             (3)

3.1 Strategic equilibrium price changing under altruistic preferences

Introducing preponderant high-tech metal mineral resources developers’ altruistic behavior as well as the followers’ non-altruistic behavior into the traditional Stackelberg game model whose degree is, respectively, then the profit function of oligarchic preponderant high-tech metal mineral resources developers can be written as follows:

h₁(q₁, q₂)=q₁(a-q₁-q₂-c)+εq₂(a-q₁-q₂-c)          (4)

h₂(q₁, q₂)=q₂(a-q₁-q₂-c)                      (5)

Based on the solution of Stackelberg game model, partial derivative equation of equation is 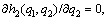 then the development followers’ best response function of preponderant high-tech metal mineral resources is

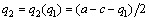                     (6)

When Eq. (6) is inserted into Eq. (4), the partial derivative equation can be expressed as h₁(q₁, q₂(q₁))/ q₁=0, then reaching the altruistic Stackelberg Nash equilibrium:

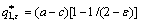                      (7)

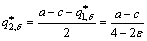                     (8)

From Eqs. (7) and (8), it can be obtained that when altruism level of the leaders in this market increases, their production 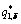 decreases, while followers’ strategic production  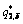increases. This shows that the leaders in preponderant high-tech metal mineral resources development are more selfless by reducing their own production for the followers’ benefit. According to the market equilibrium, the production can be obtained as follows:

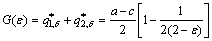           (9)

From Eq. (9), it can be concluded that when altruism degree ε of the leaders in preponderant high-tech metal mineral resources development increases, the market’s total output G(ε) decreases. This shows that the higher the altruism degree of the leaders in this market present is, the more monopolistic the market is. Similarly, the opposite is also true. The products’ price of leaders in preponderant high-tech metal mineral resources development is p=a-G(ε), where the altruistic level of the leaders increases, and the market price increases. Assuming x=1/(2-ε)∈[1/2, 1] in following sections then x can be seen as a monotonically increasing function of ε.

3.2 Strategic equilibrium price changing under inequity aversion

In the development compensation pricing of preponderant high-tech metal mineral resources, oligopolists show sympathy preference and jealousy preference on the players’ payoffs, that is to say, they will sacrifice their profits to lower those oligarchs who obtain higher profits, but also sacrifice their profits to upgrade those oligarchs who bear lower profits. According to FEHR and SCHMIDT’s definition of inequity aversion, the payoff functions of preponderant high-tech metal mineral resources development and utilization are affected by oligopolists’ inequity aversion preferences, thus their payoff functions are

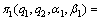
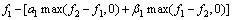   (10)

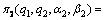
   (11)

where α_i (i=1, 2) is inequity aversion jealousy preference coefficient of oligopolist i, β_i (i=1, 2) is the inequity aversion sympathy preference coefficient, moreover, α_i>β_i>0. According to the traditional Stackelberg equilibrium analysis, leaders have first-mover advantage in sequential decision making, so the leaders in the sequential decision-making should show sympathy preference, while the followers should show jealousy preferences. Thus, the leaders’ and followers’ utility function of preponderant high-tech metal mineral resources in Stackelberg game can be respectively written as

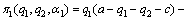
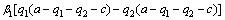     (12)

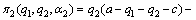
   (13)

where β₁ is the inequity aversion sympathy preference coefficient of the leaders, and α₂ stands for inequity aversion jealousy preference coefficient of the followers. According to the optimal Stackelberg equilibrium analysis, the best response function of the followers derived from payoff functions under the condition of inequity aversion is as follows:

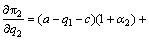
                   (14)

From Eq. (14), the optimal production of the followers is

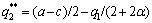                   (15)

When Eq. (15) is inserted into Eq. (13), the optimal production of the leaders is presented as

      (16)

Furthermore, using Eq. (16) in Eq. (12), the optimal production of the followers can be finally written as

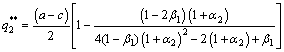    (17)

The function of production under fairness equilibrium exhibits that under piecewise linear inequity aversion condition, the best-response function of oligarch and standard Stackelberg equilibrium game are both continuous, but the former is no longer monotonous. The difference between the inequity aversion and self-serving Stackelberg equilibrium is

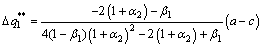
Since (a-c)/|4(1-β₁)(1+α₂)²-(1+α₂)+β₁| is positive, the leaders’ production under fairness preference condition decreases compared with that under self-serving condition. Similarly, comparing the followers’ Stackelberg equilibrium production under these two conditions, and α₁, β₁ fall in the interval (0.15, 0.50), the output of fairness preference follower is less than that of self-serving follower.

Such results show the effects of sympathy and jealousy on the Stackelberg equilibrium. Since lithium, antimony, indium and rare earth are raw industrial materials and difficult to be replaced, the price elasticity of demand is relatively low. When considering inequity aversion, the market capacity is reduced, resulting in higher prices. According to the relationship between demand price elasticity and revenue, the preponderant high-tech metal mineral resources developers own greater producer surplus, which is the value of strategic interaction generated from inequity equilibrium, so that the value of strategic interactions should also be included in the value of the compensation systems.

3.3 Strategic equilibrium price changing under sequential reciprocity fairness

According to the definition of DK sequential interaction fairness equilibrium, leaders’ and followers’ payoff function of preponderant high-tech metal mineral resources development are

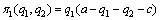                   (18)

                  (19)

In sequential decision-making of preponderant high-tech metal mineral resources, the leaders can maximum benefit when the followers’ output is zero, while minimize their possible benefit when their own output is zero and under which the profit is zero; the followers’ situation is much the same. So we have the following conclusions:

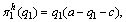
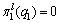              (20)

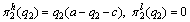              (21)

According to the definition of sequential reciprocal fairness equilibrium, the preponderant high-tech metal mineral resources followers’ goodwill of strategic choices of production level 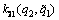 is  the difference between the benefits which are brought by followers’ decision for the followers and the average benefit that the followers can bring to the leaders. 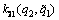can be written as follows:

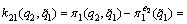
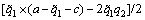     (22)

where 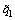 is the first-order belief of production strategy;  is the fair payment of leaders towards the followers, which is the average value of maximum and minimum benefit brought by the followers to the leaders under a given leaders’ production strategy and the followers’ production strategy q₂, namely,

     (23)

The goodwill degree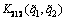of the leaders which is perceived by the followers can be described as the difference between the profit brought by theleaders’ production strategy to the followers and the average profit brought by the leaders to the followers, namely,

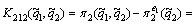
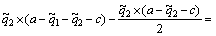
              (24)

where 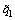 stands for the followers’ production belief under the condition of the first-order belief towards the leaders, i.e., 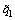is the second-order belief of the followers; 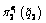is the fairness payment of the followers towards the leaders, which is the average value of maximum and minimum benefit brought to the leaders under a given followers’ production strategy belief and the followers’ production strategy belief 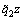, namely,

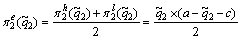     (25)

According to the above definition, the leaders’ utility function in preponderant high-tech metal mineral resources development compensation is

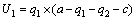                     (26)

While, the followers’ utility function can be written as

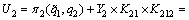
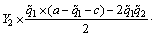
                 (27)

According to the solution of the Stackelberg game model, the first-order derivative of Eq. (27) is taken to obtain the optimal equilibrium production 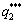, then using  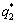in Eq. (26) to get the optimal production 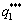, finally, the equilibrium solution of the sequential fairness preference Stackelberg model is

                     (28)

It can be concluded from Eq. (28) that in sequential equilibrium fairness preference Stackelberg model, sequential fairness Stackelberg equilibrium production is close to classic Cournot equilibrium production and the decrease in market production can enhance the degree of monopoly. According to the results of game experiment, the parties who have fairness preference and self-interest will interact, that is to say, fairness preference policy makers may make self-serving policy makers become more equitable when the former is in dominant; on the contrary, self-serving policy makers may make fairness preference decision-makers become selfish when they are in dominant. Therefore, when the followers are in sequential fairness condition, sequential fairness preference Stackelberg equilibrium may shift to Cournot equilibrium because fairness preference followers may make self-serving leaders become more equitable to split the market production. The decrease of the entire market capacity is because the followers will sacrifice their profits to punish self-serving leaders when inequity exists in the game.

4 Numerical simulation

4.1 Original basic parameter setting

According to the market supply and demand of lithium, antimony, indium, rare earth and the national industrial policy as well as the regression analysis of the Cournot linear demand function, the spontaneous demand stabilized at around 2000 t, so a in the Cournot model can take the value of 2000, namely a=2000, by analyzing the tax subjects of preponderant high-tech metal mineral resources development, namely the property cost (mineral resources compensation, resource tax), mining costs (outlay of exploration, outlay of mining), investment capital (capital investment per ton of mineral resources), production costs (raw materials, power costs, wages and benefits, manufacturing costs, processing fees, finance charges, operating expenses), security costs (safety training, disinfection equipment, risk assessment costs, occupational funds, pension), and part of the measurable environmetal governance operating costs (water pollution, air pollution, waste pollution, heavy metal pollution), environmetal restoration costs (mine land reclamation bond, tailings management costs, mine environmetal geology warning inputs). Based on tax subjects above and the statistical analysis of preponderant metal development compensation enterprises, the basic cost c of preponderant high-tech metal mineral resources development compensation enterprises is about 800 units.

4.2 Altruism preference coefficient impact

According to the relevant parameter assumptions of strategic price model and the action mechanism of altruism preference coefficient on Stackelberg equilibrium, the equilibrium quantity and the equilibrium price with the altruism preference coefficient ε of forerunner 1 are shown in Fig. 1.

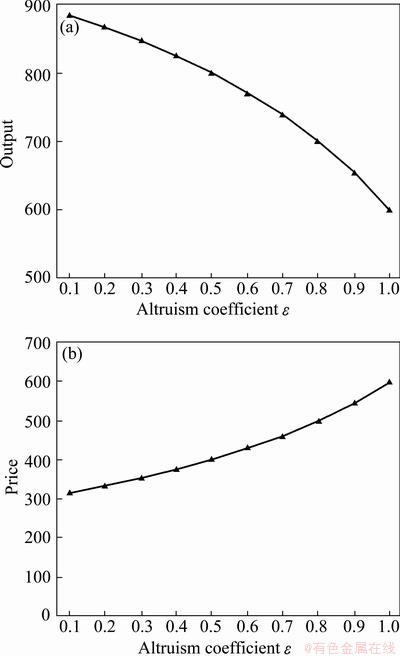
Fig. 1 Equilibrium quantity (a) and equilibrium price (b) variety with altruism preference coefficient ε of Oligarch 1

As can be seen from Fig. 1, the Stackelberg equilibrium quantity which considers altruistic preferences is less than the Stackelberg equilibrium quantity without considering altruistic preferences. The altruistic preferences oligarch leads to a higher monopoly degree of preponderant high-tech metal mineral resources oligopoly market. Figure 1 shows that Stackelberg equilibrium quantity increases as the degree of altruistic preferences reduces. And the price increases when the altruistic preference upgrades. The results are consistent with the theoretical model.

4.3 Inequity aversion coefficient impact

According to the analysis of the impact of inequity aversion coefficient on Stackelberg equilibrium, we assume that the inequity aversion coefficient of follower 2 in steady state is α₂=0.2. In this case, the equilibrium output and price varied with inequity aversion coefficient β₁ of Oligarch 1 is shown in Fig. 2.

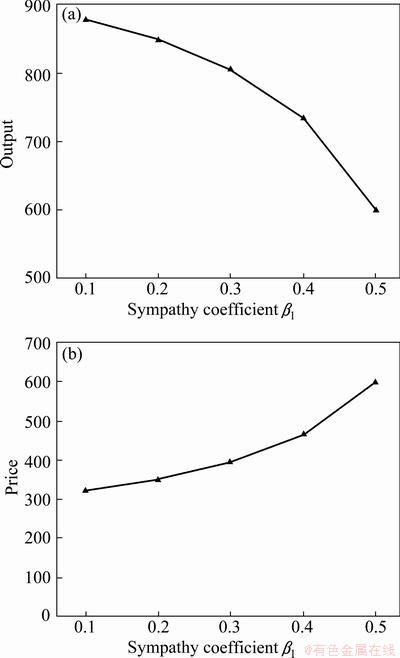
Fig. 2 Variation of equilibrium output (a) and price (b) with inequity aversion sympathy preferences coefficient β₁ of Oligarch 1

According to the analysis of the impact of inequity aversion coefficient on Stackelberg equilibrium, the inequity aversion coefficient of Oligopolist 1 in steady state is β₁=0.3. In this case, equilibrium output and price varied with the inequity aversion coefficient α₂ of Oligopolist 2 are shown in Fig. 3.

Fig. 3 Variation of equilibrium output (a) and price (b) with inequity aversion jealousy preferences coefficient α₂ of oligarchs 1

As can be seen from Figs. 2 and 3, the Stackelberg equilibrium output is less when taking inequity aversion into consideration. The inequity aversion oligarch leads to a higher monopoly degree market. When the inquity increases, Stackelberg equilibrium output increases. And when sympathy preference increases, the Stackelberg equilibrium output decreases. The results are consistent with the theoretical model. The inequity aversion Stackelberg equilibrium shows the characteristics of loss aversion.

5 Conclusions

By analyzing the revision of the reference value of compensation for preponderant high-tech metal mineral resources through social preferences equilibrium, quantifying the impact of interdependence preferences on the Stackelberg equilibrium and using numerical examples, the conclusion could be reached as follows. The higher the degree of altruism leaders of development for preponderant high-tech metal mineral resources, the more the market monopolized and vice versa. Under the condition of inequity aversion of preponderant high-tech metal mineral resources developers, the optimal reaction function and the standard Stackelberg equilibrium are both continuous, but the optimal reaction function that is inequity aversion of piecewise linearity is no longer monotonic, at the same time, the equilibrium output of inequity aversion leader and follower is less than the self-serving ones, so inequity aversion can enhance the degree of market monopoly; considering the decision-making of the sequential fairness Stackelberg equilibrium, the equilibrium production is close to classic Cournot equilibrium production and the decrease in market production can enhance the degree of monopoly. When taking social preferences in the development of preponderant high-tech metal mineral resources into consideration, the Stackelberg equilibrium market capacity decreases, owing to the importance and irreplaceability of preponderant high-tech metal mineral resources in national and industrial development, the price elasticity of demand for preponderant high-tech metal mineral resources is small, so the Stackelberg equilibrium decreases, oligopoly profits increases, i.e. oligopoly producers’ surplus increases, changes in the producer surplus is the strategic value that generated from Stackelberg game when considering social fairness preference. The above conclusion is that for the development and utilization of preponderant high-tech metal mineral resources compensation value, we should not only analyze from the perspective of the development and utilization of results, but also from the perspective of strategic interaction psychology, so the development and utilization of preponderant high-tech metal mineral resources compensation value system is no longer confined to economic value and ecological value, but also should include strategies value.

References

[1] EISENACK K, DENHOFER O, KALKUHL M. Resource rents: The effects of energy taxes and quantity instruments for climate protection [J]. Energy Policy, 2012, 48(9): 159-166.

[2] RASCH A, WAMBACH A, WIENER K. Bargaining and inequity aversion: On the efficiency of the double auction [J]. Economics Letters, 2012, 114(2): 178-181.

[3] GURTLER M, GURTLER O. Inequality aversion and externalities [J]. Journal of Economic Behavior & Organization, 2012, 84(1): 111-117.

[4] COX C A. Inequity aversion and advantage seeking with asymmetric competition [J]. Journal of Economic Behavior & Organization, 2013, 86(3): 121-136.

[5] TRUBY J. Strategic behaviour in international metallurgical coal markets [J]. Energy Economics, 2013, 36(3): 147-157.

[6] SANTOS-PINTO L. Making sense of the experimental evidence on endogenous timing in duopoly markets [J]. Journal of Economic Behavior & Organization, 2008, 68(3): 657-666.

[7] KOIDEA T, SANDOHB H. Economic analysis of an n-unit parallel redundant system based on a Stackelberg game formulation [J]. Computers & Industrial Engineering, 2009, 56(1): 388-398.

[8] CARDELLA E, CHIU R. Stackelberg in the lab: The effect of group decision making and “Cooling-off” periods [J]. Journal of Economic Psychology, 2012, 33(6): 1070-1083.

[9] BREITMOSER Y. On the endogeneity of Cournot, Bertrand, and Stackelberg competition in oligopolies [J]. International Journal of Industrial Organization, 2012, 30(1): 16-29.

[10] ZUBRICKAS R. How exposure to markets can favor inequity-averse preferences [J]. Journal of Economic Behavior & Organization, 2012, 84(1): 174-181.

[11] EISENKOPF G, TEVSSIER S. Envy and loss aversion in tournaments [J]. Journal of Economic Psychology, 2013, 34(2): 240-255.

[12] CATO S. The first-order approach to the principal–agent problems under inequality aversion [J]. Operations Research Letters, 2013, 41(5): 526-529.

[13] CASARI M, CASON T N. Explicit versus implicit contracts for dividing the benefits of cooperation [J]. Journal of Economic Behavior & Organization, 2013, 85(7): 20-34.

[14] BLANCO M, ENGELMAN D, NORMANN H T. A within-subject analysis of other-regarding preferences [J]. Games and Economic Behavior, 2011, 72( 2): 321-338.

[15] LI Zhen, MENG Qing-feng, SHENG Zhan-han. Revenue-sharing negotiation under time coordination based on fairness preference [J]. Systems Engineering-Theory & Practice, 2013, 1: 82-91.

[16] BI Gong-bing, QU An-ming, LIANG Qu. Supply chain coordination with wholesale price contract incorporating inequity aversion [J]. Systems Engineering-Theory & Practice, 2013, 1: 134-140.

优势高技术金属矿产资源的策略性均衡价格及数值模拟

钟美瑞^1,2，谌杰宇¹，朱学红^1,2，黄健柏^1,2

1. 中南大学 商学院，长沙 410083；

2. 中南大学 金属资源战略研究院，长沙 410083

摘  要：针对优势高技术金属矿产资源开发补偿价值体系及定价机制的扭曲，构建社会效用函数修正优势高技术金属矿产资源开发商决策效用函数，并把社会效用函数延伸到优势高技术金属矿产资源开发的斯坦克尔伯格产出决策博弈模型中。分析利他、非公平厌恶及序贯互动公平信念均衡对市场垄断程度的影响，进而分析产量与价格的变动趋势，并获得具有实验经济学意义的博弈公平均衡。通过数值模拟对博弈公平均衡进行算例验证。首次提出用生产者剩余变化来测度心理偏好产生的策略性价值的测度方法，为优势高技术金属矿产资源开发补偿价值体系完善提供技术支撑。

关键词：金属；高技术矿产；矿产资源；均衡价格；数值模拟

(Edited by Sai-qian YUAN)

Foundation item: Project (13&ZD024) supported by Major Program of the National Social Science Foundation of China; Projects (13YJAZH149, 09YJC90261) supported by the Ministry of Education Humanities and Social Sciences Foundation of China; Project (20110491264) supported by Postdoctoral Foundation of China; Project (S2011R1040) supported by Postdoctoral Research Funding Special Project of Hunan Province, China; Project (2011RWSK016) supported by Central South University Science Research Foundation Humanities Social Sciences Outstanding Young Talent Special Funding

Corresponding author: Xue-hong ZHU; Tel: +86-731-88879595; E-mail: zhxh@mail.csu.edu.cn

DOI: 10.1016/S1003-6326(13)62846-0