DOI: 10.11817/j.issn.1672-7207.2016.01.029
基于TOPSIS-FCA的预应力锚索失效风险评价
李云1, 2,刘霁2, 3
(1. 汕头大学 土木工程系,广东 汕头,515063;
2. 湖南城建职业技术学院,湖南 湘潭,411100;
3. 中南大学 资源与安全工程学院,湖南 长沙,410083)
摘要:为了对预应力锚索失效风险分级,利用逼近于理想TOPSIS的方法,选取岩石单轴抗压强度、外锚结构合理度、锚筋实际长度与设计长度之比、灌浆饱和度、锚索腐蚀程度、预应力损失率共6项指标对待评价对象进行风险等级评价。通过计算指标分类标准和待评价对象的相对贴近度,得到风险等级标准的相对接近度范围并对待评价对象进行风险等级评价。将评价结果与神经网络预测结果进行对比,利用灰色关联理论计算各评价指标与风险评价结果的关联性,并用形式概念分析(FCA)对指标进行核属性搜索,找出风险评价时必不可少的指标。研究结果表明:利用TOPSIS-FCA的方法能对预应力锚索失效风险进行评价,该评价模型对预应力锚索支护工作有一定的参考价值。
关键词:预应力锚索;风险评价;形式概念分析;灰色关联理论
中图分类号:TD05 文献标志码:A 文章编号:1672-7207(2016)01-0210-08
Failure risk evaluation of prestressed anchorage cable based on TOPSIS-FCA
LI Yun1, 2, LIU Ji2, 3
(1. Department of Civil Engineering, Shantou University, Shantou 515063, China;
2. Hunan Urban Construction College, Xiangtan 411100, China;
3. School of Resources and Safety Engineering, Central South University, Changsha 410083, China)
Abstract: In order to classify failure risk of prestressed anchorage cable, a method for order preference by similarity to ideal solution (TOPSIS) was used to conduct the risk evaluation of six indexes, i.e. uniaxial compressive strength, reasonable structure of the outer anchor, and the anchor bar ratio of actual length and design length, filling saturation, the degree of corrosion anchor and the prestressed loss rate. By calculating the relative closeness of the indexes classification standards and objects to be evaluated, the relative closeness range of risk level standards were obtained and the risk level of object was evaluated. The gray correlation theory was used to calculate correlation between each evaluation indicator and risk evaluation result, and the formal concept analysis (FCA) was used to search core attribution to find the essential indicators. The results show that TOPSIS-FCA method can evaluate the failure risk of prestressed anchorage cable, and that the evaluation model has reference value to prestressed anchorage cable support.
Key words: prestressed anchorage cable; risk evaluation; formal concept analysis; gray correlation theory
岩土工程灾害越来越受到人们的重视。预应力锚索具有扰动小、施工快速高效等特点,因此,被作为一种重要的加固方式而广泛应用于地下矿山巷道、露天边坡、基坑等工程中[1-2]。由于受预应力锚索工作的环境和自身工程质量等因素的影响,在实际工程中经常会出现锚索失效的情况,并引发岩土失稳等一系列灾害问题,这会造成巨大的经济损失和人员伤亡。在锚索失效风险评价方面,多数研究者重点研究岩土工程自身稳定性,然后利用距离判别法、粗集、可拓学等评价方法对岩土自身的稳定性进行评价[3-4],而对预应力锚索自身失效风险评价的研究较少。胡洪英[5]利用物元分析对预应力锚索失效进行风险评估,但并没有利用失效风险等级标准的评价分析指标与评价结果之间的关系,使得其评价效果较差。为此,本文作者利用逼近于理想的技术TOPSIS首先对包括失效风险等级标准在内的预应力锚索失效风险进行评价[6],通过比较待评价对象的相对接近度,得到相应的失效风险等级,并对待评价对象的失效风险程度进行排序;然后利用灰色关联理论对影响预应力锚索失效的因素进行关联分析,得到各影响因素与预应力锚索失效风险间的关联性,同时利用形式概念分析找出评价时不可缺少的指标,完善对预应力锚索失效的风险评价。
1 TOPSIS的基本思想
TOPSIS的基本思想[7]是找出决策问题的理想解和负理想解,即最好的和最差的2个解,然后对待评价方案进行计算,其中既与理想解的距离最近且与负理想解的距离最远的方案为最佳方案。
理想解是假定的最佳方案,一般要求理想解所对应的各属性值至少达到各待评价方案中的最好值;负理想解是假定最差方案,一般要求负理想解所对应的各属性值至少不优于各待评价方案中的最差值。一般来说,待评价方案往往不止1个。为了对待评价方案的优劣进行评价,通过对各待评价方案与理想解及负理想解的距离进行比较,对评价方案进行优劣排序。设决策方案有m个目标fj(j=1, 2, …, m)和n个可行方案xi(i=1, 2, …, n),经规范化加权,目标的理想解为Z *,Z*=(Z 1*, …, Z m*)T;负理想解为Z-=( Z1-, …, Zm-)T。用欧几里得范数作为距离的测度,则待评价方案到理想解Z *的距离Si*和到负理想解的距离Si-分别为:
 ;i=1, 2, …, n (1)
;i=1, 2, …, n (1)
 ;i=1, 2, …, n (2)
;i=1, 2, …, n (2)
其中:Zij为第j个目标对第i个待评价方案的规范化加权值。则某一待评价方案对于理想解的相对接近度为
 ;0≤Ci*≤1;i=1, 2, …, n (3)
;0≤Ci*≤1;i=1, 2, …, n (3)
显然,若xi为理想解,则相应的Ci*=1;若xi为负理想解,则相应的Ci*=0。待评价方案xi越靠近理想解,则相对接近度Ci*越接近于1。通过计算各待评价方案的相对贴近度即可对所有方案优劣进行排序。
2 理想点与形式概念分析的预应力锚索失效风险评价模型
2.1 预应力锚索失效风险评价指标的选取
影响预应力锚索失效的指标很多,参考有关预应力锚索失效因素的分析研究[8-12],结合实际情况并考虑主要影响因素,选取外锚结构合理度、锚筋实际长度与设计长度之比、灌浆饱和度、锚索腐蚀程度、预应力损失率作为预应力锚索失效指标。除了以上锚索自身的工程质量外,工程岩体质量也对锚固工程有较大影响,所以,选取岩体单轴抗压强度作为影响因素之一。根据相关评价标准,这6个参数指标等级标准如表1所示。
表1 单因素指标分级标准
Table 1 Classification standards with single factorial index

表1中:Ⅰ级表示预应力锚索“失效风险极小”;Ⅱ级表示“失效风险小”;Ⅲ 级表示“失效风险中等”;Ⅳ 表示“失效风险较大”;Ⅴ级表示“失效风险大”。
2.2 决策矩阵的规范化
由于不同指标的数值差异很大,为了便于计算,需将多目标问题的决策矩阵规范化。规范化的决策矩阵为 ,矩阵中的元素为
,矩阵中的元素为 。
。
 ;i=1, 2, …, n;j=1, 2, …, m (4)
;i=1, 2, …, n;j=1, 2, …, m (4)
其中:fij为原决策矩阵中的元素。为了对待评价方案进行风险分级,在计算时将单因素指标分类标准与待评价方案集合并成1个矩阵,同时也对待评价方案进行风险排序。
2.3 指标权重的确定
在风险评价中,各指标对失效风险等级的影响作用各不相同。为减少权重的主观性影响,可根据指标失效风险贡献率计算各指标权值。
 ;
; (5)
(5)
其中:wi为第i种指标的权值;ai为第i种因素的实测平均值; 为第i中因素各级标准的平均值;m为指标个数。
为第i中因素各级标准的平均值;m为指标个数。
2.4 规范化加权矩阵的构造
通过将权重矩阵与规范化的矩阵相乘,建立规范化的加权矩阵Z,矩阵元素为Zij。
 ;i=1, 2, …, n;j=1, 2, …, m (6)
;i=1, 2, …, n;j=1, 2, …, m (6)
2.5 指标评价标准和待评价方案的相对接近度的计算
根据单因素指标分类标准,确定的方案的理想点与负理想点。利用式(1)~(3)计算规范化的加权矩阵中各方案接近理想点的相对接近度。通过对比待评价方案与分类标准的相对接近度,对待评价方案的失效风险等级进行评价,并根据相对接近度排序。
2.6 灰色关联分析
通过对待评价方案进行风险评价,得到完整的评价决策矩阵。为了分析各指标对评价决策的重要性,利用灰色关联理论对其重要性进行相关分析。在完整的评价决策矩阵中,各指标值差异较大,需对其进行量纲一化。指标中含有2类:一类是值越大,方案越好;另一类是值越小,方案越好。其计算公式分别 如下。
值越大方案越好的指标:
 (7)
(7)
值越小方案越好的指标:
 (8)
(8)
2.7 形式概念分析的核属性搜寻
形式概念分析又称为概念格。1个形式背景K=(G,M,I)由对象集合G、属性集合M和二者之间的关系I组成。对于1个形式背景的对象集A∈p(G),属性集B∈p(M)定义以下映射f和g:
 ,
,

则从形式背景中得到的每一个满足以上2个映射的二元组(A,B)为1个概念,A称为概念(A,B)的外延,B为概念(A,B)的内涵。对于概念(A1,B1)和(A2,B2),若满足 或
或 ,则称(A1,B1)为子概念或亚概念,(A2,B2)为父概念或超概念。由形式背景中所有超概念-亚概念的偏序关系所诱导出的格即为概念格[13-15]。基于概念格的核属性搜索的基本思想是通过构建一个完整的概念格,求出其中的相融可辨概念及其亏属性。亏属性的最简形式为不可约简的最简化形式[16],其中单个属性集即为核属性。
,则称(A1,B1)为子概念或亚概念,(A2,B2)为父概念或超概念。由形式背景中所有超概念-亚概念的偏序关系所诱导出的格即为概念格[13-15]。基于概念格的核属性搜索的基本思想是通过构建一个完整的概念格,求出其中的相融可辨概念及其亏属性。亏属性的最简形式为不可约简的最简化形式[16],其中单个属性集即为核属性。
若2个对象概念( A1,B1)和(A2,B2)共有1个父概念( A,B),且该父概念(A,B)的内涵中不包含决策属性,但 ∨
∨ ,则称该公共父概念(A,B)为概念(A1,B1)和(A2,B2)的相融可辨概念(其中VD为决策属性集)。对于概念(A,B),若原决策表中的条件属性
,则称该公共父概念(A,B)为概念(A1,B1)和(A2,B2)的相融可辨概念(其中VD为决策属性集)。对于概念(A,B),若原决策表中的条件属性 满足
满足 ,则满足此条件的所有条件属性
,则满足此条件的所有条件属性 的集合称为概念(A,B)相对于初始决策表的亏属性。基于TOPSIS-FCA的预应力锚索失效风险评价模型见图1。
的集合称为概念(A,B)相对于初始决策表的亏属性。基于TOPSIS-FCA的预应力锚索失效风险评价模型见图1。
3 工程应用
某一地下矿山使用预应力锚索对围岩进行初步支护。为了检查支护效果,保证围岩支护的安全,对预应力锚索失效风险进行评价。根据支护位置的表征样貌,对几处有代表性的位置进行无损采样检测,其参数见表2。
3.1 数据规范化
由于所选取参数的值具有较大差异性,利用式(4)对数据进行规范化。TOPSIS一般用于对待评价方案进行排序。为了能够根据分级标准对待评价对象进行风险等级评价,所以将单因素指标分级标准与待评价对象同时规范化,可以很容易找到理想解与负理想解,其中理想解即为Ⅰ级中的最优值,负理想解为Ⅴ级中的最差值。经过规范化后的结果见表3。

图1 TOPSIS-FCA的预应力锚索失效风险评价模型
Fig. 1 Failure risk evaluation model of prestressed anchorage cable based on TOPSIS-FCA
从表3可以看出:规范化后的理想解为(0.615, 0.296, 0.300, 0.291, 0, 0);负理想解为(0, 0, 0, 0, 0.981, 0.703)。
3.2 确定指标权重
各指标对评价结果影响的程度不同,所以,应该确定各指标的权重。对于不同的地质环境,指标权重也不相同。为排除人为主观对权重的影响,应根据各指标的作用程度分别赋予不同的权重。根据实际环境中各指标对预应力锚索失效风险贡献率确定权重,利用式(5)和(6)确定的各指标权重,见表4。
从表4可以看出:在该区域内,外锚结构合理度权重最大,说明外锚结构合理度较其他指标的变化较大;锚索腐蚀程度权重最小,说明锚索腐蚀程度较其他指标的变化较小。
表2 待评价对象参数
Table 2 Objects of to be evaluated parameters

表3 数据规范化
Table 3 Data normalization
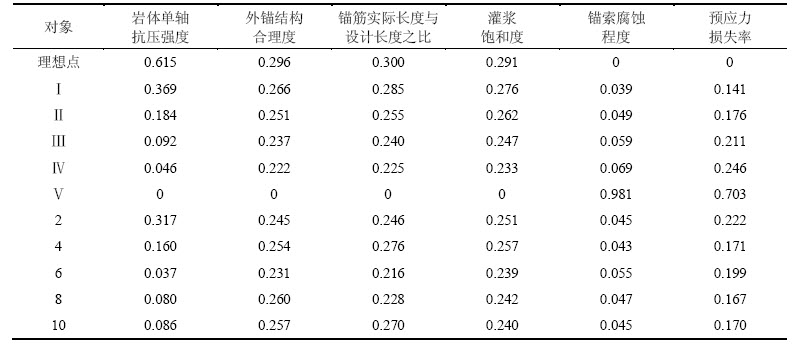
表4 评价指标
Table 4 Evaluation parameters

3.3 相对接近度的计算
结合指标权重,可以得到规范化加权目标的理想解Z*=(0.109, 0.061, 0.059, 0.058, 0, 0),负理想解是Z-=(0, 0, 0, 0, 0.065, 0.111)。通过式(7)对表3中的数据进行加权计算,然后利用式(1)~(3),得到每个对象与理想解、负理想解的距离,最后得到各对象接近理想点的相对接近度,见表5。
从表5可以看出:理想解的相对接近度为1,负理想解的相对接近度为0。预应力锚索失效风险评价的相对接近度分类如下:对于Ⅰ级失效风险,0.762≤Ci*≤1;对于Ⅱ级失效风险,0.630≤Ci*<0.762;对于Ⅲ级失效风险,0.566≤Ci*<0.630;对于Ⅳ级失效风险,0.526≤Ci*<0.566;对于Ⅴ级失效风险,0≤Ci*<0.526。根据以上相对接近度分类标准及各待评价对象的相对接近度,可对待评价对象进行风险评价,评价结果见表5。
从表5可以看出:对象1,2,3,4,5和9的评价结果为Ⅱ级,即“失效风险小”;对象7,8和10的评价结果为Ⅲ级,即“失效风险中等”;对象6的评价结果为Ⅳ级,即“失效风险较大”。为了验证评价结果的可靠性,将TOPSIS与神经网络预测的结果进行对比。通过对表3中的前6条评价规则数据进行训练,然后对6条评价规则和10个待评价对象进行预测。16个对象的BP预测结果及二者对比结果见图2及表6。
表6中的神经网络预测数据是由图2中的预测数据向上取整得到。表6中2种方法的评价结果一致,说明通过TOPSIS对锚索失效风险等级评价是可行的。
3.4 灰色关联与形式概念分析
3.4.1 灰色关联分析
由于各指标对评价决策的重要性不同,利用灰色关联理论对评价指标进行重要性分析。将表5中的10个待评价对象的6项评价指标及评价结果的数据提取出来,但指标值差异较大,且指标数据对评价结果的影响分为越大越好和越小越好2类,用式(8)和(9)对其进行量纲一化,见表7。

图2 BP神经网络预测结果
Fig. 2 BP neural network prediction results
利用量纲一化后的数据进行关联度计算,计算后的指标关联度见表8。
从表8可以看出:岩体单轴抗压强度的关联度最大,且比锚索的工程质量指标的关联度都大,说明工程岩体质量与预应力锚索失效风险的同步变化趋势最接近,即工程岩体质量对预应力锚索失效风险影响最大;在锚索的工程质量指标中,该矿区的灌浆饱和度对预应力锚索失效风险影响最大,外锚结构合理度、锚筋实际长度与设计长度之比对风险评价也有较大影响,而预应力损失率对风险评价影响较小,在今后的支护工作中,应据此突出工作重点。
3.4.2 决策表的形式概念分析
在对某件事物进行评价时,有些因素或许不是最重要却又是不可缺少的。为了找出各指标与评价结果之间的这种内在关系,利用概念格理论对决策矩阵进行分析。概念格在进行约简时,能够将指标与评价结果联系起来,而不仅仅是约简掉重复的信息。通过对决策矩阵进行指标约简,约简得到的是1个属性或几个约简结果的共有属性,即所有的单个属性集,则核属性指标为在对预应力锚索失效风险进行评价时必不可少的指标。为了进行形式概念分析,首先将评价指标及评价结果用相应的分级语言代替具体数值,见表9。
形式概念分析的对象是具体的形式背景,所以,将表9转换为1个形式背景,见表10。
表5 预应力锚索失效风险TOPSIS-FCA 模型评价结果
Table 5 Results of failure risk evaluation of prestressed anchorage cable using TOPSIS-FCA model

表6 TOPSIS与BP神经网络评价结果比较
Table 6 Comparison of results from TOPSIS and BP neural network evaluation

表7 量纲化一的预应力锚索参数
Table 7 Prestressed anchorage cable dimensionless parameters

表8 指标关联度
Table 8 Indexes correlativeness

表9 预应力锚索知识表达系统
Table 9 Knowledge expression system of prestressed anchorage cable

表10 形式背景
Table 10 Formal context

形式背景具有单值特征,它根据各属性的不同取值,转换为某一属性的某一取值即一种属性的形式背景,如表9的岩石单轴抗压强度指标有Ⅱ,Ⅲ,Ⅳ和Ⅴ共4种取值,其形式背景中就有4个该指标的属性。
据Hasse图,表9中有5个待评价对象的外锚结构合理度和锚索腐蚀程度的等级为Ⅱ。该Hasse图中共有39个节点,即39个概念。通过观察父概念与子概念的关系,可以找到以下12个相融可辨概念:({1,2,…,10},{ });({3,5,6},{f3});({1,5,6},{e3});({6,8,10},{d4});({1,3,4,5,7,10},{c2});({2,4,7,9},{d3,e2});({1,4,7,10},{c2,f2});({5,6},{e3,f3});({4,7,9},{b2,d3,e2});({4,7,8,10},{b2,e2,f2});({4,7,10},{b2,c2,e2,f2});({4,7}, {b2,c2,d3,e2,f2})。
});({3,5,6},{f3});({1,5,6},{e3});({6,8,10},{d4});({1,3,4,5,7,10},{c2});({2,4,7,9},{d3,e2});({1,4,7,10},{c2,f2});({5,6},{e3,f3});({4,7,9},{b2,d3,e2});({4,7,8,10},{b2,e2,f2});({4,7,10},{b2,c2,e2,f2});({4,7}, {b2,c2,d3,e2,f2})。
由相融可辨概念可得到它的亏属性为
{a b c d e f, a b c d e, a b c d f, a b c e f, a b d e f, a b c f, a b d e, a b c d, a c f, a c d, a d, a}
亏属性集合中的每个元素都是不可同时约简的,并且当某一属性是不可约简时,它的超集必不可约简,所以,属性a即岩石单轴抗压强度是不可约简属性集合的最简化形式,且为核属性。因此,在对预应力锚索失效风险进行评价时,岩体单轴抗压强度是不可缺少的指标。一般而言,工程岩体质量在很大程度上决定了支护方法。在对预应力锚索失效风险进行评价时,工程岩体质量仍然是支护效果评价的关键因素,支护失效的最终表现形式还是岩体的破坏,这与实际相符。
4 结论
1) 利用逼近于理想的方法,计算单因素指标等级分类和待评价对象的相对接近度,这样不仅能够根据待评价对象的相对接近度对预应力锚索失效风险进行排序,而且能根据单因素指标等级分类的相对接近度的范围对待评价对象的风险等级进行评判;同时,将评价结果与BP神经网络的评价结果进行对比,二者评价结果一致,说明TOPSIS评价具有可靠性。
2) 通过灰色关联理论计算各指标对风险评价结果的相对重要程度,可找到各评价指标对结果的影响程度。其中岩石单轴抗压强度指标最重要,该指标对预应力锚索失效风险评价影响最大,这与实际相符;在工程质量方面,灌浆饱和度对预应力锚索失效风险评价影响最大,外锚结构合理度、锚筋实际长度和设计长度之比对评价结果也具有较大影响。所以,对该矿区进行支护工作时,应加强注浆、外锚物和锚筋长度选择等工作,增强支护效果。
3) 形式概念分析在约简时能够同时考虑条件属性与决策属性,而不仅仅是考虑条件属性并排除冗余信息。对预应力锚索失效风险进行评价时,岩石单轴抗压强度指标为必要指标,即工程岩体质量是不可缺少的评价指标。这是因为工程岩体质量直接影响了岩体的稳定性,无论如何改变支护方法,工程岩体质量仍是支护工作最基础的参数,这与实际情况相符。
参考文献:
[1] 张志亮. 预应力锚索耐腐蚀性及失效研究[D]. 北京: 中国地质大学工程技术学院, 2008: 1-2.
ZHANG Zhiliang. The research of prestressed anchorage cable[D]. Beijing: China University of Eeoscience. School of Engineering and Technology, 2008: 1-2.
[2] 刘世锋. 预应力锚索在何群峡段危岩体整治工程中的应用[J]. 岩石力学与工程学报, 2003, 22(S2): 2734-2737.
LIU Shifeng. Application of prestressed anchor cable to control engineering of unstable rockmasses in Hequnxia experimental section[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(S2): 2734-2737.
[3] 岩小明, 李夕兵, 陈祥云. 基于距离判别分析理论的露天矿边坡潜在破坏模式识别方法[J]. 中国安全科学学报, 2012, 22(8): 124-130.
YAN Xiaoming, LI Xibing, CHEN Xiangyun. A distance discriminant analysis method for identifying open-pit slope potential failure mode[J]. China Safety Science Journal, 2012, 22(8): 124-130.
[4] 李云, 刘霁. 基于RS-CPM模型的边坡失稳灾害预测及应用[J]. 中南大学学报(自然科学版), 2013, 44(7): 2971-2976.
LI Yun, LIU Ji. Slope instability disaster forecast and its application based on RS-CPM model[J]. Journal of Central South University (Science and Technology), 2013, 44(7): 2971-2976.
[5] 胡洪英. 基于物元分析的预应力锚索失效风险评价方法[J]. 西部交通科技, 2012(10): 27-31.
HU Hongying. Failure risk evaluation method of prestressed anchorage cable based on matter-element analysis[J]. Western China Communications Science & Technology, 2012(10): 27-31.
[6] 胡建华, 尚俊龙, 雷涛. 基于RS_TOPSIS法的地下工程岩体质量评价[J]. 中南大学学报(自然科学版), 2012, 43(11): 4412-4419.
HU Jianhua, SHANG Junlong, LEI Tao. Rock mass quality evaluation of underground engineering based on RS-TOPSIS method[J]. Journal of Central South University (Science and Technology), 2012, 43(11): 4412-4419.
[7] 方国华, 黄显峰. 多目标决策理论、方法及其应用[M]. 北京: 科学出版社, 2011: 77-82.
FANG Guohua, HUANG Xianfeng. Multi-objective decision theory and its application[M]. Beijing: Science Press, 2011: 77-82.
[8] 李英勇, 张顶立, 张宏博, 等. 边坡加固中预应力锚索失效机制与失效效应研究[J]. 岩土力学, 2010, 31(1): 144-150.
LI Yingyong, ZHANG Dingli, ZHANG Hongbo, et al. Research on failure mechanism and effects of prestressed anchor cables for reinforcing slopes[J]. Rock and Soil Mechanics, 2010, 31(1): 144-150.
[9] 郑静, 朱本珍. 边坡锚索结构的失效因素与破坏类型[J]. 铁道工程学报, 2010(1): 10-13.
ZHENG Jing, ZHU Benzhen. Failure factor and failure damage type of slope anchor structure[J]. Journal of Railway Engineering Society, 2010(1): 10-13.
[10] 李波. 边坡预应力锚索安全评价指标研究[D]. 重庆: 重庆大学土木工程学院, 2012: 14-28.
LI Bo. Study on safety evaluation index of slope prestressed anchor cable[D]. Chongqing: Chongqing University. College of Civil Engineering, 2012: 14-28.
[11] 刘红军, 李洪江. 基于能量法的锚杆失效模糊判别方法研究[J]. 岩土工程学报, 2013, 35(8): 1435-1441.
LIU Hongjun, LI Hongjiang. Fuzzy identification method for failure of anchors based on energy principle[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(8): 1435-1441.
[12] 陈奕奇, 郭红仙, 宋二祥, 等. 岩土锚固结构腐蚀程度的评估[J]. 岩石力学与工程学报, 2007, 26(7): 1492-1498.
CHEN Yiji, GUO Hongxian, SONG Erxiang, et al. Corrosion evaluation for existing ground anchored structure[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(7): 1492-1498.
[13] 李云. 概念格分布处理及其框架下的知识发现研究[D]. 上海: 上海大学计算机科学与工程学院, 2005: 7-17.
LI Yun. Research on distributed treatment of concept lattices and knowledge discovery based on its framework[D]. Shanghai: Shanghai University. School of Computer Science and Engineering, 2005: 7-17.
[14] DIAS S, LUISE Z, VIEIRA N. Using iceberg concept lattices and implications rules to extract knowledge from ANN[J]. Intelligent Automation & Soft Computing, 2013, 19(3): 361-372.
[15] MA Jianmin, ZHANG Wenxiu. Axiomatic characterizations of dual concept lattices[J]. International Journal of Approximate Reasoning, 2013, 54(5): 690-697.
[16] 杨凯, 马垣. 基于概念格的多层属性约简方法[J]. 模式识别与人工智能, 2012, 25(6): 922-927.
YANG Kai, MA Yuan. Multi-level attribute reduction methods based on concept lattice[J]. Pattern Recognition and Artificial Intelligence, 2012, 25(6): 922-927.
(编辑 陈灿华)
收稿日期:2015-01-12;修回日期:2015-03-22
基金项目(Foundation item):国家自然科学基金资助项目(50774092);湖南省科技计划项目(2011SK3128);湖南省高等学校科学研究项目(13C104) (Project(50774092) supported by the National Natural Science Foundation of China; Project(2011SK3128) supported by the Science and Technology Plan of Hunan Province; Project(13C104) supported by the Science Research of Higher School of Hunan Province)
通信作者:刘霁,博士,教授,从事土木工程施工技术与施工管理的研究;E-mail: liyunliuji@163.com