J. Cent. South Univ. (2017) 24: 2105-2113

DOI: https://doi.org/10.1007/s11771-017-3619-1

Rock burst prediction based on genetic algorithms and extreme learning machine

LI Tian-zheng(李天正), LI Yong-xin(李永鑫), YANG Xiao-li(杨小礼)

School of Civil Engineering, Central South University, Changsha 410075, China

Central South University Press and Springer-Verlag GmbH Germany 2017

Abstract: Rock burst is a kind of geological disaster in rock excavation of high stress areas. To evaluate intensity of rock burst, the maximum shear stress, uniaxial compressive strength, uniaxial tensile strength and rock elastic energy index were selected as input factors, and burst pit depth as output factor. The rock burst prediction model was proposed according to the genetic algorithms and extreme learning machine. The effect of structural surface was taken into consideration. Based on the engineering examples of tunnels, the observed and collected data were divided into the training set, validation set and prediction set. The training set and validation set were used to train and optimize the model. Parameter optimization results are presented. The hidden layer node was 450, and the fitness of the predictions was 0.0197 under the optimal combination of the input weight and offset vector. Then, the optimized model is tested with the prediction set. Results show that the proposed model is effective. The maximum relative error is 4.71%, and the average relative error is 3.20%, which proves that the model has practical value in the relative engineering.

Key words: extreme learning machine; feed forward neural network; rock burst prediction; rock excavation

1 Introduction

Rock burst refers to the rock’s brittle failure accompanied with the phenomenon of peeling, cracking and even throwing. The common failure criterion for evaluation is nonlinear in geotechnical and mining engineering [1-4], and the rock masses follow it with nonlinear envelope. It often occurs when elastic potential energy gathered in the rock is violently released because of chamber excavation and other activities. It is a common kind of engineering geological disaster in underground rock excavation of high stress areas. Rock burst has occurred in engineering, causing a large number of casualties and economic losses. With the rapid development of China’s water conservancy and hydropower, transportation, deep mining and other undertakings, more and more constructions are exposed to high stress rock mass excavation. Therefore, the issue of rock burst prediction and prevention in engineering is particularly important.

Researchers try to predict rock burst from different aspects based on rock burst mechanism. Currently theoretical researches mainly includes fuzzy mathematics [5], catastrophe theory [6], BP neural network [7, 8] and support vector machine [9, 10], which have received good results to some extent. However, there always exist problems in these methods described above, such as subjectivity, large dependence on experience, lack of precision, too complicated parameter settings. Extreme learning machine (ELM) model is proposed in [11, 12]. It is a supervised learning algorithm. It aims at improving the defects of slow training, low precision and poor generalization performance existing in single hidden layer feedforward neural network (SLFNs), which can compensate well for the defects of above methods. In view of those, according to the principle of extreme learning machine, maximum shear stress, uniaxial compressive strength, uniaxial tensile strength and rock elastic energy index were selected as the input factors [13], and burst pit depth as output factor. Then, genetic algorithm (GA) is adopted to optimize the relevant parameters. The genetic algorithms and extreme learning machine (GA-ELM) rock burst prediction model is proposed to predict the intensity of rock burst in engineering [14].

2 Theoretical models

2.1 Input factor

The prediction accuracy of the model is closely related to the input factors which must be able to fully and truly reflect the factors affecting rock burst. As the premise of the establishment of the model, determination of the input factors plays a crucial role and must be based on an in-depth analysis of the formation mechanism of rock burst. In recent decades, many scholars have studied the formation mechanism of rock burst in detail, and put forward a variety of discrimination indicators, including rock stress indicator, energy indicator [15], brittleness coefficient indicator and stiffness indicator. Those definitions and criteria are shown in Table 1. Although the stiffness indicator is a clear physical concept, but for rock, it is difficult to directly calculate the rock stiffness with only a few exceptions. As a result, it is not listed in Table 1.

Symbols in Table 1 have the following meanings. σ_c is the rock uniaxial compressive strength, σ_max is the maximum geostress, σ_t is the rock uniaxial tensile strength, Φ_sp and Φ_st represent elastic strain energy release and elastic strain energy loss in rock unloading respectively which can be seen in Fig. 1, E_t is the kinetic energy of rock debris when thrown out in rock uniaxial compression test, E_s is the maximum elastic strain energy stored in rock, F₁ and F₂ represent the area under the curve before and after the peak of the rock complete stress-strain curve respectively which can be seen in Fig. 2.

There exist certain defects when using the above indicators to judge the rock burst. For example, stress indicator is on the basis of strength theory with a starting point of static equilibrium conditions, and stress strength is considered as the criterion of rock burst. Therefore, it cannot accurately explain the rock ejection mechanism, which is a dynamic process. Likewise, energy indicator is based on energy theory, which can solve the problem of energy source of rock burst and well explain the earthquake, rock ejection and other dynamic phenomena from the viewpoint of energy. But the theory does not take into account the factors of time and space, which is needed to be developed. Lastly, rock brittleness coefficient indicator singly considers the uniaxial compressive strength and uniaxial tensile strength, which only specifies the characteristics of rock itself. But it lacks enough consideration of stress and strain situation of country rock. So, its accuracy can hardly be guaranteed.

In summary, the following discussions are obtained. 1) Factors affecting rock burst can be summarized as internal and external ones. Internal factors mainly refer to the high stress of country rock, brittle failure and rock energy storage. External factors mainly refer to the rock stress unloading and redistribution due to the excavation. 2) The above criteria are all based on one single indicator to judge the occurrence of rock burst. In fact, rock burst is influenced by many factors which are closely linked with each other and indivisible. Meanwhile one factor’s influence on rock burst will vary depending on the engineering characteristics. Thus, multi-index model in rock burst prediction is more persuasive.

With a comprehensive measurement and synthetic evaluation, as well as to facilitate the theoretical analysis and numerical calculation, maximum shear stress σ_θ, uniaxial compressive strength σ_c, uniaxial tensile strength σ_t and rock elastic energy index W_et are selected as the input factors. σ_θ reflects the rock stress level after excavation, indirectly reflecting the high stress of country rock. σ_c and σ_t reflects the mechanical properties of the rock respectively, which is the discrimination of rock’s brittle failure. W_et reflects the elastic energy storage in rock. The four indicators can fully summarize the factors affecting rock burst.

2.2 Output factor

Output factor of the model is the most direct expression of the rock burst grade, whose determination has an important impact on the accuracy of the model. Currently graded approaches of rock burst are qualitatively developed based on the external characteristics of the rock after burst. In the network model, the output is a value. As a result, it is unable to correspond with the qualitative rock burst grades. So, an indicator is needed to be found which not only can fully reflect the intensity of rock burst, but also can be quantitatively analyzed.

Rock burst characteristics [16] include sound features, burst-off rock features, burst pit and burst surface features. The rock has the nonlinearity when the failure occurs [17-19], and it follows the nonhomogenity and nonassoated flow rule [20, 21]. In the process of rock burst, there always appear varying degrees of rock peeling, falling and even massive ejections accompanied with the phenomenon of acoustic emission. After that, the rock burst grades can be determined by observing the features of burst-off rock, burst pit depth and burst surface. Lots of practical experience has shown that compared with the other features, burst pit depth is more readily available, and more truly reflects the intensity of rock burst with less interference by other factors. For these reasons, burst pit depth is identified as the output factor, which is indicated by the symbol t. It is worth noting that structural surfaces with different occurrence and scale have a certain influence on burst pit depth, which may lead the predictions largely deviating from the actual results [22]. The rock peeling, massive falling, ejection and burst pit depth are illustrated in Figs. 3 to 6.

Table 1 Indicators and criteria of rock burst

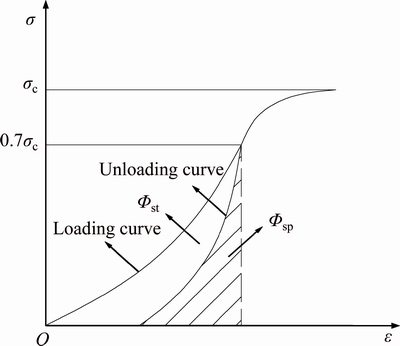
Fig. 1 Elastic energy index W_et (W_et=Φ_sp/Φ_st)

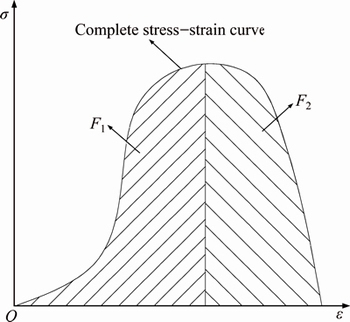
Fig. 2 Impact energy index W_CF (W_CF=F₁/F₂)

According to the characteristics of the GA-ELM model, meanwhile referring to the existing classification standards, rock burst grades are divided into the following five categories. There are grade I (no rock burst), grade II (slight rock burst), grade III (moderate rock burst), grade IV (strong rock burst) and grade V (very strong rock burst) [23, 24]. Corresponding relations among rock burst grade, the main phenomena and characteristics, burst pit depth t are shown in Table 2.

Fig. 3 Rock peeling

Fig. 4 Massive falling

Fig. 5 Rock ejection

Fig. 6 Burst pit depth

Table 2 Rock burst grade and corresponding features

2.3 GA-ELM model

2.3.1 ELM basic principle

For N different samples (x_j, y_j), where x_j=[x_j1, x_j2, …, x_jn]^T∈Rⁿ, y_j=[y_j1, y_j2, …, y_jm]^T∈R^m, n and m are dimensions of input layer and output layer respectively. Then, a feedforward neural network with its excitation function G(x) and hidden layer nodes L can be represented by the following equation

                 (1)

where x∈Rⁿ, a_i∈Rⁿ, β_i∈R^m, i=1, …, L, j=1, …, N. a_i=[a_i1, a_i2, …, a_in]^T is the input weight connecting input layer with hidden layer nodes. b_i is the offset vector, the threshold of the i-th node. β_i=[β_i1, β_i2, …, β_im]^T is the output weight connecting hidden layer nodes with output layer. a_i·x_i represents the inner product of a_i and x_i. Excitation function G(x) can be RBF, sine or sigmoid.

Suppose that this feedforward neural network with L hidden layer nodes can be infinitely approximate to the N samples, namely

                        (2)

The following relationship exists among a_i, b_i and β_i,

              (3)

Equation (3) is simplified as

Hβ=Y                                      (4)

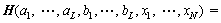
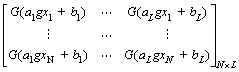   (5)

                         (6)

                         (7)

H is the hidden layer output matrix. For SLFNs, in general learning algorithms, the input weight a and offset vector b must be adjusted and constantly refreshed by iteration. In fact, for ELM algorithm, the values of a, b are not needed to be adjusted. What is to do is giving their values randomly at the beginning of the algorithm and accordingly calculating the output matrix H. So, the remaining work is to determine the parameter β. Training feedforward neural network can be transformed into a problem of seeking the least squares solution of the output weight matrix β. Output weight matrix β can be obtained by the following formula

                                    (8)

whererepresents the Moore-Penrose generalized inverse [10] of the hidden layer output matrix H. ELM algorithm procedure is as follows.

1) Set the input weight a_i and offset vector b_i randomly, where i=1, …, L, and L is the number of hidden layer nodes. 2) Select an infinitely differentiable function as the excitation function of hidden layer neurons and calculate the hidden layer output matrix H. 3) Calculate the output weight matrix β which connects hidden layer with output layer β= 4) When H and β are determined, the ELM model is obtained which may need a further verification with sample data. ELM network training model is shown in Fig. 7.

2.3.2 GA optimization process

Based on the algorithm characteristics of ELM model, the input weights a_i and offset vector b_i of the hidden layer are set at random. When the random value is set to 0, part of the hidden layer nodes will fail.

Fig. 7 ELM network training model

Prediction accuracy of ELM model is closely related to the number of nodes in the hidden layer. Only when the number of valid nodes is assured, can the accuracy of the model be guaranteed. However, excessive hidden layer nodes are bound to weaken the generalization performance of the model, reducing its prediction accuracy [11]. Taking into account the above-mentioned problems, GA is adopted to optimize the parameters of ELM model, including the number of hidden layer nodes L, hidden layer input weights a_i and offset vector b_i. To determine the optimal ELM model, training steps are as follows.

1) Determine the fitness function, population size k and evolutionary generations p. Fitness function is used to evaluate the pros and cons of the individuals. In the analysis, the mean square error of the model’s predictions for the validation set is selected as the fitness function. Obviously, the smaller the value of fitness function is, the more accurate the model is.

2) Randomly generate populations. Population size k is the number of individuals, which is generally set from 20 to 40. Individual dimensions D depend on the number of the model’s undetermined parameters, that is to say, input weight matrix and offset vectors of the hidden layer. Individual dimensions D and individual Q^γ can be represented as

D=L(n+1)                                   (9)

Q^γ=[a^γ₁₁, a^γ₁₂, …, a^γ_1L, a^γ₂₁, a^γ₂₂, …, a^γ_2L, …, a^γ_L1,

a^γ_L2, …, a^γ_LL, b^γ₁, b^γ₂, …, b^γ_L]              (10)

where L is the number of hidden layer nodes; n is the number of input layer neurons, the dimension of input vector. Q^γ is the γ-th individual, 1≤γ≤k; a_ij and b_j are randomly assigned on the interval [-1, 1].

3) Locally solve the optimal fitness function α^best. α^best is initialized to 10. θ and γ are initialized to 0. Then the sample data of training set is input into the model, solving the fitness function based on different individuals one by one until the end of the cycle when γ=k. In this way, the value of the α^best is gotten.

4) Globally solve the optimal fitness function α^best. After each round of step 3, evolve the populations based on crossover and mutation. Examine the value of evolutionary generations θ. When θ is not greater than p, the value of γ is initialized to 0 and it returns to the step 3. If θ is greater than p, end computing and the calculated α^best is the optimal fitness function value. The optimal ELM model can be determined based on the corresponding parameters.

The structural relationship of training steps is shown in Fig. 8.

Fig. 8 GA-ELM prediction model flowchart

2.4 Effect of structural surface on model

Rock mass is a kind of geological structure composed of rock and structural surface. Structural surface has a non-negligible impact on rock burst, which mainly depends on occurrence, spacing, continuity and other characteristics of structure surface. Essentially speaking, structural surface firstly affects the mechanical properties of rock mass, making it different from the intact rock, and thereby affects the occurrence of rock burst. This tends to lead a deviation between the data measured in laboratory and in engineering. However, these factors can not explain how the structural surface affects the model, because the model is established based on the mechanical properties of rock, which directly skipped the effect of structural surface in theory. Furthermore the training sample data of the model derive from engineering. So, how the structural surface affects the model needs a further discussion and validation.

Studies about the effect of structural surface on rock mass can be easily found. From the Yeager criterion [19], it is found that when rock damage occurs along the structural surface, the stresses in two-dimensional stress field must meet the conditions of shear strength, namely

                (11)

where σ₁ and σ₃ represent the primary stress; c₀ and φ₀ represent the adhesion and internal friction angle of the structural surface respectively; α is the angle between the structural surface and the first principal stress direction. In Yeager Criterion, when rock damage occurs along the structural surface, there exists an interaction between the primary stress σ₁, σ₃ and α, which can be expressed by the following expressions

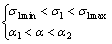                         (12)

(13)

where c and φ represent the adhesion and internal friction angle of intact rock respectively. So, Eq. (12) can be represented as Fig. 9.

Fig. 9 Rock damage discrimination curve

From the curve, it is found that for the determined primary stress σ₁, α is located within the interval [α₁:α₂]. The rock mass damage occurs along the structural surface, and the interval [α₁:α₂] is influenced by σ₁. When α is located outside the ranges of angle corresponding with the arc, rock mass will not be damaged along the structural surface. The level of σ_1max is influenced by σ₃, fluctuating up and down along the σ-axis. In short, the existence of structural surface reduces the maximum principal stress when rock is damaged.

Through numerical simulation and experimental tests [25-27], it is found that for rock with structural surface, its uniaxial compressive strength shows a tendency of firstly decreasing and then increasing along with the changes of α, which coincided with Yeager Criterion. In contrast, the uniaxial tensile strength continues decreasing. Furthermore due to the structural surface, uniaxial compressive strength decreased 2.36 times, while uniaxial tensile strength decreased 4.23 times, which indicates that the effect on uniaxial tensile strength is more obvious. In summary, the following conclusions can be obtained.

1) Uniaxial compressive strength and uniaxial tensile strength of the rock is reduced to varying degrees due to the structural surface, and the reduced magnitude of the former is smaller than that of the latter. 2) According to the single indicator criterion of rock burst, it can be learned that the stress indicator I becomes smaller, and the brittleness coefficient indicator K becomes larger, which tends to lead a brittle failure of rock. Combined with the rock complete stress-strain curve of the new model (Fig. 10) which is given by GE Xiurun academician [28], rock impact energy index W_CF becomes larger. 3) Structural surface will promote the occurrence of rock burst, which is not equivalent to the effect on the model. So, how it affects GA-ELM model still needs a further validation.

Fig. 10 Rock complete stress-strain curve of new model [28]

3 Engineering application

3.1 Sample selection

Taking Qinling Tunnel for example, Xi’an–Ankang Railway Qinling tunnel is about 18.46 km long. Rock around the tunnel is composed of mixed gneiss and mixed granite with characteristics of high strength and brittleness. Geological surveys and stress tests in construction phase show that the tunnel is located in high stress areas and the maximum principal stress direction is nearly SN [19, 20]. By monitoring and recording the rock burst in the construction process, sample data obtained are listed in detail in Table 3. Among them,1-20 samples are treated as training set, which is for training and optimization. 21-25 samples are treated as validation set, which is for validating the results of the optimized model and determining the optimal model’s parameters. 25-30 samples are treated as prediction set to predict the intensity of rock burst.

Table 3 Sample data

3.2 Model optimization

3.2.1 Hidden layer nodes optimization

With its input factors σ_θ, σ_c, σ_t and W_et as well as output factor t listed in Table 3, ELM prediction model is established. Sigmoid function is selected as the excitation function of ELM model. Firstly, the number of the hidden layer nodes is initialized to 20. Then, a_i and b_i are assigned randomly on the interval [-1,1]. Calculate the output weight matrix of ELM model, which is considered as a preliminary model. Use the validation set to verify the model and calculate the prediction accuracy rate. Follow the steps above, and gradually increase the number of hidden layer nodes in a cycle of 20. Then, compare the accuracy rate of predictions to determine the optimal number of hidden layer nodes. The results can be seen in Fig. 11.

Fig. 11 Accuracy rate of ELM model according to hidden layer nodes

As shown in Fig. 11, when the hidden layer nodes of ELM model do not exceed 150, the corresponding accuracy rate of predictions is rapidly rising. When it exceeds 450, the accuracy rate tends to maximum, no longer substantially continuing rising. Therefore, it can be determined that the number of the hidden layer nodes of the model L is 450.

3.2.2 Input weight a_i and offset vector b_i optimization

After the determination of L, GA is adopted to optimize a_i and b_i, further more determining the optimal ELM model. GA is realized based on Sheffield toolbox, encoding each individual in binary. Mean square error of the predictions which are calculated based on individuals and validation set is selected as the fitness function. Stochastic universal sampling is introduced in the selection operator and one-point crossover is introduced in the crossover operator. Other parameters of GA are as follows. Population size is k=40, the maximum evolutionary generations is p=100, crossover probability is 0.75, mutation probability is 0.02, and generation gap is 0.9.

The optimization process is illustrated in Fig. 8. The optimal fitness α^best=0.0197 and the corresponding values of a_i, b_i, which is the very parameters for the optimal GA-ELM model.

3.3 Result analysis

According to the optimized results, the prediction set is input into the model. The predicted results are shown in Table 4 and Fig. 12.

From Table 4 and Fig. 12, it is found that the predicted results of the GA-ELM model fit the measured results well, and that the relative error of predicted burst pit depths is small, which is controlled within 5%. Therefore, GA-ELM model has a high accuracy. Meanwhile, the model is established without considering the impact of structural surface, which directly shows that the impact of structural surface on GA-ELM model is little and negligible.

Table 4 GA-ELM model predictions and analysis

Fig. 12 Curves of predicted value and true value

4 Model comparisons

BP neural network model and SVM model are widely used in regression analysis, and have received good results to a certain extent. In order to demonstrate the superiority of the GA-ELM model, BP neural network model and SVM model are established and trained with the same sample data. The predicted results can be seen in Tables 5-6 and Fig. 13.

After the analysis of the data in Table 5 and Table 1, it is found that the prediction error of burst pit depth, ranging from 6.19% to 12.94%, shows bigger fluctuation with the BP neural network. The average relative error is up to 9.65%. It indicates that the stability of BP neural network model is relatively poor. There is no significant difference between SVM model and GA-ELM model in rock burst prediction. Compared with SVM model, GA-ELM model has a slightly higher stability with fewer parameter settings and neurons, which indicates a higher operational efficiency.

Table 5 BP neural network model and SVM model predictions

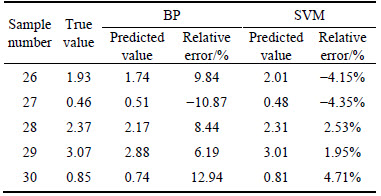
Table 6 Model accuracy analysis

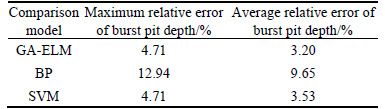
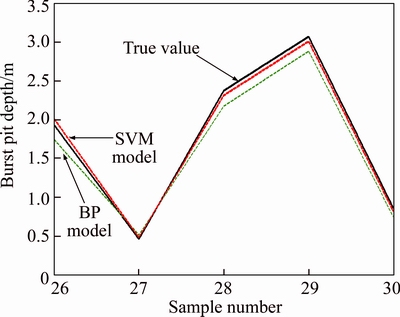
Fig. 13 Prediction curves of BP and SVM model

5 Conclusions

1) Through comparison of the factors affecting rock burst and the basic characteristics of it, the parameters of maximum shear stress, uniaxial compressive strength, uniaxial tensile strength and rock elastic energy index are selected as the input factors and burst pit depth as output factors, according to the mathematical model features. Thus the ELM prediction model of rock burst is proposed based on multi-index, which significantly improves the prediction accuracy of the model.

2) In order to avoid undermining the accuracy of the model due to random parameter selection, GA is introduced to optimize the model. After that the GA-ELM prediction model is obtained. Typical data is chosen for the model’s training and predicting. The prediction results show that the GA-ELM model has a high accuracy and the prediction error is controlled within 5%.

3) Predictions show that the effect of structural surface is very small. The reason is that the effect of structural surface on rock burst is indirect. It changes the mechanical properties of rock thereby affecting the rock burst. However, the model is based on the mechanical properties of rock and training samples are data measured in engineering, so the impact of structural surface has been taken into account when the model is trained with samples.

4) BP neural network model and SVM model are introduced to predict the intensity of rock burst. With the comparisons of the results from the three models, it is found that the prediction accuracy of GA-ELM model and SVM model is equivalent, which is higher than that of BP neural network model. That GA-ELM model can get the similar prediction accuracy with fewer parameter settings and neurons indicates its superiority to the latter.

References

[1] QIN C B, CHIAN S C, YANG X L. 3D limit analysis of progressive collapse in partly weathered Hoek–Brown rock banks [J]. International Journal of Geomechanics, 2017, 17(7), Article Number: 04017011. DOI: 10.1061/(ASCE)GM.1943-5622.0000885.

[2] YANG X L, LI W T. Reliability analysis of shallow tunnel with surface settlement [J]. Geomechanics and Engineering, 2017, 12(2): 313–326.

[3] YANG Xiao-li, LI Zheng-wei, LIU Zheng-an, XIAO Hai-bo. Collapse analysis of tunnel floor in karst area based on Hoek-Brown rock media [J]. Journal of Central South University, 2017, 24(4): 957–966.

[4] YANG X L, ZHANG R. Collapse analysis of shallow tunnel subjected to seepage in layered soils considering joined effects of settlement and dilation [J]. Geomechanics and Engineering, 2017, 13(2): 217–235.

[5] LI Z G, LI B, HAN X, SONG W P. Tunnel rockburst proneness study based on AHP-FUZZY method and field test [J]. Electronic Journal of Geotechnical Engineering, 2014, 19: 117-121.

[6] LI X W. Application of working face rock burst prediction of grey modeling cusp catastrophe analysis based on the acoustic emission [J]. Applied Mechanics and Materials, 2013, 373-375: 689-693.

[7] XIONG X B. Research on prediction of rating of rockburst based on BP neural network [J]. Open Civil Engineering Journal, 2014, 08(1): 463-469.

[8] SHI Y K, LI P R, WANG Y, ZHANG J Y. Classification and prediction of rock burst based on BP neural network [J]. Electronic Journal of Geotechnical Engineering, 2015, 20(18): 5839-5848.

[9] SHI X Z, ZHOU J, WU B B, HUANG D, WEI W. Support vector machines approach to mean particle size of rock fragmentation due to bench blasting prediction [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(2): 432-441.

[10] ZHOU J, LI X B, SHI X Z. Long-term prediction model of rockburst in underground openings using heuristic algorithms and support vector machines [J]. Safety Science, 2012, 50(04): 629-644.

[11] HUANG G, ZHU Q Y, SIEW C K. Extreme learning machine: theory and applications [J]. Neurocomputing, 2006, 70(1–3): 489-501.

[12] LAN Y, SOH Y, HUANG G B. Ensemble of online sequential extreme learning machine [J]. Neurocomputing, 2009, 72(13–15): 3391-3395.

[13] HUANG F, ZHAO L H, LING T H, YANG X L . Rock mass collapse mechanism of concealed karst cave beneath deep tunnel [J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 91: 133–138.

[14] YANG X L, LI K F. Roof collapse of shallow tunnel in layered Hoek-Brown rock media [J]. Geomechanics and Engineering, 2016, 11(6): 867–877.

[15] LI Y X, YANG X L. Stability analysis of crack slope considering nonlinearity and water pressure [J]. KSCE Journal of Civil Engineering, 2016, 20(6): 2289–2296.

[16] YANG Xiao-li, YAO Cong, ZHANG Jia-hua. Safe retaining pressures for pressurized tunnel face using nonlinear failure criterion and reliability theory [J]. Journal of Central South University, 2016, 23(3): 708–720.

[17] YANG X L, DU D C. Upper bound analysis for bearing capacity of nonhomogeneous and anisotropic clay foundation [J]. KSCE Journal of Civil Engineering, 2016, 20(7): 2702–2710.

[18] JIA Y P, LV Q, SHANG Y Q. Rock burst prediction using particle swarm optimization algorithm and general regression neural network [J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(2): 343-348. (in Chinese)

[19] MITSUO G, CHENG R W, YU X J. Genetic algorithms and engineering optimization [M]. Beijing: Tsinghua University Press, 2004: 24-30. (in Chinese)

[20] CAI M F, JI D, GUO Q F. Study of rock burst prediction based on in-site stress measurement and theory of energy accumulation caused by mining disturbance [J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 10: 1973-1980. (in Chinese)

[21] HE M C, MIAO J L, FENG J L. Rock burst process of limestone and its acoustic emission characteristics under true-triaxial unloading conditions [J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(2): 286-298.

[22] ZHOU H, MENG F Z, ZHANG C Q. Analysis of rockburst mechanisms induced by structural planes in deep tunnels [J]. Bulletin of Engineering Geology and the Environment, 2014, 74(4): 1435-1451.

[23] ZHANG W D, MA T H. Research on characteristic of rock burst and rules of micro seismic monitoring at diversion tunnels in Jinping II hydropower station [J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(2): 339-348. (in Chinese)

[24] YANG X L, YAO C. Axisymmetric failure mechanism of a deep cavity in layered soils subjected to pore pressure [J]. International Journal of Geomechanics, 2017, 17(8), Article Number: 04017031, DOI: 10.1061/(ASCE)GM.1943-5622.0000911.

[25] YANG X L, XU J S. Three-dimensional stability of two-stage slope in inhomogeneous soils [J]. International Journal of Geomechanics, 2017, 17(7), Article Number: 06016045, DOI: 10.1061/(ASCE)GM.1943- 5622.0000867.

[26] YANG X L. Effect of pore water pressure on 3D stability of rock slope [J]. International Journal of Geomechanics, 2017, DOI: 10.1061/ (ASCE)GM.1943-5622.0000969.

[27] YAN P, ZHAO Z G, LU W. Mitigation of rock burst events by blasting techniques during deep-tunnel excavation [J]. Engineering Geology, 2015, 188: 126-136.

[28] ZHAO Wen. Rock mechanics [M]. Changsha: Central South University Press, 2010: 20-21. (in Chinese).

(Edited by DENG Lü-xiang)

Cite this article as: LI Tian-zheng, LI Yong-xin, YANG Xiao-li. Rock burst prediction based on genetic algorithms and extreme learning machine [J]. Journal of Central South University, 2017, 24(9): 2105–2113. DOI: https://doi.org/ 10.1007/s11771-017-3619-1.

Foundation item: Project(2013CB036004) supported by the National Basic Research Program of China; Project (51378510) supported by the National Natural Science Foundation of China

Received date: 2016-02-22; Accepted date: 2016-07-11

Corresponding author: LI Tian-zheng, PhD, Tel: +86-13875988038; E-mail: jacksonic@126.com