基于核主元分析的滚动轴承故障混合域特征提取方法
彭涛1,杨慧斌2,李健宝2,姜海燕2,魏巍2
(1. 中南大学 信息科学与工程学院,湖南 长沙,410083;
2. 湖南工业大学 电气与信息工程学院,湖南 株洲,412008)
摘要:为有效利用时域、频域、时-频域中各类具有显著类别差异信息的非平稳统计特征,提高滚动轴承状态监测和故障诊断的性能和效率,提出一种基于核主元分析的混合域特征提取方法。通过对原始信号分别生成时域、频域状态特征,并利用多分辨率小波分解生成时-频域状态特征,构建出144个表征原始振动信号特征的混合域特征集。采用核主元分析方法对其中能敏感地反映故障特性的特征进行二次非线性特征提取,按累计贡献率大于90%的标准,选取前11个核主元作为主要特征量,将其输入支持向量机分类器进行状态识别。仿真结果表明:混合域特征集比单个特征、单域特征能更全面准确地反映故障特性,核主元分析方法能有效降低输入特征维数,并确保输出特征具有较高的反映轴承运行状态的敏感性和适于模式识别的可分性;与通常使用的基于小波分解的特征提取方法相比,本文方法能更加准确有效地提取不同运行条件下滚动轴承不同类型不同程度的故障特征。
关键词:混合域;特征提取;核主元分析;故障检测;轴承
中图分类号:TP277 文献标志码:A 文章编号:1672-7207(2011)11-3384-08
Mixed-domain feature extraction approach to rolling bearings faults based on kernel principle component analysis
PENG Tao1, YANG Hui-bin2, LI Jian-bao2, JIANG Hai-yan2, WEI Wei2
(1. School of Information Science and Engineering, Central South University, Changsha 410083, China;
2. College of Electrical and Information Engineering, Hunan University of Technology, Zhuzhou 412008, China)
Abstract: In order to effectively use the various nonstationary statistical features with significant differences from time domain, frequency domain and time-frequency domain, a novel mixed-domain feature extraction approach was proposed, which was based on kernel principle component analysis to improve the performance and efficiency for condition monitoring and fault diagnosis of rolling bearings. At first, the time-domain and frequency-domain features which were generated by the original signal, and time-frequency-domain features which were generated by the multi-resolution wavelet decomposition were extracted. The mixed-domain features set including 144 features were composed to characterize the original vibration signals. Then the kernel principle component analysis method was used to secondary extract the features which reflected sensitively the failure characteristics in the mixed-domain features set. According to the accumulated contribution rate of more than 90%, the first 11 nonlinear principal components were extracted as primary feature vector for support vector machine classifier to recognize. The results show that the mixed-domain features set can reflect the failure characteristics more comprehensively and accurately than a single feature or single-domain features. Kernel principle component analysis method can effectively reduce the input feature dimensions, and ensure the output features to be of high sensitivity to reflect the operational status of bearings and high separability or pattern recognition. Compared to the common feature extraction method based on wavelet decomposition, this proposed method becomes more apparent to extract fault feature of rolling bearing in different types and degrees under different operating conditions.
Key words: mixed-domain; feature extraction; kernel principal component analysis; fault detection; rolling bearings
轴承是机械系统中非常关键的部件,其性能直接影响到整个机械系统运行状况。尽管轴承运行过程是一个复杂的非平稳动态过程,很难用一个确定的时间函数来描述,但其振动信号仍具有特定的时域和频域特征,只是这些特征往往由于非平稳运行因素的影响被淹没在噪声中而难以提取。目前,利用非平稳信号处理方法获取的一些时域、频域和时-频域特征量已被有效应用于机械设备状态监测与故障诊断中[1-2]。不同的特征量包含的轴承运行状态信息各不相同,反映轴承运行状态规律性、敏感性和在模式空间的聚类性、可分性也不尽相同。由于单个或单域特征难以全面、准确地刻画出复杂机械系统在复杂工况下不同程度、不同类型的故障特性,文献[3]提出构建一种包括时域、频域、小波域的多域特征集合方法;文献[4-5]则从原始振动信号及其频谱、经传统滤波解调及经EMD分解的时序和包络谱共6个方面,提取表征设备运行状态的特征,构成多征兆域特征集,以获得较为全面、准确的故障特征信息。如何有效利用混合域中具有显著类别差异信息的特征,剔除对反映故障特性贡献不大、甚至不敏感的特征,并降低特征间的相关性、减少信息冗余,对高效、准确地诊断轴承故障至关重要。基于高斯统计假设的主元分析(Principal component analysis,PCA)作为常用的特征提取方法之一,对于非线性非平稳问题的处理结果往往较差。Scholkopf等提出的核主元分析(Kernel principal component analysis,KPCA)作为一种非线性分析方法,通过某种事先选择的非线性映射将原始数据映射到一个特征空间,然后对该空间中的映射数据进行线性主元分析,从而获得使原始数据具有更好可分性的非线性主元[6-7],该方法目前已在过程监控和故障诊断中得到越来越多的关注和成功的应用[8-10]。采用核主元分析方法对混合域特征集中对状态敏感的特征进行二次提取,将全部已有的特征映射到一个较低维的特征空间,用尽可能少的特征数最大程度地反映故障信息。在此,本文作者通过对原始信号分别生成时域、频域状态特征,并利用多分辨率小波分解的时间序列提取时-频域状态特征,构建表征原始振动信号状态特征的混合域特征集;然后,采用核主元分析方法从中提取对故障特性敏感的主要状态特征;最后,将提取出的非线性主元作为特征向量输入支持向量机进行状态识别,并应用于滚动轴承故障诊断实验,获得良好效果,验证了所提方法的有效性。
1 混合域特征集的构建
1.1 时域和频域特征生成
当轴承出现故障时,其振动信号在时域、频域的某些特征量会产生相应的变化。通过分析其变化可以有效识别出轴承运行状态。
根据滚动轴承运行振动信号的特点,分别在时域、频域生成可以较好地刻画状态变化特性的特征量,如表1所示,各特征量定义参见文献[1]。
表1 时域和频域生成的特征量
Table 1 Features of time-domain and frequency-domain

1.2 基于小波分解的时-频域特征提取
轴承故障的重要信息往往包含在瞬态信号或突变信号中,其对应的信号频率较高,而单一的时域或频域特征只能对信号进行整体刻画,不能同时对信号进行局域性分析。小波变换具有时-频域局部优化和可变时窗的特点,既可保持原始非平稳信号中的冲击与瞬态等高频信息,又可保留原始非平稳信号中的低频信息,用于分析非平稳信号比传统的时域、频域方法更具有显著的优点[11]。为此,采用Mallat算法[12]对轴承原始振动信号进行多分辨率分解,用不同频带内的分解系数生成一组新的时间序列;在这组新时间序列中采用原始振动信号的时、频域特征生成方法,构成时-频域特征向量,以便更加细致地刻画轴承在各频率波段中的状态变化。
对于任意信号 ,即
,即
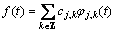 (1)
(1)
其中:系数 已知。采用Mallat算法在分辨率
已知。采用Mallat算法在分辨率 下,可将其分解为在
下,可将其分解为在 和
和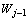 子空间的2个正交分量之和:
子空间的2个正交分量之和:
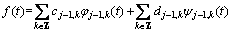 (2)
(2)
也就是由已知序列 可求出j-1级的近似序列
可求出j-1级的近似序列 和j-1级的细节序列
和j-1级的细节序列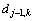 ,第j-1级信号的尺度系数和小波系数分别为:
,第j-1级信号的尺度系数和小波系数分别为:
 (3)
(3)
式中: 和
和 分别是L2(R)中某一正交多分辨率分析的尺度函数和小波母函数,R为实数集,且有:
分别是L2(R)中某一正交多分辨率分析的尺度函数和小波母函数,R为实数集,且有:
 (4)
(4)
 (5)
(5)
{hk}和{gk}分别为分解用低通、高通滤波器系数,可以通过内积来计算:
 (6)
(6)
如果对信号进行多级小波分解,即从j=0级开始经过J级分解,最后得到的是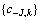 ,
, ,…,
,…, ,
, ,共J+1个序列:
,共J+1个序列:
 (7)
(7)
 ,j=1, 2, …, J (8)
,j=1, 2, …, J (8)
其中:CJ是信号f(t)的第J级近似序列;Dj是信号f(t)的第j级细节序列。通常,将原始采样数据{fn}看作是f(t)在j=0级的近似序列{c0, k}。
对轴承原始振动信号进行6层小波分解,可以生成7个新的时间序列,对这7个时间序列分别生成如表1所示的14个时域特征量和4个频域特征量,共生成126个时域和频域特征量。
为从多个不同角度准确刻画轴承故障特性,全面反映轴承运行状态,将生成的14个时域特征、4个频域特征和126个时域和频域特征构成具有144个时域、频域和时域和频域特征量的混合域特征集。
2 基于核函数主元分析的特征提取
混合域特征集中每个特征量对不同运行条件下不同类型不同程度故障的敏感性不同;不同特征所包含状态信息之间的相关性及同一域中不同特征之间的相关性也不尽相同,一些特征甚至会互相削弱反映故障特性的能力。因此,采用核主元分析方法对混合域特征集中状态敏感的特征进行二次提取,以降低相关性、减少冗余,获取数目少、敏感性高且分类错误率小的主要特征向量。
基于核主元分析的特征提取方法如图1所示,具体步骤如下。
(1) 构建混合域特征集。用前面介绍方法,对待分析信号进行第1次特征提取,构建混合域特征集。
(2) 进行非线性映射。用非线性映射Φ将混合域特征空间R中的原始数据xi(i=1, …, M)映射到新的特征空间F的像 中。
中。
定义映射数据的M阶对称方阵K的元素Kij为核函数:
 ;i=1, …, M;j=1, …, M (9)
;i=1, …, M;j=1, …, M (9)
本文选择Kij为径向基核函数:
 (10)
(10)
式中: 为标准差,一般采用逐点试选法获得。
为标准差,一般采用逐点试选法获得。
若映射数据为非零均值,则需对核函数进行中 心化:
 (11)
(11)
式中:1M是元素为1/M的M×M阶常数方阵, 和
和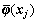 为中心化后的映射数据。
为中心化后的映射数据。
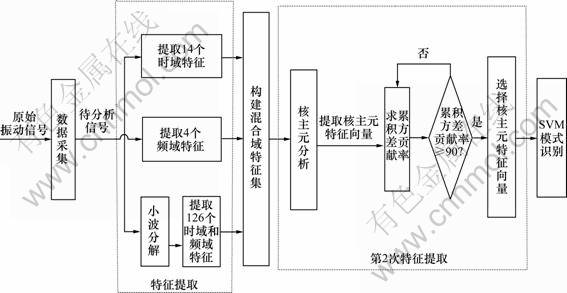
图1 基于核主元分析的特征提取方法示意图
Fig.1 Graph of feature extraction approach based on kernel principle component analysis
(3) 提取核主元特征量。对映射后的数据进行线性主元分析,获得使原始数据具有更好可分性的非线性主元[6-7]。
设 的协方差矩阵
的协方差矩阵 的特征值为λ,相应的特征向量为v,则有:
的特征值为λ,相应的特征向量为v,则有:
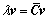 (12)
(12)
其中:
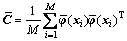 (13)
(13)
对于所有的l=1, …, M,将映射数据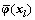 分别与式(12)两边做内积,有:
分别与式(12)两边做内积,有:
 (14)
(14)
并且存在系数 (j=1, …, M),使
(j=1, …, M),使
 (15)
(15)
成立。于是,
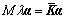 (16)
(16)
式中:α为对应于矩阵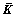 特征值Mλ的特征向量。
特征值Mλ的特征向量。
将矩阵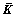 对角化后的特征值记为
对角化后的特征值记为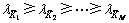 ,设
,设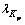 为其中大于0的特征值的最小值,于是,映射后的数据在特征向量vk(k=1, …, p)上的投影,即为通过非线性映射Φ所求得的原始数据xi的非线性主元:
为其中大于0的特征值的最小值,于是,映射后的数据在特征向量vk(k=1, …, p)上的投影,即为通过非线性映射Φ所求得的原始数据xi的非线性主元:
 (17)
(17)
式中: 为对应于矩阵
为对应于矩阵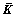 对角化后特征值的特征向量
对角化后特征值的特征向量 的第j个元素,且
的第j个元素,且 ,k=1, …, p。
,k=1, …, p。
(4) 求累积方差贡献率。累积方差贡献率RCVC定义为:
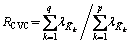 (18)
(18)
式中:q≤p。
(5) 选择核主元特征量。以RCVC≥90%为标准,
从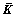 的特征值
的特征值 中,由大到小选取前q个特征向量作为核主元特征量。
中,由大到小选取前q个特征向量作为核主元特征量。
3 仿真分析
将基于核主元分析的混合域特征提取方法应用于滚动轴承故障诊断实验中。实验数据全部来自美国Case Western Reserve 大学轴承实验中心,测试轴承为6205-2RS深沟球轴承,实验装置和轴承尺寸见文献[13]。信号采样频率为48 kHz。
通过加速度传感器获取滚动轴承在正常、内环故障、外环故障及滚动体故障等情况下运行时的原始振动信号,对应故障点直径分别为0.533 4,0.355 6和0.177 8 mm,负载依次为0,0.735和1.47 kW,转速依次为1 797,1 772和1 750 r/min等运行条件,共获得对应12种运行状态下原始振动信号的12个采样数据集。设第i种状态采样数据集的采样点数为ni(i=1, 2, …, 12),以1 024个采样点为1个样本,则各采样
数据集包含的样本数为 。从每种运行状态
。从每种运行状态
中随机选取30个样本用于训练,余下的样本用于测试,如表2所示。图2给出了状态1~4的原始振动信号时域波形。可见:仅从时域波形图是难以区别不同运行状态及其特征的。
采用支持向量机分类器[14-15]对所提取的特征进行状态识别,以 (其中:
(其中: 为分类准确率;N0为正确识别的样本数)验证本文方法的有效性。基于支持向量机的故障识别步骤如下。
为分类准确率;N0为正确识别的样本数)验证本文方法的有效性。基于支持向量机的故障识别步骤如下。
(1) 用前面介绍的基于核主元分析的特征提取方法,对训练样本进行2次特征提取。
表2 轴承测试的12种运行状态
Fig.2 12 running states of bearing test

图2 滚动轴承原始振动信号时域波形
Fig.2 Wave forms in time domain of vibration signal of rolling bearings
进行第1次特征提取时,考虑振动信号采样频率为48 kHz,轴承内环、滚动体、外环3种类型故障频率范围为几十至几百Hz,且需基本覆盖轴承损伤所引起的共振频带要求,对分析信号进行6层DB10小波分解,获得7个频带即[0, 375],[375, 750],[750, 1 500],[1 500, 3 000],[3 000, 6 000],[6 000, 12 000]和[12 000, 24 000] Hz的时间序列。
进行第2次特征提取时,根据经验预选径向基核函数的标准差参数σ初始值为0.01,步长为5,终值为100,进行逐点实验,获取如图3所示标准差参数与某类样本(分别对应故障点直径为0.533 4,0.355 6和0.177 8 mm)整体分类准确率的关系曲线。取整体识别率最大值所对应的核函数标准差参数作为该类训练样本的最优标准差参数,建立该类训练样本的KPCA模型,按照累计贡献率大于90%的标准,选出前11个核主元作为该类训练样本的特征量。

图3 标准差参数与某类样本整体分类准确率的关系曲线
Fig.3 Relationship between standard deviation parameter and whole classification accurate rate of sample
(2) 用训练样本的11个核主元特征量训练支持向量机分类器。使用二分类支持向量机构造多类SVM分类器,每2类训练1个分类器。对于1个k类分类器问题,需要有k(k-1)个二分类器,具体方法可参见文献[14]。
(3) 据步骤(1)建立测试样本的KPCA模型,并提取测试样本的11个核主元特征量。
(4) 将测试样本的核主元特征量输入到经步骤(2)训练好的SVM分类器中,进行故障识别与分类。
为验证本文方法的有效性,进行了5个实验。
实验Ⅰ:将混合域中共144个特征逐个输入SVM进行状态识别。采用基于距离评价技术的特征选择方法[3-4]从14个时域特征、4个频域特征以及126个 时-频域特征中,仅分别选出2个、1个和 2个对故障最为敏感的特征的识别结果,依次标记为A1,A2,B1,C1和C2。
实验Ⅱ:将混合域中的单域特征,即时域特征(14个向量)、频域特征(4个向量)、以及时-频域特征(126个向量),分别输入SVM进行状态识别,结果依次标记为A,B和C。
实验Ⅲ:将混合域特征集中的144个特征直接输入SVM进行状态识别,结果标记为D。
实验Ⅳ: 对混合域中的单域特征,即时域特征(14个向量)、频域特征(4个向量)以及时-频域特征(126个向量),分别采用基于KPCA特征提取方法,提取核主元特征向量5,3和11个,输入SVM进行状态识别,结果依次标记为Ak,Bk和Ck。
实验Ⅴ:对混合域特征集的144个特征进行KPCA特征提取,提取核主元特征向量11个,输入SVM进行状态识别,结果标记为Dk。
实验Ⅰ的识别结果见表3,实验Ⅱ和Ⅲ的识别结果见表4,实验Ⅳ和Ⅴ的识别结果见表5。
为进一步验证本文所提方法的有效性,进行了对比实验Ⅵ:对原始振动信号进行6层DB10小波分解,得到7个归一化的频带能量特征,将其直接输入SVM进行状态识别,结果标记为E,见表5。
表3 实验Ⅰ分类准确率
Fig.3 Classification identification accuracy rates of testⅠ %
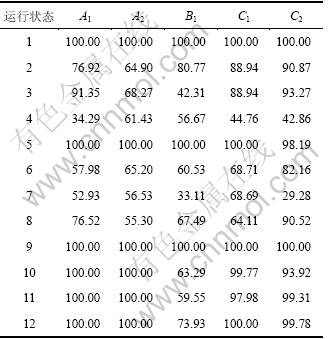
表4 实验Ⅱ和Ⅲ分类准确率
Fig.4 Classification identification accuracy rates of test Ⅱ and Ⅲ %

表5 实验Ⅳ和Ⅴ分类准确率
Fig.5 Classification identification accuracy rates of test Ⅳ and Ⅴ %

对比表3~5可以看出:在相同条件下,使用相同的分类器,采用本文所提出的基于核主元分析混合域特征提取方法,所获得的分类准确率(Dk)均超过了97%,这说明:混合域特征集比单个特征、单域特征能更全面准确地反映故障特性;核主元分析方法能有效降低输入特征维数,并确保输出特征具有较高反映轴承运行状态的敏感性和适于模式识别的可分性;基于核主元分析的混合域特征提取方法对滚动轴承在不同工况、不同类型、不同程度故障特征的提取效果更为良好。
4 结论
(1) 利用非平稳信号处理方法,分别从时域、频域和时-频域获取各种类别特征量,构建了一种混合域特征集,可以获得较全面、准确的滚动轴承不同工况不同类型不同程度故障的特征信息。
(2) 利用核主元分析方法对混合域特征集进行特征2次提取,可以将全部已有的特征映射到1个较低维的特征空间,有效剔除那些对反映故障特性贡献不大甚至不敏感的特征,并提取出对状态敏感的特征,从而获得数目少、敏感度高且分类错误率小的主要特征量。
(3) 本文提出的方法可以准确、有效地提取滚动轴承在不同运行状况、不同类型、不同程度的故障 特征。
参考文献:
[1] 温熙森. 模式识别与状态监控[M]. 北京: 科学出版社, 2007: 147-165.
WEN Xi-sen. Pattern recognition and condition monitoring[M]. Beijing: Science Press, 2007: 147-165.
[2] Samantha B, Balushi K R A. Artificial neural network based fault diagnostic of rolling element bearing using time domain features[J]. Mechanical Systems and Signal Processing, 2003, 17(2): 317-328.
[3] Arnaz M, Robert X G. PCA-based feature selection scheme for machine defect classification[J]. IEEE Transactions on Instrumentation and Measurement, 2004, 53(6): 1517-1525.
[4] 雷亚国, 何正嘉, 訾艳阳. 基于混合智能新模型的故障诊断[J]. 机械工程学报, 2008, 44(7): 112-117.
LEI Ya-guo, HE Zheng-jia, ZI Yan-yang. Fault diagnosis based on novel hybrid intelligent model[J]. Chinese Journal of Mechanical Engineering, 2008, 44(7): 112-117.
[5] LEI Ya-guo, HE Zheng-jia, ZI Yan-yang. Application of an intelligent classification method to mechanical fault diagnosis[J]. Expert Systems with Applications, 2009, 36(6): 9941-9948.
[6] Scholkopf B, Smola A, Muller K R. Nonlinear component analysis as a kernel eigenvalue problem[J]. Neural Computation, 1998, 10(5): 1299-1319.
[7] Scholkopf B, Smola A, Muller K R. Kernel principal component analysis[C]//Advances in Kernel Methods-support Vector Learning. Cambridge: MIT Press, 1999: 327-352.
[8] Lee J M, Yoo C K, Choi S W, et al. Nonlinear process monitoring using kernel principal component analysis[J]. Chemical Engineering Science, 2004, 59(1): 223-234.
[9] 蒋少华, 桂卫华, 阳春华, 等. 基于核主元分析与支持向量机的监控诊断方法及其应用[J]. 中南大学学报: 自然科学版, 2009, 40(5): 1323-1328.
JIANG Shao-hua, GUI Wei-hua, YANG Chun-hua, et al. Method based on kernel principal component analysis and support vector machine and its application[J]. Journal of Central South University: Science and Technology, 2009, 40(5): 1323-1328.
[10] 胡金海, 谢寿生, 侯胜利, 等. 核函数主元分析及其在故障特征提取中的应用[J]. 振动、测试与诊断, 2007, 27(1): 48-52.
HU Jin-hai, XIE Shou-sheng, HOU Sheng-li, et al. Kernel principal component analysis and its application to fault Feature extraction[J]. Journal of Vibration, Measurement & Diagnosis, 2007, 27(1): 48-52.
[11] Rubini R, Meneghetti U. Application of the envelope and wavelet transform analyses for the diagnosis of incipient faults in ball bearings[J]. Mechanical Systems and Signal Processing, 2001, 15(2): 287-302.
[12] Mallat S G. A theory for multiresolution signal decomposition: The wavelet representation[J]. IEEE Transactions on Patten Analysis and Machine Intelligence, 1989, 11(7): 674-373.
[13] Case Western Reserve University. Case Western Reserve University Bearing Data Center[EB/OL]. http://www. eecs.cwru.edu/laboratory/bearing/. 2011.
[14] 何学文, 赵海鸣. 支持向量机及其在机械故障诊断中的应用[J]. 中南大学学报: 自然科学版, 2005, 36(1): 97-101.
HE Xue-wen, ZHAO Hai-ming. Support vector machine and its application to machinery fault diagnosis[J]. Journal of Central South University: Science and Technology, 2005, 36(1): 97-101.
[15] 杨正友, 彭涛. 基于振动信号分析和支持向量机的滚动轴承故障诊断[J]. 湖南工业大学学报,2009, 23(1): 96-99.
YANG Zheng-you, PENG Tao. Fault diagnosis of rolling element bearing based on vibration signal analysis and support vector machine[J]. Journal of Hunan University of Technology, 2009, 23(1): 96-99.
(编辑 陈灿华)
收稿日期:2010-11-08;修回日期:2011-02-25
基金项目:国家自然科学基金资助项目(60774069);省部级重点基金资助项目(9140A17051010BQ0104);中国博士后科学基金资助项目(20070410462);湖南省教育厅科技计划项目(07C005)
通信作者:彭涛(1965-),女,湖南汉寿人,博士,教授,从事复杂过程、设备故障诊断等研究;电话:0731-88876677;E-mail: pandtao@yahoo.com.cn