Trans. Nonferrous Met. Soc. China 27(2017) 686-693

Recovery prediction of copper oxide ore column leaching by hybrid neural genetic algorithm

Fatemeh Sadat HOSEINIAN¹, Aliakbar ABDOLLAHZADE^1,2, Saeed Soltani MOHAMADI², Mohsen HASHEMZADEH³

1. Department of Mining & Metallurgical Engineering, Amirkabir University of Technology, Tehran, Iran;

2. Department of Mining Engineering, University of Kashan, Kashan, Iran;

3. Department of Chemical and Materials Engineering, University of Alberta Edmonton, Alberta T6E 2H8, Canada

Received 4 March 2016; accepted 7 September 2016

Abstract: The artificial neural network (ANN) and hybrid of artificial neural network and genetic algorithm (GANN) were applied to predict the optimized conditions of column leaching of copper oxide ore with relations of input and output data. The leaching experiments were performed in three columns with the heights of 2, 4 and 6 m and in particle size of <25.4 and <50.8 mm. The effects of different operating parameters such as column height, particle size, acid flow rate and leaching time were studied to optimize the conditions to achieve the maximum recovery of copper using column leaching in pilot scale. It was found that the recovery increased with increasing the acid flow rate and leaching time and decreasing particle size and column height. The efficiency of GANN and ANN algorithms was compared with each other. The results showed that GANN is more efficient than ANN in predicting copper recovery. The proposed model can be used to predict the Cu recovery with a reasonable error.

Key words: leaching; copper oxide ore; recovery; artificial neural network; genetic algorithm

1 Introduction

Heap leaching is a hydrometallurgical method that is used to leach low grade minerals such as copper, gold, nickel and zinc. In this method, piles of crushed ore are irrigated with various chemical solutions to leach and extract valuable minerals [1]. The effects of metallurgical parameters (such as particle size, porosity and permeability of ore, temperature, column height, solvent concentration, leaching time, solution flow rate, and mineralogy and chemistry of ore) on the process are usually studied using column leaching test. The results of column leaching are used in the optimization, planning, control and design of heap leaching [1-8].

Many experimental and modeling studies such as analytical and mathematical modeling have been carried out to gain a better understanding of the heap leaching process and its operation [9,10]. However, little research has been conducted with the aim of optimizing the process. Recently, analytical models have been used for planning, optimization, design and control of the heap leaching process and a mathematical model for heap leaching has been presented that was useful for designing and scaling up the processes [11]. MELLADO et al [7,12] also used an analytical model to optimize the flow rates on copper heap leaching. In this regard, they carried out an analytical–numerical method to solve a heap leaching problem of one or more solid reactants from porous pellets. VEGLIO et al [13] evaluated the effect of some main parameters on the column leaching of a manganese dioxide ore using fractional factorial design. CHELGANI and JORJANI [14] used the artificial neural network for the prediction of Al₂O₃ leaching recovery in the Bayer process. They studied the relationship between the recoveries of leaching and the chemical modules of bauxite fed to the process using methods of ANN and regression. They noted that the proposed ANN could be used for the prediction of Al₂O₃ leaching recovery.

The objective of this study is to obtain optimum conditions for column leaching by testing main parameters involved in the leaching process. Artificial neural network (ANN) model is developed to predict the recovery of column leaching, by taking into account four leaching parameters as inputs to the model, such as column height, particle size, acid flow rate and leaching time. In order to improve prediction accuracy, the genetic algorithm (GA) is incorporated in the training phase of a network, involving two objectives: the mean squared error (MSE) and determination coefficient (R). The process data are used for the recovery prediction of Cu column leaching using ANN and hybrid of ANN and GA.

2 Materials and methods

2.1 Data sets

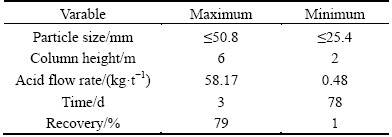
Tests were performed on copper oxide ore obtained from Tarom deposit, Zanjan, Iran. Sulfuric acid with concentration of 20 g/L was used for ore leaching, and LIX98N solvent was used for extraction of copper from leach liquor.

The initial sample ore was split into two samples. One was crushed to less than 50.8 mm by a jaw crusher and the other to less than 25.4 mm. After blending, representative samples were collected for particle size distribution analysis, chemical analysis, and mineralogical characterization. Screen analysis was performed by mechanically shaken Tyler sieves.

Chemical analysis of elements was carried out by ICP-emission spectrophotometry. The X-ray diffraction (XRD) analysis of ore was used in order to determine the mineralogical species. The crushed samples were agglomerated with 30% of their maximum sulfuric acid consumption (30 kg/t) and then charged within the columns.

Sulfuric acid solutions were freshly prepared as needed, every three or four days. Leaching solutions were fed by peristaltic pumps. Every other day of leaching, a given amount of pregnant leach solution (PLS) sample was taken and quantitatively analyzed for copper and free sulfuric acid. Copper was extracted from PLS by the solvent extraction method using LIX984N and the raffinate solutions were circulated after adjusting its acid concentration. The leaching experiments were stopped when the copper concentration of PLS reached 0.1%. The experiments with 2, 4 and 6 m columns were completed within 78 d.

2.2 Effect of parameters

The results showed that the copper recovery has an inverse relation with the column height and particle size, and a direct relation with the leaching time and the acid flow rate. The obtained copper recoveries in the columns with the heights of 2, 4 and 6 m and particle size of 25.4 and 50.8 mm during column leaching over 78 d are shown in Table 1. One of the important factors in the leaching of copper from ore is time. Copper in the ore undergoes physical and chemical reactions. Figure 1 shows that the copper recovery increases with increasing the leaching time (has a polynomial relation) and decreasing the particle size. Figure 2 shows that the copper recovery increases with increasing the time and acid flow rate. More fresh solution is irrigated over the column with increasing the leaching time, which causes the dissolution of more minerals and increasing the copper recovery. Figure 3 shows that the copper recovery decreases with increasing the column height and particle size. Finer particles provide more available mineral surface to contact with acid solution so that more copper can be leached. The recovery increases with decreasing the height of column. Therefore, in order to maintain the same acid flow rate and the same recovery, it is necessary to increase the surface area of column, and a larger volume of acid is required.

Table 1 Effect of column height and particle size on copper recovery

Fig. 1 Effect of time and particle size on recovery of copper during column leading

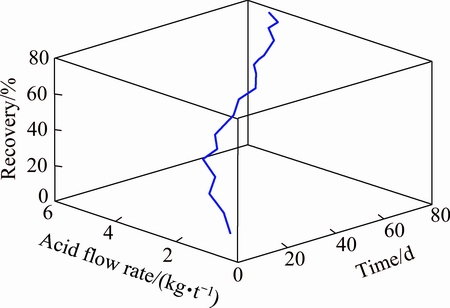
Fig. 2 Effect of time and acid flow rate on recovery of copper (ore crushed to less than 25.4 mm with heap height of 2 m)

Fig. 3 Comparison between copper recovery in 25.4 mm and 50.8 mm crushed ores

2.3 GANN model

Artificial neural networks (ANN) have been used in the mineral processing. They are used successfully in some research and industrial work. They are capable of modeling and controlling complicated systems and identifying very difficult relations between input and output data [15]. Neural networks are utilized to establish a relationship between a set of inputs and outputs. ANN uses a set of nonlinear basis functions between input and output data to be communicated, which acts as a black box [16]. In general, a neural network consists of one input layer, one or more hidden layers and one output layer. Each layer consists of one or more neurons [14]. The neurons are inter-related by using a weight parameter. Each neuron in a layer receives information from all neurons of the previous layer. According to the characteristics of the data input/output, the amount of bias and their inner connections are added with other neurons and transferred to the next layer [17,18].

One of the most useful types of neural networks is the back-propagation algorithm (BP). BP is used to converge the minimum error [16]. In this network, the error is calculated and then, according to the error rate, the weights communication and bias are updated [19]. The background of data processing details is described by SINGH et al as follows.

In an ANN, the jth neuron in the hidden layer is connected to a number of inputs:

x_i=(x₁, x₂, x₃, …, x_n)                           (1)

The net input values in the hidden layer will be

Net_j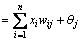                            (2)

where x_i is the input units, θ_j is the bias neuron (optional), w_ij is the weights on the connection of the ith input and jth neuron, and n is the number of input units. The net output of hidden layer in this study is calculated using a logarithmic sigmoid function.

                (3)

The total input to the kth unit is

O_k=f(Net_k)                                   (4)

The network is presented with input and output patterns in the learning process. The network output is computed by the network. Now, the actual output and the desired output are compared with each other. Therefore, error at any output in layer k is

e_l=t_k-O_k      (5)

where t_k is the desired output and O_k is the actual output. The total error function is

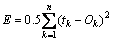                          (6)

Training is done for achieving an optimum weight space of the network. The steepest descent error surface is given by the following rule:

                        (7)

where η is the learning rate parameter and E is the error function. Updated weights for the (n+1)th pattern are given as

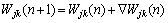                  (8)

The hidden and output layers are connected with the similar logic [16,17]. Optimization of design and structure of ANN and weights and bias of network can be done by the genetic algorithm.

Genetic algorithm (GA) is a stochastic general search method that can solve a wide variety of optimization problems by principles of Darwinian natural selection [20]. Each possible response of issue can be presented as a chromosomes in the algorithm. A population is constructed from the collection of chromosomes [21]. An objective function is defined according to main aim to evaluate the fitness values of all the chromosomes. In this method, a random population was generated that was tested with a given fitness function. At each iteration, selecting a particular group of parents to generate offspring using mutation and crossover from the former ones and then evaluating the fitness of all the new offsprings are repeated. The process of GA algorithm is continued to reach the determined conditions [21]. The response of the best process simulated evolution can become a good solution to the problem. GA has been successfully used in mineral processing in order to circuit design, optimization of parameters and process control process control [22-24].

GA can be used for the optimization of weights of a BP neural network, learning parameters and finding the network structure. This work only used GA for the optimization of weights of a BP neural network [21,25-27]. The total number of connection of the ANN is determined as the length of the  chromosome [25,28]. The flow chart of the algorithm is shown in Fig. 4.

GA has been used for the optimization of weights and the threshold of neural network of BP algorithm. We used the GA population size of 150, and the top scoring 15% of the population was selected as fit to survive in the next generation of solutions. We used 50% and 35% of the population for the crossover and mutation, respectively. The maximum generation selected equaled 200. The arithmetic crossover was used to produce two new offsprings by a linear combination of two parents. Two parents 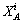 and  were selected that crossed each other; then the new offsprings ( and 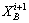) are produced:

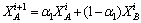                      (9)

                    (10)

where α₁ and α₂ are the random numbers in the range of 1 and the number of elements in array of.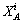

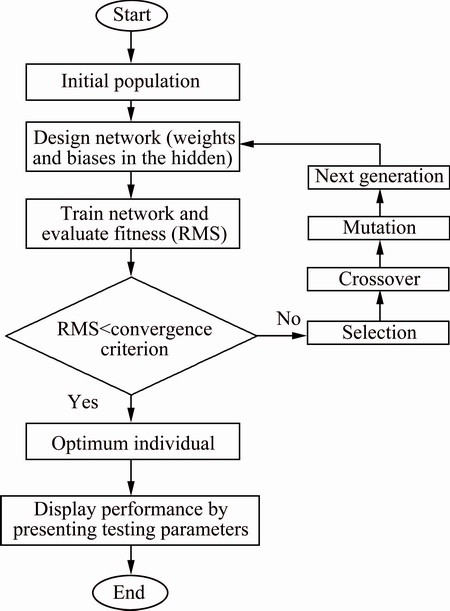
Fig. 4 Flow chart of using GA to optimize BP algorithm

Mutation point (x_k) is in the range of . The genetic value of mutation point is

                    (11)

where r is a random number in the range of the number of selected parents for mutation and the number of total parents [27].

The connection weights of the new population offspring given to neural network and the fitness function of the new offspring were calculated. The process of genetic operations continued until it reached the predetermined value [28].

3 Parameter selection and modeling using ANN and GANN

In this study, ANN and GANN were used. To train the networks, 120 sets of data recorded in the column leaching of Tarom copper ore were used, in which 96 sets were used to train the network and 24 sets to test its correctness. All input and output data (before feeding to the networks) were normalized in the range of 1 and -1. The particle size, column height, leaching time and acid flow rates are input parameters of the network. Table 2 presents the statistical parameters for the networks. The designed network output is copper recovery. Figure 5 shows the network back propagation algorithm.

Table 2 Statistical parameters of networks

4 Result and discussion

The back propagation algorithm was used for training the network, which does not always converge to the absolute minimum and has a weak rate of convergence. The connection weights of ANN by BP algorithm are only adjusted from the local angle and the whole learning process form the global perspective is not examined. Therefore, it may be stopped in a local minimum [28]. The combined BP and GA have been used for the better training of the neural network works. GA is also used to optimize the BP algorithm to overcome BP disadvantage of being easily stopped in a local minimum. It uses to learn the connection weights and bias of ANN.

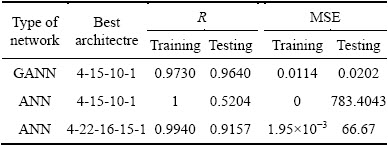
The optimal topology of the networks designed for column leaching processes with 3 and 4 hidden layers and one output layer for ANN and GANN in the form {4-15-10-1} and ANN in the form {4-22-16-15-1} is shown in Figs. 6 and 7, respectively. The numbers of layers and neurons in each layer are limiting elements in training so that the training time increases with increasing them. The numbers of hidden layers and neurons in GANN network are less than those in ANN in the form {4-22-16-15-1}.

Figure 8 shows the total squared error and comparison of the response of GANN in the training process. The figure shows that the sum squared error reduces with the increase of generation and the measured Cu recoveries are close to the estimated recoveries by GANN in the training process.

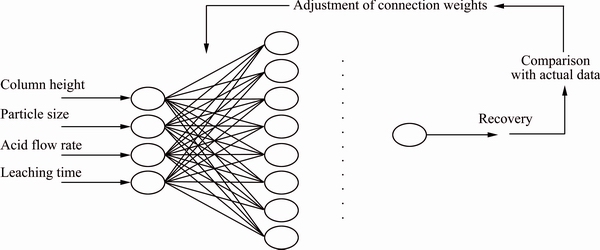
Fig. 5 Network back propagation algorithm for prediction of heap leaching recovery

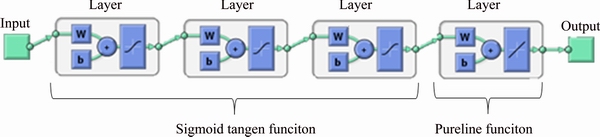
Fig. 6 GANN and ANN structure for prediction of heap leaching recovery in form {4-15-10-1}

Fig. 7 ANN structure for prediction of heap leaching recovery in form {4-22-16-15-1}

For the validation of the GANN and ANN models, the test data were used in the trained model. Figure 9 shows the measured values of Cu recovery in comparison with the predictions of GANN for each sample. The assessment of the correlation coefficients (R) of training and testing phases using GANN and ANN algorithm in the form {4-15-10-1} and ANN algorithm in the form {4-22-16-15-1} are shown in Figs. 10-15, respectively. As shown in these figures, the recovery values measured in the laboratory and predicted by the GANN and ANN algorithm in the form {4-22-16-15-1} are close to each other in the training and testing of networks. The gradient of the regression line between the measured Cu recoveries with the estimated by GANN and ANN in the form {4-15-10-1} and ANN in the form {4-22-16-15-1} in the training and testing are equal to 0.97, 1, 0.96 and 0.99, 0.5204, 0.92, respectively, in which the values of R in the GANN and ANN in the form {4-22-16-15-1} are close to its optimal value (1). The efficiency of ANN is increased with increasing the number of hidden layers and neurons. The mean squared error (MSE) and determination coefficient (R) of these networks are presented in Table 3. The testing MSE for GANN is less than the ANN ones. Therefore, the efficiency of GANN is more than that of ANN for the prediction of the Cu recovery in column leaching.

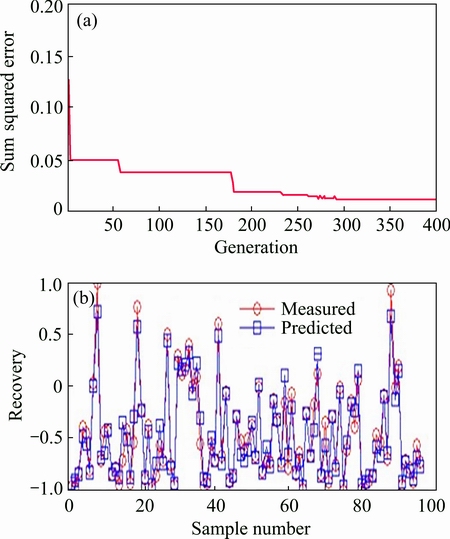
Fig. 8 Sum squared error during generation of GANN (a), and comparison of measured Cu recovery with that estimated by GANN in training process (b)

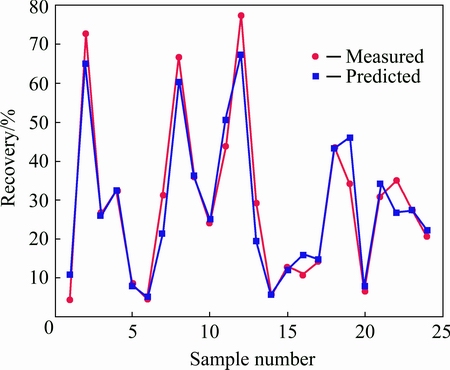
Fig. 9 Comparison of measured Cu recovery with that estimated by GANN in testing process

Fig. 10 Predicted Cu recovery by GANN in training process vs actual measurement

Fig. 11 Predicted Cu recovery by GANN in testing process vs actual measurement

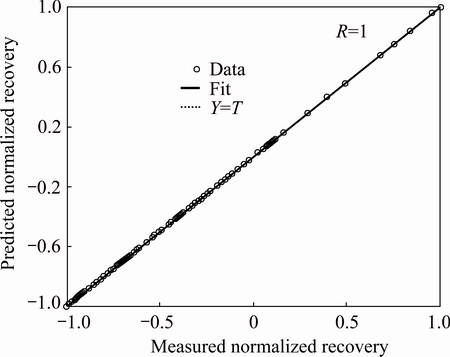
Fig. 12 Predicted Cu recovery by ANN in training process vs actual measurement in form {4-15-10-1}

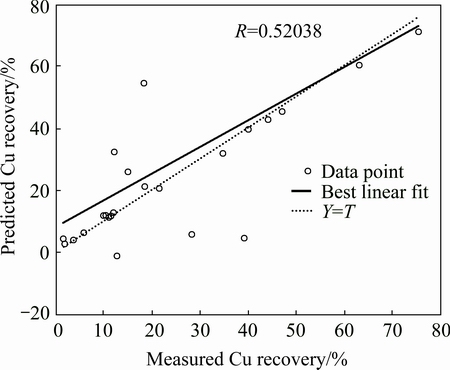
Fig. 13 Predicted Cu recovery by ANN in testing process vs actual measurement in form {4-15-10-1}

Fig. 14 Predicted Cu recovery by ANN in training process vs actual measurement in form {4-22-16-15-1}

Fig. 15 Predicted Cu recovery by ANN in testing process vs actual measurement in form {4-22-16-15-1}

Table 3 Statistical measures and performance of ANN and GANN models for training and testing

5 Conclusions

In this study, parameters such as column height, particle size, acid flow rate and leaching time in pilot scale were optimized. GANN as a novel procedure was used for recovery prediction in the column leaching. ANN and GANN were trained for the recovery of column leaching with the input parameters such as: particle size, column height, acid flow rate and leaching time. Three columns with the heights of 2, 4 and 6 m and in particle size of <25.4 and <50.8 mm were used to evaluate the effect of column height and particle size. The result showed that the recovery increased with increasing the acid flow rate and leaching time and decreasing particle size and column height. In these networks, multi-layer ANN back propagation and GANN algorithm with {4-22-16-15-1} and {4-15-10-1} arrangement were used to the predict the Cu recovery, respectively. The correlation coefficient and mean squared error values for the testing sets for Cu recovery using GANN and ANN were 0.96, 0.02 and 0.92, 66.67, respectively. The correlation coefficient and mean squared error values of the testing sets in GANN were less than those in ANN that show the more efficiency of GANN for this study. The results showed that the proposed model, according to parameters affecting the recovery of copper during column leaching, can be used to predict the Cu recovery with a reasonable error.

References

[1] Padilla G A, Cisternas L A, Cueto J Y. On the optimization of heap leaching [J]. Minerals Engineering, 2008, 21: 673-678.

[2] Shayestehfar M, Nasab S K, Mohammadalizadeh H. Mineralogy, petrology, and chemistry studies to evaluate oxide copper ores for heap leaching in Sarcheshmeh copper mine, Kerman, Iran [J]. Journal of Hazardous Materials, 2008, 154: 602-612.

[3] Wu A, Yin S, Yang B, Wang J, Qiu G. Study on preferential flow in dump leaching of low-grade ores [J]. Hydrometallurgy, 2007, 87: 124-132.

[4] Yorio Cd, Betancourt E, Vivas R, Rus J. Ni, Co recovery study and Fe by acid leaching in columns [J]. Revista de Metalurgia, 2006, 42: 41-48.

[5] PETERSEN J, DIXON D. Modelling zinc heap bioleaching [J]. Hydrometallurgy, 2007, 85: 127-143.

[6] Leahy M, Davidson M, Schwarz M. A model for heap bioleaching of chalcocite with heat balance: Mesophiles and moderate thermophiles [J]. Hydrometallurgy, 2007, 85: 24-41.

[7] Mellado M E, Cisternas L A. An analytical–numerical method for solving a heap leaching problem of one or more solid reactants from porous pellets [J]. Computers & Chemical Engineering, 2008, 32: 2395-2402.

[8] Mellado M E,  E D, Cisternas L A. On the optimization of flow rates on copper heap leaching operations [M]. International Journal of Mineral Processing, 2011, 101: 75-80.

[9] SOHN H Y, WADSWORTH M E. Rate processes of extractive metallurgy [M]. Springer Science & Business Media, 2013.

[10] Ekmekyapar A, Oya R,  A. Dissolution kinetics of an oxidized copper ore in ammonium chloride solution [J]. Chemical and Biochemical Engineering Quarterly, 2003, 17: 261-266.

[11] Dixon D G, Hendrix J L. A mathematical model for heap leaching of one or more solid reactants from porous ore pellets [J]. Metallurgical Transactions B, 1993, 24: 1087-1102.

[12] Mellado M E,  E D, Cisternas L A. Stochastic analysis of heap leaching process via analytical models [J]. Minerals Engineering, 2012, 33: 93-98.

[13] Veglio F, Trifoni M, Abbruzzese C, Toro L. Column leaching of a manganese dioxide ore: A study by using fractional factorial design [J]. Hydrometallurgy, 2001, 59: 31-44.

[14] Chelgani S C, Jorjani E. Artificial neural network prediction of Al₂O₃ leaching recovery in the Bayer process—Jajarm alumina plant (Iran) [J]. Hydrometallurgy, 2009, 97: 105-110.

[15] Chelgani S C, Shahbazi B, Rezai B. Estimation of froth flotation recovery and collision probability based on operational parameters using an artificial neural network [J]. International Journal of Minerals, Metallurgy, and Materials, 2010, 17: 526-534.

[16] Amnieh H B, Siamaki A, Soltani S. Design of blasting pattern in proportion to the peak particle velocity (PPV): Artificial neural networks approach [J]. Safety Science, 2012, 50: 1913-1916.

[17] Khandelwal M, Singh T. Prediction of blast-induced ground vibration using artificial neural network [J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46: 1214-1222.

[18] Patterson D W. Artificial neural networks: Theory and applications [M]. Prentice Hall PTR, 1998.

[19] Turnbull J P. Neural network PC tools: A practical guide [J]. Journal of Clinical Neurophysiology, 1992, 9: 160.

[20] Vose M D. The simple genetic algorithm: Foundations and theory [M]. Vol. 12. MIT Press, 1999.

[21] Hamer W J. Theoretical mean activity coefficients of strong electrolytes in aqueous solutions from 0 to 100 °C [R]. DTIC Document, 1968.

[22] Svedensten P, Evertsson C M. Crushing plant optimisation by means of a genetic evolutionary algorithm [J]. Minerals Engineering, 2005, 18: 473-479.

[23] Farzanegan A, Vahidipour S. Optimization of comminution circuit simulations based on genetic algorithms search method [J]. Minerals Engineering, 2009, 22: 719-726.

[24] ShopovSohna E G, Vaklieva-Bancheva N G. BASIC—A genetic algorithm for engineering problems solution [J]. Computers & Chemical Engineering, 2006, 30: 1293-1309.

[25] Yasin Y, Ahmad F B H, Ghaffari-Moghaddam M, Khajeh M. Application of a hybrid artificial neural network– genetic algorithm approach to optimize the lead ions removal from aqueous solutions using intercalated tartrate-Mg–Al layered double hydroxides [J]. Environmental Nanotechnology, Monitoring & Management, 2014, 1: 2-7.

[26] Gupta J N, Sexton R S. Comparing backpropagation with a genetic algorithm for neural network training [J]. Omega, 1999, 27: 679-684.

[27] Li C, Yang Z, Yan H, Wang T. The application and research of the GA-BP neural network algorithm in the MBR membrane fouling. Abstract and Applied Analysis [M]. Hindawi Publishing Corporation, 2014.

[28] Martínez-Morales J D, Palacios-Hernández E R, Velázquez-Carrillo G A. Artificial neural network based on genetic algorithm for emissions prediction of a SI gasoline engine [J]. Journal of Mechanical Science and Technology, 2014, 28: 2417-2427.

采用人工神经网络基因复合算法预测氧化铜矿柱浸工艺铜浸出率

Fatemeh Sadat HOSEINIAN¹, Aliakbar ABDOLLAHZADE^1,2, Saeed Soltani MOHAMADI², Mohsen HASHEMZADEH³

1. Department of Mining & Metallurgical Engineering, Amirkabir University of Technology, Tehran, Iran;

2. Department of Mining Engineering, University of Kashan, Kashan, Iran;

3. Department of Chemical and Materials Engineering, University of Alberta Edmonton, Alberta T6E 2H8, Canada

摘  要：采用人工神经网络(ANN)以及人工神经网络和基因复合(GANN)算法来优化氧化铜矿柱浸工艺参数。采用三种高度的浸矿柱(2，4，6 m)和尺寸为<25.4 mm和<50.8 mm的两种矿物来进行浸出实验。在台架实验规模下，对浸矿柱高度、矿粒尺寸、硫酸流速、浸出时间等工艺参数对铜浸出率的影响进行研究，对浸出条件进行优化以得到最大的浸出率。研究结果表明，铜的浸出率随硫酸流速和浸出时间的增加而增加，随矿粒尺寸和浸矿柱高度的减小而增加。对人工神经网络(ANN)、人工神经网络和基因复合(GANN)算法的效率进行了比较，结果表明，人工神经网络和基因复合(GANN)算法比人工神经网络(ANN)算法更有效。采用新提出的算法模型来预测铜的浸出率误差更低。

关键词：浸出；氧化铜矿；浸出率；人工神经网络；基因算法

(Edited by Sai-qian YUAN)

Corresponding author: Fatemeh Sadat HOSEINIAN; Tel: +98-21-64542940; Fax: +98-21-66405846; E-mail: f_hoseinian@aut.ac.ir

DOI: 10.1016/S1003-6326(17)60076-1