DOI: 10.11817/j.issn.1672-7207.2015.01.034

不同土体中水泥-水玻璃浆液的扩散规律

刘强¹，张可能¹，陈宾²，黎永索³

 (1. 中南大学 地球科学与信息物理学院，湖南 长沙，410083；

2. 湘潭大学 能源工程学院，湖南 湘潭，411005；

3. 中南大学 土木工程学院，湖南 长沙，410083)

摘要：为研究不同土体中水泥-水玻璃浆液扩散规律，基于浆液劈裂土体形成的裂缝形状和宾汉流体在平板裂缝中的流变方程，推导出不同土体中水泥-水玻璃浆液黏度、流量、注浆压力差、浆液扩散距离的计算公式，计算分析不同土体中水泥-水玻璃浆液的黏度、注浆压力以及裂隙高度对浆液扩散距离的影响。研究结果表明：浆液扩散距离随浆液黏度的增大呈非线性减小，随注浆压力的增大呈非线性增大，裂隙高度增大使浆液扩散距离迅速增大；通过注浆后工程现场取芯试验对计算结果进行分析，验证了不同土体中浆液扩散距离和劈裂缝高度的关系。

关键词：水泥-水玻璃浆液；宾汉体浆液；劈裂注浆；扩散距离

中图分类号：TU441             文献标志码：A         文章编号：1672-7207(2015)01-0255-06

Diffusion law of cement-sodium silicate grout in different soils

LIU Qiang¹, ZHANG Keneng¹, CHEN Bin², LI Yongsuo³

 (1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;

2. School of Energy Engineering, Xiangtan University, Xiangtan 411005, China;

3. School of Civil Engineering, Central South University, Changsha 410083, China)

Abstract: In order to study different soil cement-silicate grout diffusion laws, the soil and Bingham rheological equation in the flat-panel cracks, mathematical formulas for calculating the grout viscosity, grouting flow rate, grouting pressure difference and diffusion distance of the cement-silicate grout in different soils were deduced based on the shapes of the fractures formed during the grout splits. With the formulas, the effects of grout viscosity, grouting pressure and fracture height of the cement-silicate grout on the grout diffusion distance in different soils were analyzed. The results show that the grout diffusion distance nonlinearly decreases with the increase of the gout viscosity, and nonlinearly increases with the increase of the grouting pressure. Furthermore, with the increase of the fracture height, the grout diffusion distance increases rapidly. The relationship between the grout diffusion distance and the fracture height in different soils are verified when the calculated results are compared with the results obtained from field core extraction experiments.

Key words: cement-silicate grout; Bingham grout; fracture grouting; diffusion distance

随着注浆技术在工程中的应用范围不断扩大，水泥-水玻璃浆液也在工程中得到广泛应用，但在不同土体中的扩散规律差别较大，注浆参数的选取也不一样。目前，大多数注浆理论主要针对单液浆进行研究，如杨志全等^[1]对黏度时变性宾汉体浆液的柱-半球形渗透注浆机制进行了研究；王作成等^[2-6]对水泥浆在岩体裂隙内的扩散规律进行了研究，研究对象也以注浆压力和浆液成分及其流型为主；吕洪予等^[7-9]对水泥浆在劈裂的土体裂缝中的扩散规律进行了研究；杨秀竹等^[10]推导了宾汉体浆液在砂土中进行渗透注浆时扩散半径的计算公式。这些研究主要针对单一土体中单液浆的扩散规律，很少考虑不同土体中水泥-水玻璃液浆扩散规律。为此，本文作者基于浆液在土体中劈裂时裂缝扩展形状和水泥-水玻璃浆液宾汉体在平板裂缝中流变方程，对不同土体中水泥-水玻璃双液注浆中注浆压力、土体劈裂缝高度、浆液扩散距离等因素之间的关系进行研究，以便为不同土体中水  泥-水玻璃双液注浆设计和施工提供依据。

1  土体劈裂注浆模型

1.1  基本假定

对土体劈裂注浆进行以下基本假定：1) 土体为各向同性体，1次劈裂形成足够长的劈裂缝，仅考虑单一水平劈裂浆脉的情况；2) 浆液为宾汉流体，浆液在平板缝隙内的流速较小且恒定，流体运动符合水力平衡条件；3) 浆液在注浆扩散过程中流型不变，考虑浆液流变参数(如黏度)的时变性；4) 双液浆属于时变性的宾汉流体^[11]，忽略裂隙面上的粗糙程度，浆液在裂隙中的流动为层流。

1.2  土体劈裂注浆模型

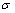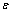在土体劈裂注浆过程中，假定水泥-水玻璃浆液在土体中劈裂形成高度恒定的裂缝，用二维解析方法建立裂缝宽度的计算模型。二维解析方法是指应力、应变和位移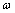只受空间3个坐标变量中的2个变量影响，且应力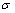或应变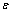在某一个坐标方向为0，可以构成平面应力或平面应变条件。根据线弹性断裂力学Ⅰ型裂纹在平面应变(或平面应力)状态下的位移场W(x)关系式^[12-13]为

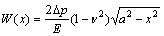         (1)

式中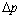：为地层裂隙内的浆液压力差，MPa；E为土体的压缩模量，MPa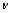；为土体的泊松比；a为劈裂裂缝半长，m；x为浆液流动半高度，m。

假定浆液形成的劈裂缝断面主要为矩形，且劈裂缝高度一定，将注浆劈裂缝视为在缝长度方向连续排列的许多个Ⅰ型贯穿裂纹的合成，见图1。将式(1)用于任意1个分裂纹可得缝宽方程：

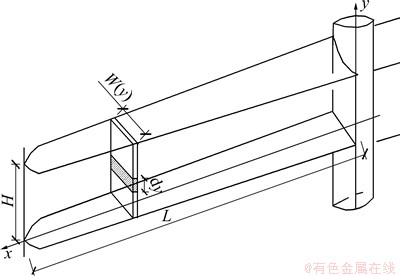
图1  恒缝高矩形断面劈裂缝空间形态

Fig. 1  Morphology of a rectangular fracture with constant height

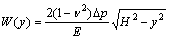         (2)

式中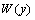：为注浆劈裂缝的宽度，m；H为劈裂缝的最终厚度，也是劈裂浆脉的厚度，m；y为劈裂缝瞬时厚度，m。

土体加固注浆较常用的水泥-水玻璃浆液为宾汉体浆液^[11]，其流变方程表示为

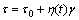                 (3)

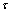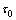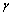式中：为剪切应力(Pa)；为流体流动的屈服剪切力(Pa)，通过试验确定；为时变性浆液黏度(mPa·s)；为剪切速率，

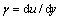                 (4)

劈裂缝中浆液沿x轴正向层流运动，取注浆孔为对称轴，x轴为流体裂缝单元。流体微元段上两端压力为p+dp和p，微元段上浆液压差为dp。流体单元上下表面所受剪切应力为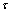，其方向向左，如图2所示，与流速方向相反。在不计重力的情况下，由流体单元水力平衡条件得

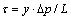                (5)

式中：L为浆液扩散距离，m。

从式(5)可知流体单元表面的剪切应力τ与单元高度y和压力梯度dp/dL成正比。式(3)对牛顿体和非牛顿体均适用。由式(3)~(5)可得

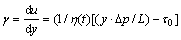       (6)

对于宾汉流体，当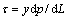≤ 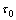时，流体单元不受剪切力作用，即在矩形缝隙中存在1个临界高度H₀。当0≤y≤H₀时，流体相对于邻层流体静止，呈活塞式整体运动，速度u=u₀；而在H₀≤y≤H时，流体相对于临层处于运动状态。根据式(6)有

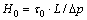                (7)

当平板缝隙中的流体流动为层流时，H₀≤y≤H，对式(6)分离变量，并考虑边界条件y=±H/2时，u=0，则

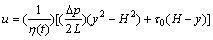     (8)

当0≤y≤H₀时，流体呈活塞式整体运动，

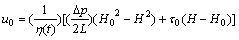    (9)

缝隙中的流体速度为图2所示截头抛物面形状，其流量为通过剪切区与活塞区流量之和。考虑注浆过程中浆液对土体的劈裂作用，通过劈裂缝的单位时间流量为

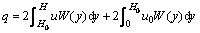     (10)

将式(2)，(8)和(9)代入式(10)后积分得

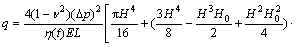
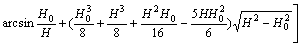 (11)

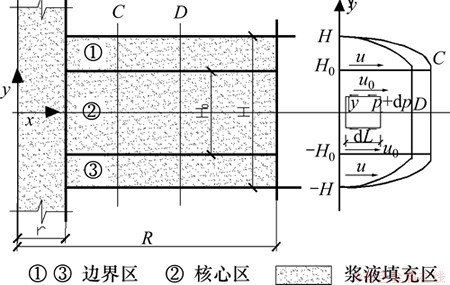
图2  宾汉体浆液在平板窄缝中流动示意图

Fig. 2  Sketch map of Bingham grout flow in narrow gap of plate

2  计算分析

不同的土体具有不同的压缩模量和泊松比，选取注浆工程中经常遇见的碎石土、砂土、粉土、黏土和淤泥质土共5种典型土体，按式(11)对这5种土体的劈裂注浆机理进行计算分析，分析不同土体中的劈裂注浆浆液的扩散规律。各种土体参数根据文献[14]中的土体物理力学指标经验参数取其平均值，各土层压缩模量和泊松比参数见表1。

表1 不同土体的压缩模量和泊松比

Table 1  Different soil compression modulus and poisson ratio

2.1  注浆时间对浆液黏度的影响

根据文献[11, 15]中提出的当水灰比(即水与水泥质量比)为1:1时，不同水泥浆和水玻璃体积比浆液的黏度随时间变化的关系式，拟合出水泥-水玻璃浆液黏度随时间变化的曲线，如图3所示。从图3可以看出：水泥-水玻璃浆液为黏时变流体，且随着时间的增长，其黏度逐渐变大。

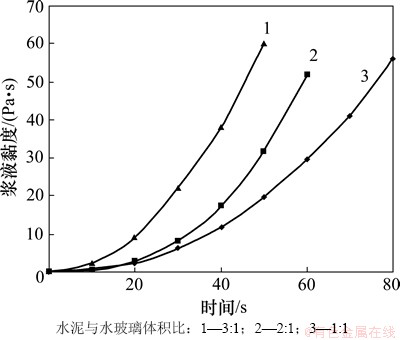
图3  水泥-水玻璃浆液黏度随时间变化曲线

Fig. 3  Relationship between cement-silicate grout viscosity and time

2.2  不同土体中浆液黏度对浆液扩散距离的影响

根据在不同土体中注浆后现场取芯情况，浆脉厚度H在2~50 mm之间。对于矩形劈裂缝的理想平面流模型，假定在单裂缝单位时间内浆液流量q=0.2 L/s，注浆压力差△p=1.0 MPa时，取劈裂缝厚度H=0.01 m，H₀=H/2。根据式(11)计算出不同土体中水泥-水玻璃浆液黏度对扩散距离的影响，计算结果如图4所示。

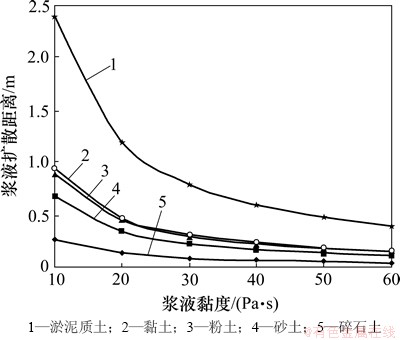
图4  水泥-水玻璃浆液黏度对扩散距离的影响

Fig. 4  Effect of cement-silicate grout viscosity on diffusion distance

从图4可见：随着水泥-水玻璃浆液黏度的增大，劈裂缝中浆液扩散的距离逐渐减小，其中浆液的黏度与浆液扩散距离呈反比关系。在其他条件一定的情况下，浆液在碎石土中扩散的距离最短，而在淤泥质土等软弱土体中扩散距离较大。因此，在注浆过程中，考虑到水泥-水玻璃浆液黏度的时变性，为保证注浆所需的有效扩散距离，在不同土体内，应采取不同的浆液混合方式进行注浆，在碎石土、砂土、粉土和黏土中，一般采用孔底混合方式，可使浆液扩散的距离更大；而在软土中，一般采用孔口混合即可满足浆液的有效扩散距离，这与实际注浆工程中的情况相吻合。

2.3  不同土体内注浆压力对浆液扩散半径的影响

对于矩形劈裂缝的理想平面流模型，假定在q= 0.2 L/s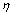，=40 Pa·s时，取H₀=H/2，H=0.01 m，根据式(11)计算出不同土体内水泥-水玻璃浆液注浆压力差对浆液扩散距离的影响，计算结果如图5所示。

从图5可见：随着劈裂缝中浆液压力差的增大，浆液扩散距离也逐渐增大，其中浆液的扩散距离与劈裂缝中的注浆压力的平方呈正比关系。在其他条件一定的情况下，浆液在碎石土中扩散的距离最小，在淤泥质土中扩散的距离较大，表明浆液在劈裂缝中流动时，在较硬的土体(如碎石土)中扩散所需阻力较大，在软土(淤泥质土)中，浆液扩散所需阻力较小；在注浆设计中，为确保有效的扩散距离，较硬土中所需的注浆压力要适当增大，而在软土中所需的注浆压力  较小。

2.4  浆液扩散距离对劈裂缝高度的影响

对于矩形劈裂缝的理想平面流模型，假定在q= 0.2 L/s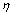，=40 Pa·s时，H₀=H/2，△p=1.0 MPa，根据式(11)对不同土体内劈裂缝高度对浆液扩散距离的影响规律进行计算分析，劈裂缝高度H对扩散距离的影响如图6所示。

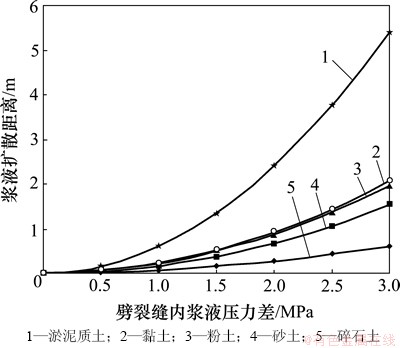
图5  注浆压力对扩散距离的影响

Fig. 5  Effect of grouting pressure on diffusion distance

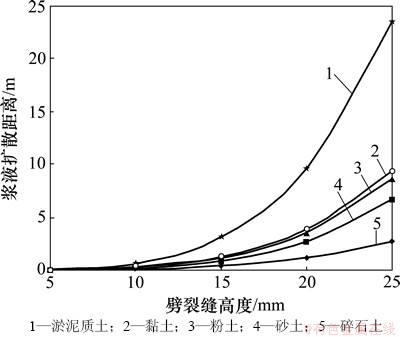
图6  浆液扩散距离对劈裂缝高度的影响

Fig. 6  Grout diffusion distance influence on fracture height

由图6可知：劈裂缝的高度H对浆液扩散距离的影响显著；随着劈裂缝的高度H的增大，浆液扩散距离不断增大。在注浆时，浆液注入劈裂缝中，并挤压劈裂缝两侧的土体，劈裂缝宽度逐渐增大，裂缝扩展，浆液扩散距离增大。由于硬土(如碎石土)土体压缩模量较大，劈裂缝两侧土体难以被压缩挤密，裂缝难以扩展，浆液扩散距离较小，劈裂缝中充填的浆脉厚度较薄；而软土(如淤泥质土)土体压缩模量较小，劈裂缝两侧土体容易被压缩挤密，裂缝容易扩展，劈裂缝中充填的浆脉厚度较厚，浆液扩散距离较大。因此，在软土或松散土体等高压缩性土体中注浆对土体改良效果将会更好，而在碎石土等硬土中，注浆对土体改良的效果差一些。

3  工程案例分析

3.1  碎石土劈裂注浆

注浆工程为某高速公路边坡桥梁桩基桩侧注浆，桩侧地层较均匀，主要为碎石土，土体压缩模量为25 MPa，泊松比为0.2，现场主要采用水灰比为1:1的水泥-水玻璃浆液进行桩侧注浆，注浆压力为2.0 MPa。注浆完成后，在注浆地层中距离注浆孔1.5 m的位置进行取样分析，按本文的计算公式计算，在扩散距离为1.5 m处，劈裂缝厚度计算值为14.5 mm。根据现场取芯可以看出：芯样中含有厚8~13 mm的水泥浆脉(见图7)，浆脉厚度与计算结果基本吻合。由图7可知：浆液在土体中形成浆脉骨架，对桩周土体进行挤密和充填，提高桩周土体的强度。

图7  碎石土注浆后现场取芯芯样

Fig. 7  Gravel soil core after grouting

3.2  黏土劈裂注浆

注浆工程为某高速公路路基岩溶塌陷加固注浆，路基主要为回填黏土，土体压缩模量E为6 MPa，泊松比为0.32。为控制浆液的扩散距离，现场主要采用水泥-水玻璃浆液注浆，注浆压力为1.0 MPa。注浆完成后，在注浆地层中距离注浆孔1.0 m的位置进行取样分析，按本文的计算公式计算，在扩散距离1.0 m处，劈裂缝厚度约为7.4 mm。根据现场取芯可以看出：芯样中含有厚4~6 mm的水泥浆脉(见图8)。从芯样中浆脉厚度与理论计算值对比分析，注浆后土体被水泥浆液劈裂形成浆脉骨架厚度与理论计算值相近。浆脉对回填土体进行挤密和充填，提高了路基土体的强度。

图8  黏土注浆后现场取芯芯样

Fig. 8  Clay core after grouting

4  结论

1) 水泥-水玻璃浆液属于宾汉流体，满足宾汉流体本构方程。且水泥-水玻璃浆液是时变性流体，浆液黏度随时间逐渐增大。

2) 在结合浆液在土体中劈裂缝形状和宾汉流体在平板裂缝中流变方程的基础上，提出了不同土体内浆液黏度、流量、注浆压力差、浆液扩散距离的计算公式，其计算方法考虑了在不同土体中注浆时浆液的扩散规律，可以在不同土体注浆工程设计和施工中  应用。

3) 浆液的黏度、注浆压力、浆液扩散距离、裂隙高度、土体的压缩模量和泊松比是劈裂注浆的几个关键因素。浆液扩散距离与浆液黏度成反比，并随着浆液黏度的增大而减小。水泥-水玻璃浆液在淤泥质土中扩散距离较远，浆液可在孔口混合，在碎石土中扩散距离较小，浆液应在孔底混合。浆液在淤泥质土中扩散时劈裂缝内浆液压力损失较小，在碎石土中扩散时劈裂缝内压力损失较大，在软土中注浆浆液对土体的注浆效果更好。增大裂隙高度能增大浆液的扩散距离，在淤泥质土中，浆液劈裂缝高度对浆液扩散距离影响较大，浆液能形成更厚的浆脉，在碎石土中，浆液劈裂缝对扩散距离的影响较小，形成的浆脉较薄。

4) 通过对不同土体内注浆后取芯分析，在取芯位置浆脉计算厚度与芯样浆脉实际厚度相近。

参考文献：

[1] 杨志全, 侯克鹏, 郭婷婷. 黏度时变性宾汉体浆液的柱-半球形渗透注浆机制研究[J]. 岩土力学, 2011, 32(1): 2697-2703.

YANG Zhiquan, HOU Kepeng, GUO Tingting. Study of column-hemispherical penetration grouting mechanism based on Bingham fluid of time-dependent behavior of viscosity[J]. Rock and Soil Mechanics, 2011, 32(1): 2697-2703.

[2] 王作成, 李奋强. 复杂煤矿区帷幕注浆浆液及其隔水机理[J]. 中南大学学报(自然科学版), 2013, 44(2): 778-784.

WANG Zuocheng, LI Fenqiang. Slurry water curtain grouting and its mechanism in complex coal mine area[J]. Journal of Central SouthUniversity (Science and Technology), 2013, 44(2): 778-784.

[3] 孙峰, 张顶立, 陈铁林. 基于流体时变性的隧道劈裂注浆机理研究[J]. 岩土工程学报, 2011, 33(1): 88-93.

SUN Feng, ZHANG Dingli, CHEN Tielin. Fracture grouting mechanism in tunnels based on time-dependent behaviors of grout[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 88-93.

[4] Kelessidis V C, Maglione R, Tsamantaki C. Optimal determination of rheological parameters for Herschel-Bulkley drilling fluids and impact on pressure drop, velocity profiles and penetration rates during drilling[J]. Journal of Petroleum Science and Engineering, 2006, 5(3): 203-224.

[5] Huilgol R R, You Z. Application of the augmented Lagrangian method to steady pipe flows of Bingham Cass on and Herschel-Bulkley fluids[J]. Journal of Non-Newtonian Fluid Mech, 2005, 12(8): 126-143.

[6] 刘人太, 李术才, 张庆松. 岩溶裂隙水探查方法优化与工程治理研究[J]. 岩土力学, 2011, 32(4): 1096-1107.

LIU Rentai, LI Shucai, ZHANG Qingsong. Research on optimization of karst fissure water exploration methods and engineering countermeasures[J]. Rock and Soil Mechanics, 2011, 32(4): 1096-1107.

[7] 吕洪予, 方开泽, 王洪恩. 土坝坝体劈裂灌浆浆液固结分析[J]. 岩土工程学报, 1994, 16(5): 16-23.

L Hongyu, FANG Kaize, WANG Hongen. Analysis of slurry consolidation of splitting groutof earth dam[J]. Chinese Journalof Geotechnical Engineering, 1994, 16(5): 16-23.

[8] 邹金锋, 李亮, 杨小礼. 劈裂注浆扩散半径及压力衰减分析[J]. 水利学报, 2006, 37(3): 314-319.

ZOU Jinfeng, LI Liang, YANG Xiaoli. Penetration radius and pressure attenuation law in fracturing grouting[J]. Journal of Hydraulic Engineering, 2006, 37(3): 314-319.

[9] 章敏, 王星华, 汪优. Herschel-Bulkley浆液在裂隙中的扩散规律研究[J]. 岩土工程学报, 2011, 33(5): 815-819.

ZHANG Min, WANG Xinghua, WANG You. Diffusion of Herschel-Bulkley slurry in fractures[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(5): 815-819.

[10] 杨秀竹, 王星华, 雷金山. 宾汉体浆液扩散半径的研究及应用[J]. 水利学报, 2004, 35(6): 75-79.

YANG Xiuzhu, WANG Xinghua, LEI Jinshan. Study on routing diffusion radius of bingham fluids[J]. Journal of Hydraulic Engineering, 2004, 35(6): 75-79.

[11] 刘人太. 水泥基速凝桨液地下工程动水注浆扩散封堵机理及应用研究[D]. 济南: 山东大学土建与水利学院, 2012: 52-55.

LIU Rentai. Study on diffusion and plugging mechanism of quick setting cement based slurry in underground dynamic water grouting and its application[D]. Jinan: Shandong University. School of Civil Engineering, 2012: 52-55.

[12] 乌效鸣, 屠厚泽. 煤层水力压裂典型裂缝形态分析与基本尺寸确定[J]. 中国地质大学学报, 1995, 20(1): 112-116.

WU Xiaoming, TU Houze. Morphological analysis and geometrical size determination of representative hydraulic fractures in coal seam[J]. Journal of China University of Geosciences, 1995, 20(1): 112-116.

[13] Ewalds H L, Wanhill R J H. 断裂力学[M]. 朱永昌, 译. 北京: 北京航空航天大学出版社, 1988: 172-185.

Ewalds H L, Wanhill R J H. Fracture mechanics[M]. ZHU Yongchang, trans. Beijing: Beihang University Press, 1988: 172-185.

[14] 工程地质手册编委会. 工程地质手册[M]. 4版. 北京: 中国建筑工业出版社, 2006: 159-160.

Handbook Committee of Engineering Geology. Engineering geology manual[M]. 4th ed. Beijing: China Building Industry Press, 2006: 159-160.

[15] 阮文军. 注浆扩散与浆液若干基本性能研究[J]. 岩土工程学报, 2005, 27(1): 69-73.

RUAN Wenjun. Research on diffusion of grouting and basic properties of grouts[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(1): 69-73.

(编辑  陈灿华)

收稿日期：2014-01-12；修回日期：2014-03-14

基金项目(Foundation item)：国家自然科学基金资助项目(51408069)；湖南省教育厅一般研究项目(11C0246)；2012年度湖南省高等学校科学研究项目(12C0377) (Project(51408069) supported by the National Natural Science Foundation of China; Project(11C0246) supported by the General Research Project, Education Department of Hunan Province; Project(12C0377) supported by Science Research Project of Higher Education of Hunan Province in Year 2012)

通信作者：刘强，博士研究生，从事注浆加固及地基处理研究；E-mail: 283073337@qq.com