DOI: 10.11817/j.issn.1672-7207.2015.12.042
基于恒风速虚拟风洞实验的碟式太阳能聚光器风动载荷
鄂加强1, 2,王红林2,刘腾1, 2,左威2,张庆玲2,苏秀超2
(1. 湖南大学 汽车车身先进设计制造国家重点实验室,湖南 长沙,410082;
2. 湖南大学 机械与运载工程学院,湖南 长沙,410082)
摘要:针对碟式太阳能聚光器最佳避风姿势问题,采用恒风速虚拟风洞实验方法对不同姿态和不同风速下的碟式太阳能聚光器风动载荷进行仿真分析。研究结果表明:在靠近来流方向处碟式太阳能聚光器总压力较大,而远离来流方向处其总压力相对较小,且碟式太阳能聚光器反射面的最大压强随恒风速的增大而不断增加;当风速由v=15 m/s增大到v=25 m/s时,碟式太阳能聚光器所受风力和风力矩的最大幅值至少增加了110%。
关键词:聚光器;虚拟风洞实验;风动载荷;太阳能
中图分类号:TK514 文献标志码:A 文章编号:1672-7207(2015)12-4700-07
Wind loadings on dish solar concentrator based on virtual wind tunnel experiment with constant wind
E Jiaqiang1, 2, WANG Honglin2, LIU Teng1, 2, ZUO Wei2, ZHANG Qingling2, SU Xiuchao2
(1. State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University, Changsha 410082, China;
2. College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China)
Abstract: In order to solve the problem of the optimal shelter posture of dish solar concentrator, virtual wind tunnel experimental with constant wind was implemented for simulation analysis of the aerodynamic load on dish solar concentrator at different attitudes and wind speeds. The results show that the dish solar concentrator total pressure close to the flow direction is relatively higher and the dish solar concentrator total pressure away from the flow direction is relatively lower. The maximum pressure of dish solar concentrator reflective surface increases with the addition of constant wind speed. The amplitudes of the wind force and torque on the dish solar concentrator increase by 110% at least when the wind speed increases from 15 m/s to 25 m/s.
Key words: concentrator; virtual wind tunnel experiment; aerodynamic load; solar energy
太阳能作为可再生能源与传统能源相比适用范围广且效益显著[1],并拥有广阔的发展前景[2]。对于碟式太阳能聚光器而言,风的扰动作用是最大的不确定载荷,而影响碟式太阳能聚光器风动载荷最重要部位是反射面。由于反射面迎风面积大,空气阻力系数也大,因此导致碟式太阳能聚光器在某些状态下的风载十分巨大。由于导致碟式太阳能聚光器相对于气流方向变化的不确定性,故气流对碟式太阳能聚光器的风动载荷不是一个恒定的载荷。而且气流流过聚光器时,会在反射面之后形成脱体漩涡,相当于给聚光器施加了脉动激振力,容易导致碟式太阳能聚光器振动,甚至引起破坏性的共振。因此,对各种工况下的碟式太阳能聚光器受到的风动载荷特性研究显得十分重要。20世纪90年代以来,国内外研究工作者关于碟式太阳能热发电系统的研究主要集中在提高吸热器能量转化效率[3-6]、聚光器聚光效率[7-9]等方面,而没有针对碟式太阳能热发电系统推广应用的风激振动对碟式太阳能聚光器风载压强分布与模态影响机理进行研究。风洞试验是常用的计算结构风载荷的方法,成本高、周期长,而数值仿真方法可以快速准确地得到模型受风作用时的模型风效应情况,避免风洞试验由于忽略细节而引起的计算误差而显示出蓬勃生机[10-12]。国内外学者也提出多种风载荷计算方法[13-15]。因此,本文作者采用简化的物理模型和高精度的数值算法,在恒风速虚拟风洞实验下的碟式太阳能聚光器进行风动载荷分析,获得碟式太阳能聚光器风动载荷分布,为改进碟式太阳能聚光器的结构以及对工程实践中的最佳避风姿势问题提供理论依据。
1 风动载荷仿真模型
1.1 数学模型
碟式太阳能聚光器工作在大气边界层的风场中,由于气流在大气边界层中的流动属于湍流,为低速、不可压缩的黏性牛顿流体。故对碟式太阳能聚光器流体区域进行数值模拟时,不考虑热交换,即不考虑能量方程。
1) 质量守恒方程为
 (1)
(1)
2) 动量守恒方程为

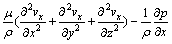 (2)
(2)
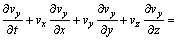
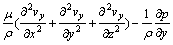 (3)
(3)
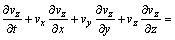
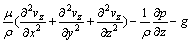 (4)
(4)
3) 湍流方程模型为
 (5)
(5)
式中:vx,vy和vz分别为风速度在x,y和z方向的分量,m/s;t为时间,s;μ为空气动力黏度,Pa·s,且μ=μ0+μT,μ0为空气分子黏性系数,μT=cμρK2/ε,cμ为与K-ε方程有关的常数,K为湍动能,ε为湍动能耗散率;ρ为空气密度,kg/m3;p为绝对压强,Pa;σk为湍流动能的有效Prandtl数;GK=μT( uj/
uj/ xi+
xi+ ui/
ui/ xj) (
xj) ( uj/
uj/ xi)。
xi)。
 (6)
(6)
式中:σε 为湍流动能耗散率的有效Prandtl数;c1和c2为与K-ε方程有关的常数。
数学模型中的有关常数如表1所示。
表1 数学模型常数
Table 1 Constant of model

1.2 力学模型
风力F与空气密度ρ、风速v、空气的黏性μ、碟式太阳能聚光器的直径D等有关,故风力F可表示为
 (7)
(7)
用因式分解法可得:
 (8)
(8)
因为碟式太阳能聚光器的D2正比于碟式太阳能聚光器的特征面积A(即D2∝A),且雷诺数Re=ρvD/μ,故式(8)可表示为
 (9)
(9)
式中:CF为风力系数,CF=f(Re)。
对于碟式太阳能聚光器,当风向不同时,风力也不同。为计算方便,无论风向如何,式(9)中的A取相同值,例如取高度角β=0o、方位角α=0o时的最大面积,而仅仅是风力系数随风向而变。
图1所示为碟式太阳能聚光器受风载荷作用后的受力图。一般情况下,碟式太阳能聚光器所受风力可分解为侧力Fx、阻力Fy和升力Fz:
Fx=0.5ρv2ACx (10)
Fy=0.5ρv2ACy (11)
Fz=0.5ρv2ACz (12)
式中:Cx为侧力系数;Cy为阻力系数;Cz为升力系数。
此外,碟式太阳能聚光器受风力作用时还会产生风力矩。类似地,碟式太阳能聚光器所受风力矩可表示为

图1 碟式太阳能聚光器受力图
Fig. 1 Force diagram of dish solar concentrator
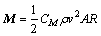 (13)
(13)
式中:CM为风力矩系数;R为碟式太阳能聚光器半径,m。
当碟式太阳能聚光器受沿Y轴风向作用时,风力矩在一般情况下可分解为俯仰力矩Mx、翻滚力矩My和方位力矩Mz:
Mx=0.5CMxρv2AR (14)
My=0.5CMyρv2AR (15)
Mz=0.5CMzρv2AR (16)
式中: 为俯仰力矩系数;
为俯仰力矩系数; 为翻滚力矩系数;
为翻滚力矩系数; 为方位力矩系数。
为方位力矩系数。
1.3 物理模型
碟式太阳能聚光器物理模型如图2所示。当风对碟式太阳能聚光器进行绕流时,碟式太阳能聚光器相当于处于完全开口的流动风场中。而风对碟式太阳能聚光器的作用存在于一定的范围内,因此在建立碟式太阳能聚光器计算流体域时给定与实际相对应的边界条件。碟式太阳能发电系统聚光器直径约为18 m,厚度为0.28 m,为保证气流在流体域内的流动达到充分发展的状态,流体域的长度约为聚光器的10倍,流体域的宽度和高度约为碟式太阳能发电系统聚光器的5倍,经过多次建模仿真,确定流体域长×宽×高为170 m×80 m×80 m,模型中心距地面高度为10 m,风的入口距模型中心距离为55 m,如图3所示。
对模型进行设定,将空气看作连续介质、无压缩黏性流体。网格的类型和网格的数量对计算结果的准确性有很大的影响。对该模型的流体区域采用的是多面体网格,非结构网格具有很好的灵活性和适应性,易于进行网格自适应。为了更准确地模拟聚光器周围流场特性,对聚光器周围区域有远及近逐步加密。

图2 碟式太阳能聚光器物理模型
Fig. 2 Physical model of dish solar concentrator

图3 碟式太阳能聚光器计算域模型
Fig. 3 Computational domain model of dish solar concentrator
1.4 仿真条件设定
设置边界条件前需对模型的流体域进行设置,流体域中所选流体为空气,气温为常温且绝热,参考压强为100 kPa,且采用3种以下方式确定模拟风洞实验初始条件和边界条件:
1) 入口初始条件和边界条件:该区域的流体为不可压缩流体流动,入口初始风速分为恒定风速,该区域的流体流动为不可压缩流体流动,入口风速v分别为15,20和25 m/s。
2) 出口边界条件:出口处的边界条件采用压强出口边界条件,压强为100 kPa。
3) 壁面条件:流体域表面和聚光器表面,wall是一种限定流体域和固体域的边界条件。壁面条件的粗糙度设置为光滑。对于黏性流体,采用黏附条件,即认为壁面处流体速度与壁面该处的速度相同,无滑移壁面的速度为0 m/s,壁面处流体速度为0 m/s。聚光器表面和地面固定不动,不发生移动,所以采用无滑移的壁面条件;而流体域的顶面和前后面采用滑移边界条件。
1.5 控制方程离散化与求解
采用有限差分法对碟式太阳能聚光器风动载荷模型的守恒方程组进行离散化。根据以上确定的初始条件和边界条件,采用SIMPLEST思想对动量方程进行离散化,对压力方程采用全域求解,其他守恒方程采用线性迭代法求解。
2 仿真结果与分析
2.1 流速分布
当β=0°和α=45°时,流体域速度分布如图4所示。由图4(a)可见:当风速为15 m/s时,在碟式太阳能聚光器后表面会形成一个大的回流区,将使碟式太阳能聚光器后表面所受风力与前表面所受部分风力抵消。另外,在风通过碟式太阳能聚光器后表面缝隙时,流出速度有所上升,且风在碟式太阳能聚光器上下端面的速度方向沿中心向外,且下端速度大于上端速度。
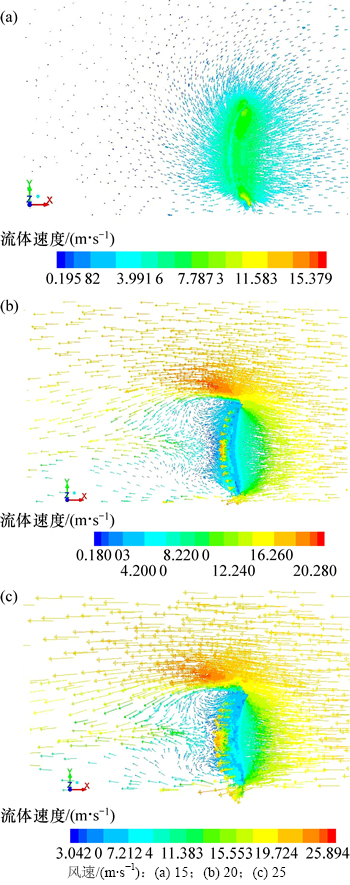
图4 β=0°和α=45°时流体域速度分布
Fig. 4 Velocity distribution of flow field when β=0° and α=45°
由图4(b)和图4(c)可见:当恒风速增大为20 m/s和25 m/s时,碟式太阳能聚光器流体域XY剖面的速度分布大致相同,数值不同。当风通过碟式太阳能聚光器流体域的缝隙时,速度增大;当风通过碟式太阳能聚光器所在区域时,碟式太阳能聚光器上下端面流体受影响而导致流体速度增加,且在碟式太阳能聚光器背面形成2个漩涡流场,并比β=0°和α=0°状态的2个漩涡流场区域更大且更清晰。
当β=45°和α=0°时,碟式太阳能聚光器流体域速度分布如图5所示。由图5可以看出:整个碟式太阳能聚光器流体域没有涡流区域出现,通过碟式太阳能聚光器端面及缝隙后流速有所增加,且碟式太阳能聚光器前表面下端流速最大,而后表面由于流场变化,形成一小片低速区,整体速度分布相似,随着碟式太阳能聚光器流体域入口风度v的增大而增大。

图5 β=45°和α=0°的流体域速度分布
Fig. 5 Velocity distribution of fluid domain when β=45° and α=0°
以上研究结果表明:当高度角β=0°时,逆恒定风来流方向的碟式太阳能聚光器表面附近将形成2个漩涡流场,且这2个涡流区域随着方位角α的增加而约为明显,而与恒定风速关系不大。当高度角β=45°时,整个碟式太阳能聚光器流体域没有涡流区域出现,碟式太阳能聚光器前表面下端流速最大,而后表面整体速度随着碟式太阳能聚光器流体域入口速度的增大而增大。
2.2 压强分布
碟式太阳能聚光器反射面压强分布云图如图6所示。由图6可知:当碟式太阳能聚光器计算域入口风速由15 m/s增大到25 m/s时,碟式太阳能聚光器反射面受到的压强也随之增大,且碟式太阳能聚光器中心区域的风压较大,而远离中心区域的风压较小,这是由于风载荷作用于碟式太阳能聚光器表面时,风向碟式太阳能聚光器的中心聚焦,而在碟式太阳能聚光器边缘出现脱离。

图6 不同风速时0-0聚光器正反射面的压强分布云图
Fig. 6 Regular reflection surface pressure distribution of 0-0 concentrator at different wind speeds
碟式太阳能聚光器在相同高度角与恒定风速下反射面压强随方位角变化的分布云图如图7所示。由图7可知:当恒定风速为15 m/s时,不同姿态下的碟式太阳能聚光器的压强分布不同,在高度角β=0°和方位角α=0°时,碟式太阳能聚光器中心区域的风压较大,而远离碟式太阳能聚光器中心区域的压强较小,这是由于风载荷作用于碟式太阳能聚光器时,风载荷向碟式太阳能聚光器中间聚集,而在碟式太阳能聚光器边缘出现脱离;聚光器在靠近来流方向的位置压强较大,而远离来流方向,压强相对较小。当改变恒定风速为20 m/s或25 m/s时,碟式太阳能聚光器在高度角β=0°时反射面压强相应增加,但其随方位角变化趋势与图7基本相似。
2.3 仿真结果分析
基于不同恒风速虚拟风洞实验下,碟式太阳能聚光器在不同高度角β和不同方位角α所受风力(包括侧力Fx、阻力Fy和升力Fz)和风力矩(包括俯仰力矩Mx、翻滚力矩My和方位力矩Mz)变化结果分别如表2和表3所示。
由表2和表3可知:当若高度角β和方位角α不变时,随着恒定风速v的增大,碟式太阳能聚光器反射面所受风压也随之增大,碟式太阳能聚光器背面的漩涡流场也越来越显著,从而导致碟式太阳能聚光器在x,y,x轴所受到的风力和风力矩也显著增加,但其保持方向不变。当风速由15 m/s变化到25 m/s时,碟式太阳能聚光器所受风力和风力矩的最大幅值至少增加了110%。当方位角α=0°,高度角由0°变化为45°
时,碟式太阳能聚光器在X方向受合力沿X轴负方向,其数值减少,而其在X方向所受转矩方向由负向变为正向,且数值增加;碟式太阳能聚光器在Y方向受到的合力沿Y轴负方向,其数值增大,在Z轴方向受到的合力沿Z轴正方向,但数值减少;碟式太阳能聚光器在Y和Z方向所受风力矩方向不变,但其数值减少。
表2 不同恒定风速下碟式太阳能聚光器所受风力
Table 2 Wind forces of dish solar concentrator at different wind conditions


图7 恒定风速15 m/s聚光器高度角为0°时不同方位角下压强分布云图
Fig. 7 Pressure distribution of condensor in different azimuth angles when v =15 m/s and β=0°
表3 不同恒定风速下碟式太阳能聚光器所受风力矩
Table 3 Wind moments of dish solar concentrator at different wind conditions

3 结论
1) 不同姿态下碟式太阳能聚光器反射面的压强分布不同,在靠近来流方向处碟式太阳能聚光器压强较大,而远离来流方向处其压强相对较小;恒定风载荷向碟式太阳能聚光器中间聚集,并在碟式太阳能聚光器边缘处存在脱离现象。
2) 不同恒风速虚拟风洞实验下碟式太阳能聚光器在不同方位角α所受风力和风力矩随碟式太阳能聚光器高度角β的变化趋势基本相似,但当风速由15 m/s增加到25 m/s时,碟式太阳能聚光器所受风力和风力矩的最大幅值至少增加了110%。
参考文献:
[1] Kalogirou S. A. Solar thermal collectors and applications[J]. Progress in Energy and Combustion Science, 2004, 30: 231-295.
[2] Sardeshpande V R, Chandak A G, Pillai I R. Procedure for thermal performance evaluation of steam generating point-focus solar concentrators[J]. Solar Energy, 2011, 85(7): 1390-1398.
[3] WU Shuangying, XIAO Lan, CAO Yiding, et al. Convection heat loss from cavity receiver in parabolic dish solar thermal power system: A review[J]. Solar energy, 2010, 84(8): 1342-1355.
[4] Reddy K S, Sendhil K N. Combined laminar natural convection and surface radiation heat transfer in a modified cavity receiver of solar parabolic dish[J]. International Journal of Thermal Science, 2008, 47(12): 1647-1657.
[5] Sendhil K N, Reddy K S. Numerical investigation of natural convection heat loss in modified cavity receiver for fuzzy focal solar dish concentrator[J]. Solar Energy, 2007, 81(7): 846-855.
[6] Zanganeh G, Bader R, Pedretti A. A solar dish concentrator based on ellipsoidal polyester membrane facets[J]. Solar Energy, 2012, 86(1): 40-47.
[7] XIAO Jun, WEI Xiudong, LU Zhenwu, et al. A review of available methods for surface shape measurement of solar concentrator in solar thermal power applications[J]. Renewable and Sustainable Energy Reviews, 2012, 16(5): 2539-2544.
[8] Hernandez N, Riveros-Rosas D, Venegas E, et al. Conical receiver for a paraboloidal concentrator with large rim angle[J]. Solar Energy, 2012; 86(4): 1053-1062.
[9] Ruelas J, Velázquez N, Cerezo J. A mathematical model to develop a Scheffler-type solar concentrator coupled with a Stirling engine[J]. Applied Energy, 2013, 101(1): 253-260.
[10] Davenport A G. Past, present and future of wind engineering[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(12/13/14/15): 1371-1380.
[11] Baker C J. Wind engineering-Past, present and future[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(9/10/11): 843-870.
[12] Solari G. The international association for wind engineering (IAWE): Progress and prospects[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(9/10/11): 813-842.
[13] Tomasini G, Cheli F. Admittance function to evaluate aerodynamic loads on vehicles:Experimental data and numerical model[J]. Journal of Fluids and Structures,2013, 38: 92-106.
[14] Pierre L M S, Kopp G A, Surry D, et al. The UWO contribution to the NIST aerodynamic database for wind loads on low buildings, Part 2: Comparison of data with wind load provisions[J]. Journal of Wind Engineering and Industrial Aerodynamics,2005, 93(1): 31-59.
[15] Sohn M H, Chang J W. Flow visualization and aerodynamic load calculation of three types of clap-fling motions in a Weis-Fogh mechanism[J]. Aerospace Science and Technology, 2007, 11(2/3): 119-129.
(编辑 赵俊)
收稿日期:2014-12-15;修回日期:2015-03-11
基金项目(Foundation item):国家留学基金资助项目(201208430262);武器装备预研重点项目(9140A2011QT4801)(Project (201208430262) supported by the China Scholarship Council Foundation; Project (9140A2011QT4801) supported by the Weapons and Equipment Pre-research Fund)
通信作者:鄂加强,博士,博士生导师,从事新能源装备性能仿真与优化等研究;E-mail:ejiaqiang@126.com