文章编号:1004-0609(2015)-11-3113-06
压电纤维复合物驱动应变性能的模拟和优化
王晓宇1,从 强1,林秀娟2,陈海燕2,王浩威1,周科朝2,张 斗2
(1. 北京空间飞行器总体设计部,北京 100094;
2. 中南大学 粉末冶金国家重点实验室,长沙 410083)
摘 要:压电纤维复合物因具有较大的驱动应变和良好的柔韧性而成为智能材料领域的研究热点之一。采用有限元法分析各结构参数对压电纤维复合物驱动应变性能的影响规律。结果表明:电场在交叉指形电极边缘发生聚集,且在此区域的电场强度约为均匀部分电场强度的4倍,因此,应用过程中压电纤维极易在电极边缘部分因应力集中而产生裂纹,从而降低复合物的驱动性能;指间距越大,复合物的驱动应变量及电场分布越接近于理想情况;采用高体积分数的压电陶瓷纤维、电极与纤维之间较小的聚合物层厚度均有利于提高智能压电纤维复合物的驱动应变性能;方形压电纤维复合物较圆形压电纤维复合物的驱动应变性能至少可提高60%。
关键词:压电纤维复合物;有限元法;压电陶瓷纤维;应变性能
中图分类号:TF111 文献标志码:A
Modeling and optimization of actuation strain property of piezoelectric fiber composites
WANG Xiao-yu1, CONG Qiang1, LIN Xiu-juan2, CHEN Hai-yan2,
WANG Hao-wei1, ZHOU Ke-chao2, ZHANG Dou2
(1. Beijing Spacecraft System Engineering, Beijing 100094, China;
2. State Key laboratory of Powder Metallurgy, Central South University, Changsha 410083, China)
Abstract: The piezoelectric fiber composites become one research focus of smart materials due to the larger strain and better stiffness than those of other piezoelectric composite. The influence of structural parameters on actuation strain property of piezoelectric composites was studied by the finite element analysis. The modeling results show that the high electric field near the electrode edge is four times larger than that in the middle of the fiber where the electric field is uniform. So in this area, the piezoelectric fiber easily cracks due to the stress concentration, which leads to the failure of composite. The electric field and the strain are close to the ideal actuator with the increase of the electrode separation. The performance of composite increases by using higher volume of the piezoelectric fiber and smaller thickness of polymer between the fiber and electrode. Compared with the circular fiber composites, the strain property of the square fiber composite is improved at least 60%.
Key words: piezoelectric fiber composites; finite element method; piezoelectric ceramic fiber; strain property
压电材料作为应用最为广泛的一类智能材料,在智能结构及控制领域得到了广泛应用,但陶瓷的脆性本质限制了其在复杂结构件上的应用[1]。由压电陶瓷纤维、聚合物基体和交叉指形电极(Interdigitated electrode,IDE)组成的压电纤维复合物中[2],交叉指形电极结构的应用有效利用了压电纤维的d33性能[3],使得复合物具有较大的驱动应变,同时也降低了极化和驱动电压。此外,该复合物可进行大幅度弯曲和扭转,很容易应用于曲面结构上[4],拓宽了压电器件的应用领域。近几年来,压电纤维复合物在能量采集[5-6]、智能结构控制[7]、稳定状态的维护及结构健康监测[8]等领域的应用显示了广阔的应用前景。
根据所用纤维形状的不同可将压电纤维复合物分为两类,分别为圆形压电纤维复合物(Active fiber composite,AFC)[1]和方形压电纤维复合物(Macro fiber composite,MFC)[9]。圆形压电纤维复合物中压电纤维与电极之间为点接触,不同部位压电纤维与电极之间的树脂粘结层厚度不同,使得同一平面内压电纤维的电场强度有所差异,进而导致应变在压电纤维中分布的差异性。方形压电纤维与电极之间为面接触,同一平面内压电纤维的电场强度基本一致,因而同一平面内的压电纤维具有相同应变。因此,纤维形状的差异使得压电纤维复合物的应变行为有所不同。BOWEN等[10]研究了以压电陶瓷片为基板的叉指状电极结构中电极指宽及指间距对其应变性能的影响。林秀娟等[11]研究电极指宽、指间距及方形纤维厚度对方形压电纤维复合物应变性能的影响。BECKERT等[12]利用有限元法对叉指状电极压电陶瓷和圆形压电纤维复合物进行研究,并对电场集中造成的材料失效风险进行了分析,对因电极指宽变化而导致的电场强度变化进行了量化,研究了纤维与电极之间聚合物层介电常数与厚度对驱动性能的影响。BELLOLI等[13]采用实验和有限元法获得的结果均显示,当单位指间距电场强度相同时,增大纤维与电极之间的接触角和指间距可有效改善圆形压电纤维复合物的驱动性能。本文作者以均匀场理论为基础,系统地分析了电极指宽度、指间距、压电陶瓷纤维厚度及体积分数等对不同结构的复合物驱动性能的影响,进而明确有效提高压电纤维复合物驱动性能的途径。
1 压电纤维复合物的有限元模拟
图1所示为压电纤维复合物结构示意图,其结构特点是:沿纤维轴向正负分支电极交叉排列,各分支电极由一对异性主电极引出,上下表面电极结构完全对称。交叉指形电极结构在纤维轴向方向具有周期性,因而每对相邻异性电极之间的压电陶瓷纤维均应具有相同的电场、应力/应变场分布状态。因此,为简化分析过程,可以采用一对相邻异性电极之间的复合物作为最小结构单元进行研究(见图2),进而反映整个复合物的宏观驱动应变性能。在该最小结构单元(RVE)中,主要的结构参数有压电纤维厚度H/2、电极宽度W/2、电极指间距P/2和聚合物层厚度L等。在此模拟分析中对结构单元施加表1所示的边界条件。
根据均匀场理论设定结构单元中压电纤维的极化方向沿Z轴方向且极化强度均匀分布。其中,有限元模拟中所使用的材料参数列于表2。
表1 结构单元所施加的位移、电压和电位移边界条件
Table 1 Boundary conditions of displacement, electrical potential and electrical displacement applied to RVE

2 结果与讨论
2.1 电场及应变在圆形和方形压电纤维复合物结构单元的分布
从图3(a)和(b)分别所示的圆形和方形压电纤维复合物结构单元的电压分布图可以看出,远离表面电极区域的电压垂直于纤维轴向方向分布,而在表面电极附近区域则成无规则分布。从图3(c)所示方形压电纤维的轴向电场分布图可以看出,表面电极边缘存在电场强度异常增大区域,此区域的电场强度值约为均匀电场部分强度的4倍,这与电极与压电材料直接接触有关。由图3(d)所示的方形纤维复合物结构单元的轴向电场线分布图可以发现,在结构单元内部远离表面电极部分电场线均沿纤维轴向方向,且电场强度也没有变化,此区域为均匀分布区域,电极下方区域电场线偏离于纤维轴向方向,为非均匀区域,同时,在电极下方存在电场强度异常小的部分区域,因电场强度异常小而导致此部分区域材料的极化强度非常弱并且对轴向的应变驱动性能的贡献几乎可以忽略不计,因此,将此部分区域称为非活跃区域。由图3(e)可以发现,在表面电极边缘存在轴向应变量的最大值,且此处的轴向应变量约为纤维内部均匀电场部分轴向应变量的4倍,由此可以推断,在此位置压电纤维极易产生应力集中而导致裂纹的出现,从而引起复合物的失效,这与PARADIES等[14]等报道的结果相互吻合。结合图3(b)和(c)可知,结构单元中电场的分布直接影响压电纤维不同区域的应变量。
2.2 压电陶瓷纤维体积分数对压电纤维复合物驱动应变性能的影响
目前,智能压电纤维复合物中普遍采用的是圆形压电纤维。这类纤维一般采用挤压成形进行制备[14],但由于制备过程中存在生坯均匀性不佳、挤压工艺条件不稳定等问题,导致纤维在直径、形状、平直度等形貌方面出现不均匀现象[15],进而引起复合物中如包封聚合物层厚度等结构参数的不均匀性,对复合物的使用及性能均产生较大影响。更重要的是,圆形纤维与交叉指形电极为点接触,在极化和使用复合物时,电场无法均匀有效地分布在压电纤维上。为解决上述问题,美国航空航天宇航局采用方形纤维替代圆形纤维后,电极与纤维的接触由点接触改为面接触,改善了电场在纤维上的分布[16],由此使得复合物驱动性能发生变化。为表征方形智能压电纤维复合物与圆形智能压电纤维复合物驱动应变性的差异,在指宽W/2为30 μm,指间距P/2为200 μm,基体厚度H/2为60 μm的条件下比较两复合物结构单元的应变量,其结果如图4所示。由图4可以看出,方形压电纤维复合物较圆形压电纤维复合物的驱动应变性能提高了至少60%,且压电纤维体积分数越小,两者之间的性能差异越大。当压电纤维体积分数为40%时,方形压电纤维复合物的驱动应变性能较圆形压电纤维复合物的提高75%。这是由于在压电纤维复合物中压电纤维为产生作用的主动相,聚合物可以起到保护纤维、传递和分散应力的作用,因而,在复合物中是从动相的作用。因而,在其他结构参数相同的条件下,圆形压电纤维复合物较方形压电纤维复合物中压电纤维所占的体积分数小,从而使得整个结构单元的应变量较方形纤维的减小。由此可以得出,使用方形压电纤维制备复合物不仅降低了制备过程中不可控因素的影响,而且可显著提高复合物的驱动性能。
表2 有限元模拟中所使用的材料参数
Table 2 Material parameters data used for finite element analysis
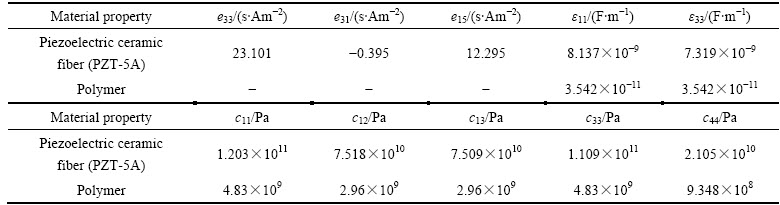

图3 有限元模拟结果
Fig. 3 Finite element results
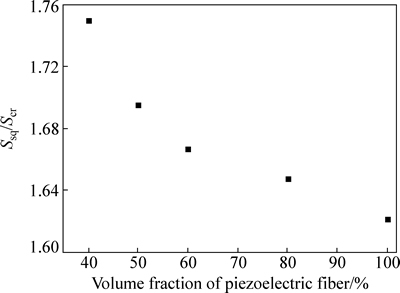
图4 Ssq/Scr与压电纤维体积分数的关系(W/2=30 μm,P/2=200 μm,H/2=60 μm)
Fig. 4 Relationship between Ssq/Scr and volume fraction of piezoelectric fiber (W/2=30 μm, P/2=200 μm, H/2=60 μm)
2.3 电极宽度对复合物驱动应变性能的影响
为了研究电极结构参数对方形和圆形压电纤维复合材料驱动性能的影响,首先考虑电极宽度对结构单元应变量的影响。设定压电纤维厚度H/2为60 μm、电极间距P/2为200 μm的条件下电极宽度W对复合物驱动应变性能的影响。从图5可以发现,电极宽度W与结构单元应变量呈现先增大后减小的趋势。对于方形压电纤维复合物,当电极宽度W为60 μm时,结构单元具有最大应变量,此时电极宽度W为压电纤维厚度H的一半,这与BOWEN等[10]的报道结果相 同[10]。图3所示为圆形压电纤维结构单元的驱动应变性能与电极宽度之间的关系。由图3也可以发现,电极宽度W与结构单元应变量也呈现先增大后减小的趋势,但结构单元的最大应变量出现在电极宽度为160 mm时。对比图5中结构单元的单位平均应变量可以得知,圆形压电纤维复合物较方形压电纤维复合物的驱动应变能力对电极指宽的变化更为敏感。
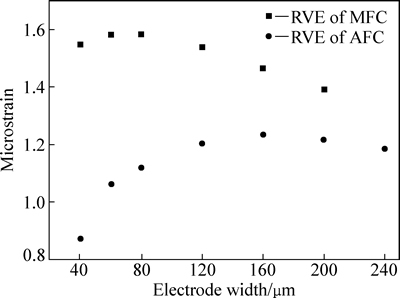
图5 电极宽度W与结构单元应变量之间的关系(H/2=60 μm)
Fig. 5 Relationship between electrode width W and structural strain response of RVE (H/2=60 μm)
2.4 指间距对复合物驱动应变性能的影响
图6所示为压电纤维厚度H/2为60 μm,电极宽度W/2为30 μm,ΔU/(P/2)=1 kV/mm的条件下,方形和圆形压电纤维复合物的结构单元中指间距P变化对复合物驱动应变性能的影响。由图6可以发现,随着指间距的增大,结构单元的应变量增大。这是由于随着指间距的增大,不均匀电场区域和非活跃区域所占的体积分数逐渐减小。同时,由图6也可以发现,圆形压电纤维复合物较方形压电纤维复合物对因电极指间距变化而引起的驱动应变性能的变化更为敏感。选取指间距较大的压电纤维复合物越易获得较大的驱动应变,但随着指间距的增大,所需要的极化电压和驱动电压会相应增大,同时,也提高了极化和使用过程中对设备的要求。
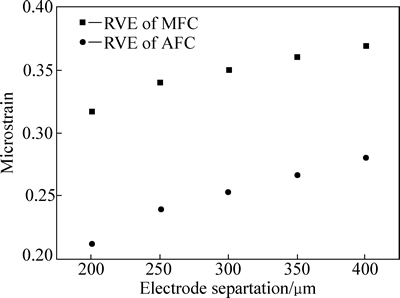
图6 电极指间距S与结构单元应变量关系(W/2=30 μm,H/2=60 μm)
Fig. 6 Relationship between electrode separation S and structural strain response of RVE (W/2=30 μm, H/2=60 μm)
2.5 聚合物层厚度对复合物驱动应变性能的影响
图7所示为聚合物层厚度与结构单元应变量关系。从图7中可以看出,压电陶瓷与电极之间即使存在厚度非常小的聚合物层也会对复合物的性能产生极大的不利影响。且聚合物层厚度较小时对复合物驱动应变性能的影响极为显著,当聚合物层达到一定厚度后,复合物的驱动应变性能变化不再明显。这是由于聚合物的介电常数较压电陶瓷约低2个数量级,在整个结构中聚合物相当于电容器从而分担了通过电极施加给压电纤维的电压,使得实际施加在压电纤维上的电压非常小,这就使得整体压电纤维复合物的性能受到极大程度的影响。因此,若使压电陶瓷纤维上仍具有较强的电场强度,一方面可以通过增大极化和驱动电压来实现,但这同时会使得电极边缘电场强度异常增大区域容易产生介质击穿和因应力集中而引起纤维断裂;另一方面,增大聚合物的介电常数或尽可能的减小电极与压电纤维之间的聚合物层厚度都可以在一定程度上改善压电纤维复合物的性能。
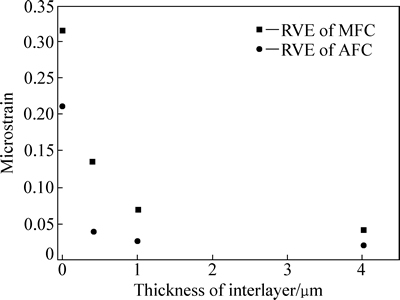
图7 聚合物层厚度与结构单元应变量关系(W/2=30 μm,H/2=60 μm)
Fig. 7 Relationship between interlayer thickness and structural strain response of RVE (W/2=30 μm, H/2=60 μm)
3 结论
1) 智能压电纤维复合物中交叉指形电极结构的引入能够有效利用压电纤维优异的d33性能,但同时也使纤维内部存在电场强度非常小,几乎处于不工作状态的“非活跃区”和电场强度不均匀且方向偏离于纤维轴向的不均匀电场区域。
2) 对不同结构的压电纤维复合物进行有限元模拟,结果表明:交叉指形电极边缘区域电场强度约为均匀部分电场强度的4倍。在此区域,压电纤维易产生应力集中而导致裂纹产生;指间距越大,复合物的驱动应变量及电场分布越接近于理想情况。
3) 采用高体积分数的压电陶瓷纤维、电极与纤维之间较小的聚合物层厚度均有利于提高智能压电纤维复合物的驱动应变性能。
4) 方形压电纤维复合物较圆形压电纤维复合物的应变性能至少提高60%。
REFERENCES
[1] BENT A A. Active fiber composites for structural actuation[D]. Massachusetts: Massachusetts Institute of Technology, 1997.
[2] BENT A A, HAGOOD N W. Piezoelectric fiber composites with interdigitated electrodes[J]. Journal of Intelligent Material Systems and Structures, 1997, 8(11): 903-919.
[3] BENT A A, HAGOOD N W. Improved performance in piezoelectric fiber composites using interdigitated electrodes[C]. Smart Structures and Materials. San Diego: SPIE, 1995: 196-212.
[4] PARADIES R, CIRESA P. Active wing design with integrated flight control using piezoelectric macro fiber composites[J]. Proceeding of SPIE, Smart Materials and Structures. San Diege: Smart Materials, 2009, 18(3): 1-9.
[5] SONG H J, CHOI Y T, PUREKAR A S, WERELEY N M. Performance evaluation of multi-tier energy harvesters using macro-fiber composite patches[J]. Journal of Intelligent Material Systems and Structures, 2009, 20(17): 2077-2088.
[6] YANG Yao-wen, LI Hua-tang, LI Hong-yun. Vibration energy harvesting using macro-fiber composites[J]. Smart Materials and Structures, 2009, 18(11): 1-8.
[7] HOU Zhi-wei, CHEN Ren-wen, XU Zhi-wei, LIU Qiang. Application of macro-fiber composite to structural vibration suppression[J]. Journal of Vibration, Measurement and Diagnosis, 2010, 30(1): 51-54.
[8] LIN Cui, YU Liu, SOH C K. Health monitoring of cylindrical structures using torsional wave generated by piezoelectric macro-fiber composite[C]. Proceeding of SPIE, Health Monitoring of Structural and Biological Systems. San Diego: SPIE, 2011: 1-9.
[9] KOVALOVS A, BARKANOV E, GLUHIHS S. Active control of structures using macro-fiber composite[C]. Journal of Physics:Conference Series. San Diego: SPIE, 2007: 12-34.
[10] BOWEN C, NELSON L, STEVENS R, CAIN M, STEWART M. Optimisation of interdigitated electrodes for piezoelectric actuators and active fibre composites[J]. Journal of Electroceramics, 2006, 16(4): 263-269.
[11] 林秀娟, 张 斗, 张晓泳, 李志友,周科朝. 基于有限元法压电纤维复合物结构的模拟优化[J]. 中国有色金属学报, 2012, 22(6): 1747-1753.
LIN Xiu-juan, ZHANG Dou, ZHANG Xiao-yong, LI Zhi-you, ZHOU Ke-chao. Modeling and optimization of piezoelectric fiber composites based on finite element method[J]. The Chinese Journal of Nonferrous Metals, 2012, 22(6): 1747-1753.
[12] BECKERT W, KREHERE W. Modelling piezoelectric modules with interdigitated electrode structures[J]. Computational Materials Science, 2003, 26: 36-45.
[13] BELLOLI A, CASTELLI B, KORNMANN X, HUBER C, ERMANNI P. Modeling and characterization of active fiber composites[C]. Smart Structures and Materials 2004: Smart Structures and Integrated Systems. Belliham: SPIE, 2004: 78-88.
[14] PARADIES R, MELNYKOWYCZ M M. State of stress in piezoelectric elements with interdigitated electrodes[J]. Journal of Electroceramics, 2010, 24(3): 1-8.
[15] KORNMANN X, HUBER C. Microstructure and mechanical properties of PZT fibres[J]. Journal of the European Ceramic Society, 2004, 24(7): 1987-1991.
[16] WILKIE W K, BRYANT R G, HIGH J W, FOX R L, HELLBAUM R F, JALINK A, LITTLE B D, MIRICKL P H. Low-cost piezocomposite actuator for structural control applications[C]. Smart Structures and Materials 2000. Industrial and Commercial Applications of Smart Structures Technologies. Newport Beach: SPIE, 2000: 323-334.
(编辑 李艳红)
基金项目:国家“十二五”装备预先研究项目(51320030101);国防基础科研项目(A1420133028);高等学校博士学科点专项科研基金(20110162110044);国家自然科学基金资助项目(51072235)
收稿日期:2014-04-24;修订日期:2015-09-11
通信作者:张 斗,教授,博士;电话:0731-88877196;E-mail:dzhang@csu.edu.cn