Electronic structure of Au-Cu alloys

YU Fang-xin(Óà·½ÐÂ), XIE You-qing(лÓÓÇä), NIE Yao-zhuang(Äôҫׯ),

LI Xiao-bo(ÀîС²¨), PENG Hong-jian(Åíºì¼ü), TAO Hui-jin(ÌÕ»Ô½õ)

(School of Materials Science and Engineering, Central South University, Changsha 410083, China)

Abstract: By studying the correlativity between energy, volume and electronic structure of characteristic crystals and bound conditions of OA theory, the potential energy function, atomic volume interactive function and electronic structure of Au-Cu alloys have been determined. Then following the general Vegard¬ðs law in characteristic theory, the electronic structure and properties of disordered continue solid solution and three ordered alloys with the maximum ordering degree are calculated. It is found that the non-bonding electrons and near-free electrons in outer shell will transform to covalent electrons during alloying. By analyzing the variation of electronic structure and cohesion of ordering and disordered alloys, the transformation of order-disorder transition Au-Cu alloy has been studied.

Key words: CC theory; electronic structure; Au-Cu alloy; ordering transformation CLC number: TG111

Document code: A

1 INTRODUCTION

As a traditional alloy, Au-Cu system is extensively applied in catalysis, electronic industry and biological material field. Recently, some new functions of the alloy are found in nano-crystal and thin film materials^[1-4]. It is well known that there exist transformations of order-disorder transition in Au-Cu system. Comprehensive theoretical and experimental studies have been contributed to these transformations^[5-8]. Most of these studies are focused on the thermodynamic properties and dynamic process. The present paper attempts to explore the intrinsic causes of order-disorder transitions by studying the interactions of the constituents and the correlativity among energy, volume and electronic structure of characteristic crystals in the alloy.

The potential energy and volume interaction functions of Au-Cu alloy are established according to CC theory, and then the electronic structures and physic properties of ordering and disordering structures in the alloy are calculated. As a consequence the intrinsic causes of order-disorder transformation in the alloy are analyzed.

2 INTERACTION FUNCTIONS OF POTENTIAL ENERGY AND VOLUME IN DISORDERED ALLOY

Characteristic crystals(CC) theory^[9-14]are developed from central atoms model^[15]. According to the central atoms model, even atoms of the same component in solid solution alloys may have different electronic structures and properties due to variant environment, i.e. variant coordination number and coordinate atoms, and separate into different characteristic atoms. For alloys of two components, there are characteristic atoms: A₀¡­Ai¡­AI, B₀¡­Bi¡­BI where i is the number of B atoms in the nearest neighboring shell, and I is the coordination number. Characteristic crystal consists of one certain characteristic atom and has the same crystal structure with the alloy. Ref.[9] derived the relationship between i and atom¬ðs potential energy and volume of characteristic crystals. Table 1 lists the interaction functions of potential energy and volume in disordered alloy.

3 POTENTIAL ENERGY FUNCTIONS OF Au-Cu ALLOYS

The parameters and E^Au₀ and E^Cu₀are, respectively, molar potential energies of characteristic crystal with primary states. Because the Au-Cu alloys have the same type of fcc crystal structure as that of pure elements Au and Cu, the characteristic crystals with primary states ¦×^Au₀ and ¦×^Cu_I are respectively pure elements with atomic states ¦×⁰_Au and ¦×⁰_Cu. From this, it can be known that E^Au₀=E⁰_Au, E^Cu_I=E_Cu where E_Au and E_Cu are equal to negative value of cohesive energies of pure metal Au and Cu respectively. The parameters E^Au_I and E^Cu₀ are, respectively, molar potential energies of characteristic crystal with terminal states ¦×^Au_I and ¦×^Cu₀. The values of E^Au_I and E^Cu₀ in the nine potential interaction functions can be, in principle, determined by experimental values of heat of formation of only two alloys.

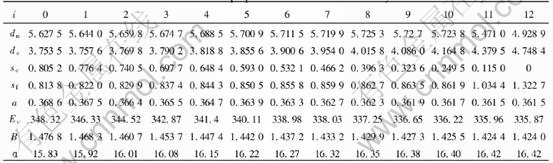
Once the values of parameters E^Au₀, E^Au_I, E^Cu₀ and E^Cu_I are known, the cohesive energies of characteristic crystal can be calculated from the corresponding potential functions of components where the subscript i is the number of Cu atoms in the nearest neighboring configuration and can change from 0 to I. I is the coordination number and is equal to 12 for Au-Cu alloys. Table 2 lists the cohesive energies of Au and Cu characteristic in Au-Cu alloys.

Table 1 Interaction functions of potential energy(Q=E) and volume(Q=V) of disordered binary solid solution

Table 2 Cohesive energies of Au and Cu characteristic crystals in Au-Cu alloys(kJ/mol)

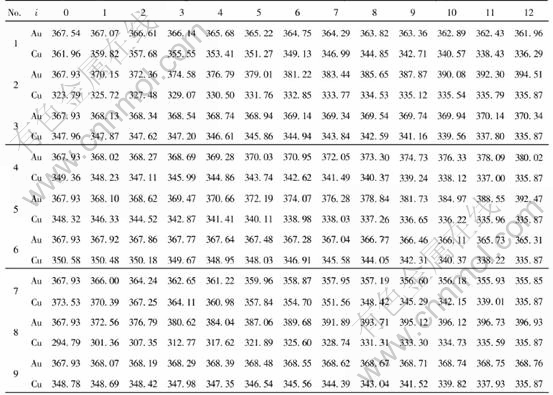
_{4 VOLUME INTERACTION FUNCTIONS OF Au-Cu ALLOYS}

_{If V is used instead of E, nine potential energy functions in Table 1 become nine V-functions of CC theory. Parameters V}^Au_{0 and V^CuI are respectively the atom volumes with primary state of Au and Cu characteristic crystals. Because the Au-Cu alloys have the same type of fcc crystal structure as that of pure elements Au and Cu, the characteristic crystals with primary states ¦×}^Au_{0 and ¦×^CuI are respectively pure elements with atomic states ¦×}⁰_{Au and ¦×}⁰_{Cu. From this it can be known that, V}^Au_0=V⁰_{Au, V^CuI=V}⁰_{Cu. The parameters, V^AuI and V}^Cu_{0, are respectively atomic volumes of terminal characteristic crystals ¦×^AuI and ¦×}^Cu_{0 of components Au and Cu. The values of the nine V-function can be, in principle, determined by experimental values of lattice constants of only two alloys.}

_{Once the values of V}^Au_{0, V^AuI, V^CuI and V}^Cu_{0 of each V-function are known, the lattice constants a^Aui and V^Cui of characteristic crystal, obtained by equation(a=(4V)}^1/3_{), can be calculated from the atomic volume equations of components corresponding to each V-function of the Au-Cu alloys. The results are listed in Table 3.}

_{5 ELECTRONIC STRUCTURE OF CHARACTERISTIC CRYSTAL IN Au-Cu ALLOYS}

Obtaining the cohesive energies and lattice constants of characteristic crystals in alloys, the electronic structure can be calculated according to OA theory[16, 17]. In OA theory, the electronic structures of pure metals is described by the quasi-electron-occupation(QEO) number of the one-atom state ¦×a which is made up of some basic atom states ¦Õk:

_{The atoms are condensed into the crystal by metallic bond, which is a mixing bond of un-saturated covalent electronic bond, free electronic bond and magnetic electronic bond. Therefore, there exist covalent electrons(nc), near-free electrons(nf), magnetic electrons(nm), and non-bond electrons(nn) in the metals. The potential function with many-atom interactions in solid relates the atomic state to the cohesive energy and lattice constant of the crystal. For a given crystal with a certain electronic structure, a set of more complete data about cohesive energy, lattice constants, bulk modulus, elastic modulus, shear}

_{Table 3 Lattice constants of Au and Cu characteristic crystals in Au-Cu alloys(nm)}

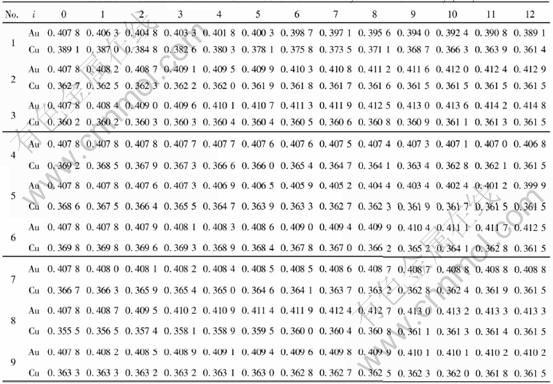
_{modulus, Poisson¬ðs ratio, specific heat and thermal expansion coefficient as a function of temperature can be obtained. The electronic structure and properties of Au and Cu characteristic crystals in Au-Cu alloys obtained by OA theory are listed in Tables 4 and 5, in which sc and sf refer respectively to covalent electrons and near-free electrons in the s orbit; dc and dn, refer covalent electrons and non-bond electrons in the d orbit, respectively; Ec, cohesive energy(kJ/mol); a, lattice constant equal to (4V)}^1/3_{, nm; B, bulk modulus, 10}¹¹_N¡¤m^-2_{; ¦Á, linear thermal expansion coefficient at 293K, 10}^-6_{. Some understanding can be obtained from these results.}

_{Electronic structure, cohesive energy, lattice constant and physical properties of each characteristic crystal are correlative. Therefore, the E-function and V-function for a given alloy system must be correlative.}

_{Comparing cohesive energies of Au and Cu characteristic crystals in Tables 4 and 5 with those in Table 2, it can be seen that the correct E-function of Au-Cu alloys is the 5th function in Table 1, namely}

^{Comparing lattice constants of Au and Cu characteristic crystals in Tables 4 and 5 with those in Table 3, it can be known that the correct V-function of Au-Cu system is the 5th function in Table 1, namely}

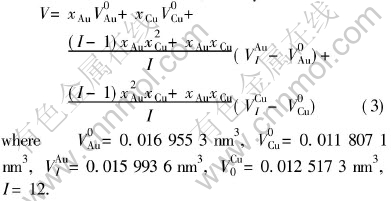
^{As to Au(Cu) characteristic atoms, atomic potential energies rise as the numbers of Cu(Au) atoms in the nearest neighboring shell increase, which are essentially due to the increase of d}_c ^{covalent electrons in the Au(Cu) characteristic atoms with increase in the i value. Such changes lead to the tendency to form ordering structure for Au-Cu alloys.}

^{6 ELECTRONIC STRUCTURE AND PROPERTIES OF DISORDERED Au-Cu ALLOYS}

^{According to CC theory, no matter what imaginable variation the atomic arrangement in the}

^{Table 4 Electronic structure and properties of Au characteristic crystals in Au-Cu alloys}

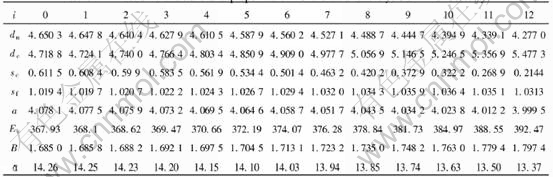
^{Table 5 Electronic structure and properties of Cu characteristic crystals in Au-Cu alloys}

 ^{lattice occurs, the relative concentrations of characteristic crystals would change, but their electronic structure and properties of characteristic crystals will not. Therefore, once the electronic structure and properties of characteristic crystals have been determined, no matter what the designed atomic arrangement in the lattice is, the electronic structure and properties of the alloy can be predicted. For disordered alloys, the concentration of characteristic crystals can be calculated by Eqn.(2). Substituting the electronic structure, cohesive energies and atomic volumes of characteristic crystals in Tables 4 and 5 into Eqn.(1), the average electronic structure, cohesive energies and lattice constants of disordered Au-Cu alloys and their components can be obtained.}

^{The common equations for calculating average electronic structure and properties of components Au and Cu are, respectively}

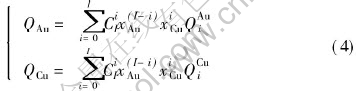
_{The electronic structure parameters, cohesive energies(kJ/mol) and lattice constants(nm) of disordered Au-Cu alloys and their components are listed in Table 6.}

_{7 ELECTRONIC STRUCTURE AND PROPERTIES OF ORDERED Au-Cu ALLOYS AND INTERMETALLIC COMPOUND}

_{The Au-Cu system is a typic ordering alloy system. According to CC theory, the transformation from a disordered state to ordered state is the degenerative process of characteristic atom. In Au3Cu-L12, there just exist the characteristic atoms 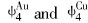, therefore, the electronic structure of the compound is combined by the characteristic atoms in states 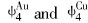, which is}

_{0.75[Xe](5dn)}^4.61_(5dc)^4.80_(6sc)^0.56_(6sf)^1.02₊

_{0.25[Ar](3dn)}^4.93_(3dc)^4.75_(4sc)⁰_(4sf)^1.32

_{Just the same, the electronic structures of compound AuCu-L10 and Au-Cu3-L12 are}

_0.5[Xe](5dn)^4.49_(5dc)^5.06_(6sc)^0.42_(6sf)^1.03₊

_0.5[Ar](3dn)^5.69_(3dc)^3.82_(4sc)^0.64_(4sf)^0.84

_and

_{0.25[Xe](5dn)}^4.28_(5dc)^5.48_(6sc)^0.21_(6sf)^1.03₊

_{0.75[Ar](3dn)}^5.73_(3dc)^4.02_(4sc)^0.40_(4sf)^0.86

_{respectively.}

_{For the ordered alloys of non-stoichometry, the concentration of the characteristic atoms can be}

_{Table 6 Average electronics and properties of disordered Au-Cu alloys and their components}

^{calculated by statistics method. As to fcc AB-L1}₀ ^{type of ordered alloys, the relationship expressions between the concentrations of the characteristic atoms, compositions of the elements and ordering degrees of alloys are}

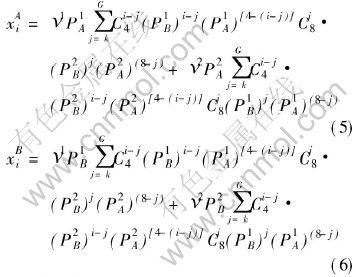
_where ¦Í¹_{, ¦Í}² _{represent the site fraction of sublattice ¢ñ, ¢ò, respectively, ¦Í}¹_=¦Í²_{=1/2; k and G take their values according to}

_P¹_{A, P}¹_{B, P}²_{A, P}²_{B are the probabilities of A and B atom occupying the first and second sublattice, which can be calculated by the equations:}

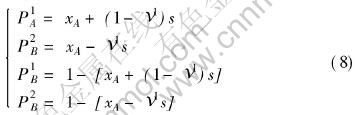
_{where s is the ordering degree, which is defined as}

_{The maximum ordering degree smax is determined from composition xA of alloys.}

_{For the stoichiometric alloy, due to, P}¹_{A=1, smax^=1.}

For the alloys with xA¡´¦Í1 due to P2A=0, smax=xA/¦Í1.

_{For the alloys with xA¡´¦Í}¹_{, due to P}¹_{A=0, smax^=(1-xA)/(1-¦Í¹).}

As to fcc A3B-L12 and AB3-L12 type of ordered alloys, there are also equations to calculate the concentrations of characteristic crystals[12].

_{The average electronic structure and properties of ordered alloys in such types as Au3Cu-L12, AuCu-L10 and AuCu3-L12 with maximum ordering degree as a function of composition are respectively listed in Tables 7, 8 and 9.}

_{Fig.1 illustrates the varying tendencies of}

_{Table 7 Average electronic structure and properties of ordered Au3Cu alloys and their components}

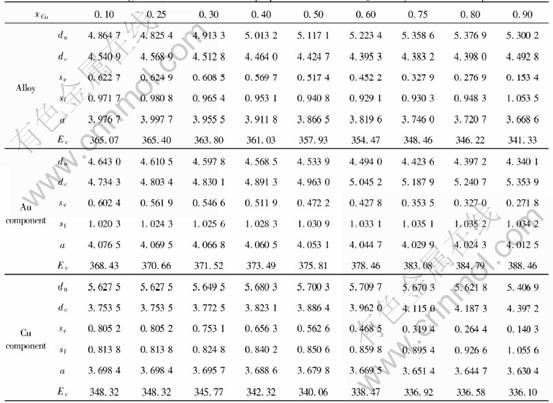
^{Table 8 Average electronic structure and properties of ordered AuCu alloys and their components}

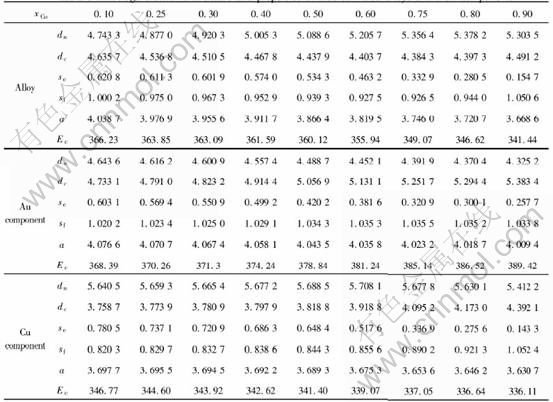
^{Table 9 Average electronic structure and properties of ordered AuCu}₃ ^{alloys and their components}

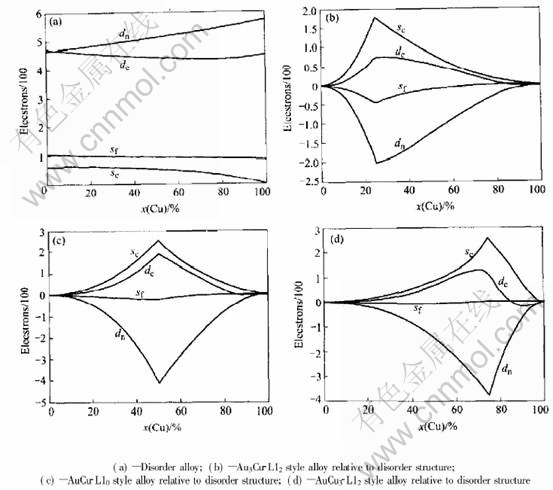
^{Fig.1 Electronic structure of Au-Cu alloys}

^{electronic structure parameters of Au}₃^Cu-L1₂^{, AuCu-L1}₀^{, AuCu}₃^-L1₂ ^{type ordered alloys relative to disorder alloy.}

^{8 ANALYZING OF ELECTRONIC STRUCTURE AND ENERGIES DURING TRANSFORMATION BETWEEN ORDERED-DISORDERED ALLOYS}

^{From Fig.1, it can be found that the electronic structure of alloys varies with the transformation of disorder-order transition. Some non-bond electrons and near-free electrons become covalent electrons when the disorder alloys transform to order alloys. At the composition of stoichiometry, there are most electrons to turn to covalent electrons from non-bond and near-free electrons. It¬ðs known that the contributions to cohesive energy are different for covalent, non-bond and near-free electron. It can be predicted that there is difference in the cohesive energies of alloys with order and disorder structure. From Tables 7, 8 and 9, it can be seen that, for the alloy of 25%Cu(mole fraction), the cohesive energy of disorder alloy is 363.16kJ/mol, but the cohesive energy of alloy with the structure of Au}₃^Cu-L1₂ ^{is 365.40kJ/mol; for the alloy of 50%Cu(mole fraction), the cohesive energy of disorder alloy is 356.91kJ/mol, but the cohesive energy of alloy with the structure of AuCu-L1}₀ ^{is 360.12kJ/mol; for the alloy of 75%Cu(mole fraction), the cohesive energy of disorder alloy is 348.16kJ/mol, but the cohesive energy of alloy with the structure of AuCu}₃^-L1₂ ^{is 351.06kJ/mol. The differences between disorder and order alloy are -2.24, -3.21, and -2.9kJ/mol respectively. This indicates that the order alloys are in lower energy states than disorder alloy, i.e. there exists ordering trend in Au-Cu system.}

^{9 CONCLUSIONS}

^{1) The energy function and volume function of Au-Cu system have been chosen by studying the atomic states, energies and volumes correlatively.}

^{2) The electronic structure, cohesive energies, lattice constants, bulk modulus, and thermal expansion coefficients of characteristic crystals in the Au-Cu system have been determined.}

^{3) The variations of electronic structure, cohesive energies and lattice constants of disordered Au-Cu alloys and three ordering alloys with the maximum ordering degree as a function of composition have been calculated.}

^{4) The transformation of order-disorder transition in the Au-Cu system has been studied based on the analysis of electronic structure and cohesive energies of the order and disorder structures in the system.}

^REFERENCES

^{[1]De Goutam, Rao C N R. Two-dimensional Au and Au-Cu alloy nanocrystals with orientation in (111) plane embedded in glassy silica films [J]. Journal of Physical Chemistry B, 2003(11): 13597-13600.}

^{[2]Battezzati L, Baricco M, Belotti M, et al. Microstructure and thermal stability of ¡®Nanocrystalline¡¯ electrodeposited Au-Cu alloys [J]. Materials Science Forum,2001, 360: 253-260.}

^{[3]Zhai H R, Zhou S M, Huang H B, et al. Magneto-optical Kerr effect of Fe/Au-Cu and Fe/Al-Cu bilayers [J]. Journal of Magnetism and Magnetic Materials, 1992, 2: 1015-1016.}

^{[4]Sakurai Makoto, Shinjo Teruya. Magneto-optical properties and magnetic anisotropies for Au/Cu/Au/Co and Cu/Au/Cu/Co multilayers [J]. Journal of Applied Physics, 1993, 1: 6840-6846.}

^{[5]Darby S, Mortimer-Jones T V. Theoretical study of Cu-Au nanoalloy clusters using a genetic algorithm [J]. Journal of Chemical Physics, 2002, 22: 1536 -1550.}

^{[6]Han X J, Chen M, Guo Z Y. Thermophysical properties of undercooled liquid Au-Cu alloys from molecular dynamics simulations [J]. Journal of Physics Condensed Matter, 2004, 16(6): 705-713.}

^{[7]Bykov A, Pastukhov E. Calorimetric study of alloy formation in Au-Cu and Au-In systems [J]. Journal of Thermal Analysis and Calorimetry, 2000, 60(3): 845-850.}

^{[8]Sundman B, Fries S G, Oates W A. CALPHAD assessment of the Au-Cu system using the cluster variation method [J]. Zeitschrift fuer Metallkunde/Materials Research and Advanced Techniques, 1999, 90(4): 267-273.}

^{[9]XIE You-qing. Atomic energies and Gibbs energy functions of Ag-Cu alloys [J]. Science in China Ser E, 1998, 41(2): 146-156.}

^{[10]XIE You-qing. Atomic volumes and volume functions for Ag-Cu alloys [J]. Science in China Ser E, 1998, 41(2): 157-168.}

^{[11]XIE You-qing, ZHANG Xiao-dong. Phase diagram and thermoldynamic properties of Ag-Cu alloys [J]. Science in China Ser E, 1998, 41(4): 348-356.}

^{[12]PENG Kun. The Systematic Study of The Electronic Structure and Properties of Ti-Al System [D]. Changsha: School of Materials Science and Engineering, Central South University, 2001.}

^{[13]Xie Y Q, Peng K, Liu X B. Influence of xTi/xAl on atomic states, lattice constans and potential-energy planes of ordered Fcc TiAl-type alloys [J]. Physica B, 2004, 344: 5-20.}

^{[14]XIE You-qing, PENG Kun, LIU Xin-bi. Monoatom control designing of disordered hcp TixAl}_(1-x) ^{alloy [J]. The Chinese Journal of Nonferrous Metals, 2002, 12(4): 205-212.}

^{[15]Lupis C H P. Chemical Thermodynamics of Materials [M]. North-Holland: Amsterdam, 1983. 438-469.}

^{[16]XIE You-qing. A new potential function with many-atom interactions in solid [J]. Science in China Ser A, 1992, 8: 880-890.}

^{[17]Xie Y Q. Electronic structure and properties of pure iron [J]. Acta Metall Mater, 1994, 42(11): 3705-3715.}

^{(Edited by PENG Chao-qun)}

Foundation item: Project(50271085) supported by the National Natural Science Foundation of China

Received date: 2004-04-09; Accepted date: 2004-07-23

Correspondence: YU Fang-Xin, PhD candidate; Tel: +86-731-8879287; E-mail: yfx11@263.net