文章编号:1004-0609(2008)06-1020-07
镁合金ZK60的三维加工图及失稳分析
刘 娟,崔振山,李从心
(上海交通大学 模具CAD国家工程研究中心,上海 200030)
摘 要:在PRASAD提出的二维加工图的基础上,建立包含应变的三维加工图,经分析得到适合镁合金ZK60的失稳判据,讨论并解决了三维加工图绘制中的关键技术。在Gleeble-1500热模拟机上对镁合金ZK60进行了热压缩实验,研究了200~360 ℃和0.01~5 /s条件下的热变形行为。该加工图的结果显示一个非失稳、功率耗散峰值区:温度为300~360 ℃、应变速率为0.01~0.1 /s,功率耗散平均值为35%,此区为适合的加工区。
关键词:ZK60;三维加工图;动态材料模型;功率耗散系数;流变失稳
中图分类号:TG 113.26 文献标识码:A
Three-dimensional processing maps and flow instability of
magnesium alloys ZK60
LIU Juan, CUI Zhen-shan, LI Cong-xin
(National Die and Mold CAD Engineering Research Center, Shanghai Jiao Tong University, Shanghai 200030, China)
Abstract:Based on the processing map proposed by PRASAD, the three-dimensional processing maps including strain were built and the favorite instability criterion was studied and the key technologies in plotting the three-dimensional processing maps were discussed. The Gleeble-1500 thermomechanical simulation tests of magnesium alloy ZK60 were conducted. The hot deformation behaviors in the temperature range of 200-360 ℃ and strain rate range of 0.01-5 /s were studied. The three-dimension processing maps show that the most favorite deformation domain is the temperature range of 300-360 ℃ and the strain rate range of 0.01-0.1 /s, with a peak efficiency of power dissipation of about 28%.
Key words:ZK60; 3-D processing map; dynamic material model; power dissipation efficiency; flow instability
FROST和ASHBY[1]用ASHBY图的形式描绘了材料对加工工艺参数的反应,由于此图基于蠕变机制,只适用于低变形速率的情况,一般的塑性加工在高几个数量级的应变速率上进行,因而会发生Ashby图不能预测的变形机制。RAJ[2]利用原子方法与基本参数相结合,绘制了纯金属和稀合金化金属的加工图。可是难于获得商用合金化金属的原子数据,以至于无法绘制商用合金化金属的加工图。而以动态材料模型(Dynamic material model, DDM)为基础的加工图弥补了前面两者的不足。加工图是金属加工工艺设计和优化的一种强有力工具,不仅描述了确定性区域中某种特定微观组织的变形机制,而且还描绘了加工过程中应该避免的不稳定性流变区域,并且还可获得优化的可加工温度和应变速率,已经在大约200多种合金中得到应用[3-6]。在国内,应用加工图研究合金的热变形行为仅限于高温合金、钛合金、镁合金等少数几种金属[7-9]。目前国内外对加工图的研究仅限于应用加工图来优化制定工艺,未见对加工图的完善和推广。
PRASAD[6]指出应变量对热加工图的影响不大,认为不同应变量下热加工图的形状相似,因此传统的加工图表示了一定应变下,应变速率和温度所构成的二维空间的功率耗散值和失稳分布。对于具有应变软化的金属,在变形的开始阶段,流变应力随应变的增加而不断的增加,应力达到某一峰值后开始下降,当动态软化足以抵消因变形引起的加工硬化后,流变应力开始趋于一恒定值,因此应力随应变发生较大变化。研究发现,对于这种类型的材料,功率耗散图和失稳图随应变的增加有较大的变化。因此,本文作者提出了包含应变、应变速率和温度的三维加工图,从中可以清楚地确定金属的可加工区域,对工艺设计具有实际的指导意义。
1 加工图的建模基础
基于DMM的加工图是应变速率和温度空间中的功率耗散图与失稳图的叠加图。在恒定的温度和应变条件下,热变形中的金属材料的动态本构方程为

式中 K是一个常数,m是应变速率敏感性指数,表示为

材料在热加工过程中单位体积内所吸收的总功率可以用两个互补函数的和来表示:
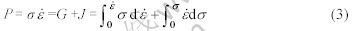
前者积分称为G(耗散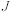 是与材料变形过程中组织变化有关的功率消耗,所以
是与材料变形过程中组织变化有关的功率消耗,所以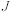 的变化也代表了微观组织的变化。在给定应变和温度条件下,
的变化也代表了微观组织的变化。在给定应变和温度条件下,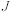 与G的变化率就构成了应变率敏感指数的定义式,如下所示:
与G的变化率就构成了应变率敏感指数的定义式,如下所示:

将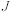 其与理想线性耗散因子Jmax进行标准化后得到一个无量纲参数-功率耗散系数
其与理想线性耗散因子Jmax进行标准化后得到一个无量纲参数-功率耗散系数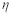 ,定义为
,定义为

参数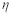 本质地描述了加工件在施加的温度和应变范围内的微观变形机制。功率耗散系数
本质地描述了加工件在施加的温度和应变范围内的微观变形机制。功率耗散系数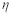 的等值线组成功率耗散图。功率耗散图代表材料显微组织改变时功率的耗散。
的等值线组成功率耗散图。功率耗散图代表材料显微组织改变时功率的耗散。
动态材料模型的连续失稳判据是基于ZIEGLER[10]提出的塑性流变变为不稳定的条件,这一判据是根据不可逆热力学极值原理建立的:

式中 D是耗散函数,是材料本构变形行为具有的特征,D用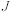 代替时,式(6)能写为
代替时,式(6)能写为

把参数 作为温度和应变速率的函数作图,在负值区域会出现流变失稳,这样的图被称为失稳图。
作为温度和应变速率的函数作图,在负值区域会出现流变失稳,这样的图被称为失稳图。
根据加工图可以确定加工的安全区和流变失稳区。安全区在微观机制上与动态再结晶、动态回复和超塑性有关。在材料的安全加工区,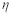 越大,表明材料内在可加工性越好。
越大,表明材料内在可加工性越好。
2 实验和分析
镁合金由于具有密排六方晶体结构,在室温下塑性变形能力差,高温下晶粒粗大且易发生表面氧化,对应变速率敏感,加工时的变形量不能很大,在塑性变形时要严格控制温度、应变速率和应变,因而被认为是难以塑性变形的金属材料,该合金的热变形规律及热加工工艺一直为人们所关注。以镁合金ZK60(Mg-6%Zn-0.5%Zr)为例,试样直径10 mm,长度为17 mm。在Gleeble-1500热模拟实验机上进行等温压缩变形,其不同温度和应变速率下的应力-应变曲线如图1所示[11]。
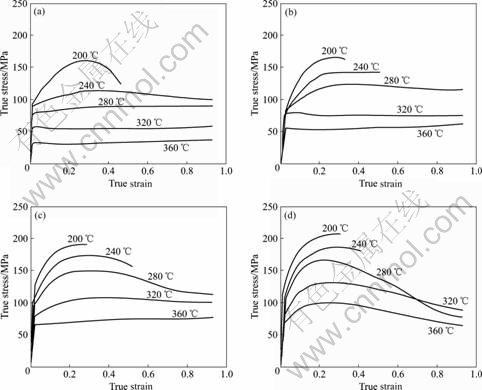
图1 镁合金ZK60真应力-真应变曲线
Fig.1 True stress—ture strain curves of magnesium alloy ZK60: (a) 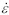 =0.01 /s; (b)
=0.01 /s; (b) 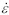 =0.1 /s; (c)
=0.1 /s; (c) 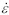 =1 /s; (d)
=1 /s; (d) 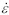 =5 /s
=5 /s
由流变应力曲线知:在低温时即在温度为200 ℃或高应变速率温度稍高时即温度为240 ℃且应变速率大于等于0.1 /s时,镁合金ZK60发生了断裂,因此这些曲线只有断裂前的一部分。在温度较高时,流变应力曲线可分为两类。一类是具有明显的硬化部分的曲线,在高应变速率即应变速率为5 /s或在温度较低应变速率较高时,即温度为280 ℃时应变速率为1 /s,这时随应变的增加,应力先增加达到峰值,然后逐渐减少,趋于稳态,流变应力随应变发生了较大的变化。另一类是在温度较高和应变速率较低时,随应变的增加,由于发生动态再结晶,加工硬化和动态再结晶引起的软化作用基本达到平衡时,流变应力近似为恒定值。由于镁合金ZK60流变应力曲线的复杂性,通过加工图来分析热变形可加工性时,不能忽略应变的影响。
3 三维加工图及热变形行为分析
3.1 三维功率耗散图
从热模拟实验中采集合金在不同应变、应变速率和温度下的流变应力值,作出三维功率耗散图。图2所示为不同应变、不同温度和不同应变速率的三维功率耗散图,功率耗散图中具有不同灰度的网格点表示了各点的功率耗散值。

图2 不同应变、温度和应变速率的功率耗散图
Fig.2 3-D power dissipation maps at different strains, temperatures and strain rates: (a) At strain of 0.3 and 0.6; (b) At 240 and 300 ℃; (c) At strain rate of 0.03 and 0.3 /s
在功率耗散图中,随着应变的增加,在高温低应变速率下功率耗散值增加,在低温高应变速率下功率耗散值减少;随着变形温度的增加,功率耗散值增加;随着应变速率的增加,功率耗散值减少。镁合金ZK60的加工图呈现一个功率耗散的峰值区:温度300~360 ℃、应变速率为0.01~0.1 /s,耗散值平均为35%。由文献[11-12]可以发现,在此变形条件下镁合金发生了动态再结晶,当温度升高时,动态再结晶加快,此区域是最适合的热加工区。
3.2 三维失稳图及失稳判据分析
SEMIATIN和JONAS[13]指出流动软化与材料参数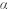 有关,
有关,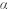 = -
= -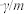 ,其中
,其中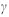 为流动软化速率
为流动软化速率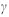 =
=  。流动局部化判据为
。流动局部化判据为
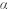 >5 (11)
>5 (11)
MURTHY[14]等根据J和η的定义:
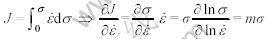
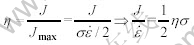
又根据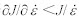 ,得到失稳判据为
,得到失稳判据为

GEGEL等[15-16]提出流变失稳与温度敏感度参数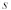 有关,
有关,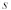 定义如下:
定义如下:
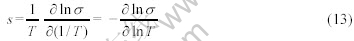
GEGEL等[15-16]考虑LYAPONOV函数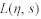 ,认为材料发生稳定流动,流变应力曲线是上凸的,流动应力随着温度的增加而降低,
,认为材料发生稳定流动,流变应力曲线是上凸的,流动应力随着温度的增加而降低,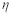 随
随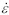 而降低,
而降低,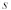 随
随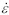 而降低。失稳判据为
而降低。失稳判据为
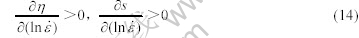
ALEXANDER[17]考虑了LYAPONOV函数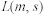 ,认为材料发生稳定流动,流变应力曲线是上凸的,流动应力随着温度的增加而降低,
,认为材料发生稳定流动,流变应力曲线是上凸的,流动应力随着温度的增加而降低,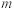 随
随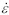 而降低,
而降低,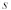 随
随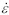 而降低。失稳判据为
而降低。失稳判据为
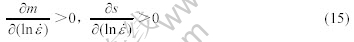
图3所示为依照不同失稳判据得到的流变失稳分布。在失稳图中,灰色区域为失稳区,在温度为200~360 ℃、应变速率为0.01~5 /s的变形条件下,随着应变的增加大部分区域都发生了失稳,加工的安全区是温度为300~360 ℃、应变速率为0.01~0.1 /s区域。由图3可以发现,依据的失稳判据不同得到的失稳区域不同。其中根据流动局部化判据得到的失稳区最小;根据MURTHY失稳判据和GEGEL失稳判据得到的失稳区很相似;根据ALEXANDER失稳判据,得出在温度300~350 ℃、应变速率为0.01~0.1 /s区域发生失稳,这与其它图都不相同。ZIEGLER失稳判据是根据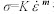 推导出来的,其成立的条件是流变应力满足本式的关系,不适合具有复杂应力应变曲线的金属如本研究的研究对象镁合金ZK60。流动局部化判据是经验公式,适用于平面压缩变形。MURTHY失稳判据基于大塑性变形连续理论,它不是经验公式,适用于任意类型的流变应力和应变速率曲线。GEGEL和Alexander的失稳判据都是依据LYAPONOV稳定性理论,但由于考虑的因素不同而显示不同的结果。总之,每一种判据都有其适用的范围,对于镁合金ZK60,MURTHY失稳判据和ALEXANDER失稳判据是适合的失稳判据,由于MURTHY失稳判据简单计算方便,适用于任意类型的流变应力曲线,具有较好的应用前景,本研究推荐使用这种失稳判据。
推导出来的,其成立的条件是流变应力满足本式的关系,不适合具有复杂应力应变曲线的金属如本研究的研究对象镁合金ZK60。流动局部化判据是经验公式,适用于平面压缩变形。MURTHY失稳判据基于大塑性变形连续理论,它不是经验公式,适用于任意类型的流变应力和应变速率曲线。GEGEL和Alexander的失稳判据都是依据LYAPONOV稳定性理论,但由于考虑的因素不同而显示不同的结果。总之,每一种判据都有其适用的范围,对于镁合金ZK60,MURTHY失稳判据和ALEXANDER失稳判据是适合的失稳判据,由于MURTHY失稳判据简单计算方便,适用于任意类型的流变应力曲线,具有较好的应用前景,本研究推荐使用这种失稳判据。

图3 基于不同失稳判据的三维失稳图
Fig.3 3-D flow instability maps through different instability criterions: (a) ZIEGLER’s instability criterion; (b) Flow localization criterion; (c) MURTHY’s instability criterion; (d) GEGEL’s instability criterion; (e) ALEXANDER’s instability criterion
4 三维加工图的绘制
4.1 实验数据的修正
在高应变速率加工时,产生的变形热来不及耗散会引起温度升高,而温升将导致流变应力下降,因此需对流变应力进行绝热修正。到目前为止,还没有正确的理论来指导流变应力的修正,PRASAD在论文中曾对应变速率为100 /s的流变应力增加5%来进行修正。通过对比原始流变应力数据(即修正后的数据减去自身的5%)绘制的加工图与修正的数据绘制的加工图,发现两者并没有明显的差别。但是当流变应力原始数据通过增加自身的10%进行修正时,未修正的失稳区比修正后的失稳区扩大了,尽管功率耗散图也有稍许变化,但其特征范围并没有改变。这说明在高应变速率条件下流变应力减小对加工图的失稳区有较大的影响,对功率耗散系数图影响不明显。对于材料加工来说,失稳变形必须避免,失稳区扩大有利于增加材料加工的安全性。由于镁合金的加工不能采用较快的加工速度,在本研究中,最大的应变速率为5.0 /s,所以用实测的流变应力来绘制加工图是可行的。
4.2 功率耗散系数和失稳参数的计算
加工图的计算过程如下:
1) 从实验中获得不同应变条件下恒定温度,恒定应变速率的流变应力值;
2) 根据实验数据,利用3次样条插值法计算出更小间隔的温度、应变速率所对应的流变应力值;
3) 固定每一温度对数据进行最小二乘三次多项式拟合,各变形温度下lg 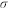 的大小可用lg
的大小可用lg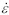 的多项式来表示:
的多项式来表示:
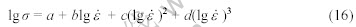
4) 计算不同应变条件下,应力应变速率敏感指数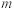 ,
,
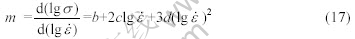
把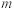 值代入公式(4),就得到不同变形温度和应变速率下,合金的能量耗散率。ZIEGLER失稳参数的计算式如下:
值代入公式(4),就得到不同变形温度和应变速率下,合金的能量耗散率。ZIEGLER失稳参数的计算式如下:

5) 同样固定每一温度对数据进行最小二乘三次多项式拟合,各变形温度下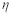 和
和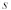 的大小可用lg
的大小可用lg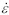 的多项式来表示,进而得到GEGEL判据。
的多项式来表示,进而得到GEGEL判据。
6) 以温度、应变速率和应变为坐标轴,采用三维色图绘制功率耗散图和失稳图;
4.3 功率耗散系数和失稳参数的修正
由镁合金ZK60的流变应力曲线可知,当温度较低时材料发生了断裂,取不同温度不同应变速率下材料发生断裂的极限应变,用3次样条插值法计算出更小间隔的温度、应变速率下的极限应变。在绘制功率耗散图时,认为当应变超过极限应变,功率耗散值为0;在绘制失稳图时,认为当应变超过极限应变时,材料发生失稳。
材料失稳通常认为是由于合金发生了绝热剪切带或局部流动。在小应变量下(达到峰值应力之前),由于加工硬化,随着应变的增加,流变应力和塑性功增加,材料不可能发生失稳。而根据失稳判据计算得到的结果显示,在低应变下,产生较大的失稳区。分析其原因为:失稳参数推导的基础是动态材料模型如公式(1)所示。经典理论认为在高温变形中,当材料发生动态再结晶时,在一定的温度下,流变应力是应变速率的函数,而在发生动态再结晶以前,材料以加工硬化和动态回复为主,在一定的温度和应变速率下,经典理论认为流变应力是应变的函数,如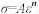 。因而当应变量较小时,需要对失稳参数进行修正,认为在应变到达峰值应变之前材料不发生流变失稳。
。因而当应变量较小时,需要对失稳参数进行修正,认为在应变到达峰值应变之前材料不发生流变失稳。
5 结论
1) 基于PRASAD所提出的二维加工图,建立了考虑应变的三维加工图,反映了在温度、应变速率和应变三维空间功率耗散系数和流变失稳区域的变化。
2) 针对ZK60流变应力曲线的复杂性,对根据流动局部化判据、MURTHY失稳判据、GEGEL失稳判据、ALEXANDER失稳判据得到的三维失稳图进行分析,得到了合适的失稳判据-MURHTY失稳判据。
3) 根据所绘制的三维加工图,确定了合适的加工区域温度为300~360 ℃、应变速率为0.01~0.1 /s。
REFERENCES
[1] FROST H J, ASHBY M F. Deformation mechanism maps[M]. Oxford, New York: Pergamon Press, 1982: 48-49.
[2] RAJ R. Development of a processing map for use in warm-forming and hot forming processes[J]. Metallurgy Transaction A, 1989, 12: 1089-1097.
[3] PRASAD Y V R K, SASIDHARA S. Hot working guide: A compendium of processing maps[M]. Metal Park, OH: ASM International, 1997: 1-24.
[4] PRASAD Y V R K, SESHACHARYULU T. Processing maps for hot working of titanium alloys[J]. Mater Sci Eng A, 1998, 243: 82-88.
[5] SIVAKESAVAM O, PRASAD Y V R K. Hot deformation behavior of as-cast Mg-2Zn-1Mn alloy in compression a study with processing map[J]. Mater Sci Eng A, 2003, 362: 118-124.
[6] PRASAD Y V R K. Processing maps: A status report[J]. Journal of Engineering and Performance, 2003, 12: 638-645.
[7] 汪凌云, 范永革, 黄光杰, 黄光胜. 镁合金AZ31B的高温 塑性变形及加工图[J]. 中国有色金属学报, 2004, 14(7): 1068-1072.
WANG Ling-yun, FAN Yong-ge, HUANG Guang-jie, HUANG Guang-sheng. Plastic deformation at elevated temperature and processing maps of magnesium alloy[J]. The Chinese Journal of Nonferrous Metals, 2004, 14 (7): 1068-1072.
[8] 鞠 泉, 李殿国, 刘国权. 15Cr-25Ni-Fe基合金高温塑性变形行为的加工图[J]. 金属学报, 2006, 42(2): 218-224.
JU Quan, LI Dian-guo, LIU Guo-quan. The processing map of hot plastic deformation of a 15Cr-25Ni-Fe based superalloy[J]. Acta Metallurgica Sinica, 2006, 42(2): 218-224.
[9] 鲍如强, 黄 旭, 曹春晓, 柯 俊. 加工图在钛合金的应用[J]. 材料导报报, 2004, 18(7): 26-29.
BAO Ru-qiang, HUANG Xu, CAO Chun-xiao, KE Jun. Application of processing maps in hot working of titanium alloy[J]. Materials Review, 2004, 18(7): 26-29.
[10] ZIEGLER H. An introduction to thermomechanics[M]. Amsterdam, New York, Oxford: North-holland Publishing Company, 1983.
[11] 张宪宏. 镁合金热变形过程试验研究和数值模拟[D]. 上海: 上海交通大学, 2004.
ZHANG Xian-hong. Experimental and numerical study of magnesium alloy during hot-working process[D]. Shanghai: Shanghai Jiao Tong University, 2004.
[12] GALIYEV A, KAIBYSHEV R, GOTTSTEIN G. Correlation of plastic deformation and dynamic recrystallization in magnesium alloy ZK60[J]. Acta Materrialia 1999, 47(14): 3753-3758.
[13] SEMIATIN S L, JONAS J J. Formability and workability of metals: Plastic instability and flow localization[M]. Metal Park, OH: ASM International, 1984: 51-78.
[14] NARAYANA MURTY S V S, NAGESWARRA RAO B, KASHYAP B P. Instability criteria for hot deformation of materials[J]. International Materials Reviews, 2000, 45(1): 15-26.
[15] GEGEL H L, MALAS J C, DORAIVELU S M, SHENDE V A. Modelling techniques used in forging process design in: Metals handbook, forming and forging[M]. (Vol.14). Metal Park, OH: ASM International, 1988: 417-438.
[16] GEGEL H L. Synthesis of atomistics and continuum modeling to describe microstructure: Computer simulation in material science[M]. Metal Park, OH: ASM International, 1987: 291-344.
[17] ALEXANDER J M. Mapping dynamic material behavior: Modelling hot deformation of steels[M]. Berlin: Springer-Verlag, 1989: 101-115.
收稿日期:2007-10-24;修订日期:2008-01-24
通讯作者:崔振山,教授,博士;电话:021-62827605;E-mail: cuizs@sjtu.edu.cn
(编辑 何学锋)