Kerosene-alumina nanofluid flow and heat transfer for cooling application
来源期刊:中南大学学报(英文版)2016年第4期
论文作者:M. Mahmoodi Sh. Kandelousi
文章页码:983 - 990
Key words:magnetic field; nanofluid; heat transfer; differential transformation method
Abstract: Kerosene-aluminananofluid flow and heat transfer in the presence of magnetic field are studied. The basic partial differential equations are reduced to ordinary differential equations which are solved semi analytically using differential transformation method. Velocity and temperature profiles as well as the skin friction coefficient and the Nusselt number are determined analytically. The influence of pertinent parameters such as magnetic parameter, nanofluid volume fraction, viscosity parameter and Eckert number on the flow and heat transfer characteristics is discussed. Results indicate that skin friction coefficient decreases with increase of magnetic parameter, nanofluid volume fraction and viscosity parameter. Nusselt number increases with increase of magnetic parameter and nanofluid volume fraction while it decreases with increase of Eckert number and viscosity parameter.
J. Cent. South Univ. (2016) 23: 983-990
DOI: 10.1007/s11771-016-3146-5

M. Mahmoodi1, Sh. Kandelousi2
1. Department of Aerospace Engineering, Malek-Ashtar University of Technology, Karaj, Tehran, Iran;
2. Department of Mechanical Engineering, Babol University of Technology, Babol, Iran
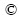 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: Kerosene-alumina nanofluid flow and heat transfer in the presence of magnetic field are studied. The basic partial differential equations are reduced to ordinary differential equations which are solved semi analytically using differential transformation method. Velocity and temperature profiles as well as the skin friction coefficient and the Nusselt number are determined analytically. The influence of pertinent parameters such as magnetic parameter, nanofluid volume fraction, viscosity parameter and Eckert number on the flow and heat transfer characteristics is discussed. Results indicate that skin friction coefficient decreases with increase of magnetic parameter, nanofluid volume fraction and viscosity parameter. Nusselt number increases with increase of magnetic parameter and nanofluid volume fraction while it decreases with increase of Eckert number and viscosity parameter.
Key words: magnetic field; nanofluid; heat transfer; differential transformation method
1 Introduction
Different types of cooling techniques are being used to protect the chamber and nozzle walls. In a typical cooling technique, like regenerative cooling, one of the propellants is passed through the coolant passage surrounding the wall of the nozzle. An innovative cooling system for semi-cryogenic engine needs to be explored by improving thermo-physical properties of kerosene, which can enhance the heat transfer capacity of kerosene. A recent way of improving the performance of these systems is to suspend metallic nanoparticles in the base fluid. SHEIKHOLESLAMI and ELLAHI [1] studied three dimensional mesoscopic simulation of magnetic field effect on natural convection of nanofluid. They found that thermal boundary layer thickness increases with increase of Lorentz forces. Force convective heat transfer of magnetic nanofluid in a lid driven semi annulus enclosure has been investigated by SHEIKHOLESLAMI et al [2]. Their results showed that Nusselt number has direct relationship with Reynolds number, nanoparticle volume fraction while it has reverse relationship with Hartmann number. Ferrofluid heat transfer treatment in the presence of variable magnetic field has been studied by SHEIKHOLESLAMI and RASHIDI [3]. They found that Nusselt number increases by considering magnetic field dependent viscosity. HATAMI et al [4] investigated the magnetohydrodynamic Jeffery-Hamel nanofluid flow in non-parallel walls. They found that skin friction coefficient is an increasing function of Reynolds number, opening angle and nanoparticle volume friction but decreasing function of Hartmann number. HATAMI et al [5] simulated the flow and heat transfer of nanofluid flow between two parallel plates. They showed that in order to reach the maximum Nusselt number, copper should be used as nanoparticle. Recently, several authors studied different passive methods to enhance the thermal performance [6-30].
Most phenomena in our world are essentially nonlinear and are described by nonlinear equations. Nonlinear differential equations usually arise from mathematical modeling of many physical systems. One of the semi-exact methods which doesn’t need small parameters is the differential transformation method. Therefore, same as the HAM and the HPM, the DTM can overcome the foregoing restrictions and limitations of perturbation methods. This method constructs an analytical solution in the form of a polynomial. It is different from the traditional higher-order Taylor series method. The Taylor series method is computationally expensive for large orders. The differential transform method is an alternative procedure for obtaining an analytic Taylor series solution of differential equations. The main advantage of this method is that it can be applied directly to nonlinear differential equations without requiring linearization, discretization and therefore, it is not affected by errors associated to discretization. The concept of DTM was first introduced by ZHOU [31], who solved linear and nonlinear problems in electrical circuits. HATAMI et al [32] used multi-step differential transformation method in order to investigate motion of a spherical particle in plane couette fluid flow. Semi analytical methods have been applied in various problems [33-44].
In this work, kerosene-alumina nanofluid flow and heat transfer in channel in the presence of magnetic field are investigated. DTM is applied to find the approximate solutions of nonlinear differential equations. The effects of the magnetic parameter, viscosity parameter, Eckert number and nanofluid volume fraction on flow and heat transfer characteristics are investigated.
2 Problem statement
Consider steady flow of nanofluid between two horizontal parallel plates (see Fig. 1). The origin is located at the lower plate, and the plates are located at y=0 and y=h. The lower plate is being stretched by two equal opposite forces so that the position of the point (0,0,0) remains unchanged. A uniform magnetic flux with density of B0 is acting along y-axis. Under these assumptions, the Navier–Stokes and energy equations are:
 (1)
(1)
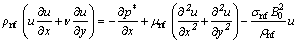 (2)
(2)
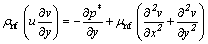 (3)
(3)
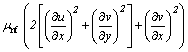 (4)
(4)
where u, v and w denote the fluid velocity components along the x, y and z directions, respectively; p* is the modified fluid pressure; T is temperature and the physical meanings of the other quantities are mentioned in the nomenclature. The corresponding boundary conditions of Eqs. (1)-(4) are:
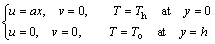 (5)
(5)
The effective density (ρnf), the effective dynamic viscosity (μnf), the effective heat capacity (ρCp)nf, the effective thermal conductivity (knf) and the electrical conductivity (snf) of the nanofluid are defined as
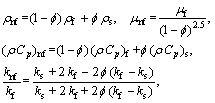
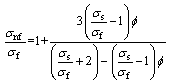 (6)
(6)
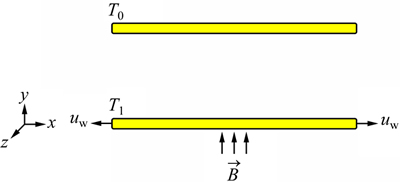
Fig. 1 Physical model along with coordinate system
The thermo-physical properties of the nanofluid are given in Table 1.
Table 1 Thermo-physical properties of water and nanoparticles

The following non-dimensional variables are introduced:
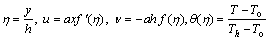 (7)
(7)
where the prime denotes differentiation with respect to η.
Therefore, the governing momentum and energy equations for this problem are given in dimensionless form by
 (8)
(8)
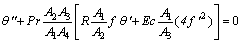 (9)
(9)
The dimensionless quantities in these equations are:
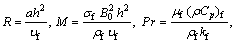
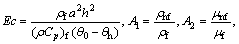
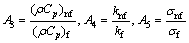 (10)
(10)
where R, M, Pr and Ec are viscosity parameter, magnetic parameter, Prandtl number and Eckert number, respectively.
The boundary conditions are:
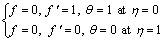 (11)
(11)
The physical quantity of interest in this problem is the skin friction coefficient Cf along the stretching wall, which is defined as
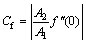 (12)
(12)
The Nusselt number at the lower plate is defined as
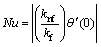 (13)
(13)
3 Differential transform method (DTM)
3.1 Basic of DTM
Basic definitions and operations of differential transformation are introduced as follows. Differential transformation of the function f(η) is defined as
 (14)
(14)
In Eq. (14), f(η) is the original function and F(k) is the transformed function which is called the T-function (it is also called the spectrum of the f(η) at η-η0, in the k domain). The differential inverse transformation of F(k) is defined as
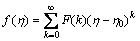 (15)
(15)
by combining Eqs. (14) and (15), f(η) can be obtained as
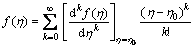 (16)
(16)
Equation (16) implies that the concept of the differential transformation is derived from Taylor’s series expansion, but the method does not evaluate the derivatives symbolically. However, relative derivatives are calculated by an iterative procedure that is described by the transformed equations of the original functions. From the definitions of Eqs. (14) and (15), it is easily proven that the transformed functions comply with the basic mathematical operations shown in below. In real applications, the function f(η) in Eq. (16) is expressed by a finite series and can be written as
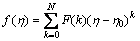 (17)
(17)
Equation (16) implies that 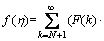
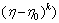 is negligibly small, where N is series size.
is negligibly small, where N is series size.
Theorems to be used in the transformation procedure, which can be evaluated from Eqs. (14) and (15), are given in Table 2.
3.2 Solution with differential transformation method
Now, differential transformation method has been applied into governing equations (Eqs. (8) and (9)). Taking the differential transforms of equations (8) and (9) with respect to χ and considering H=1 gives:
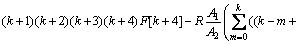
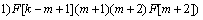
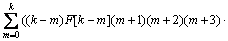
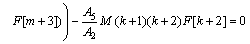 (18)
(18)
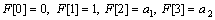 (19)
(19)
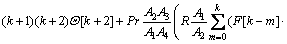
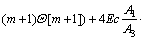
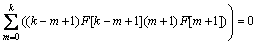 (20)
(20)
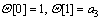 (21)
(21)
where F[k] and Θ[k] are the differential transforms of f(η), θ(η), respectively; and a1, a2, a3 are constants which can be obtained through boundary condition. This problem can be solved as follows:
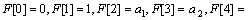
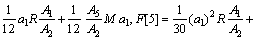
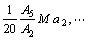 (22)
(22)

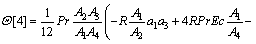
 (23)
(23)
The above process is continuous. By substituting eqs. (22) and (23) into the main equation Eq. (17) based on DTM, it can be obtained that the closed form of the solutions is:

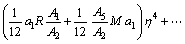 (24)
(24)
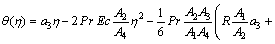
 (25)
(25)
by substituting the boundary condition from Eq. (11) into eqs. (24) and (25) at point η=1, it can be obtained the values of a1, a2, a3. By substituting obtained a1, a2, a3 into eqs. (24) and (25), it can be obtained the expression of F(η) and Θ(η).
Table 2 Some of basic operations of differential transformation method

4 Results and discussion
In this work, kerosene-alumina nanofluid flow and heat transfer in presence of magnetic field are investigated. The basic partial differential equations are reduced toordinary differential equations. Differential transformation method is used to solve the governing equations. Effects of magnetic parameter, alumina volume fraction, viscosity parameter and Eckert number on flow and heat transfer are investigated. In order to verify the accuracy of the present results, we have compared the results for the temperature profiles with those reported by SHEIKHOLESLAMI and GANJI [45] when f=0 (regular or Newtonian fluid). This comparison shows an excellent agreement (Fig. 2).
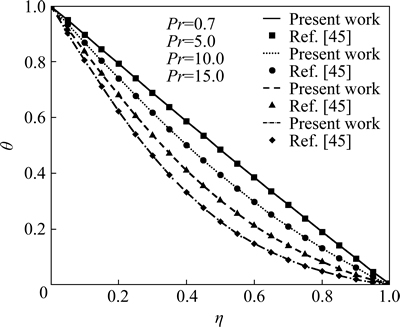
Fig. 2 Comparison of temperature profiles between present work and Ref. [45] when λ=0. 5, M=1, R=0.5 and Kr=0.5
Effects of magnetic number and viscosity parameter on velocity profiles and skin friction coefficient are shown in Figs. 3 and 4. As magnetic parameter increases, Lorentz forces increases. So, flow suppressed and in turn skin friction coefficient decreases with increase of magnetic field. Velocity boundary layer thickness near the lower plate increases with increase of viscosity parameter and in turn skin friction coefficient decreases with increase of this parameter. Also, it can be found that skin friction coefficient decreases with increase of nanofluid volume fraction.
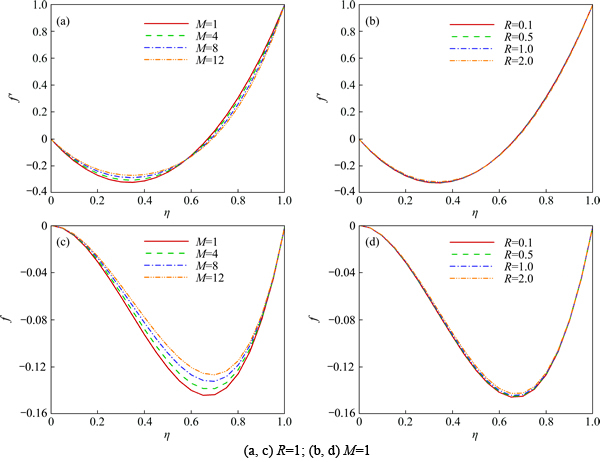
Fig. 3 Effects of magnetic parameter and viscosity parameter on velocity profiles when f=0.04:
Effects of magnetic number, nanofluid volume fraction, viscosity parameter and Eckert number on temperature profile and Nusselt number are shown in Figs. 5 and 6, respectively. Effects of magnetic number and nanofluid volume fraction on temperature profile are similar together. It means that thermal boundary layer thickness near the hot wall decreases with increase of these parameters. So, Nusselt number increases with rise of magnetic number and nanofluid volume fraction. As viscosity parameter increases, temperature increases and in turn rate of heat transfer decreases with augment of viscosity parameter. Temperature increases with increase of vicious dissipation. So, Nusselt number decreases with increase of Eckert number.
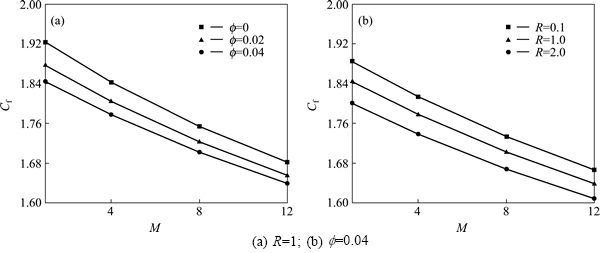
Fig. 4 Effects of magnetic parameter, nanofluid volume fraction, and viscosity parameter on skin friction coefficient:

Fig. 5 Effects of magnetic parameter, nanofluid volume fraction, viscosity parameter and Eckert number on temperature profiles when Pr=21.976:
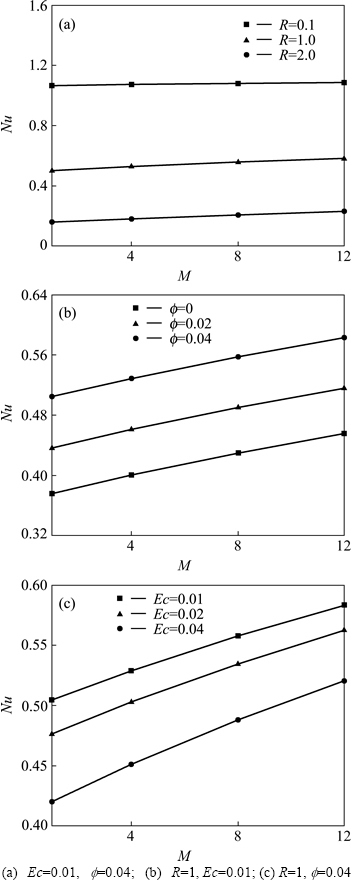
Fig. 6 Effects of magnetic parameter, nanofluid volume fraction, viscosity parameter and Eckert number on Nusselt number when Pr=21.976:
5 Conclusions
kerosene-alumina nanofluid flow and heat transfer in a channel in the presence of magnetic field are investigated. Differential transformation method is used to solve the governing equations. The effect of the magnetic parameter, nanofluid volume fraction, viscosity parameter and Eckert number on heat and fluid flow are investigated. The following results have been obtained. Differential transformation method has good agreement. Using kerosene-alumina nanofluid as fuel of liquid rocket engine can improve the cooling process of chamber and nozzle walls. Nusselt number increases with increase of alumina volume fraction in kerosene but opposite trend is observed for skin friction coefficient. Nusselt number increases with increase of magnetic parameter while it decreases with increase of Eckert number.
Nomenclature
A1, A2, A3, A4, A5
dimensionless constants
Cf
skin friction coefficients
Cp
specific heat capacity at constant pressure
Ec
Eckert number
f(η)
similarity function
h
distance between plates
K
thermal conductivity
M
Magnetic parameter
Nu
Nusselt number
p
modified fluid pressure
Pr
Prandtl number
R
Viscosity parameter
u,n
velocity components along x, y, respectively
Greek symbols
α
thermal diffusivity
f
nanoparticle volume fraction
η
Dimensionless variable
μ
dynamic viscosity
υ
kinematic viscosity
θ
dimensionless temperature
s
Electrical conductivity
ρ
fluid density
τw
skin friction or shear stress along stretching surface
Subscripts
nf
nanofluid
f
base fluid
s
nano-solid-particles
References
[1] SHEIKHOLESLAMI M, ELLAHI R. Three dimensional mesoscopic simulation of magnetic field effect on natural convection of nanofluid [J]. International Journal of Heat and Mass Transfer, 2015, 89: 799-808.
[2] SHEIKHOLESLAMI M, RASHIDI M M, GANJI D D. Effect of non-uniform magnetic field on forced convection heat transfer of Fe3O4- water nanofluid [J]. Comput Methods Appl Mech Engrg, 2015, 294: 299-312.
[3] SHEIKHOLESLAMI M, RASHIDI M M. Ferrofluid heat transfer treatment in the presence of variable magnetic field [J]. Eur Phys J Plus, 2015: 130-115.
[4] HATAMI M, SHEIKHOLESLAMI M, HOSSEINI M, GANJI C C. Analytical investigation of MHD nanofluid flow in non-parallel walls [J]. Journal of Molecular Liquids, 2014, 194: 251-259.
[5] HATAMI M, SHEIKHOLESLAMI M, GANJI D D. Nanofluid flow and heat transfer in an asymmetric porous channel with expanding or contracting wall [J]. Journal of Molecular Liquids, 2014, 195: 230-239.
[6] HATAMI M, GANJI D D. Heat transfer and flow analysis for SA-TiO2 non-Newtonian nanofluid passing through the porous media between two coaxial cylinders [J]. Journal of Molecular Liquids, 2013, 188: 155-161.
[7] HATAMI M, GANJI D D. Natural convection of sodium alginate (SA) non-Newtonian nanofluid flow between two vertical flat plates by analytical and numerical methods [J]. Case Studies in Thermal Engineering, 2014, 2: 14-22.
[8] SHEIKHOLESLAMI M, GANJI D D. Entropy generation of nanofluid in presence of magnetic field using Lattice Boltzmann Method [J]. Physica A, 2015, 417: 273-286.
[9] SHEIKHOLESLAMI M, GORJI-BANDPY M, VAJRAVELU K. Lattice Boltzmann simulation of magnetohydrodynamic natural convection heat transfer of Al2O3-water nanofluid in a horizontal cylindrical enclosure with an inner triangular cylinder [J]. International Journal of Heat and Mass Transfer, 2015, 80: 16-25.
[10] SHEIKHOLESLAMI M, GANJI D D, YOUNUS JAVED M, ELLAHI R. Effect of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer by means of two phase model [J]. Journal of Magnetism and Magnetic Materials, 2015, 374: 36-43.
[11] SHEIKHOLESLAMI M, ABELMAN S, GANJI D D. Numerical simulation of MHD nanofluid flow and heat transfer considering viscous dissipation [J]. International Journal of Heat and Mass Transfer, 2014, 79: 212-222.
[12] ZHANG Chao-li, ZHENG Lian-cun, ZHANG Xin-xin, CHEN Gong. MHD flow and radiation heat transfer of nanofluids in porous media with variable surface heat flux and chemical reaction [J]. Applied Mathematical Modelling, 2015, 39: 165-181.
[13] HUSSAIN T, SHEHZAD S A, ALSAEDI A, HAYAT T, RAMZAN M. Flow of Casson nanofluid with viscous dissipation and convective conditions: A mathematical model [J]. Journal of Central South University, 2015, 22: 1132-114.
[14] SHEIKHOLESLAMI M, GANJI D D. Ferrohydrodynamic and magnetohydrodynamic effects on ferrofluid flow and convective heat transfer [J]. Energy, 2014, 75: 400-410.
[15] SHEIKHOLESLAMI M, GORJI-BANDPY M, GANJI D D. Review of heat transfer enhancement methods: Focus on passive methods using swirl flow devices [J]. Renewable and Sustainable Energy Reviews, 2015, 49: 444-469.
[16] SHEIKHOLESLAMI M, RASHIDI M M. Effect of space dependent magnetic field on free convection of Fe3O4-water nanofluid [J]. Journal of the Taiwan Institute of Chemical Engineers, 2015, DOI: 10.1016/j.jtice.2015.03.035.
[17] SHEIKHOLESLAMI M, GORJI BANDPY M, ASHORYNEJAD H R. Lattice Boltzmann method for simulation of magnetic field effect on hydrothermal behavior of nanofluid in a cubic cavity [J]. Physica A: Statistical Mechanics and its Applications, 2015, 432: 58-70.
[18] SHEIKHOLESLAMI M, ELLAHI R. Simulation of ferrofluid flow for magnetic drug targeting using Lattice Boltzmann method [J]. Journal of Zeitschrift Fur Naturforschung A, 2015, 70(2): 115-124.
[19] ASHORYNEJAD H R, MOHAMAD A A, SHEIKHOLESLAMI M. Magnetic field effects on natural convection flow of a nanofluid in a horizontal cylindrical annulus using Lattice Boltzmann method [J]. International Journal of Thermal Sciences, 2013, 64: 240-250.
[20] SHEIKHOLESLAMI M, GORJI-BANDPAY M, GANJI D D. Magnetic field effects on natural convection around a horizontal circular cylinder inside a square enclosure filled with nanofluid [J]. International Communications in Heat and Mass Transfer, 2012, 39: 978-986.
[21] SHEIKHOLESLAMI M, HATAMI M, JAFARYAR M, FARKHADNIA F, GANJI D D, GORJI-BANDPY M. Thermal management of double-pipe air to water heat exchanger [J]. Energy and Buildings, 2015, 88: 361-366.
[22] SHEIKHOLESLAMI KANDELOUSI M. Effect of spatially variable magnetic field on ferrofluid flow and heat transfer considering constant heat flux boundary condition [J]. The European Physical Journal Plus, 2014, 18: 129-248.
[23] SHEIKHOLESLAMI M, GORJI-BANDPY M, GANJI D D. Lattice Boltzmann method for MHD natural convection heat transfer using nanofluid [J]. Powder Technology, 2014, 254: 82-93.
[24] RAHMAN M M,  ZTOP H F, STEELE M, NAIM A G, AL-SALEM K H, IBRAHIM T A. Unsteady natural convection and statistical analysis in a CNT–water filled cavity with non-isothermal heating [J]. International Communications in Heat and Mass Transfer, 2015, 64: 50-60.
ZTOP H F, STEELE M, NAIM A G, AL-SALEM K H, IBRAHIM T A. Unsteady natural convection and statistical analysis in a CNT–water filled cavity with non-isothermal heating [J]. International Communications in Heat and Mass Transfer, 2015, 64: 50-60.
[25] SHEHZAD S A, HUSSAIN T, HAYAT T, RAMZAN M, ALSAEDI M. Boundary layer flow of third grade nanofluid with Newtonian heating and viscous dissipation [J]. Journal of Central South University, 2015, 22: 360-367.
[26] SHEIKHOLESLAMI M, HATAMI M, GANJI D D. Nanofluid flow and heat transfer in a rotating system in the presence of a magnetic field [J]. Journal of Molecular Liquids, 2014, 190: 112-120.
[27] SHEIKHOLESLAMI M, GORJI-BANDPY M, GANJI D D. Numerical investigation of MHD effects on Al2O3-water nanofluid flow and heat transfer in a semi-annulus enclosure using LBM [J]. Energy, 2013, 60: 501-510.
[28] HATAMI M, GANJI D D. Motion of a spherical particle on a rotating parabola using Lagrangian and high accuracy multi-step differential transformation method [J]. Powder Technology, 2014, 258: 94-98.
[29] HAYAT T, NAZ R, ASGHAR S, MESLOU S. Soret–Dufour effects on three-dimensional flow of third grade fluid [J]. Nuclear Engineering and Design, 2012, 243: 1-14.
[30] SHEIKHOLESLAMI M, ABELMAN S. Two phase simulation of nanofluid flow and heat transfer in an annulus in the presence of an axial magnetic field [J]. IEEE Transactions on Nanotechnology, 2015, 14(3): 561-569.
[31] ZHOU K. Differential transformation and its applications for electrical circuits [M]. Wuhan: Huazhong Univ Press, 1986.
[32] HATAMI M, SHEIKHOLESLAMI M, DOMAIRRY G. High accuracy analysis for motion of a spherical particle in plane couette fluid flow by multi-step differential transformation method [J]. Powder Technology, 2014, 260: 59-67.
[33] HATAMI M, GANJI D D. Thermal behavior of longitudinal convective-radiative porous fins with different section shapes and ceramic materials (SiC and Si3N4) [J]. Ceramics International, 2014, 40: 6765-6775.
[34] SHEIKHOLESLAMI M, GANJI D D, ASHORYNEJAD H R. Investigation of squeezing unsteady nanofluid flow using ADM [J]. Powder Technology, 2013, 239: 259-265.
[35] HATAMI M, GANJI D D. Investigation of refrigeration efficiency for fully wet circular porous fins with variable sections by combined heat and mass transfer analysis [J]. International Journal of Refrigeration, 2014, 40: 140-151.
[36] SHEIKHOLESLAMI M, GANJI D D. Heat transfer of Cu-water nanofluid flow between parallel plates [J]. Powder Technology, 2013, 235: 873-879.
[37] MAKINDE OD, OSALUSI E. MHD steady flow with slip in a channel with permeable boundaries [J]. Romanian Journal of Physics, 2006, 51(3/4): 293-302.
[38] NIU J, ZHENG L, YANG Y, SHU C H. Chebyshev spectral method for unsteady axisymmetric mixed convection heat transfer of power law fluid over a cylinder with variable transport properties [J]. Int J Numer Anal Model, 2014, 11: 525-540.
[39] SHEIKHOLESLAMI M, RASHIDI M M, AL SAAD D M, FIROUZI F, ROKNI H B, DOMAIRRY G. Steady nanofluid flow between parallel plates considering thermophoresis and Brownian effects [J]. Journal of King Saud University-Science, 2015, doi:10.1016/j.jksus.2015.06.003.
[40] SHEIKHOLESLAMI M, GANJI D D. Nanofluid flow and heat transfer between parallel plates considering Brownian motion using DTM [J]. Comput Methods Appl Mech Engrg, 2015, 283: 651-663.
[41] SHEIKHOLESLAMI M, GANJI D D, RASHIDI M M. Ferrofluid flow and heat transfer in a semi annulus enclosure in the presence of magnetic source considering thermal radiation [J]. Journal of the Taiwan Institute of Chemical Engineers, 2015, 47: 6-17.
[42] SHEIKHOLESLAMI M, KANDELOUSI M. KKL correlation for simulation of nanofluid flow and heat transfer in a permeable channel [J]. Physics Letters A, 2014, 378(45): 3331-3339.
[43] ELLAHI R, MUBASHIR BHATTI M, RIAZ A, SHEIKHOLESLAMI M. Effects of magnetohydrodynamics on peristaltic flow of jeffrey fluid in a rectangular duct through a porous medium [J]. Journal of Porous Media, 2014, 17(2): 143-157.
[44] HATAMI M, GANJI D D. Motion of a spherical particle in a fluid forced vortex by DQM and DTM [J]. Particuology, 2014, 16: 206-212.
[45] SHEIKHOLESLAMI M, GANJI D D. Three dimensional heat and mass transfer in a rotating system using nanofluid [J]. Powder Technology, 2014, 253: 789-796.
(Edited by YANG Hua)
Received date: 2015-03-25; Accepted date: 2015-07-31
Corresponding author: Sh. Kandelousi, Lecture; M. Mahmoodi, Assistant Professor; Tel: +98-2636102789; E-mail: mostafamahmoodi@mut.ac.ir (M. Mahmoodi), m.Kandelousi.sh@gmail.com (Sh. Kandelousi)

