J. Cent. South Univ. (2017) 24: 625-636

DOI: 10.1007/s11771-017-3463-3

Natural frequencies analysis of a composite beam consisting of Euler-Bernoulli and Timoshenko beam segments alternately

PENG Li-ping(彭利平)^{1, 2}, JI Ai-min(纪爱敏)¹, ZHAO Yue-min(赵跃民)², LIU Chu-sheng(刘初升)³

1. College of Mechanical and Electrical Engineering, Hohai University, Changzhou 213022, China;

2. School of Chemical Engineering and Technology, China University of Mining and Technology,

Xuzhou 221116, China;

3. School of Mechatronic Engineering, China University of Mining and Technology, Xuzhou 221116, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2017

Abstract: Present investigation is concerned with the free vibration property of a beam with periodically variable cross-sections. For the special geometry characteristic, the beam was modelled as the combination of long equal-length uniform Euler-Bernoulli beam segments and short equal-length uniform Timoshenko beam segments alternately. By using continuity conditions, the hybrid beam unit (ETE-B) consisting of Euler-Bernoulli beam, Timoshenko beam and Euler-Bernoulli beam in sequence was developed. Classical boundary conditions of pinned-pinned, clamped-clamped and clamped-free were considered to obtain the natural frequencies. Numerical examples of the equal-length composite beam with 1, 2 and 3 ETE-B units were presented and compared with the equal-length and equal-cross-section Euler-Bernoulli beam, respectively. The work demonstrates that natural frequencies of the composite beam are larger than those of the Euler-Bernoulli beam, which in practice, is the interpretation that the inner-welded plate can strengthen a hollow beam. In this work, comparisons with the finite element calculation were presented to validate the ETE-B model.

Key words: natural frequency; Euler-bernoulli beam; Timoshenko beam; hybrid beam unit; composite beam

1 Introduction

Beam structures are widely-used structural components in mechanical, civil and aerospace engineering [1-3]. Most transverse vibration analysis of beam has been conducted on the basis of the classical Euler-Bernoulli beam theory. However, if the cross-sectional dimensions are not small to the length of the beam, the effects of rotary inertia and shear deformation should be taken into account, as the Timoshenko beam theory describes [4]. The Timoshenko model is a major improvement for non-slender or short beams [5, 6]. When a hollow beam is fabricated with an inner-welded plate, it can be treated as a kind of composite beam.

Vibration of a composite beam with varying cross- section has received enough scientific attention. The Adomian decomposition method (ADM) is employed by MAO et al [7, 8] to investigate the free vibrations of a stepped Euler-Bernoulli beam with two uniform sections and further to study multiple-stepped beams with arbitrary boundary conditions. JAWORSKI et al [9] presented the flexural-free vibration of a cantilevered beam with multiple cross-section steps theoretically and experimentally, in which the Rayleigh-Ritz method and component modal analysis were adopted. KWON et al [10] focused on the dynamic characteristics of the frame consisting of two stepped beams and a rigid body connecting each beam tip. NAGULESWARAN [11] proposed an analytical method to calculate the frequencies of beams with up to three step changes in cross-section and later presented the vibration of beams with up to three-step changes in cross-section and in which the axial force in each portion is constant but different [12]. DUAN et al [13] developed a modified discrete singular convolution to analyze the free vibration of beams with multiple step changes successfully. Among the above publications, only transverse vibration of Euler-Bernoulli beam is discussed, and these beams are all solid ones and effects of rotary inertia and shear deformation are negligible.

Figure 1(a) depicts a hollow uniform beam with a rectangular cross-section and length L. On the condition that the whole length is constant, the beam in Fig. 1(a) can be replaced by the composite beam welded by two equal-length long hollow uniform beams with length l_E1 and a short solid uniform beam with length l_T1 (Fig. 1(b)), or by (n+1) equal-length long hollow uniform beam with length l_En and n short solid uniform beams with length l_Tn (Fig. 1(e)), where n is number of the short solid uniform beams and n is set to be 2 and 3 in Figs. 1(c) and (d) for example, respectively. Figure 1(f) depicts construction of the composite beam studied in this work in detail. Long hollow Euler-Bernoulli beam (EB) segments and short solid Timoshenko beam (TB) segments are arranged in turn and in sequence and then connected by weld at peripheries of the contact areas F₁, F₂, …, F_2j-1, F_2j, …, F_2n-1, F_2n. To simplify the description, these beam segments are named as EB-1, TB-2, EB-3, …, EB-2j-1, TB-2j, EB-2j+1, …, EB-2n-1, TB-2n, EB-2n+1 according to the geometry characteristic and order the beam segment. All EB segments are equal-length and all TB segments are equal-length, namely, l₁=l₃=…=l_2j-1= l_2j+1=…=l_2n-1=l_2n+1, and l₂=l₄=…=l_2j=…=l_2n-2=l_2n. Considering the special geometric construction, the hybrid beam unit consisting of Euler-Bernoulli beam, Timoshenko beam and Euler-Bernoulli beam (ETE-B) is extracted and then the whole composite beam can be divided into ETE-B-1, ETE-B-2, ···, ETE-B-j, ···, ETE-B-n. , where the serial number j is half that of the corresponding TB-2j. Now take the ETE-B-j for example,cross-section dimensions of the EB-2j-1, TB-2j, EB-2j+1 in ETE-B-j are all b (width)×h (height) and the thickness of all hollow EB segments is h₀.

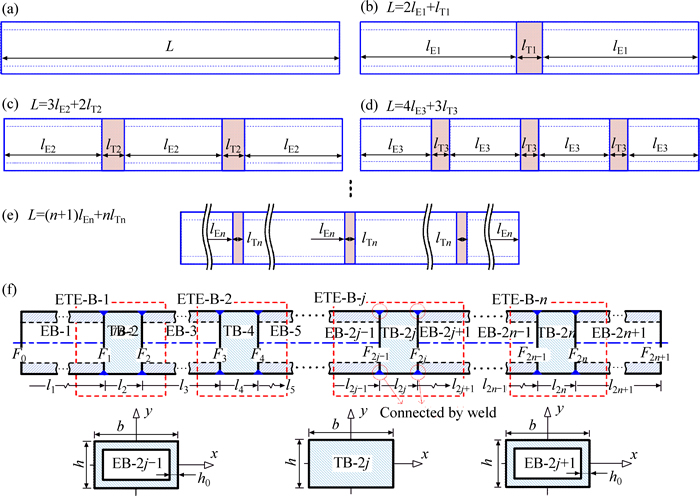
Fig. 1 Composite beam consisting of long hollow EB segments and short solid TB segments (not drawn to scale)

In this work, we consider eigenvalue problem of a composite beam consisting of long equal-length EB segments and short equal-length TB segments alternately. A special hybrid beam unit ETE-B is developed. The analysis is based on the classical Euler-Bernoulli beam theory and Timoshenko beam theory.

2 Dynamics equation for ETE-B model

Without loss of generality, consider the free vibration of a hybrid beam unit (ETE-B-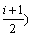 including EB-i, TB-i+1 and EB-i+2, as shown in Fig. 2. To write the equations of transverse vibrations of the hybrid beam unit, three coordinate systems are established with origin at left end of each beam segment. Thus transverse vibrations of EB-i, TB-i+1 and EB-i+2 at time t are y_i(x, t) at axial coordinate x (0i), y_i+1(x, t) at axial coordinate x (0i₊₁) and y_i+2(x, t) at axial coordinate x (0i₊₂). l_i, l_i+1 and l_i+2 are the length of EB-i, TB-i+1 and EB-i+2, respectively, and l_i=l_i+2. As shown, ρ is the density of the beam material; E and G are the elastic modulus and the shear modulus of the beam material, respectively; κ is the shear correction factor of TB-i+1 and κ=10(v+1)/ (11v+12) for a rectangular cross-section, where v is the Poisson ratio; I_i, I₊₁ and I_i+2 are the cross-sectional moment of inertia of EB-i, TB-i+1 and EB-i+2, respectively, and I_i+1=bh³/12, I_i=I_i+2=bh³/12-(b-2h₀)·(h-2h₀)³/12, where h₀ is the thickness of EB segments. A_i, A_i+1 and A_i+2 are the cross-sectional area of EB-i, TB-i+1 and EB-i+2, respectively, and A_i+1=bh, A_i=A_i+2=bh-(b- 2h₀)(h-2h₀).

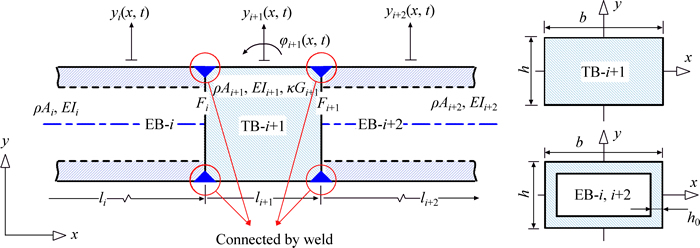
Fig. 2 A hybrid beam unit ETE-B- and corresponding cross-section (not drawn to scale)

2.1 Euler-Bernoulli beam segment (EB-i)

The equation for the free transverse vibration y_i(x, t) of the EB-i segment is given in the following form [4]:

with    (1)

Usually y_i(x, t) has sinusoidal form and can be treated as product of a modal function Y_i(x, t) and a sine function sin(ωt) with angular frequency ω. By introducing the frequency variable λ and the following expression:

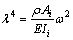                                (2)

the problem under consideration is governed by the following differential equation:

                          (3)

where primes denote differentiation with respect to x.

The solution of Eq. (3) has both sinusoidal and hyperbolic terms:

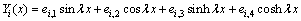 (4)

where e_i,1, e_i,2, e_i,3 and e_i,4 are modal coefficients determined by boundaries for EB-i.

With the serial number i varying, the analysis for EB-i above can be extended to the other EB segments in the whole composite beam.

2.2 Timoshenko beam segment (TB-i+1)

Consider the free transverse vibration of the TB-i+1 segment in ETE-B- The two coupled equations describing the transverse vibration of the beam y_i+1(x, t) and the angle of rotation of the cross-section φ_i+1(x, t) due to bending of the beam at position x and time t are given by

,

                             (5)

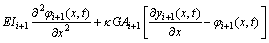
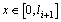,             (6)

Similarly, with the sinusoidal motion with an angular frequency ω assumed for TB-i+1 and the modal transverse vibration function Y_i+1(x) and modal rotation function f_i+1(x) used, Eqs. (5) and (6) are derived as

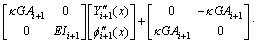
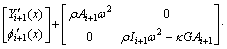
                         (7)

Introducing the following expressions:

,

,

,

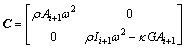
and substituting them into Eq. (7), then we have:

                          (8)

                         (9)

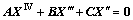                      (10)

Equations (8)-(10) result in the two uncoupled equations describing the free motion of TB-i+1 in matrix form, i.e.

                        (11)

where

             (12)

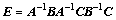                         (13)

Expanding Eq. (11) and we have

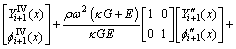
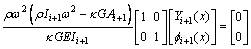  (14)

which clearly demonstrates that the differential equations for Y_i+1(x) and f_i+1(x) have the same form. Thus we can assume the solutions of Eq. (11) to be

                         (15)

where U and r are the eigenvectors and eigenvalues, respectively. Substituting Eq. (15) into Eq. (11) yields

       (16)

In order to have a non-trivial solution, the determinant of the above matrix has to be zero, that is,

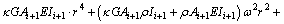
            (17)

whose number of roots is four.

With a given material and geometry of the beam, we may have [15]:

                        (18)

then the first two imaginary solutions of Eq. (17) are computed by

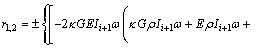
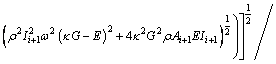
                         (19-1)

and rewritten to be

                               (19-2)

where

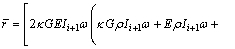
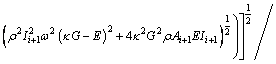
                          (19-3)

and i is imaginary unit given as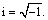

Next, the remaining two real solutions of Eq. (17) are computed by

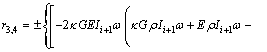
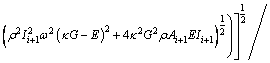
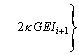                         (20-1)

and rewritten as

                                 (20-2)

where

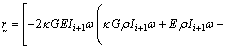
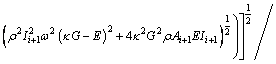
                           (20-3)

The solution of Eq. (11) also has both sinusoidal and hyperbolic terms, and can be expressed as

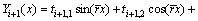
           (21)

Using Eq. (21) and Eq. (7) yields the expression for modal rotation function, that is

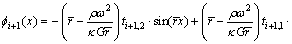
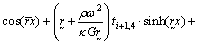
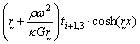             (22)

where t_i+1,1, t_i+1,2, t_i+1,3 and t_i+1,4 are modal coefficient determined by boundaries for TB-i+1.

With the serial number i varying, the analysis for TB-i+1 above can be extended to the other TB segments in the whole composite beam.

3 Continuity conditions and classical boundary conditions

3.1 Continuity conditions

For the hybrid beam unit ETE-B- shown in Fig. 2, continuity of displacement and continuity of slope at cross-section Fi (Fi=(EB-i) ∩ (TB-i+1) and “∩” reprents the interconnection) together with compatibility of shearing forces and bending moments for the two adjacent beam segments (EB-i and TB-i+1) results in

           (23-1)

         (23-2)

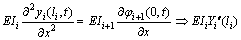
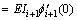       (23-3)

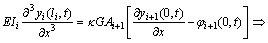
      (23-4)

The continuity conditions at position x=l_i+1 of TB-i+1 and position x=0 of EB-i+2 can be obtained in a similar way, i.e.

     (24-1)

    (24-2)

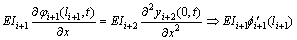
                       (24-3)

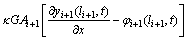
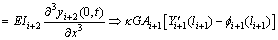
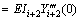                       (24-4)

Substituting Eq. (4) for EB-i, Eqs. (21), (22) for TB-i+1 and the transformational Eq.(4) for EB-i+2 into Eqs. (23.1)-(24.4), and introducing the vectors 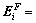and 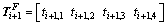, the continuity conditions can be written in a matrix form. First we obtain the following modal coefficient continuity vector for cross-section Fi=(EB-i) ∩ (TB-i+1),

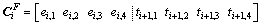
                         (25-1)

 (25-2)

and the corresponding modal shape continuity matrix Similarly, with the serial number i varying, the modal coefficient continuity vector and the corresponding modal shape continuity matrix for cross-section Fi₊₁=(TB-i+1) ∩ (EB-i+2) can be written according to Eq. (25-1) and given by

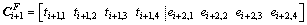
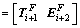       (26-1)

and

 (26-2)

respectively.

Therefore, the continuity conditions for the hybrid beam unit ETE-B-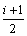 are written in a matrix form, namely,

                            (27-1)

where

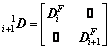                       (27-2)

is the modal continuity characteristic matrix of ETE-B-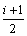 and

          (27-3)

is the modal coefficient continuity vector of ETE-B- Notice that the left subscript “i+1” is same as the series number of the first TB segment in composite beam and the left superscript “1” is the number of the ETE-B unit. The following relationship between and exists:

                            (27-4)

Here we give another example to demonstrate the application of ETE-B units. A composite beam with twohybrid beam units (ETE-B- ETE-B-is shown in Fig. 3. ETE-B-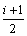 consists of EB-i, TB-i+1 and EB-i+2. ETE-B- 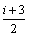consists of EB-i+2, TB-i+3 and EB-i+4. The modal continuity characteristic matrix and the corresponding modal coefficient continuity vector of the composite beam in Fig. 3 are, respectively:

 (28-1)

and

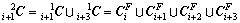
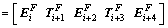           (28-2)

which satisfy the following relationship:

                            (28-3)

The same procedure may be followed to express the mode shape of the composite beam in Fig. 1(f), which consists of n ETE-B units and each unit has the same type and the same number of components. The modal continuity characteristic matrix and the corresponding modal coefficient continuity vector are, respectively:

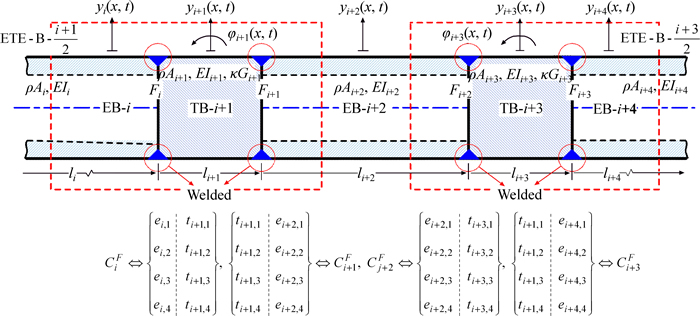
Fig. 3 A composite beam with two hybrid beam units (ETE-B-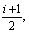 ETE-B- 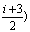and corresponding modal continuity coefficient vector (not drawn to scale)

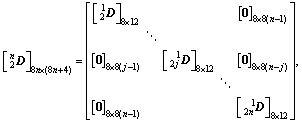
                     (29-1)

and

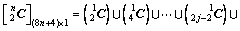
   (29-2)

And the two matrices are related by

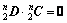                              (29-3)

3.2 Classical boundary conditions

The boundary conditions at left end of the whole composite beam shown in Fig. 1(f) are assumed to be clamped (CL) and pinned (PL) while those at the right end are clamped (CR), pined (PR) and free (FR). Transverse vibration for EB-1 at x=0 are both zero. The slope and the bending moment at left end is zero for clamped case and pined case, respectively. Hence, we have

CL:  (30-1)

PL:  (30-2)

The right coordinate of the right end is x=l_2n+1 for EB-2n+1. Similarly, transverse vibration of CR and PR are both zero. The slope and the bending moments are zero for CR and PR, respectively. The shearing force and bending moment for FR are both zero. We further obtain

CR: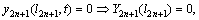

     (31-1)

PR: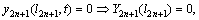

    (31-2)

FR: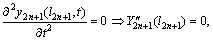

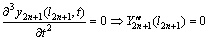    (31-3)

By introducing the transformational terms of Eq. (4) for EB-1 and EB-2n+1 into Eqs. (30)-(31) and extracting the trigonometric functions of the variant λ, we have

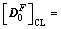
 (32-1)

for CL,

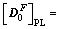
 (32-2)

for PL,

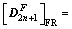
 (33-1)

for FR,

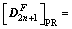
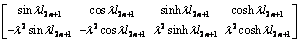 (33-2)

for PR, and

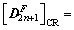
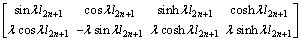 (33-3)

for CR.

Aiming at the composite beam with n ETE-B units and the boundary conditions above, the characteristic matrix can be obtained by adding the matrices (32-1)- 33-3) into the modal continuity characteristic matrix of Eq. (29-1), i.e.

 (34)

and the characteristic coefficient vector is the same as the modal coefficient continuity vector of Eq. (29-2), namely:

                     (35)

The following relationship for the characteristic matrix and the characteristic coefficient vector holds:

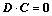                                  (36)

Finally for different boundary condition cases, one can obtain the angular frequency ω of the composite beam in Fig. 1(f) by numerically solving the following frequency equation:

                              (37)

where ω can be used to calculate the natural frequency f_n by f_n=2π/ω.

Since D in Eq. (36) is singular at each angular frequency ω, Eq. (37) is an indeterminate equation and the unknown parameters in C cannot be directly determined. However, one may choose one quantity of any element in C as the arbitrary nonzero constant, then the other elements can be solved from Eq. (36). In this work, the first element in C is set to be 1 for the other elements solved. After that, substituting the elements in C into the corresponding modal function of each beam segment yields the modal shape of the whole composite beam.

4 Numerical examples

The natural frequencies are important since a structure may resonate catastrophically under dynamic loads. Numerical experiments based on the theoretical ETE-B model and the commercial finite element software ANSYS/Workbench are conducted to illustrate the feasibility and accuracy of the analysis in the sections above. Using the expressions of the developed ETE-B model, a MATLAB code has been developed to obtain the natural frequencies. Here, the solution flow chart for the frequency variable λ is demonstrated in Fig. 4. It should be mentioned that the reason to choose λ as an iteration variable instead of the angular frequency ω is to simplify the calculation. The number of ETE-B units (denoted by n) used for constructing the composite beam to be studied should be first determined, which leads to establishing the and in Eq. (29-3). Then with the classical boundary conditions determined, the corresponding boundary condition matrices among Eqs. (32-1)-(33-3) will be added into to obtain D in Eq. (34), whose size is (8n+4)×(8n+4). As the frequency equation is a complicated indeterminate one, λ is set to vary from 0 to a threshold value λ_t with an interval △λ. When λ=λ₀, and if f (λ₀)×f (λ₀+△λ)<0, then we may conclude that a feasible solution for Eq. (37) lies in the range [λ₀, λ₀+△λ]. Such procedure will be repeated to have all the appropriate solution ranges found with λ varying from 0 to λ_t, and further the Bisection method [16] and Eq. (2) are introduced to obtain all the roots, namely, f_n in each solution range. Notice that the threshold value λ_t is just determined by trial computations.

In the rest part, numerical examples of three composite beams together with an equal-length and equal-cross-section hollow Euler-Bernoulli beam (short for E) are given. The three composite beams consist of 1 ETE-B unit (short for ETE-1), 2 ETE-B units (short for ETE-2) and 3 ETE-B units (short for ETE-3), respectively. The beam material is stainless steel with ρ=7750 kg/m³ and E=193 GPa. Table 1 summarizes the geometric parameters for each beam. In the numerical examples, natural frequencies of these beams would be presented by the finite element method and the theoretical ETE-B model.

The results of the finite element calculations were performed by ANSYS/Workbench to validate the analytic one. The three composite beams were developed by three-dimensional modeling directly. To simulate the practical welting processing during the composite beam manufacturing, the EB segments and the TB segment were connected by “spot welt” command in the software, as Fig. 5 shows.

Fig. 4 Solution flow chart for natural frequency calculation (E_ps is threshold error, which is set to be 0.0001 in this work)

Table 1 Geometric parameters of ETE-1, ETE-2, ETE-3 and E

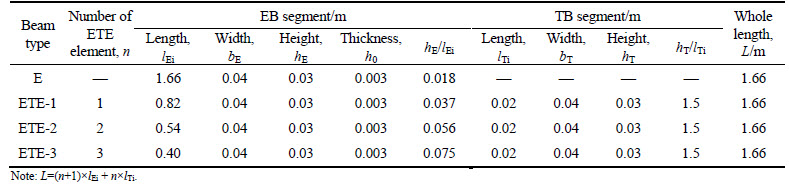
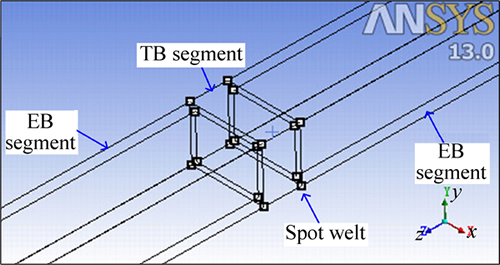
Fig. 5 ETE beam model in finite element software

In particular, with TB segments not introduced, the composite beam can be modelled as a totally equal-length Euler-Bernoulli beam. Natural frequencies of such beams with different classical boundary conditions would be obtained by the traditionally Euler-Bernoulli beam theory [4], as Table 2 shows. The values of λ_iL at any mode number i is substitute into the natural frequency formula to yield the corresponding natural frequency.

Tables 3-5 reveal the first four natural frequencies for the composite beams (ETE-1, ETE-2 and ETE-3) and the equal-length hollow Euler-Bernoulli beam (E) with different classical boundary conditions (CL-FR, PL-PR and CL-CR). The relative increasements of natural frequencies of ETE-1, ETE-2 and ETE-3 to those of E are shown in Fig. 6. In these numerical examples, the frequency interval △λ and the threshold value λ_t are set to be 20, respectively.

The results of E in Tables 3-5 are exactly the same for the classical Euler-Bernoulli theory and the ETE-B model, respectively. It confirms the derivation accuracy of the ETE-B model. Together with Fig. 6, we can conclude that the natural frequency differences between the ETE-B model and the ANSYS are general small for CL-FR and PL-PR cases, while the maximum difference can be up to 14% in a CL-CR ETE-3. In fact, in this numerical example, with three Timoshenko beam segments introduced into ETE-3, the whole slender beam is bearing a significant concentrated mass simultaneously, which is considered in the ETE-B model. Thus, the model is more effective in a composite beam with one or two Timoshenko beam segments.

Table 2 Values of λ_iL in general computation formula for natural frequencies of a beam with classic boundary conditions

Table 3 First four natural frequencies of ETE-1, ETE-2, ETE-3 and E under CL-FR

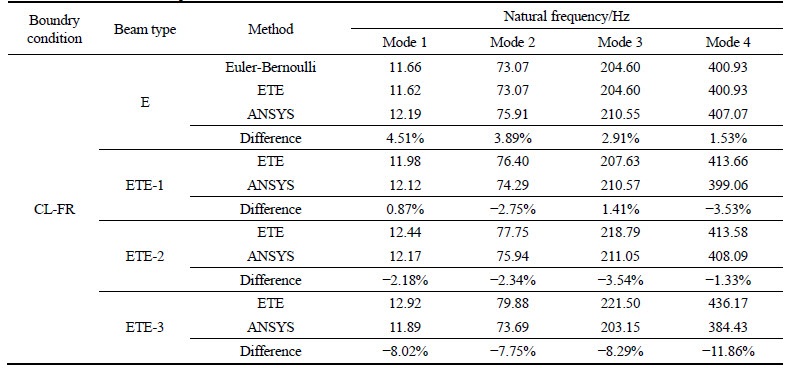
Table 4 First four natural frequencies of ETE-1, ETE-2, ETE-3 and E under CL-FR

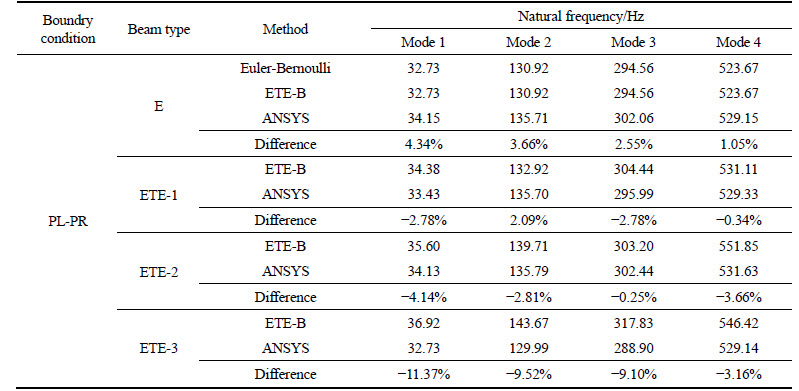
Figure 7 plots the increasement of the first four ETE-B model-based natural frequencies of ETE-1,ETE-2 and ETE-3 to those of E. It is noted that natural frequencies of ETE-1, ETE-2 and ETE-3 are all larger than those of E and the larger the number of ETE-B units is, the larger the natural frequencies are. This is attributed to the TB segments increase the rigidity of the whole hollow Euler-Bernoulli beam. The notable exceptions are the 3rd natural frequency of PL-PR ETE-1, the 4th natural frequency of PL-PR ETE-2, the 4th natural frequency of CL-FR ETE-1, which are larger than the corresponding natural frequencies of the composite beam with one more ETE-B unit.

Table 5 First four natural frequencies of ETE-1, ETE-2, ETE-3 and E under CL-FR

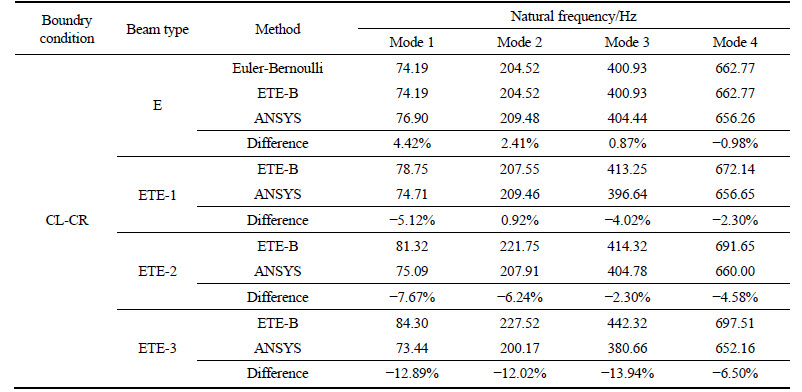
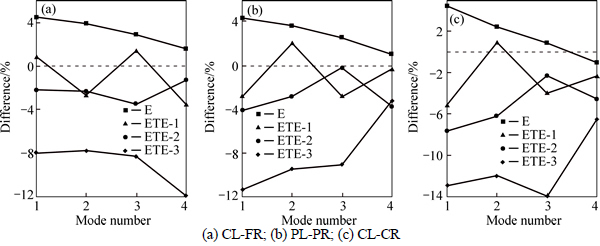
Fig. 6 Relativity error of natural frequencies of ETE-1, ETE-2, ETE-3 and E obtained by theoretical ETE-B to those by ANSYS:

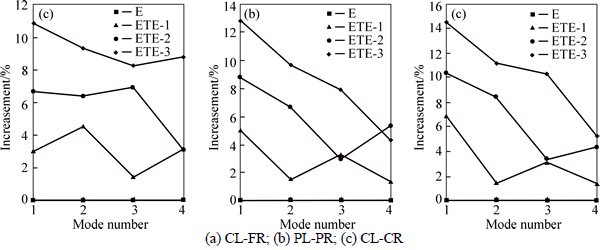
Fig. 7 Increasement of first four model-based natural frequencies of ETE-1, ETE-2 and ETE-3 to those of E:

5 Conclusions

1) A hybrid beam unit consisting of Euler-Bernoulli beam, Timoshenko beam and Euler-Bernoulli beam (ETE) in sequence are developed.

2) The frequency equations of a composite beam modelled as the combination of long equal-length Euler- Bernoulli beam segments and short equal-length Timoshenko beam segments alternately are derived and solved by numerical methods.

3) TB segments has the characteristics of strengthening the beam. Natural frequencies of the composite beam are larger than those of the equal-length and equal-cross-section Euler-Bernoulli beam and the larger the number of ETE units is, the larger these natural frequencies are. The theoretical derivation and conclusions may be used in engineering application.

References

[1] HSU J C, LAI H Y, CHEN C K. An innovative eigenvalue problem solver for free vibration of uniform Timoshenko beams by using the Adomian modified decomposition method [J]. Journal of Sound and Vibration, 2009, 325(1): 451-470.

[2] LU Z R, HUANG M, LIU J K, CHEN W H, LIAO W Y. Vibration analysis of multiple-stepped beams with the composite element model [J]. Journal of Sound and Vibration, 2009, 322(4): 1070-1080.

[3] ANDERSON C S, SEMERCIGIL S E, TURAN F. Vibration suppression of stepped beams: New designs for hot-wire probes [J]. Journal of Sound and Vibration, 2005, 282(1): 197-214.

[4] GINSBERG J H. Mechanical and structural vibrations: Theory and applications [M]. John Wiley & Sons Incorporated, 2001.

[5] HAN M S, BENAROYA H, WEI T. Dynamics of transversely vibrating beams using four engineering theories [J]. New York: Journal of Sound and Vibration, 1999, 225(5): 935-988.

[6] THALAPIL J, MAITI S K. Detection of longitudinal cracks in long and short beams using changes in natural frequencies [J]. International Journal of Mechanical Sciences, 2014, 83: 38-47.

[7] MAO Q, PIETRZKO S. Free vibration analysis of stepped beams by using Adomian decomposition method [J]. Applied Mathematics and Computation, 2010, 217(7): 3429-3441.

[8] MAO Q. Free vibration analysis of multiple-stepped beams by using Adomian decomposition method [J]. Mathematical and Computer Modelling, 2011, 54(1): 756-764.

[9] JAWORSKI J W, DOWELL E H. Free vibration of a cantilevered beam with multiple steps: Comparison of several theoretical methods with experiment [J]. Journal of Sound and Vibration, 2008, 312(4): 713-725.

[10] KWON H D, PARK Y P. Dynamic characteristics of stepped cantilever beams connected with a rigid body [J]. Journal of Sound and Vibration, 2002, 255(4): 701-717.

[11] NAGULESWARAN S. Vibration and stability of an Euler-Bernoulli beam with up to three-step changes in cross-section and in axial force [J]. International Journal of Mechanical Sciences, 2003, 45(9): 1563-1579.

[12] NAGULESWARAN S. Vibration of an Euler-Bernoulli beam on elastic end supports and with up to three step changes in cross- section [J]. International Journal of Mechanical Sciences, 2002, 44(12): 2541-2555.

[13] DUAN G, WANG X. Free vibration analysis of multiple-stepped beams by the discrete singular convolution [J]. Applied Mathematics and Computation, 2013, 219(24): 11096-11109.

[14] XU S, WANG X. Free vibration analyses of Timoshenko beams with free edges by using the discrete singular convolution [J]. Advances in Engineering Software, 2011, 42(10): 797-806.

[15] RENSBURG V, MERWE D. Natural frequencies and modes of a Timoshenko beam [J]. Wave Motion, 2006, 44(1): 58-69.

[16] HAHN B, VALENTINE D. Essential MATLAB for Engineers and Scientists [M]. Salt Lake: Academic Press, 2013.

(Edited by FANG Jing-hua)

Cite this article as: PENG Li-ping, JI Ai-min, ZHAO Yue-min, LIU Chu-sheng. Natural frequencies analysis of a composite beam consisting of Euler-Bernoulli and Timoshenko beam segments alternately [J]. Journal of Central South University, 2017, 24(3): 625-636. DOI: 10.1007/s11771-017-3463-3.

Foundation item: Projects(51605138, U1508210) supported by the National Natural Science Foundation of China; Project(BK20160286) supported by the Natural Science Foundation of Jiangsu Province, China; Project(2015B30214) supported by the Fundamental Research Funds for the Central Universities, China

Received date: 2015-09-24; Accepted date: 2016-03-22

Corresponding author: ZHAO Yue-min, Professor, PhD; Tel: +86-516-83590092; E-mail: ymzhao_paper@126.com