弹性支承块式轨道在高速列车作用下的动力响应分析

赫丹^{1, 2}，向俊¹，曾庆元¹

 (1. 中南大学 土木建筑学院，湖南 长沙，410075；

2. 中国中铁二院工程集团有限责任公司 重庆设计研究院，重庆 410015)

摘  要：为研究高速列车-弹性支承块式无碴轨道系统的动力学性能，提出一种竖向振动分析方法。其原理是：将高速列车的动车和拖车模拟为具有二系悬挂的多刚体系统；将弹性支承块式无碴轨道模拟为具有24个自由度的轨段单元的集合；基于弹性系统动力学总势能不变值原理及形成系统矩阵的“对号入座”法则，建立此系统竖向振动矩阵方程，并采用Wilson-θ数值积分法求解，计算速度为200 km/h时此系统竖向动力响应，研究轨道刚度对此系统竖向振动响应的影响规律。研究结果表明：钢轨竖向位移最大为1.125 mm，支承块竖向位移最大值为0.522 mm，并且计算波形图可以反映列车编组；钢轨扣件竖向刚度的合理取值范围为60~80 kN/mm，块下垫层的竖向刚度宜大于80 kN/mm。

关键词：无碴轨道；轨段单元；竖向振动；轨道刚度

中图分类号：U213.2          文献标志码：A         文章编号：1672-7207(2010)02-0770-05

Dynamic response analysis of low vibration track subjected to
 high-speed train

HE Dan^{1, 2}, XIANG Jun¹, ZENG Qing-yuan¹

(1. School of Civil and Architectural Engineering, Central South University, Changsha 410075, China;

2. Chongqing Design and Research Institute, China Railway Eryuan Engineering Group Co.Ltd.,
 Chongqing 410015, China )

Abstract: An analysis method for vertical vibration of high-speed train (HST) and low vibration track (LVT) system was proposed to study the dynamic performance of the system. Both motor car and each trailer of HST were modeled as a multi-rigid-body system with two suspensions, and LVT was modeled as an assembly of track segment elements with 24 degrees of freedom. The vertical vibration matrix equation of the system was established on the basis of the principle of  the total potential energy with stationary value in elastic system dynamics and the rule of “set-in-right-position” for formulating system matrixes, and then Wilson-θ numerical integration method was used to solve the problem. The dynamic responses of the system were calculated when the train runs at the speed of 200 km/h. And the effects of vertical stiffness of rail fastener and block pad on vertical vibration responses of the system were investigated. The results show that the maximum vertical displacements of rail and block are 1.125 mm and 0.522 mm, respectively, and the calculated waveforms can reflect train formation. The reasonable range of vertical stiffness of rail fastener is 60-80 kN/mm, and that of block pad should be bigger than 80 kN/mm.

Key words: ballastless track; track segment element; vertical vibration; track stiffness

我国客运专线轨道结构以区段铺设无碴轨道为 主^[1]，因此，高速列车与无碴轨道动力相互作用问题得到高度重视^[2]。为了解无碴轨道动力特性必需对高速列车-无碴轨道系统振动进行分析。弹性支承块式无碴轨道作为一种新型无碴轨道结构，具有减小养护维修工作量、提高轨道结构弹性和减振降噪等优   点，在铁路隧道和城市轨道交通建设中得到了广泛应用。众多学者针对此种轨道结构进行了大量研究，如：王继军^[3]进行了静、动力理论计算和试验验证；王祥秋等^[4]利用有限元法分析了其动力响应特征；谷爱军等^[5]建立了其竖向振动分析模型；朱剑月等^[6]利用落轴冲击从理论上分析了其动力性能；江成等^[7]通过实尺模型室内试验对其整体性能进行了研究。但上述工作并未将高速列车与无碴轨道视为一个整体运动系统加以研究，从而未能全面评价列车-轨道系统的动力学性能。为了研究高速列车-弹性支承块式无碴轨道系统的动力学性能，本文作者将列车与轨道视为一个整体系统，提出高速列车-弹性支承块式无碴轨道系统竖向振动分析方法，计算此系统竖向振动响应，同时，还对轨道刚度对此系统竖向振动响应的影响规律进行分析。

1  分析方法

1.1  高速列车竖向振动分析模型

本文以“中华之星”高速列车(编组为1动+4拖)为例，将其动车及拖车均离散为具有二系悬挂的多刚体系统。其中，车体及转向架均考虑浮沉和点头这2个自由度，每个轮对仅考虑浮沉这1个自由度。这样，每辆车共有10个自由度。有了此位移模式，就可以推导出第j辆车的竖向振动总势能П_Vj，具体推导过程见文献[8-9]。

1.2  弹性支承块式轨道竖向振动分析模型

1.2.1  轨段单元模型

针对弹性支承块式无碴轨道的结构特点，提出具有24个自由度的弹性支承块式轨道竖向振动轨段单元模型，如图1所示。

沿轨道纵向，取相邻2个扣件间的轨道为1个轨段单元(实际上是一小段轨道)。在每个单元中，钢轨视为弹性点支承Euler梁，通过扣件与轨下支承块连接；轨下支承块视为刚体质量块，通过垫层与道床板连接；将扣件和垫层均模拟为线性弹簧和黏滞阻尼器，将道床板与混凝土基座视为一个整体，置于弹性路基(视为线性均布面弹簧和黏滞阻尼器)上，并采用横向有限条与板段单元法^[10-13]对道床板进行竖向位移插值。取下列变位参数描述轨段单元的节点位移：

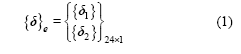
其中：

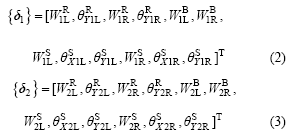
式中：上标R，B和S分别表示钢轨、支承块和道床板；下标1和2分别表示X轴方向上轨段单元的左端节点和右端节点；下标L和R分别表示Y轴方向上轨段单元的左边和右边；W表示沿Z轴方向的线位移；θ表示转角。

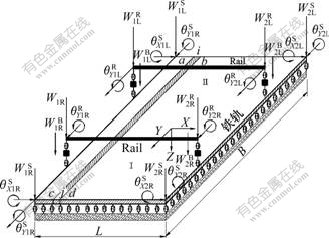
图1  弹性支承块式轨道竖向振动轨段单元模型

Fig.1  Model of track segment element for
vertical vibration of LVT

1.2.2  位移模式

钢轨上任一点处的竖向位移通过Hermite 3次方插值函数插值得到；支承块具有独立的竖向位移自由度；道床板的竖向位移通过如下方法得到。

如图1所示，在道床板中沿Y轴方向任取一横向有限条abcd，当其宽度较小时可视为梁段ij，则其上任一点的竖向位移可用其两端点i和j的变位参数并采用Hermite 3次方插值函数插值得到，而i和j的变位参数又可用单元节点变位参数经插值得到，其中，线位移采用Hermite 3次方插值函数插值得到，转角采用线性插值得到。最后，可得用轨段单元节点位移表示的道床板竖向位移的表达式。这种道床板竖向位移插值方法称为横向有限条与板段单元法，与一般的板单元的插值方法相比，具有简单、实用的特点。

1.2.3  竖向振动总势能

在确定轨段单元中每一部件的位移模式后，就可以推导出其中的钢轨及道床板的竖向弹性变形能及惯性力势能、支承块的竖向惯性力势能、钢轨扣件及块下垫层和路基表层的竖向弹性变形能及阻尼力势能。将上述单元中各部件的势能相加，即可得到第i个轨段单元的竖向振动总势能П_Ti。设弹性支承块式无碴轨道计算范围内共有N_Z个轨段单元，则整个轨道竖向振动总势能为：

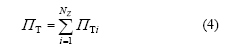
1.3  系统竖向振动方程的建立及求解

设在t时刻轨道计算长度范围内有M辆车，则此时轨道上列车的竖向振动总势能为：

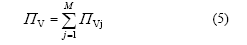
系统在t时刻的竖向振动总势能为：

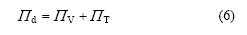
根据弹性系统动力学总势能不变值原理^[14]及形成系统矩阵的“对号入座”法则^[15]，即可得出系统在t时刻的竖向振动矩阵方程：

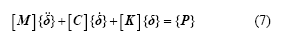
式中：[M]，[C]和[K]分别为系统竖向振动的质量、阻尼及刚度矩阵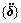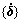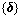；，，和{P}分别为系统竖向振动的加速度、速度、位移及荷载列阵。采用Wilson-θ数值积分法求解方程(7)。

2  分析实例

本文计算了“中华之星”高速列车(编组为1动+4拖)以200 km/h速度在弹性支承块式无碴轨道上运行时的系统竖向振动响应具有代表性的计算波形，如图2和图3所示。从图2和图3可以看出：位移计算结

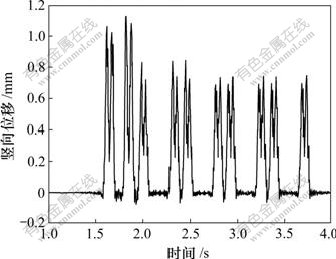
图2  钢轨竖向位移波形

Fig.2  Wave of vertical displacement of rail

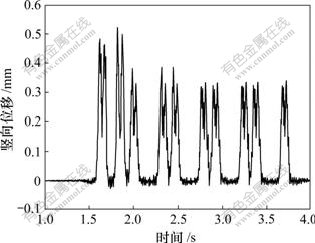
图3  支承块竖向位移波形

Fig. 3  Wave of vertical displacement of block

果在通常范围内，各响应波形符合客观实际结果；钢轨和支承块竖向位移最大值分别为1.125 mm和0.522 mm。例如，对于钢轨某一处来说，当列车车轮经过该处时，钢轨竖向位移均较大；当车轮在该处之前及之后时，钢轨竖向位移均很小，甚至为0；另外，从图2和图3中还可数出列车车辆的数目以及列车何时通过钢轨观察点。以上结果表明本文方法正确、可靠。

3  轨道刚度对系统振动响应的影响

3.1  钢轨扣件竖向刚度的影响

固定其他计算参数，只变化钢轨扣件竖向刚度K_u，则钢轨竖向位移、支承块竖向位移、动车轮轨竖向力和轮重减载率最大值与K_u的关系分别如图4~7所示。由图4~7可见：钢轨竖向位移、动车轮轨竖向力及轮重减载率最大值均随K_u的增大而减小，其中，位移最大可减小56%，减载率可减小38%，变化明显。只有支承块竖向位移随K_u的增大而增大，这说明K_u不宜过大，否则会增大支承块的竖向位移，在不利情况下会导致支承块破坏，故K_u应有合理取值范围。

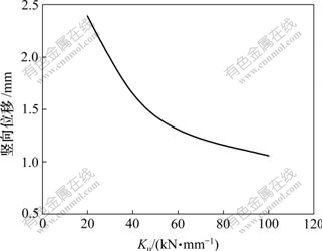
图4  钢轨竖向位移与扣件竖向刚度K_u的关系曲线

Fig.4  Relationship between vertical displacement of
rail and K_u

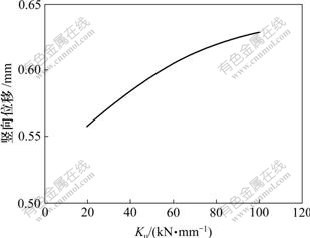
图5  支承块竖向位移与刚件竖向刚度K_u的关系曲线

Fig.5  Relationship between vertical displacement of
 block and K_u

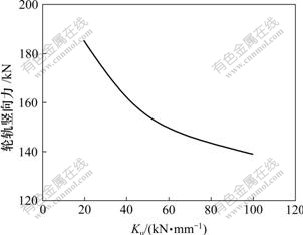
图6  动车轮轨竖向力与刚件竖向刚度K_u的关系曲线

Fig.6  Relationship between vertical wheel-rail force of
motor car and K_u

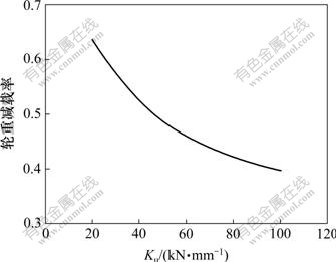
图7  动车轮重减载率与K_u的关系曲线

Fig.7  Relationship between wheel load reduction rate of motor car and K_u

3.2  块下垫层竖向刚度的影响

固定其他计算参数，只变化块下垫层竖向刚度K_m，则钢轨竖向位移、支承块竖向位移、动车轮轨竖向力与K_m的关系分别如图8~10所示。由图8~10可见：钢轨及支承块竖向位移、动车轮轨竖向力均随K_m的增大而减小，且K_m对前两者影响较大，钢轨及支承块竖向位移最多可分别减小33%和57%。因此，块下垫层竖向刚度应较大为宜。

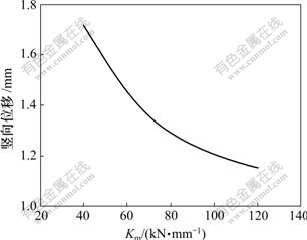
图8  钢轨竖向位移与垫层竖向刚度K_m的关系曲线

Fig.8  Relationship between vertical displacement of
 rail and K_m

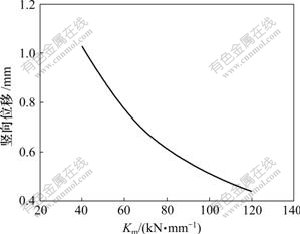
图9  支承块竖向位移与垫层竖向刚度K_m的关系曲线

Fig.9  Relationship between vertical displacement of
block and K_m

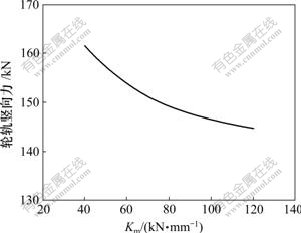
图10  动车轮轨竖向力与垫层竖向刚度K_m的关系曲线

Fig.10  Relationship between vertical wheel-rail force of motor car and K_m。

4  结论

 (1) 提出了高速列车-弹性支承块式无碴轨道系统竖向振动分析方法，计算了“中华之星”高速列车以200 km/h通过弹性支承块式无碴轨道时的系统竖向振动响应，钢轨和支承块竖向位移最大值分别为1.125 mm和0.522 mm。计算结果表明：本方法正确、可行，能够较好地反映轨道的动力特性。

(2) 得出钢轨扣件竖向刚度的合理取值范围为60~80 kN/mm，块下垫层的竖向刚度宜大于80 kN/mm，这样有利于减小轨道振动，延长其使用寿命。

参考文献：

[1] 何华武. 我国客运专线应大力发展无碴轨道[J]. 中国铁路, 2005, 44(1): 11-15.
HE Hua-wu. Ballastless track shall be developed in great efforts on Chinese passenger dedicated lines[J]. Chinese Railways, 2005, 44(1): 11-15.

[2] 赵国堂. 高速铁路无碴轨道结构[M]. 北京: 中国铁道出版社, 2006: 95-104.
ZHAO Guo-tang. Ballastless track structure of high-speed railway[M]. Beijing: China Railway Press, 2006: 95-104.

[3] 王继军. 弹性支承块式无碴轨道结构及其动力性能的研究[D]. 北京: 铁道科学研究院, 1999: 22-54.
WANG Ji-jun. Research on dynamic performances of LVT structure[D]. Beijing: China Academy of Railway Sciences, 1999: 22-54.

[4] 王祥秋, 杨林德, 高文华. 基于变分原理的整体道床结构动力有限元分析[J]. 振动与冲击, 2005, 24(4): 99-102.
WANG Xiang-qiu, YANG Lin-de, GAO Wen-hua. Dynamic FEM analysis for the integration ballast structure based on vibration principle[J]. Journal of Vibration and Shock, 2005, 24(4): 99-102.

[5] 谷爱军, 范俊杰. 随机荷载作用下地铁隧道内弹性支承块式轨道的竖向振动传力分析[C]//2005全国博士生学术论坛(交通运输工程学科)论文集. 北京: 中国铁道出版社, 2006: 1311-1314.
GU Ai-jun, FAN Jun-jie. Analysis of the vertical vibration transmission force of LVT track in tunnel under the random load[C]//Proceedings of 2005 Doctoral Forum of China. Beijing: China Railway Press, 2006: 1311-1314.

[6] 朱剑月, 练松良. 弹性支承块轨道结构落轴冲击动力性能分析[J]. 中国铁道科学, 2006, 27(3): 22-26.
ZHU Jian-yue, LIAN Song-liang. Analysis on the dynamic characteristics of low vibration track by use of wheel load drop[J]. China Railway Science, 2006, 27(3): 22-26.

[7] 江成, 林之珉. 高速铁路无碴轨道结构的试验研究[J]. 中国铁路, 2000, 39(7): 22-24.
JIANG Cheng, LIN Zhi-min. Test and research on the ballastless track structure for high-speed railway[J]. Chinese Railways, 2000, 39(7): 22-24.

[8] 李德建. 列车-轨道时变系统空间振动分析[D]. 长沙: 长沙铁道学院土木建筑学院, 1996: 60-80.
LI De-jian. Dynamic analysis of train-track space-coupling time-varying system[D]. Changsha: School of Civil and Architectural Engineering, Changsha Railway University, 1996: 60-80.

[9] 曾庆元, 向俊, 周智辉, 等. 列车脱轨分析理论与应用[M]. 长沙: 中南大学出版社, 2006: 204-207.
ZENG Qing-yuan, XIANG Jun, ZHOU Zhi-hui, et al. Analysis theory and application of train derailment[M]. Changsha: Central South University Press, 2006: 204-207.

[10] XIANG Jun, HE Dan, ZENG Qing-yuan. Analysis theory of spatial vibration of high-speed and slab track system[J]. Journal of Central South University of Technology, 2008, 15(1): 121-126.

[11] 向俊, 赫丹, 曾庆元. 横向有限条与无砟轨道板段单元的车轨系统竖向振动分析法[J]. 铁道学报, 2007, 29(4): 64-69.
XIANG Jun, HE Dan, ZENG Qing-yuan. Analysis method of vertical vibration of train and ballastless track system with the lateral finite strip and slab segment element[J]. Journal of the China Railway Society, 2007, 29(4): 64-69.

[12] 向俊, 赫丹. 高速列车与博格板式轨道系统竖向振动分析模型[J]. 交通运输工程学报, 2007, 7(3): 1-5.
XIANG Jun, HE Dan. Analysis model of vertical vibration of high-speed train and B?gl slab track system[J]. Journal of Traffic and Transportation Engineering, 2007, 7(3): 1-5.

[13] 赫丹, 向俊, 曾庆元. 一种无碴轨道动力学建模的新方法[J]. 中南大学学报: 自然科学版, 2007, 38(6): 1206-1211.
HE Dan, XIANG Jun, ZENG Qing-yuan. A new method for dynamics modeling of ballastless track[J]. Journal of Central South University: Science and Technology, 2007, 38(6): 1206-1211.

[14] ZENG Qing-yuan, LOU Ping, XIANG Jun. The principle of total potential energy with stationary value in elastic system dynamics and its application to the analysis of vibration and dynamic stability[J]. Journal of Huazhong University of Science & Technology: Urban Science, 2002, 19(1): 7-14.

[15] 曾庆元, 杨平. 形成矩阵的“对号入座”法则与桁梁空间分析的桁段有限元法[J]. 铁道学报, 1986, 8(2): 48-59.
ZENG Qing-yuan, YANG Ping. The “set-in-right-position” rule for forming structural matrices and the finite truss element method for space analysis of truss bridge[J]. Journal of the China Railway Society, 1986, 8(2): 48-59.

收稿日期：2009-01-08；修回日期：2009-03-25

基金项目：国家重点基础研究发展规划(“973”计划)项目(2007CB714706)；国家自然科学基金资助项目(50678176，50908232)；教育部新世纪优秀人才支持计划项目(NCET-07-0866)

通信作者：赫丹(1981-)，男，河南确山人，博士研究生，从事列车-轨道系统振动研究；电话：13038300245；E-mail: hdpx8110@sina.com

(编辑 陈灿华)