缓冲结构对隧道口微气压波的影响

刘堂红，田红旗，梁习锋

(中南大学 交通运输工程学院 轨道交通安全教育部重点实验室， 湖南 长沙， 410075)

摘  要：为有效缓解微气压波对隧道周围环境的影响，设置合理的缓冲结构，采用数值模拟计算和动模型模拟实验相结合的方法，对列车通过隧道引发的压力变化、微气压波和不同形式的缓冲结构进行研究。研究结果表明：对任一类型缓冲结构，其结构长度和入口断面积之间均存在固定的最佳匹配关系，即对断面扩大无开口型缓冲结构，当缓冲结构长度分别为1.0D，2.0D和3.0D(D为隧道等效直径)时，对应的最佳入口断面积分别为1.8S，1.9S和1.8S(S为隧道断面面积)，微气压波幅值分别减小46.7%，55.3%和52.8%；对线性喇叭型缓冲结构，当缓冲结构长度分别为1.5D，2.0D和3.0D时，对应的最佳入口断面积分别为2.5S，2.4S和2.7S，微气压波幅值分别减小59.4%，64.2%和71.6%。

关键词：列车；隧道；微气压波；缓冲结构

中图分类号：U451.3；U292.91          文献标识码：A         文章编号：1672-7207(2009)05-1306-06

Influence of hood on micro-pressure wave

LIU Tang-hong, TIAN Hong-qi, LIANG Xi-feng

(Key Laboratory of Traffic Safety on Track, Ministry of Education, School of Traffic & Transportation Engineering,

Central South University, Changsha 410075, China)

Abstract: In order to alleviate the influence of micro-pressure wave on environment nearby tunnel and design the reasonable hoods, pressure change, micro-pressure wave and a series of hoods were studied using numerical simulation and moving model experiment. The results show that there is an optimal matching relationship between the length and the area for each kind of hood. For the enlarged transect windowless hood, when the length is 1.0D, 2.0D and 3.0D (D is tunnel’s diameter), the corresponding most reasonable area is 1.8S, 1.9S and 1.8S (S is tunnel’s transverse area), and the amplitude of the micro-pressure wave decreases by 46.7%, 55.3% and 52.8%, respectively. For the horn hood, when the length is 1.5D, 2.0D and 3.0D, the corresponding most reasonable area is 2.5S, 2.4S and 2.7S, and the amplitude of the micro-pressure wave decreases by 59.4%, 64.2% and 71.6%, respectively.

Key words: train; tunnel; micro-pressure wave; hood

高速列车进入隧道引发以音速传播的压缩波到达隧道出口时，突然膨胀，形成脉冲波，其结果可能导致周围房舍窗玻璃破损，还有可能产生强烈的爆破声，这种脉冲波称为“微气压波”^[1-4]，其幅值与压缩波首波峰值及压力梯度有关，并大致与压力梯度成正比，而在阻塞比一定的条件下，压缩波首波峰值和压力梯度分别与列车运行速度的平方和立方近似成正比，故减小微气压波幅值，需降低压缩波首波峰值，减小其压力梯度，其中减小压力梯度的效果更明显^[5-8]。缓冲结构的作用是减小列车从进入隧道起始即形成的压缩波的压力梯度，从而减小微气压波幅值。缓冲结构的形式多种多样，主要包括断面扩大无开口型、线性喇叭型、二次函数型、断面扩大开口型、等断面开口型、不连续型和斜口型等类型。根据隧道洞口微气压波幅值，需对以下2种情况设置缓冲结构：

a. 在距洞口外50 m内无建筑物，当20 m处的微气压波幅值大于50 Pa时，应设置洞口缓冲结构；

b. 当距洞口50 m内有建筑物，建筑物处的微气压波幅值大于20 Pa时，应设置洞口缓冲结构。当建筑物对环境有特殊要求时，相应的微气压波幅值基准按要求确定^[9-13]。至于采用何种形式的缓冲结构，应根据隧道出口微气压波幅值、所在位置地理条件及建造成本等各种因素，进行综合分析经比较后选定。为此，必须通过研究，掌握列车通过隧道引发隧道出口处的微气压波规律。

1  数值模拟计算

1.1  计算模型、网格及边界条件

这里选用25型单层客车编组列车以160 km/h通过设有缓冲结构、长度为500 m的59 m²单线隧道作为计算对象，对各种缓冲结构的长度、面积、角度以及开口面积影响初始压缩波和微气压波的规律进行研究，其中，缓冲结构长度用L_h表示，缓冲结构断面积用S_h表示；隧道断面面积用S表示，隧道等效直径用D表示，对于59 m²隧道，其等效直径D为8.67 m；25型单层客车由df11型机车牵引，其断面面积S_c=12.45 m²，对应阻塞比(机车断面面积/隧道断面面积)β=0.211。这里对断面扩大无开口型和线形喇叭型 2种缓冲结构进行分析。缓冲结构网格如图1和图2所示。

图1  断面扩大型缓冲结构网格图

Fig.1  Grid of enlarged transect hood

图2  线性喇叭型缓冲结构网格图

Fig.2  Gid of linear horn hood

对于列车表面，给定运动边界条件，其X方向速度分量等于给定的列车运行速度v，Y和Z向速度分量为0；对流域两侧面、顶面、底面，给定无滑移边界条件。进口边界条件是相对压强p_in=0 Pa；出口边界条件是相对压强p_out=0 Pa；隧道壁面采用标准壁面函数模拟。

1.2  断面扩大无开口型缓冲结构计算结果

图3所示为L_h=2.0D时，断面扩大无开口型缓冲结构在入口断面面积不同时距隧道入口40 m处的初始压缩波曲线；图4所示为L_h=1.0D，2.0D和3.0D时，距隧道出口20 m处的微气压波幅值随缓冲结构入口断面面积的变化曲线；表1~3所示为L_h分别为1.0D，2.0D和3.0D，入口断面积不同时，距隧道出口20 m的微气压波幅值计算结果。

入口断面积：1—1.0S; 2—2.0S; 3—3.0S

图3  缓冲结构入口断面积对初始压缩波的影响

Fig.3  Effects of enlarged transect hood entrance section area on initial compression wave

缓冲结构长度：1—1.0D; 2—2.0D; 3—3.0D

图4  缓冲结构入口断面积对微气压波幅值的影响

Fig.4  Effects of enlarged transect hood entrance section area on amplitude of micro-pressure wave

表1  当L_h=1.0D时断面扩大型缓冲结构不同入口断面积微气压波计算结果

Table 1  Calculation results of amplitude of micro-pressure waves under L_h=1.0D for enlarged transect hood

表2  当L_h=2.0D时断面扩大型缓冲结构不同入口断面积微气压波幅值计算结果

Table 2  Calculation results of amplitude of micro-pressure waves under L_h=2.0D for enlarged transect hood

表3  当L_h=3.0D时断面扩大型缓冲结构不同入口断面积微气压波幅值计算结果

Table 3  Calculation results of amplitude of micro-pressure waves under L_h=3.0D for enlarged transect hood

由图3可见，列车在驶入缓冲结构瞬间即会形成压缩波，也就是说，有缓冲结构时的压力上升时间相对于无缓冲结构时的压力上升时间明显提前，但由于断面扩大型缓冲结构尾端与隧道入口的断面积有一突变，在缓冲结构入口形成压缩波，传播到此会发生反射、回传。因此，初始压缩波的压力上升分为2个阶段：第1阶段是列车进入缓冲结构瞬间形成，当列车头部驶入一段距离后，压力变化逐渐趋于平缓，这一平缓过程的时间随缓冲结构长度增大而增加；第2阶段为列车头部在进入主隧道瞬间产生。但3种长度的缓冲结构压力变化曲线峰值出现的时刻及大小均与未设置缓冲结构的隧道基本一致，表明缓冲结构对改变压缩波首波峰值的效果并不明显。

由图4可知，当缓冲结构长度L_h=1.0D时，入口断面积S_h=1.8S的微气压波幅值减小效果最好，微气压波幅值减小46.7%；当L_h=2.0D时，入口断面积S_h=1.9S的微气压波幅值减小效果最好，微气压波幅值减小55.3%；当L_h=3.0D时，入口断面积S_h=1.8S的微气压波幅值减小效果最好，微气压波幅值减小52.8%。

根据上述计算结果进行比选，断面扩大无开口型缓冲结构的入口断面积定为1.8S，按此选择合适的缓冲结构长度，由1.0D，1.5D，2.0D，2.5D，3.0D，4.0D和5.0D这7种长度所得的微气压波幅值计算结果见表4。

表4  当S_h=1.8S时断面扩大型缓冲结构不同长度微气压波幅值计算结果

Table 4  Calculation results of amplitude of micro-pressure waves under S_h =1.8S for enlarged transect hood

由表4可知，当缓冲结构长度L_h≤2.0D时，初始压缩波有2个波段；随着缓冲结构长度的增加(L_h≥3.0D)，初始压缩波成为3个波段。这说明大面积缓冲结构形成的压缩波峰值低于在小面积主隧道形成的压缩波峰值，使形成压缩波的压力以分段上升。若缓冲结构太短，则2次形成的压缩波将合在一起，不存在平缓过渡阶段，因而不能减缓形成压缩波的压力梯度^[14]。

由表4可见，当入口断面积S_h=1.8S，结构长度L_h=1.5D时，微气压波幅值比无缓冲结构隧道降低51.5%，若增加缓冲结构长度，缓解效果并不明显提高。

1.3  线性喇叭型缓冲结构计算结果

图5所示为L_h=1.5D，线性喇叭型缓冲结构的入口断面面积不同时，距隧道入口40 m处的初始压缩波曲线；图6所示为L_h分别为1.5D，2.0D和3.0D时，距隧道出口20 m处的微气压波幅值随缓冲结构入口断面面积的变化曲线；表5~7所示是L_h分别为1.5D，.0D和3.0D，入口断面积不同时，距隧道出口20 m处的微气压波幅值计算结果。

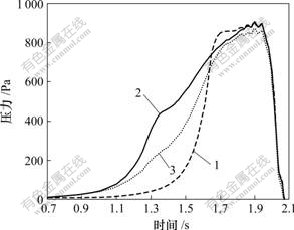
入口面积：1—1.0S; 2—2.0S; 3—3.0S

图5  喇叭型缓冲结构入口面积对初始压缩波的影响

Fig.5  Effects of linear horn hood entrance section area on initial compression waves

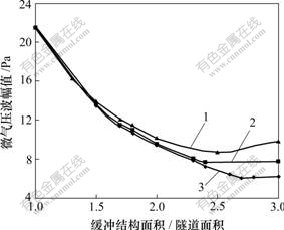
缓冲结构长度：1—1.0D; 2—2.0D; 3—3.0D

图6  喇叭型缓冲结构入口面积对微气压波的影响

Fig.6  Effects of linear horn hood entrance section area on micro-pressure waves

表5  当L_h=1.5D时喇叭型缓冲结构不同入口断面积微气压波幅值计算结果

Table 5  Calculation results of amplitude of micro-pressure wave under L_h=1.5D for linear horn hood

表6  当L_h=2.0D时喇叭型缓冲结构不同入口断面积微气压波幅值计算结果

Table 6  Calculation results of amplitude of micro-pressure wave under L_h=2.0D for linear horn hood

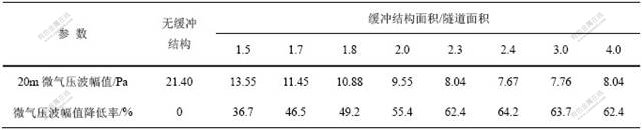
表7  当L_h=3.0D时喇叭型缓冲结构不同入口断面积微气压波幅值计算结果

Table 7  Calculation results of amplitude of micro-pressure wave under L_h=3.0D for linear horn hood

由上述计算结果可知，当线性喇叭型缓冲结构长度1.5D≤L_h≤2.0D，入口断面积S_h=1.8S时，微气压波幅值比无缓冲结构隧道降低46.9%~49.2%，其效果低于结构参数相同的断面扩大无开口型缓冲结构(51.5%~52.4%)。

断面扩大无开口型缓冲结构在L_h≤3.0D时，以L_h=2.0D，入口断面积S_h=1.9S时的气压波缓解效果最好，微气压波幅值减小55.3%，若再减小气压波幅值，就需在缓冲结构上设置开口。而对于线性喇叭型缓冲结构，要在该长度范围进一步降低微气压波幅值，可以通过适当扩大缓冲结构入口断面积实现，当L_h=1.5D，S_h=2.5S时，微气压波幅值减小59.4%；当L_h=2.0D，S_h=2.4S时，微气压波幅值减小64.2%；当L_h=3.0D，S_h=2.7S时，微气压波幅值减小71.6%。

2  动模型模拟实验

本实验室的列车气动性能模拟动模型实验装置，是国内唯一能对具有相对运动的列车交会和列车过隧道空气动力问题进行模拟实验研究的专用大型动模型试验设备^[15]。本次动模型模拟实验的模型缩尺比例为1?17.6，与数值计算相同，采用25型单层客车编组列车以160 km/h通过设置有缓冲结构的59 m²单线隧道。动模型实验与数值计算结果见表8。

表8  微气压波幅值动模型实验和数值计算结果

Table 8  Micro-pressure wave results of moving model experiment and numerical calculation

由表8可见，动模型模拟实验与数值计算结果比较接近，说明三维数值计算短隧道的微气压波具有较高的准度，但以往的研究表明，三维数值计算由于存在数值耗散等，长隧道的微气压波计算值明显偏小；另外，对于不同道床形式下微气压波随隧道长度的变化，目前的三维数值计算很难准确模拟，有待于进一步研究。

3  结  论

a. 对于断面扩大无开口型缓冲结构，当缓冲结构长度L_h=1.0D时，入口断面积S_h=1.8S的微气压波幅值减少最大，幅值减小达46.7%；当L_h=2.0D时，S_h=1.9S的微气压波幅值减少最大，幅值减小55.3%；当L_h=3.0D时，S_h=1.8S的微气压波幅值减少最大，幅值减小52.8%。当入口断面积S_h=1.8S时，结构长度L_h=1.5D的微气压波幅值比无缓冲结构时降低51.5%，若再增加长度，微气压波幅值减少效果改变不明显。

b. 对于线性喇叭型缓冲结构，当缓冲结构长度L_h=1.5D时，入口断面积S_h=2.5S的微气压波幅值减少最大，幅值减小59.4%；当L_h=2.0D时，S_h=2.4S的微气压波幅值减少最大，幅值减小64.2%；L_h=3.0D时，S_h=2.7S微气压波幅值减少最大，幅值减小71.6%。

参考文献：

[1] Aoki T. Passive alleviation of micro-pressure waves from tunnel portals[J]. Journal of Sound and Vibration, 1999, 220(5): 921-940.

[2] Raghunathan S, Kim H D, Setoguchi T. Aerodynamics of high-speed railway train[J]. Progress in Aerospace Sciences, 2002, 38(6): 469-514.

[3] Marc B, Bruno A, Tadashi K. Blind hood effects on the compression wave generated by a train entering a tunnel[J]. Experimental Thermal and Fluid Science, 2001, 25(6): 397-407.

[4] 韩 锟, 田红旗. 客运专线隧道空气动力学实车测试技术的应用与应用[J]. 中南大学学报: 自然科学版, 2007, 38(2): 326-332.
HAN Kun, TIAN Hong-qi. Research and application of testing technology of aerodynamics at train tunnel entry on special passenger railway lines[J]. Journal of Central South University: Science and Technology, 2007, 38(2): 326-332.

[5] Takanobu O, Kozo F. Numerical investigation of three- dimensional compressible flows induced by a train moving into a tunnel[J]. Computers & Fluids, 1997, 26(6): 565-585.

[6] Howei M S. On the role of separation in compression wave generation by a train entering a tunnel hood with a window[J]. LMA Journal of Applied Mathematics, 2005, 70(3): 440-418.

[7] Bellenoue M, Moriniere V, Kageyama T. Experimental 3-D simulation of the compression wave due to train-tunnel entry[J]. Journal of Fluids and Structures, 2002, 16(5): 581-598.

[8] 耿 烽, 张 倩, 梅元贵. 缓冲结构减缓高速铁路隧道出口微压波数值比较[J]. 交通运输工程学报, 2006, 6(3): 18-22.
GENG Feng, ZHANG Qian, MEI Yuan-gui. Numerical value comparison of micro-pressure wave in reduction by using hoods at high-speed railway tunnel exit[J]. Journal of Traffic and Transportation Engineering, 2006, 6(3): 18-22.

[9] 赵文成, 高 波, 漆泰岳. 高速铁路隧道出口微压波及其主被动减缓措施[J]. 石家庄铁道学院学报, 2004, 17(3): 5-9.
ZHAO Wen-cheng, GAO Bo, QI Tai-yue. Micro-pressure wave around high-speed railway tunnel exit and active and passive method of reduction[J]. Journal of Shijiazhuang Railway Institute, 2004, 17(3): 5-9.

[10] 刘堂红, 田红旗, 金学松. 隧道空气动力学实车试验研究[J]. 空气动力学学报, 2008, 26(1): 42-46.
LIU Tang-hong, TIAN Hong-qi, JIN Xue-song. Experimental study of full-scale train on aerodynamics in tunnel[J]. Acat Aerodynamica Sinica, 2008, 26(1): 42-46.

[11] 赵文成, 高 波, 王英学, 等. 喇叭型隧道入口的空气动力学特性的试验研究[J]. 四川大学学报, 2004, 36(4): 22-25.
ZHAO Wen-cheng, GAO Bo, WANG Ying-xue, et al. Experimental investigation of aerodynamic characteristic of tunnel flaring portals[J]. Journal of Sichuan University, 2004, 36(4): 22-25.

[12] 刘堂红, 梁习锋, 卢执中, 等. 隧道洞口缓冲结构的设置条件和结构形式研究报告[R]. 长沙: 中南大学轨道交通安全教育部重点实验室, 2007.
LIU Tang-hong, LIANG Xi-feng, LU Zhi-zhong, et al. Research report of the setting conditions and structure parameters of the hoods[R]. Changsha: Key Laboratory of Traffic Safety on Track of Ministry of Education, Central South University, 2007.

[13] 田红旗. 中国列车空气动力学研究进展[J]. 交通运输工程学报, 2006, 6(1): 1-9.
TIAN Hong-qi. Study evolvement of train aerodynamics in China[J]. Journal of Traffic and Transportation Engineering, 2006, 6(1): 1-9.

[14] 梁习锋, 田红旗. 遂渝线隧道空气动力学实车试验研究报告[R]. 长沙: 中南大学轨道交通安全教育部重点实验室, 2005.
LIANG Xi-feng, TIAN Hong-qi. Research report of full-scale train test for aerodynamics in tunnel on SUI-YU railway line[R]. Changsha: Key Laboratory of Traffic Safety on Track of Ministry of Education, Central South University, 2005.

[15] 赵 勇, 唐国荣. 关于客运专线隧道设计与施工的几点意见[J]. 铁道标准设计, 2005, 49(6): 1-8.
ZHAO Yong, TANG Guo-rong. Points on tunnel design and construction of passenger dedicated line[J]. Railway Standard Design, 2005, 49(6): 1-8.

收稿日期：2008-10-08；修回日期：2008-12-25

基金项目：铁道部科技研究开发计划项目(2005G003)

通信作者：刘堂红(1976-)，男，湖南新化人，讲师，从事车辆结构与空气动力学研究；电话：0731-82655294；E-mail: lthjd@163.com