冷弯薄壁型钢自攻螺钉连接抗剪性能试验研究及数值分析Ⅱ:数值分析
卢林枫1, 2,张亚平1,方文琦3,杨东华4
(1. 长安大学 建筑工程学院,陕西 西安,710061;
2. 长安大学 交通行业重点实验室,陕西 西安,710061;
3. 新时代(西安)设计研究院有限公司,陕西 西安,710054;
4. 西部机场集团有限公司,陕西 西安,710075)
摘要:在试验研究的基础上,利用ANSYS有限元程序,选取合适的单元,通过建立面面接触及模拟实际试验的边界条件,对冷弯薄壁型钢自攻螺钉连接试件进行数值模拟分析,并在自攻螺钉连接破坏模式、荷载变形曲线和抗剪承载力方面与试验结果进行对比分析,验证数值模拟分析方法的可靠性。然后在试验数值模拟分析的基础上,在自攻螺钉直径、连接板件厚度、螺钉排列方式、螺钉个数及螺钉间距等方面,对冷弯薄壁型钢自攻连接件抗剪承载力进行分析,得出单钉连接件的抗剪承载力随螺钉直径的增加而提高;当单钉连接件以螺钉倾斜、连接板件翘起破坏时,其抗剪承载力随连接板件厚度的增加而提高;螺钉数目和螺钉间距是影响螺钉连接抗剪性能的最主要因素。依据参数分析的主要结果,对螺钉连接抗剪承载力的设计方法进行探讨,提出相应的计算方法及构造建议。
关键词:冷弯薄壁型钢;自攻自钻螺钉;抗剪承载力;数值分析
中图分类号:TU391 文献标志码:A 文章编号:1672-7207(2013)08-3493-10
Experimental investigation and numerical analysis on shear-bearing capacity for self-drilling screw connections of cold-formed thin-walled steel Ⅱ: Numerical analysis
LU Linfeng1, 2, ZHANG Yaping1, FANG Wenqi3, YANG Donghua4
(1. School of Civil Engineering, Chang’an University, Xi’an 710061, China;
2. Key of Laboratory Communications, Chang’an University, Xi’an 710061, China;
3. New era(Xi’an) Design Engineering Co., LTD, Xi’an 710054, China;
4. China West Airport Group, Xi’an 710075, China)
Abstract: Based on the previous experimental investigation and finite element program, a numerical analysis on self-drilling screw connections of cold-formed thin-walled steel was conducted by selecting appropriate elements, using face to face contact model and simulating the actual boundary conditions. Through comparing the numerical results of failure modes, load-deformation curves and shear-carrying capacity with those of experimental results, the feasibility of the numerical analysis method was verified. According to the numerical analysis, the influence of parameters such as the diameter of self-drilling screw, the thickness of connections, screw arrangements, and screw numbers and spacing was analyzed. It is found that the shear-carrying capacity of single screw connections increases with the increase of screw diameter, and it is also improved with the thickening of connections when single screw connections are in failure with screw inclining and connect plate titling. Screw numbers and spacing are the major factors to shearing property of screw connections. On the basis of parameter analysis, the design method of shear-carrying for screw connections is discussed, and the corresponding calculation method and constitution are suggested.
Key words: cold-formed thin-walled steel; self-drilling screw connection; shear-bearing capacity; numerical analysis
鉴于冷弯薄壁型钢自攻螺钉连接抗剪试验样本的局限性[1-3],很多学者采用数值分析的方法对冷弯薄壁型钢自攻螺钉的抗剪性能进行研究。Babalola等[4]采用数值分析方法与北美规范AISI[5]及Rogers等[6-7]提出的计算方法进行对比分析;Fan等[8-9]对静力剪切作用下的不同板厚单颗螺钉连接进行有限元模拟。Skiffner等[10]针对有预加应力的自攻螺钉连接的复杂结构,利用Adina软件进行有限元分析,为利用有限元模拟自攻螺钉连接提供了一种新的思路。陈娟婷[11]引入材料非线性与接触非线性对金属蒙皮结构自攻螺钉连接性能进行研究,给出自攻螺钉等厚连接常见的破坏模式和连接的P-Δ曲线。张雪丽等[12]利用ANSYS程序对自攻螺钉波峰连接的抗剪性能进行了有限元模拟分析,并与试验结果进行对比分析。本文作者采用ANSYS有限元分析软件对冷弯薄壁型钢自攻螺钉连接试验中的试件进行数值模拟分析,研究不同参数对冷弯薄壁型钢自攻螺钉抗剪承载能力的影响,并提出相应的计算方法和构造建议。
1 有限元模型
1.1 单元选取和材料本构关系
模型尺寸依据试验中冷弯薄壁型钢自攻螺钉连接件建立,连接板件及自攻螺钉均采用ANSYS10.0软件中的Soild45单元进行模拟,在连接区段内螺钉孔周围建立面-面接触,接触状态的接触单元和目标单元由ANSYS程序自动分配。
自攻螺钉连接件板材材料性能依据材性试验实际结果取值[3],厚板屈服强度f y=344.586 MPa,极限抗拉强度fu=448.787 MPa,泊松比v=0.3,弹性模量E=2.14×105 MPa;薄板屈服fy=373.832 MPa,极限抗拉强度fu=447.664 MPa,泊松比v=0.3,弹性模量E=2.06×105MPa;应力-应变曲线采用多线性随动强化本构模型。自攻螺钉的材料性能依据螺钉厂家提供的产品检验报告书,极限抗拉强度fu=505 MPa,泊松比v=0.3,弹性模量E=2.1×105 MPa,分析时也采用多线性随动强化本构模型。
1.2 边界约束和荷载施加
依据试验中的加载装置及边界约束条件,在有限元分析时,具体的边界约束条件为:连接件上端所有的节点坐标在X和Z方向的线位移Ux和Uz受到约束,连接件下端所有节点在坐标X,Y和Z方向的线位移Ux,Uy和Uz也受到约束,放松其他自由度;荷载施加方法为:首先将连接件上端所有节点的y方向位移耦合到一个节点上,然后在此节点上施加y方向位移荷载。
2 数值分析结果与试验结果的对比
2.1 破坏模式对比分析
2.1.1 厚板螺钉系列试件破坏模式对比分析
厚板单颗螺钉系列试件破坏模式对比情况如图1(a)和图1(b)所示。对LH系列试件进行有限元分析时,螺钉发生倾斜、连接区段板端出现翘起现象,最后螺钉被剪断(图1(a)),而试验时LH试件最后也发生此现象(图1(b)),两者吻合较好。
厚板多颗螺钉系列试件选取试件A4-L2-P2-3D为例说明,如图1(c)和图1(d)所示。有限元分析时z方向出现较大位移,最终出现螺钉倾斜、连接区段板端翘起的破坏模式(图1(c));试验中同样呈现出此破坏模式,且连接板件在连接区段内钉帽处出现了板件撕裂现象(图1(d)),两者吻合较好。
2.1.2 薄板螺钉系列试件破坏模式对比分析
薄板单颗系列试件破坏模式对比情况如图2(a)和图2(b)所示。LB系列试件数值分析结果最终出现螺钉倾斜和连接区段板端翘起的现象(图2(a)),与试验时试件的破坏模式(图2(b))吻合较好。
薄板多颗螺钉系列试件选取试B7-W3-N1-3D为例说明,如图2(c)和图2(d)所示。数值分析结果最终出现螺钉倾斜和连接区段板端翘起的破坏模式(图2(c)),且z方向发生较大位移,即连接板件翘起现象比较严重;试验中同样呈现出上述破坏模式(图2(d)),且连接板件也出现翘起变形,两者吻合较好。
综上所述,对于本文所研究的冷弯薄壁型钢自攻螺钉连接件,无论是厚板或薄板自攻自螺钉系列试件,数值分析结果的破坏模式和试验破坏模式比较一致,两者吻合较好。

图1 厚板系列试件数值分析结果与试验破坏模式对比
Fig. 1 Numerical results of series of slab connections compared with experimental results on failure mode

图2 薄板系列试件数值分析结果与试验破坏模式对比
Fig. 2 Numerical results of series of sheet connections compared with experimental results on failure mode
2.2 荷载-变形曲线对比分析
本文选取LH,LB,A2-L1-P2和B7-W3-N1系列试件试验荷载-变形曲线和数值模拟得到的荷载-变形对比情况为例说明,如图3所示。
由图3可知:试验荷载-变形曲线与数值分析的荷载-变形曲线的走势和形状基本相同,除薄板单颗LB系列试件误差较大外,其余试件吻合较好。加载初期数值分析的荷载-变形曲线的斜率与试验荷载-变形曲线的斜率基本一致。随着荷载的持续增加,在弹塑性阶段,数值分析结果荷载-变形曲线始终高于试验荷载-变形曲线,因为有限元模型未能计入加工误差和初始缺陷对试件的不利影响。
2.3 抗剪承载力对比分析
厚板系列部分试件的自攻螺钉连接件的试验抗剪承载力和数值分析结果见表1,薄板系列部分试件的自攻螺钉连接件的试验抗剪承载力和数值分析结果见表2。由表1和表2可知:大部分试件数值分析得到的抗剪承载力和试验抗剪承载力相差很小,误差基本在10%以内,个别试件误差比较大(如LB系列薄板单颗螺钉试件),主要是由于试件加工误差和初始缺陷较大影响了试件的抗剪承载能力,而数值分析未能考虑生产的不利影响。
表1 厚板系列部分连接试件极限抗剪承载力对比
Table 1 Comparison of ultimate shear-bearing capacity of part of thick plate connections

表2 薄板系列部分连接件极限抗剪承载力对比
Table 2 Comparison of ultimate shear-bearing capacity of part of sheet connections

综上,ANSYS有限元数值分析能较好模拟冷弯薄壁型钢自攻螺钉连接件抗剪承载力试验,除个别试件因加工误差等造成初始缺陷较大,使数值模拟结误差较大外,其他大部分试件的数值分析结果和试验结果吻合较好,说明本文利用有限元分析模型和数值分析方法基本可行。
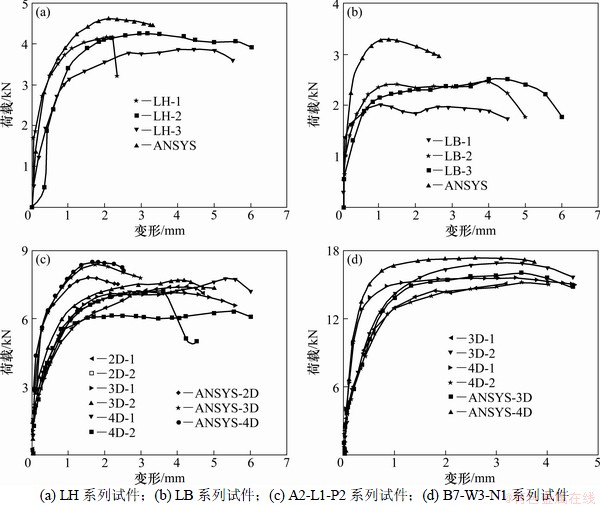
图3 试件荷载-变形曲线对比
Fig. 3 Comparison of connections load-deformation curve
3 影响因素分析
3.1 螺钉直径及连接板件厚度对单钉连接件抗剪承载力的影响
依据试验研究,并参考文献[13],分别取连接板件厚度t为0.45,0.6,0.75,0.8,1.0,1.2,1.4,1.6及1.8 mm;另根据常用自攻螺钉规格[14],分别取连接螺钉直径d为3.4,4.2,4.8,5.4及6.4 mm;建立等厚连接和不等厚连接(厚板厚度固定为1.8 mm,薄板厚度分别取上述连接板件厚度)的单钉连接件数值模型,对其抗剪承载力性能进行数值模拟。不同直径螺钉、不同板厚的单钉连接件数值分析结果对比曲线见图4。
由图4可知:对于单颗自攻螺钉连接件,无论是等厚还是不等厚连接,其抗剪承载力随连接螺钉直径增加而提高。通过统计连接的破坏模式和抗剪承载力之间的关系发现,当单钉连接件以螺钉倾斜、连接板件翘起为主破坏模式时,其抗剪承载力随连接板件厚度增加而提高,而当以螺钉被剪断破坏时,单钉连接件抗剪承载力不再随连接板件厚度的增加而变化。
3.2 螺钉排列方式对连接件抗剪承载力的影响
根据常用C形截面冷弯薄壁型钢形式,取连接板件(宽为89 mm,厚为1 mm)和连接螺钉(直径为4.2 mm)建立相同螺钉间距(取3倍螺钉直径)、不同排列方式的4颗和7颗螺钉连接件有限元模型,对其抗剪性能进行分析。不同排列方式的4颗螺钉连接件简图及编号见图5(a),不同排列方式的7颗螺钉连接件简图及编号见图5(b)。不同排列方式的4颗和7颗螺钉连接件的荷载-变形曲线对比结果见图6。
由图6可知:不同排列方式的4颗螺钉连接件最大极限抗剪承载力为16.411 kN(4-A试件),最小极限抗剪承载力为15.466 kN(4-D试件),其承载力最大增幅为6.11%,且其初始刚度、延性及破坏模式基本相同;不同排列方式的7颗螺钉连接件最大极限抗剪承载力为25.371 kN(7-A试件),最小极限抗剪承载力为23.345 kN(7-B试件),其承载力最大增幅为8.68%,且其初始刚度、延性及破坏模式也基本相同。综上所述,当连接螺钉数目及间距固定时,螺钉排列方式对自攻自钻螺钉连接件的抗剪承载力影响较小。

图4 不同直径螺钉和不同板厚的单钉连接件数值分析结果
Fig. 4 Numerical results of different diameters and thicknesses of single screw connection

图5 不同排列方式的4颗和7颗螺钉连接件简图
Fig. 5 Different arrangement of four and seven screw connections
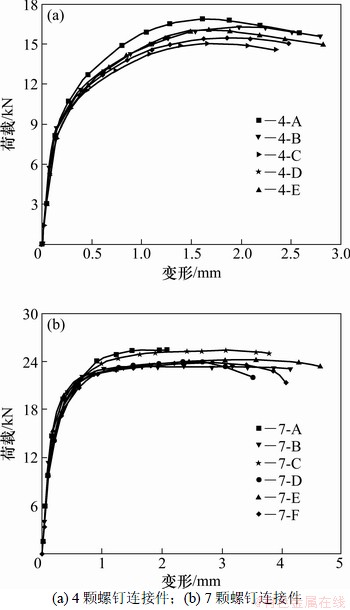
图6 不同排列方式自攻螺钉连接件荷载-变形曲线对比
Fig. 6 Comparison of different arrangement self-drilling connections load-deformation curve
3.3 螺钉个数对连接件抗剪承载力的影响
取连接板件(宽为89 mm,厚为1 mm)和连接螺钉(直径为4.2 mm),分别建立螺钉间距相同(取3倍螺钉直径)、螺钉个数不同的自攻螺钉连接件数值模型,对其抗剪性能进行分析。不同螺钉数目的螺钉连接件抗剪承载力对比结果见图7,螺钉数目对螺钉群效率系数的影响见图8。
由图7和图8可知:在螺钉间距固定的条件下,螺钉连接件抗剪承载力随螺钉个数的增加而提高,但不随螺钉个数成倍加大,而随螺钉个数的增加提高幅度逐渐减小,即螺钉群连接件具有“群体折减效应”;螺钉群的效率系数随螺钉个数的增加而逐渐减小(见图8),这说明螺钉群连接件中每颗螺钉的利用率随螺钉个数的增加而逐渐降低。
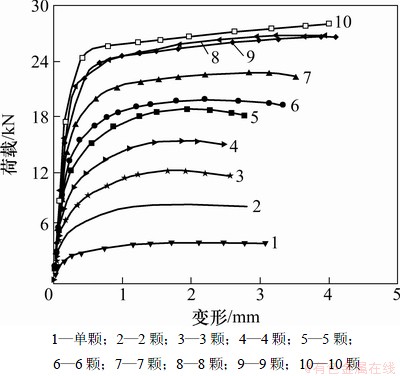
图7 不同螺钉数目的螺钉连接件抗剪承载力
Fig. 7 Different screw number connections shear capacity

图8 螺钉数目对螺钉群效率系数的影响
Fig. 8 Effect of screw number on screws group efficiency factor
3.4 螺钉间距对连接件抗剪承载力的影响
取连接板件(宽为89 mm,厚为1 mm)、连接螺钉(直径为4.2 mm),分别建立螺钉个数及排列方式相同(采用二排三列六颗螺钉连接)、螺钉间距不同(分别为2D,3D,4D,5D和6D,D为螺钉直径)的自攻螺钉连接件有限元模型,对其抗剪性能进行分析。螺钉间距对6颗螺钉连接件抗剪承载力的影响见图9,螺钉间距S对6颗螺钉群的效率系数的影响见图10。
由图9和图10可知:螺钉个数及排列方式相同时,自攻螺钉连接件的抗剪承载力及群体效应折减系数随螺钉间距的增大而非线性提高,提升幅度随螺钉间距增大而逐渐减小;当螺钉间距超过一定范围时,自攻螺钉连接件的抗剪承载力随增大螺钉间距提高幅度很小;另外,螺钉排列过于紧密时(S<3D,S为螺钉间距),根据试件数值分析破坏模式下的应力云图,发现自攻螺钉连接件板件翘起变形严重,不利于螺钉与板件共同工作,使连接件抗剪承载力过低,不能充分发挥其作用。
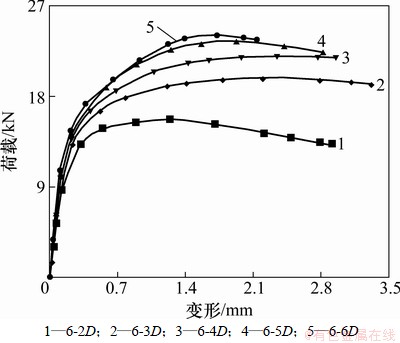
图9 不同螺钉间距的螺钉连接件抗剪承载力
Fig. 9 Different screw space connections shear capacity
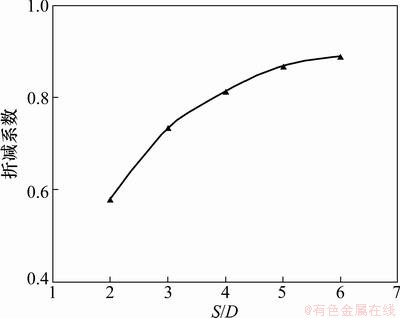
图10 螺钉间距对螺钉群效率系数的影响
Fig. 10 Effect of screw space on screws group efficiency factor
综上,当螺钉个数和排列方式相同时,在一定范围内(本文建议取:3D≤S≤5D),自攻螺钉连接件的抗剪承载力及群体效应折减系数随螺钉间距的增大而提高。
4 设计方法探讨
4.1 单颗自攻螺钉连接抗剪承载力设计方法
参考美国AISI规范[5],对我国GB 50018—2002规范[15]和文献[16]的设计方法进行修正,即补充螺钉剪断破坏模式下单钉连接件抗剪承载力的计算公式,具体形式为:
Pns=0.8Pss (1)
式中:Pns为单钉连接件发生螺钉剪断时抗剪承载力设计值;Pss为产品说明书给定的自攻螺钉名义抗剪承载力,由螺钉生产厂家通过试验测定。
采用式(1)分别计算GB 50018—2002规范和文献[16]单颗螺钉连接件的抗剪承载力修正值,并与北美AISI规范计算值和有限元计算结果(取3.1节的计算结果)进行对比分析,对比结果见图11。
由图11可知:考虑螺钉剪断破坏模式的修正方法,其计算结果和有限元分析结果相差不大,且偏于安全。另外,对比美国AISI规范、中国GB 50018—2002规范的修正法以及文献[16]的修正设计方法可知:采用美国AISI规范设计方法计算单钉连接件的抗剪承载力较为经济合理。因此,本文推荐采用北美AISI规范计算单颗冷弯薄壁型钢自攻螺钉连接件抗剪承载力。

图11 单颗螺钉连接件有限元值与修正方法计算值对比
Fig. 11 Single screw connection numerical results compared with correcting method calculation
4.2 自攻自钻螺钉群连接件抗剪承载力设计方法
中国GB 50018—2002规范和美国AISI规范均没有考虑自攻螺钉群连接件的“群体折减效应”,若按简单叠加办法来计算螺钉群连接件的承载能力,结果将偏于不安全。因此,本节在试验及数值分析的基础上,对螺钉群连接件的效率系数的计算公式进行回归,提出自攻螺钉群连接件抗剪承载力的建议设计方法。
依据3.3节研究结果,参考文献[16],对螺钉个数和螺钉群效率系数的关系(即n-R关系)进行回归分析,最终得到计算公式为:
R=0.626 6+0.373 4n-0.5 (2)
式中:R为自攻螺钉连接件群体效率系数;n为连接螺钉的颗数。
依据3.4节研究结果,对螺钉间距影响系数进行回归:以3D(D为螺钉直径)螺钉间距时的群体效应折减系数为基准,计算其他情况下的间距影响系数ξ,然后对S/D-ξ关系进行回归,得到螺钉间距影响系数ξ的计算公式为:
ξ=0.719(S/D)0.3 (3)
式中:ξ为螺钉间距影响系数;D为连接螺钉直径;S为连接螺钉间距(本文建议:3D≤S≤5D);
综上,本文建议自攻螺钉群连接件抗剪承载力的设计计算方法如下:
Pu=nRξPns且Pu≤An fu (4)
式中:Pu为自攻螺钉群连接件抗剪承载力;R为自攻螺钉群连接件群体效率系数,按式(2)计算;ξ为螺钉间距影响系数,按式(3)计算;An为连接板件净截面面积;n为连接螺钉个数;fu为连接板件抗拉强度设计值。Pns为单钉连接件抗剪承载力,按北美AISI规范计算,取下列3种情况下计算结果的最小值作为单钉连接件的抗剪承载力(2.03 mm≤d≤6.4 mm)。
情况一:当t2/t1≤1时:
 (5)
(5)
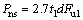 (6)
(6)
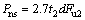 (7)
(7)
 (8)
(8)
其中:d为自攻螺钉直径;t1为与钉头接触的板件厚度;t2为不与钉头接触的板件厚度;Fu1为与钉头接触的板件抗拉强度;Fu2为不与钉头接触的板件抗拉强度;Pss为自攻螺钉名义抗剪承载力,由螺钉生产厂家通过试验测定。
情况二:当t2/t1≥2.5时:取式(6),(7)和(8)计算中的最小值。
情况三:当1<t2/t1<2.5时:Pns按以上2种情况线性插值得到。
另依据我国GB 50018—2002规范,自攻螺钉连接件的中距和端距不得小于3D;边距不得小于1.5D。
应用本文建议设计方法(式(4))计算自攻螺钉连接件的抗剪承载力,并将部分试件的计算结果与有限元变参数分析结果及试验结果进行对比(见表1和表2),式(4)的计算结果与试验结果比较吻合且偏于安全,说明式(4)建议的计算方法是合理可行的。
5 结论
(1) 单钉连接件的抗剪承载力随螺钉直径的增加而提高;当单钉连接件以螺钉被剪断为破坏模式时,单钉连接件的抗剪承载力相同,且不再随连接板件厚度的增加而变化;当其以螺钉倾斜、连接板件翘起破坏时,其抗剪承载力随连接板件厚度的增加而提高。
(2) 当螺钉数目及间距固定时,螺钉排列方式对自攻螺钉连接件的抗剪承载力影响较小。
(3) 螺钉个数是影响自攻自钻螺钉连接件抗剪承载力的主要因素之一,当螺钉间距固定时,自攻螺钉连接件的抗剪承载力随螺钉个数的增加而非线性提高,即螺钉群具有一定的群体折减效应。
(4) 螺钉间距是影响自攻螺钉连接件抗剪承载力的另一个主要因素,当螺钉个数和排列方式相同时,在一定范围内(3D≤S≤5D),自攻螺钉连接件的抗剪承载力及群体效应系数随螺钉间距的增大而非线性提高。
(5) 与试验数据和数值分析的对比分析结果表明,建议的计算方法合理可靠。
参考文献:
[1] Serrette R, Peyton D. Strength of screw connections in cold-formed steel construction[J]. Journal of Structural Engineering, 2009, 135(8): 951-958.
[2] 潘景龙. 自攻螺钉连接的抗剪性能研究[J]. 哈尔滨建筑大学学报, 1995, 28(6): 41-47.
PAN Jinglong. Research on self-drilling screws connection shear capacity[J]. Journal of Harbin University of Architecture, 1995, 28(6): 41-47.
[3] 方文琦. 冷弯薄壁型钢自攻自钻螺钉连接抗剪承载力性能研究[D]. 西安: 长安大学建筑工程学院, 2010: 12-38.
FANG Wenqi. Research on shear bearing capacity of cold-formed steel self-drilling screw connection[D]. Xi’an: Chang’an University. School of Civil Engineering, 2010: 12-38.
[4] Babalola M R, LaBoube R A. Strength of screw connections subject to shear force[R]. Rolla, Missouri: Department of Civil Engineering, Wei-Wen Yu Center for Cold-Formed Steel Structures, University of Missouri-Rolla, 2004.
[5] American Iron and Steel Institute, AISI. North American specification or the design of cold-formed steel structural members[S]. Washington, DC: American Iron and Steel Institute, 2001.
[6] Rogers C A, Hancock G J. Screwed connection tests of thin G550 and G300 sheet steels[R]. New South Wales, Australia: Centre for Advanced Structural Engineering, University of Sydney, 1997.
[7] Rogers C A, Hancock G J. Screwed connection tests of thin G550 and G300 sheet steels[J]. Journal of Structural Engineering, 1999, 125(2): 128-136.
[8] Fan L, Ronda l J, Cescotto S. Finite element model of single lap screw connections in steel sheeting under static shear[J]. Thin-Walled Structures, 1997, 27(2): 165-185.
[9] Fan L, Ronda l J, Cescotto S. Numerical simulation of lap screw connections[J]. Thin-Walled Structures, 1997, 29(1/2/3/4): 235-241.
[10] Skiffner K, Helling C D. Simulation of prestressed screw joints in complex structures[J]. Computers & Structures, 1997, 64(5/6): 995-1003.
[11] 陈娟婷. 金属蒙皮连接抗剪性能的分析研究[D]. 南京: 东南大学土木工程学院, 2006: 24-50.
CHEN Juanting. Analysis and study of metal skin connection shear capacity[D]. Nanjing: Southeast University. College of Civil Engineering, 2006: 24-50.
[12] 张雪丽, 张耀春. 基于ANSYS自攻螺钉波峰连接的抗剪性能有限元分析[J]. 建筑钢结构进展, 2010, 12(2): 23-29.
ZHANG Xueli, ZHANG Yaochun. Finite element analysis for shearing resistance of screw connections in crest-fixed profiled steel sheeting[J]. Progress of Construction Steel, 2010, 12(2): 23-29.
[13] Yu W W. Cold formed steel design[M]. 3rd Ed. New York: John Wiley & Sons Inc, 2000: 502-507.
[14] JGJ 227—2011, 低层冷弯薄壁型钢房屋建筑技术规程[S].
JGJ 227—2011, technical specification for low-rise cold-formed thin-wall steel buildings[S].
[15] GB 50018—2002,《冷弯薄壁型钢结构技术规范》[S].
GB 50018—2002, Technical code of cold-formed thin-wall structures[S].
[16] LaBoube R A, Sokol M A. Behavior of screw connections in residential construction[J]. Journal of Structural Engineering, 2002, 128(1): 115-118.
(编辑 何运斌)
收稿日期:2012-08-18;修回日期:2012-10-20
基金项目:陕西省自然科学基金资助项目(2007E225);中央高校基本科研专项基金资助项目(CHD2009JC008,CHD2012TD012);长安大学基础研究支持计划专项基金(2009);长安大学交通行业重点实验室开放基金资助(2009)
通信作者:卢林枫(1972-),男,黑龙江龙江人,博士,副教授,从事新型钢结构体系结构分析与设计研究;电话:029-82337821;E-mail:54LLF@163.com