DOI:10.19476/j.ysxb.1004.0609.2018.09.23
恒定水头条件下离子型稀土单井注液的影响范围
郭钟群1,赖远明2,赵 奎3,金解放1,王观石1
(1. 江西理工大学 建筑与测绘工程学院,赣州 341000;
2. 中国科学院 西北生态环境资源研究院,兰州 730000;
3. 江西理工大学 江西省矿业工程重点实验室,赣州 341000)
摘 要:在离子型稀土原地浸矿中,合理设置注液井网有利于提高资源回收率,计算井网参数的关键环节是确定单井注液影响范围,即湿润体特征及湿润锋运移规律。通过不同水头下稀土入渗试验可知,其湿润体形状近似为半椭球体,入渗初期横向湿润距离较垂向湿润距离大,随着入渗的进行,垂向湿润锋的发展速度较横向湿润锋的增大,湿润体形状由半椭球体向半球体发展。湿润体体积和累计入渗量之间存在显著的线性关系,表明湿润体内平均含水率增量基本上保持为一定值,横向和垂向最大湿润距离与入渗时间存在极显著的幂函数关系。基于Green-Ampt模型和水量平衡原理,建立了湿润体特征值计算模型,模型结果与试验结果吻合度较高,具有较高应用价值。根据三维Green-Ampt模型入渗能力曲线可知,随着时间的延长三维入渗率增加,这是三维入渗模型与一维入渗模型的显著区别。
关键词:恒定水头;离子型稀土;单井注液;计算模型
文章编号:1004-0609(2018)-09-1918-10 中图分类号:TD865 文献标志码:A
离子吸附型稀土(简称离子型稀土)是我国特有、世界关注的重要矿产资源,其中含有丰富的中重稀土,主要分布在江西、福建、广东、湖南、广西、云南、浙江等七省区[1-2]。在该类矿床中,稀土以水合阳离子或羟基水合阳离子形式吸附在黏土矿物上,具有配分齐全、高附加值元素含量高、放射性比度低、综合利用价值大等特点[3-5]。离子型稀土开采先后经历了池浸、堆浸和原地浸矿,目前主要采用原地浸矿的采矿方法[6-8],即直接在山体表面布置注液井网,注入盐类溶浸液渗透到黏土矿物中,通过离子交换过程将稀土离子交换于溶液中,浸出液通过山脚处的积液沟或收液巷道汇集到母液池,再通过沉淀母液中的稀土,实现资源回收。原地浸矿开采设计的关键因素是计算井网参数[9],如果注液井网布置太密,不仅增加注液井的钻孔工程量,且容易造成山体过度饱和,引起山体滑坡;如果注液井网布置太疏,则会形成许多浸矿死角与盲区, 从而影响稀土资源充分回收。设置井网参数的主要依据是单井注液影响范围,即入渗过程的湿润体特征及运移规律,因此,确定单井注液影响范围对于降低浸矿剂消耗、提高稀土资源回收率以及控制土体变形破坏具有重要意义。
关于土壤入渗的湿润体特征及渗流规律,国内外学者已进行了大量研究工作[10-13],SEPASKHAH等[14] 将三维Green-Ampt模型分析法用于推求地表入渗的湿润体半径和深度。毛丽丽等[15]基于改进Green-Ampt模型分析了入渗过程土中水含量变化规律。张振杰等[16]提出了黏壤土地表点源入渗的湿润体特征值经验解。赵伟霞等[17]定义了难以直接测定的概化湿润锋深度,建立了恒定水头井入渗模型。王文焰等[18]研究了黄土积水入渗的土壤水分剖面变化特征及入渗模型。尹升华等[19]通过变水头柱浸试验建立了入渗水头与入渗率的关系,推求了原地浸矿时最优入渗水头。
基于上述研究,取江西龙南足洞稀土矿区稀土进行三维入渗试验,研究了不同入渗水头下湿润体形状及湿润锋运移规律,推求了横向湿润锋距离、垂向距离与湿润体体积计算模型,并与试验值进行比较,检验模型精度,通过三维Green-Ampt模型入渗能力曲线分析了三维入渗率与一维入渗率的差异。
1 实验
1.1 试验装置
在文献[10]和文献[17]基础上进行实验装置设计,整个试验系统由供水瓶、试验土箱、注液井、溢流管、电子秤等组成,如图1所示。其中,注液井和土箱之间隔有纱布,防止土样进入注液井。根据单井注液的特点,试验土箱夹角为30°扇柱体土箱,土箱采用有机玻璃制作,垂直高度50 cm,径向长度50 cm,垂向和径向外壁上分别贴有刻度,注液井半径为1 cm。

图1 试验装置示意图
Fig. 1 Schematic diagram of experiment device
1.2 试验设计
试验土样取自江西龙南足洞矿区稀土,土样类别为黏质粉土。表1中,ρ为土样密度;θ为含水率;wl为液限;wp为塑限。将土样自然风干、捣碎、过筛,测得土样的基本物理参数见表1所示。按预定密度(1.56 g/cm3)将土样分层(5 cm)装入土箱内,每装入一层土样,用木锤轻轻将其均匀捣实,将捣实后的层面抓毛再装入下一层。入渗水头分别设置为5、10、15、20及25 cm,入渗时间要尽可能长,一般为8~10 h。
1.3 观测内容
注液开始后,用秒表计时,每隔10 min记录1次数据,按照先密后疏的原则观测土体湿润体水平方向和垂直方向上的入渗距离随时间的变化。由于所用风干土颜色较浅,水分湿润后的区域颜色明显清晰,因此可以在土箱上描绘出二维坐标系内不同入渗时刻所对应的湿润锋位置及形状,测量横向湿润距离、垂向湿润距离和15°、30°、45°、60°、75°方向的最大湿润距离。为了保证试验数据的准确性,每个水头入渗重复试验3次,取其平均值作为试验结果。通过观测供水瓶以及收液量筒中水量,便可求出土样中水的累计入渗量。
2 结果与分析
2.1 湿润体形状
单井注液的湿润体形状主要受土的质地和容重、水头高度、注液强度、注液时间和初始含水率等诸多因素的影响。湿润体形状是这些因素对土入渗能力和单孔注液强度的综合表现。为了方便观察湿润体,将实测的湿润体形状表示在二维坐标系内,如图2所示。由对称性可以看出,入渗的完整湿润体近似为半个椭球体。随入渗时间的延长,湿润体对称中心逐渐下移。分析认为,在入渗初期,土水势中主要是基质势作用在驱动湿润锋运移,水平方向上水分扩散速率快,土样湿润体的形状为长轴在横向的椭球体形状;随着入渗时间的延长,垂向的重力作用变大,重力势作用逐渐大于基质势,垂向的水分入渗速率相对增加,土样湿润体的形状开始向半球体发展。
考虑到一般情况,对湿润体形状是椭球体进行验证。假设土体湿润体为半个椭球体,且入渗点源在坐标系的中心,则过土体湿润体对称轴的任意剖面为一椭圆,该椭圆方程式为
 (1)
(1)
式中:a代表湿润体的横向最大湿润距离,cm;b代表湿润体的垂向最大湿润距离,cm。表2为某次试验(h=10 cm)中不同入渗时间不同观测角度上(湿润锋和入渗圆点与水平方向之间的角度)湿润锋与入渗圆点之间的径向距离观测结果。
表1 稀土试样的基本物理参数
Table 1 Basic physical parameters of ion-absorbed rare earth


图2 湿润体形状观测结果
Fig. 2 Results of wetting body shape
将10 min 实测的a=7.5 cm、b=5.5 cm 代入式 (1),即
 (2)
(2)
设此时刻湿润体过对称轴的纵剖面上15°角对应的湿润锋横向坐标为x,则垂向坐标y可表示为
y=tg15°·x=0.268x (3)
表2 不同入渗时刻湿润锋距离点源的径向距离
Table 2 Radial distances from wetting front and point source at different infiltration time

将式(3)代入式(2),得
 (4)
(4)
由式(4)解得x=7.0 cm,将x代入(2)可得y=1.9 cm,从而求得入渗10 min时湿润体剖面15°角对应的湿润锋距点源的径向距离(Ro)为
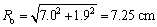 (5)
(5)
同理可求得30°、45°、60°、75°角湿润锋距离点源的距离分别为6.81、6.22、5.87和5.58 cm。依次计算30、60、180、420和600 min 湿润锋距离点源的距离,结果见表3。从表3可以看出,计算的距离和实测的距离有一定的差异,但其相对误差都保持在10%以内。依次分析入渗水头为5、15、20和25 cm的试验数据,与10 cm结果一致。综合分析,可以认为具有入渗水头的单井注液所形成的湿润体形状是半个椭球体。
以方程α=(a-b)/b计算椭球体扁率α。其中,a和b 为湿润体长半轴和短半轴的测量值,其值介于0和1之间,计算结果如图3所示。扁率反映了椭球体的扁平程度,α值愈大,椭球愈扁。分析可知,在入渗初始,湿润体扁率在0.3~0.4之间,随着入渗过程进行,湿润体扁率的逐渐减小,然后稳定在0.1左右,湿润体扁率的变化趋势也验证了随着入渗时间的增加,湿润体形状从半个椭球体逐渐向半球体发展。
2.2 湿润体体积和入渗时间、注液量的关系
通过上述湿润体形状分析可知,单井注液离子型稀土湿润体的形状接近于半个椭球体,因此,土壤湿润体的体积V(t)可以用椭球体体积公式计算:
 (6)
(6)
式中:A(t)为横向湿润距离;B(t)为垂向湿润距离。
掌握不同水头作用下,湿润体体积和入渗时间、累计入渗量之间的关系,无论是对离子型稀土原地浸矿的液井网设计还是注液量控制管理而言均具有重要的意义。用式(6)和试验数据计算不同入渗时刻的湿润体体积,其与累计入渗量的关系曲线如图4所示。由图4可以看出,在入渗量相同的条件下注液井内水头高度对于湿润体体积有一定影响,即供水量相同时,湿润体的体积随着注液水头的增加而减小。这也说明水头高度大时,湿润体的体积质量更大,含水率更高,饱和程度也更高,在一定程度上有利于离子型稀土原地浸矿的离子交换作用的发生。然而,相同累计入渗量的湿润体体积的差异不大,保持在10%以内。分析结果表明,湿润体体积V和累计入渗量W之间存在显著的线性关系,拟合方程为
W=0.326V,Rr=0.9774 (7)
式(7)表明土体湿润体内平均含水率增量基本上保持为一定值,即Δθ =0.326。设干土层的含水率为初始含水率θi,湿润体内的稳定含水率为饱和含水率θs,则Δθ=θs-θi=0.326。此处含水率是体积含水率。
2.3 湿润锋距离与入渗时间的经验关系
掌握不同水头入渗过程中土的湿润体特征值与入渗时间关系,是确定工程实践中注液井网参数的重要依据。恒定水头入渗的水平湿润距离A(t)和垂向入渗深度B(t)是湿润体二个重要的特征值,其入渗距离与时间关系曲线如图5和6所示。
表3 湿润锋实测值与计算值的误差分析
Table 3 Error analysis of measurement and calculation for wetting front


图3 湿润体扁率随时间的变化
Fig. 3 Change of oblateness of wetted volume with time
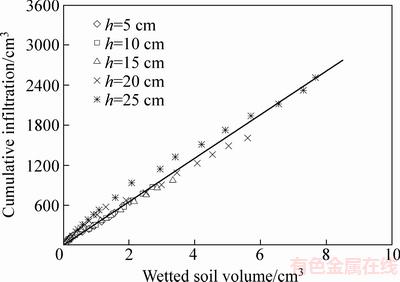
图4 湿润体体积与累计入渗量的关系
Fig. 4 Relationship between wetted soil volume and cumulative infiltration
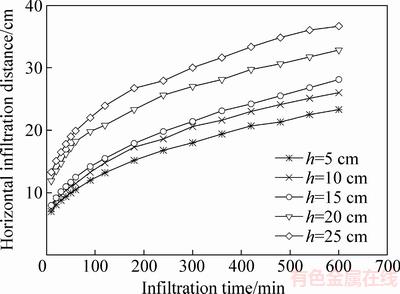
图5 入渗水头对水平湿润锋的影响
Fig. 5 Effect of infiltration head on horizontal wetting front
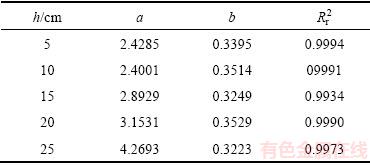
对横向入渗距离A(t)和垂向入渗距离 B(t)与时间t的关系,采用幂函数、指数函数和对数函数进行回归分析,结果表明,幂函数能够比较精确地描述横向和垂向入渗距离与时间的关系,相关系数的平方值 均在0.99以上。幂函数形式为:A(t)=atb;B(t)=ctd,a、b、c、d为湿润锋距离和入渗时间关系的拟合参数,二者通过湿润锋的观测易于获得,拟合结果见表4和5,利用该函数能够显著的表示湿润锋的运移规律。
均在0.99以上。幂函数形式为:A(t)=atb;B(t)=ctd,a、b、c、d为湿润锋距离和入渗时间关系的拟合参数,二者通过湿润锋的观测易于获得,拟合结果见表4和5,利用该函数能够显著的表示湿润锋的运移规律。

图6 入渗水头对垂向湿润锋的影响
Fig. 6 Effect of infiltration head on vertical wetting front
表4 水平湿润锋和入渗时间关系拟合结果
Table 4 Fitting results of relationship between horizontal wetting front and duration of infiltration

表5 垂向湿润锋和入渗时间关系拟合结果
Table 5 Results of fitting of relationship between vertical wetting front and duration of infiltration
3 计算模型
3.1 湿润体半径
通过试验可知,离子型稀土单井注液的影响范围是一个椭球体。基本假设如下:1) 注液井在椭球的中心,且初始时刻(t=0)供水源半径等于注液井半径。2) 注液过程中,湿润体内部是饱和区,土中含水率为饱和含水率,渗透系数为饱和渗透系数,湿润体外部是干燥区,土中含水率为初始含水率[20]。3) 土中毛管势忽略不计。4) 水分运动和湿润锋运移是从椭球中心沿着径向往四周扩散[21]。在湿润峰上取楔形微元da,如图7所示,则有
 (8)
(8)
式中:da表示微元,量纲L2;R为湿润峰到椭球中心的径向距离,量纲L;θ为水平面与微元体的夹角,量纲为1。

图7 湿润体特征参数分析图
Fig. 7 Variables used to describe wetting pattern
由式(8)可知,所取微元da是湿润锋到椭球中心的径向距离平方R2的比例项,由质量守恒定理可知,通过微元da的水流通量与微元面积(湿润锋到椭球中心的径向距离平方的比例项)成反比。即
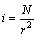 (9)
(9)
式中:i为入渗率(水流通量),量纲为L/T;N为比例系数,量纲为L3/T;r表示微元上任意点到椭球中心的径向距离,量纲为L。
根据达西定律和Green-Ampt模型,水流通量可以表示为
 (10)
(10)
式中:K为饱和导水率,量纲为L/T;h为总水头,量纲为L。
联立式(9)和(10)可得
 (11)
(11)
整理后,得
 (12)
(12)
两边积分,得
 (13)
(13)
式中:r0为注液井半径,量纲为L;H为水头高度,量纲为L。
求解式(13)可得
 (14)
(14)
把式(14)代入式(9),可得
 (15)
(15)
当r=R时,湿润锋边界处的水流通量为
 (16)
(16)
由水量平衡原理和Green- Ampt入渗模型中的假定得到t时间内入渗量I和土体湿润锋推进距离之间R的关系:
 (17)
(17)
式中:I为累计入渗量,量纲为L3;θi为土体初始含水率,量纲为1;θs为土体饱和含水率,量纲为1。
入渗率和累计入渗量之间的转换关系如下:
 (18)
(18)
式(18)表明,任意时刻的入渗率等于时段内累计入渗量对时间的导数,且等于土体湿润前后含水率变化值与湿润锋推进速度的乘积。因此通过试验记录土体湿润锋推进过程就可以计算得到土的入渗性能曲线。
由式(16)和(18)可得
 (19)
(19)
重新整理式(19),可得
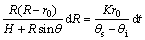 (20)
(20)
对式(20)进行积分,得
 (21)
(21)
求解式(21),得
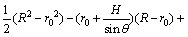

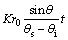 (22)
(22)
当sinθ=0时,R为湿润体横向最大湿润距离,用Ra表示,由式(20)得
 (23)
(23)
对式(23)积分可得
 (24)
(24)
当sin θ=1时,R为湿润体垂向最大湿润深度,用Rb表示,可得

 (25)
(25)
由式(24)和(25)可以得到时间t与横向最大湿润距离、垂向最大湿润深度之间的关系。
若已知注液井半径、注液水头高度、初始含水率、饱和含水率、饱和渗透系数等参数,则可得到湿润锋距离R与时间t的关系曲线,如图8所示。由图8可看出,曲线的斜率在入渗初期比较大,随后趋于平缓。这是由于在三维入渗中,水在土中渗透是向四周扩散,入渗初期湿润体体积小,渗透阻力小,随着湿润体体积越来越大,湿润体周围的渗透阻力逐渐增大,且小于基质吸力的增加量,故湿润锋推进的速度逐渐减小。
代入相应数据,利用Matlab软件编程可以得到模型的计算值,湿润距离计算值与实测值的关系曲线如图9所示。由图9可知,当用直线方程拟合不同入渗水头的湿润锋距离计算值与实测值曲线时,相关系数为 =0.9660,直线斜率为0.9906。说明二者具有较好的吻合度,即该计算模型具有很好的适用性。当实验室测得R和t时,由式(24)和(25)也可以反演饱和渗透系数,亦可以作为渗透系数计算与验证的一种方法。
=0.9660,直线斜率为0.9906。说明二者具有较好的吻合度,即该计算模型具有很好的适用性。当实验室测得R和t时,由式(24)和(25)也可以反演饱和渗透系数,亦可以作为渗透系数计算与验证的一种方法。

图8 湿润锋距离与时间的关系曲线
Fig. 8 Relationship between wetting front distance and time

图9 横向湿润锋计算值与实测值
Fig. 9 Calculated and measured values of horizontal wetting front
3.2 湿润体体积
湿润体体积是另外一个重要的特征值[22],图7中所取楔形微元体的体积可以由棱柱体公式求得,即
 (26)
(26)
湿润体的体积可以表示为
 (27)
(27)
式(25)是一个以时间为变量的隐函数,在实际中不方便应用与计算,可以运用数值反演的方法,把V和t的关系用图形呈现,如图10所示[21]。

图10 三维Green-Ampt模型入渗能力曲线
Fig. 10 Infiltration capacity curves of three-dimensional Green-Ampt model
为了减少式(26)中变量的数量,先对式(22)进行无量纲化处理,两边除以r02可得

 (28)
(28)
由此可知,R/r0是H/r0、θ和Kt/[r0(θs-θi)]的函数
 (29)
(29)
式中:f (R)是一个关于R的隐函数,把式(29)代入式(27),进行无量纲处理,可得到
 (30)
(30)
由于θ是这个积分的一个虚拟变量(哑变量),故式(30)可以变成
 (31)
(31)
式中:g(V)是一个关于(V)的隐函数,式(31)中的三维变量被用来计算V和t之间的几何关系。
图10所示为三维Green-Ampt模型入渗能力曲线。由图10可以看出,当入渗时间较长的情况下,即当Kt/r0(θs-θi)>10,直线的斜率均大于1,说明入渗率随着时间的增加而增加,也是三维入渗模型与一维模型最显著的差异。显然,充足供水条件下,随着湿润锋推移,湿润体的体积增量对入渗率的影响比水力梯度减少量对入渗率的影响要更大。
4 结论
1) 通过不同的恒定水头条件下稀土入渗试验可知,其湿润体形状近似为半椭球体,入渗初期横向湿润距离较垂向湿润距离大,随着入渗的进行,垂向湿润锋较横向湿润锋的发展速度增大,湿润体形状由半椭球体向半球体发展。
2) 湿润体体积和累计入渗量之间存在显著的线性关系,说明土体湿润体内平均含水率增量基本上保持为一定值;横向和垂向最大湿润距离与入渗时间存在极显著的幂函数关系。
3) 基于Green-Ampt模型和水量平衡原理,建立了湿润体特征值计算模型,模型结果与试验结果吻合度较高,具有应用价值。根据三维Green-Ampt模型入渗能力曲线,说明三维入渗率随着时间的增加而增加,这是三维入渗模型与一维模型最显著的差异。
REFERENCES
[1] 池汝安, 田 君. 风化壳淋积型稀土矿评述[J]. 中国稀土学报, 2007, 25(6): 641-650.
CHI Ru-an, TIAN Jun. Review of weathered crust rare earth ore[J]. Journal of the Chinese Rare Earth Society, 2007, 25(6): 641-650.
[2] 郭钟群, 金解放, 赵 奎, 王晓军, 陈国梁. 离子吸附型稀土开采工艺与理论研究现状[J]. 稀土, 2018, 39(1): 132-141.
GUO Zhong-qun, JIN Jie-fang, ZHAO Kui, WANG Xiao-jun, CHEN Guo-liang. Status of leaching technology and theory of ion adsorption type rare earth ores[J]. Chinese Rare Earths, 2018, 39(1): 132-141.
[3] HUANG Xiao-wei, LONG Zhi-qi, LI Hong-wei. Development of rare earth hydrometallurgy technology in China [J]. Journal of Rare Earths, 2005, 23(1): 1-4.
[4] 饶振华, 武立群, 袁源明. 离子型稀土发现、命名与提取工艺发明大解密[J]. 中国金属通报, 2007(29): 8-15.
RAO Zhen-hua, WU Li-qun, YUAN Yuan-min. Ion type rare earth discovery, naming and extraction technology invention decryption [J]. China Metal Bulletin, 2007(29): 8-15.
[5] 李永绣, 周新木, 刘艳珠, 李东平, 李 静, 唐 群. 离子吸附型稀土高效提取和分离技术进展[J]. 中国稀土学报, 2012, 30(3): 258-264.
LI Yong-xiu, ZHOU Xin-mu, LIU Yan-zhu, LI Dong-ping, LI Jing, TANG Qun. Development of high efficiency extraction and separation technologies of rare earths from ion-adsorbed type deposit[J]. Journal of the Chinese Rare Earth Society, 2012, 30(3): 258-264.
[6] 丁嘉榆. 离子型稀土矿开发的历史回顾—纪念赣州有色冶金研究所建所60周年[J]. 有色金属科学与工程, 2012, 3(4): 14-19.
DING Jia-yu. Historical review of the ionic rare earth mining: In honor of the 60 anniversary of GNMRI[J]. Nonferrous Metals Science and Engineering, 2012, 3(4): 14-19.
[7] 程建忠, 车丽萍. 中国稀土资源开采现状及发展趋势[J]. 稀土, 2010, 31(2): 65-69.
CHENG Jian-zhong, CHE Li-ping. Current mining situation and potential development of rare earth in China[J]. Chinese Rare Earths, 2010, 31(2): 65-69.
[8] YANG Xiu-li, ZHANG Jun-wei. Recovery of rare earth from ion-adsorption rare earth ores with a compound lixiviant[J]. Separation and Purification Technology, 2015, 142: 203-208.
[9] 王观石, 邓 旭, 胡世丽, 洪本根, 罗嗣海. 非达西渗流条件下的单孔注液强度计算模型[J]. 矿冶工程, 2015, 35(3): 4-8.
WANG Guan-shi, DENG Xu, HU Shi-li, HONG Ben-gen, LUO Si-hai. A calculation model for intensity of single-hole liquid injection under Non-Darcy flow condition[J]. Mining and Metallurgical Engineering, 2015, 35(3): 4-8.
[10] 汪志荣, 王文焰, 王全九, 张建丰. 点源入渗土壤水分运动规律实验研究[J]. 水利学报, 2000, 30(6): 39-44.
WANG Zhi-rong, WANG Wen-yan, WANG Quan-Jiu, ZHANG Jian-feng. Experimental study on soil water movement from a point source[J]. Journal of Hydraulic Engineering, 2000, 30(6): 39-44.
[11] 王路珍, 陈占清, 孔海陵, 倪晓燕. 渗透压力和初始孔隙度对破碎泥岩变质量渗流影响的试验研究[J]. 采矿与安全工程学报, 2014, 31(3): 462-468.
WANG Lu-zhen, CHEN Zhan-qing, KONG Hai-ling, NI Xiao-yan. An experimental study of the influence of seepage pressure and initial porosity on variable mass seepage for broken mudstone[J]. Journal of Mining & Safety Engineering, 2014, 31(3): 462-468.
[12] 吴爱祥, 尹升华, 李建锋. 离子型稀土矿原地溶浸溶浸液渗流规律的影响因素[J]. 中南大学学报(自然科学版), 2005, 36(3): 506-510.
WU Ai-xiang, YIN Shen-hua, LI Jian-feng. Influential factors of permeability rule of leaching solution in ion- absorbed rare earth deposits with in-situ leaching[J]. Journal of Central South University(Science and Technology), 2005, 36(3): 506-510.
[13] 丁德馨, 李广悦, 徐文平, 张志军, 饶 龙. 松散破碎介质中液体饱和渗流规律研究[J]. 岩土工程学报, 2010, 32(2): 180-184.
DING De-xin, LI Guang-yue, XU Wen-ping, ZHANG Zhi-jun, RAO Long. Regularities for saturated water seepage in loose fragmented medium[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(2): 180-184.
[14] SEPASKHAH A R, CHITSAZ H. Validating the Green-Ampt analysis of wetted radius and depth in trickle irrigation[J]. Biosystem Engineering, 2004, 89(2): 231-236.
[15] MAO Li-li, LI Yu-Zhong, HAO Wei-ping, ZHOU Xiao-ni, XU Chun-ying. A new method to estimate soil water infiltration based on a modified Green-Ampt model[J]. Soil and Tillage Research, 2016, 161(3): 31-37.
[16] 张振华, 蔡焕杰, 杨润亚. 地表滴灌土壤湿润体特征值的经验解[J]. 土壤学报, 2004, 41(6): 870-875.
ZHANG Zhen-hua, CAI Huan-jie, YANG Run-ya. An empirical solution of characteristic values of wetted solum under surface drip irrigation[J]. Acta Pedologica Sinica, 2004, 41(6): 870-875.
[17] 赵伟霞, 张振华, 蔡焕杰, 谢恒星. 恒定水头井入渗 Green -Ampt 模型的改进与验证[J]. 水利学报, 2010, 41(4): 464-470.
ZHAO Wei-xia, ZHANG Zhen-hua, CAI Huan-jie, XIE Heng-xing. Improvement and verification of the Green-Ampt model for constant-head well permeameter[J]. Journal of Hydraulic Engineering, 2010, 41(4): 464-470.
[18] 王文焰, 汪志荣, 王全九, 张建丰. 黄土中Green-Ampt入渗模型的改进与验证[J]. 水利学报, 2003, 35(1): 30-35.
WANG Wen-yan, WANG Zhi-rong, WANG Quan-jiu, ZHANG Jian-feng. Improvement and evaluation of the Green-Ampt model in loess soil[J]. Journal of Hydraulic Engineering, 2003, 35(1): 30-35.
[19] 尹升华, 谢芳芳. 基于 Green-Ampt 模型离子型稀土柱浸试验入渗水头的确定[J]. 中国有色金属学报, 2016, 26(12): 2668-2675.
YIN Sheng-hua, XIE Fang-fang. Infiltration head of ion-absorbed rare earth with column leaching experiment determined based on Green-Ampt model[J]. The Chinese Journal of Nonferrous Metals, 2016, 26(12): 2668-2675.
[20] GREEN W H, AMPT G A. Studies on soil physics: 1. Flow of air and water through soils[J]. Journal of Agricultural Science, 1911, 4(1): 1-24.
[21] CHU S T. Green-Ampt analysis of wetting patterns for surface emitters[J]. Irrigation and Drainage Engineer, 1994, 119(3): 443-456.
[22] 王成志, 杨培岭, 任树梅, 杨林林. 保水剂对滴灌土壤湿润体影响的室内实验研究[J]. 农业工程学报, 2006, 22(12): 1-7.
WANG Cheng-zhi, YANG Pei-ling, REN Shu-mei, YANG Lin-lin. Laboratory experiment on the effects of super absorbent polymer on wetting front of drip irrigation[J]. Transactions of the Chinese Society of Agricultural Engineering, 2006, 22(12): 1-7.
Influence range of single hole injection of ionic rare earth for constant head
GUO Zhong-qun1, LAI Yuan-ming2, ZHAO Kui3, JIN Jie-fang1, WANG Guan-shi1
(1. School of Architectural and Surveying and Mapping Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China;
2. Northwest Institute of Eco-Environmental and Resources, Chinese Academy of Sciences, Lanzhou 73000, China;
3. Jiangxi Key Laboratory of Mining Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China)
Abstract: Reasonable set of fluid injection wells of ion type rare earth in-situ leaching is conducive to improve the recovery rate of resources, and the key step in calculating parameters of wells is to determine effect range of single well injection, which means characteristics and migration laws of the moist body. It can be seen that the shape of moist body is approximately semi-ellipsoid through the infiltration experiments of rare earth under different heads. In the initial stage of infiltration, the transverse wetting distance is larger than that of vertical orientation, with infiltration, vertical development rate increases more quickly, and the shape of moist body develops from semi ellipsoid to hemisphere. The significant linear relationship between commulative infiltration and volume of moist body show that the increment of average moisture content nearly maintains a constant, moreover, there is an power function relationship between the horizontal and vertical maximum wetting distance and the infiltration time. The calculation model of the characteristic value of moist body was established based on the Green-Ampt model and the principle of water balance, and the results based on the calculation model fit well with that of experiments. According to the infiltration capacity curve of three-dimensional Green-Ampt model, it can be concluded that the three-dimensional infiltration rate increases with the increase of time, which is sharply distinctive from one-dimensional model.
Key words: constant-head; ion-absorbed rare earth; single hole injection; calculation model
Foundation item: Project(51664015) supported by the National Natural Science Foundation of China; Project (20151BAB206025) supported by the Jiangxi Natural Science Foundation, China; Project (YB2017002) supported by the Program for Excellent Doctor in Jiangxi University of Science and Technology, China
Received date: 2017-09-07; Accepted date: 2018-02-04
Corresponding author: GUO Zhong-qun; Tel: +86-797-8312551; E-mail: guozhongqun_jxust@163.com
(编辑 龙怀中)
基金项目:国家自然科学基金资助项目(51664015);江西省自然科学基金资助项目(20151BAB206025);江西理工大学优秀博士学位论文培育项目(YB2017002)
收稿日期:2017-09-07;修订日期:2018-02-04
通信作者:郭钟群,讲师,博士研究生;电话:0797-8312551;E-mail:guozhongqun_jxust@163.com