
DOI: 10.11817/j.issn.1672-7207.2020.07.024
考虑3种因素影响的硫氧镁水泥固化土修正邓肯-张模型
朱剑锋1, 2,徐日庆3, 4,罗战友1, 2,饶春义5
(1. 浙江科技学院 土木与建筑工程学院,浙江 杭州,310023;
2. 浙江科技学院 隧道与地下空间技术开发研究院,浙江 杭州,310023;
3. 浙江大学 滨海和城市岩土工程研究中心,浙江 杭州,310058;
4. 浙江加州国际纳米技术研究院台州分院,浙江 台州,318000;
5. 宁波大学 土木与环境工程学院,浙江 宁波,315211)
摘要:为了研究初始含水量(w)、固化剂掺量(Wg)和龄期(T)对硫氧镁水泥固化土力学特性的影响规律,开展不同初始含水量、固化剂掺量和龄期下硫氧镁水泥固化土的不排水三轴试验,并根据试验结果建立邓肯-张模型参数K,c,φ与w,Wg,T关系的经验公式,提出考虑初始含水量、固化剂掺量和龄期影响的硫氧镁水泥固化土的修正邓肯-张模型,通过算例分析验证修正模型的准确性。研究结果表明:硫氧镁水泥固化土的破坏形式主要分为侧向鼓胀破坏和斜向剪切破坏,应力-应变关系主要分为加工硬化型和软化型2种形式。随着初始含水量的减少、固化剂掺量的增大和龄期的增长,硫氧镁水泥固化土的强度和刚度(初始切线模量)显著提高,修正邓肯-张模型准确可靠。
关键词:硫氧镁水泥;固化土;初始含水量;固化剂掺量;龄期
中图分类号:TU472.5 文献标志码:A 开放科学(资源服务)标识码(OSID)
文章编号:1672-7207(2020)07-1989-13
Modified Duncan-Chang constitutive model for soft soil stabilized by magnesium oxysulfate cement considering three effect factors
ZHU Jianfeng1, 2, XU Riqing3, 4, LUO Zhanyou1, 2, RAO Chunyi5
(1. School of Civil Engineering and Architecture, Zhejiang University of Science and Technology,Hangzhou 310023, China;
2. Institute of Tunnel and Underground Space, Zhejiang University of Science and Technology,Hangzhou 310023, China;
3. Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University,Hangzhou 310058, China;
4. Zhejiang-California International Nano Systems Institute Taizhou Branch, Taizhou 318000, China;
5. School of Civil Environmental Engineering, Ningbo University, Ningbo 315211, China)
Abstract: To study the effects of initial water contents(w), curing agent dosages(Wg) and ages(T) on the mechanical properties of soft soil solidified by magnesium oxysulfate cement, a series of undrained triaxial tests were conducted on the cured soil with different initial water contents, curing agent dosages and ages. According to the experimental results, the empirical relationship between the Duncan-Chang model parameters such as K, c and φ and w, Wg and T was studied. Subsequently, the modified Duncan-Chang model of solidified soil considering initial water contents, curing agent dosages and ages was developed and proved to be accurate and reliable. The results show that the failure modes of solidified soil can be mainly divided into two models, lateral-bulging-failure model and oblique-shear-failure model. The stress-strain relationship mainly covers two different patterns, i. e.,strain hardening and strain softening. With the decrease of the water content and the increase of the curing agent dosage and the age, the strength and stiffness of solidified soil behave stronger. The modified Duncan-Chang model of solidified soil is accurate and reliable.
Key words: magnesium oxysulfate cement; solidified soil; initial water content; curing agent dosages; curing date
固化土的无侧限抗压强度主要受固化剂掺量、初始含水量、龄期等因素影响,人们对此开展了很多研究,例如:朱伟等[1]提出了水泥固化土无侧限抗压强度与水泥添加量之间的经验公式,但未考虑龄期的影响;董邑宁等[2]研究了掺入比、龄期对固化土强度的影响规律;KOLIAS等[3]分析了不同配比下固化土的无侧限抗压强度随龄期的演化规律。软土初始含水量也是影响软土加固效果的重要因素,HORPIBULSUK等[4]研究了固化淤泥质土无侧限抗压强度随含水量、水泥掺量和养护龄期的变化规律;徐日庆等[5]建立了考虑初始含水量、固化剂掺量等因素影响的固化土综合抗压强度预测模型;杨爱武等[6]基于无侧限抗压强度试验结果,分析了含水率、龄期、固化剂掺量对吹填泥浆固化土强度的影响规律。除了无侧限抗压度指标外,固化土的抗剪强度、变形特征以及它们之间的关系(本构关系)也逐渐引起了学者们的广泛关注。童小东等[7]结合水泥固化土的试验结果,提出了水泥土的损伤理论模型;王军等[8]根据不排水三轴试验建立了考虑水泥土刚度软化的固化土模型;张涛等[9]建立了考虑胶结作用的木质素固化粉土的边界面模型。邓肯-张模型参数少、物理意义明确,且能够反映土体应力-应变关系的非线性,因此,胡亚元等[10]提出了考虑纤维掺入量的水泥土邓肯-张模型;孙凯等[11]基于水泥土的结构性,建立了符合水泥土力学特性的弹塑性本构模型;然而,在传统硅酸盐水泥型固化剂的生产过程中会产生大量的废气和灰尘,对环境造成严重的污染[12]。于是,朱剑锋等[13]研制了节能环保型镁质水泥复合固化剂(TZ18)来替代传统硅酸盐水泥并取得了良好的固化效果;在此基础上,饶春义等[14]提出了镁质水泥固化土的一维压缩模型。但是,上述固化土本构模型大多仅考虑了单一因素(如水泥掺量等)对固化土力学性质的影响,而无法预测多重因素影响下(如初始含水量、龄期、固化剂掺量等)固化土的力学特性。鉴于初始含水量(w)、固化剂掺量(Wg)和龄期(T)对水泥固化土的力学性能的显著影响[1-6,15-16],本文作者基于岩土工程中广泛应用的邓肯-张模型[10,17-18],通过开展不同初始含水量、固化剂掺量和龄期下硫氧镁水泥固化土不排水三轴试验,研究各因素对邓肯-张模型参数的影响规律,并综合考虑这3种因素的影响建立硫氧镁水泥固化土修正邓肯-张模型。
1 试验材料与方案
1.1 试验材料
选用宁波②2-2层淤泥质黏土为试验用土,其物理力学指标见表1,其中,w为土样的天然含水量,γ为重度,e为孔隙比,wp为塑限,wL为液限,Es1-2为压缩模量,c为黏聚力,φ为内摩擦角。将淤泥质土烘干、碾碎、过孔径2 mm筛。试验采用镁质水泥复合固化剂TZ18[13]。
表1 土样的物理力学指标
Table 1 Physical and mechanical properties of soil

1.2 试验方案
考虑初始含水量w、固化剂掺量Wg和龄期T对硫氧镁水泥固化土力学性能的影响,设置试验方案,如表2所示,M0为基准配比试样,每种配比试样制备3个平行试样。
表2 硫氧镁水泥固化土三轴试验方案
Table 2 Triaxial test plan for soft soil solidified by magnesium oxysulfate cement

首先,将淤泥质黏土烘干,然后按照设计配比称取过筛后的干土、水、改性硫氧镁水泥和外加剂(水玻璃、熟料、硅灰)充分搅拌成均匀的复合固化剂(TZ18)混合浆液,将其缓缓注入到试验淤泥中,并充分混合搅拌均匀。最后分3层装入三瓣膜(直径×高度为39.1 mm×80.0 mm)中,每层振捣2~3 min排出气泡。试样在自然条件下养护2 d后拆模,然后移至恒温通风环境下继续养护至设计龄期。由于水化反应作用,硫氧镁水泥固化土试样养护过程会有一定的收缩,因此,在三轴试验前需要将试样上下平面打磨光滑,并测量其直径和高度,后续计算以实测体积为依据。
1.3 试验仪器与方法
镁质水泥固化土的不排水三轴试验在GDS高压与非饱和土动三轴仪器上进行,将试样装在加载底座上,然后加上压力室,采用GDSLAB软件设置试验参数和数据收集,其中,轴力传感器与顶帽的接触轴力为5.6 N,试验的围压σ3分别为100,200,300 kPa,围压的加载速率为0.02 kPa/s,剪切速率为0.05%/min,当轴向应变达到20%或轴力达到2 MPa 时试验自动停止[19]。
2 试验结果
2.1 硫氧镁水泥固化土的破坏形态
硫氧镁水泥固化土侧向鼓胀破坏形态如图1所示。可见,硫氧镁水泥固化土的破坏形式主要有:1) 侧向鼓胀破坏,试验后固化土表面没有明显的裂纹,大约在中间部位对称鼓起。这是由于TZ18固化剂水化反应生成的针状晶体[20]和胶体(由TZ18固化剂中的外加剂熟料、硅灰等反应生成)较少,且没有硬化胶结在一起形成一个结构体,固化土的强度低,具有较大的塑性,在较大的应变下发生破坏;2) 斜向剪切破坏,试验后固化土表面有明显的破裂面,破裂面与水平方向大致成45°~60°(见图2)。这是因为水化反应生成的晶体和胶体把分散的土颗粒黏结在一起,贯穿整个试样的内部,形成一定的结构,从而能抵抗较大的荷载作用。

图1 硫氧镁水泥固化土侧向鼓胀破坏形态
Fig. 1 Lateral bulging failure morphology of soft soil solidified by magnesium oxysulfate cement

图2 硫氧镁水泥固化土斜向剪切破坏形态
Fig. 2 Oblique shear failure morphology of soft soil solidified by magnesium oxysulfate cement
2.2 硫氧镁水泥固化土的应力-应变曲线
2.2.1 基准配比下的固化土三轴试验结果

图3 基准试样M0的应力-应变曲线
Fig. 3 Stress-strain curves of solidified soils sample M0
图3所示为基准试样M0的应力-应变曲线,其中,σ1-σ3为主应力差;ε1为轴向应变。由图3可知:在基准配比下,硫氧镁水泥固化土应力-应变曲线呈双曲线形式,且与淤泥质土三轴试验结果类似[19]:围压越大,曲线的初始切线斜率越大并且渐进线越高。

图4 不同初始含水量下的硫氧镁水泥固化土的应力-应变曲线
Fig. 4 Stress-strain curves of soft soils solidified by magnesium oxysulfate cement with different initial water contents
2.2.2 不同初始含水量的固化土三轴试验结果
图4所示为不同初始含水量淤泥固化后的应力-应变曲线关系,其中,Wg=15%,T=7 d。由图4可知:当初始含水量为40%~45%,围压一定时,随着固化土轴向应变ε1的增大,主应力差(σ1-σ3)先增大到峰值,然后下降,直到保持在稳定值附近,固化土的应力-应变曲线属于加工软化型;随着含水量的增加,硫氧镁水泥固化土的强度和刚度(初始切线模量)逐渐降低,应力-应变曲线逐渐由加工软化型转化为加工硬化型。这是因为w的增加提高了软土的孔隙比,降低了水化反应的离子浓度,抑止了硫氧镁水泥的水化反应,从而降低了硫氧镁水泥固化土的强度和刚度。另外,当w一定时,随着围压的增加,固化土逐渐被压密,从而提高了其刚度及强度。
2.2.3 不同固化剂掺量下的固化土三轴试验结果

图5 不同固化剂掺量下的硫氧镁水泥固化土的应力-应变曲线
Fig. 5 Stress-strain curve of soft soils solidified by magnesium oxysulfate cement with different curing agents contents
图5所示为不同固化剂掺量的固化土在不同围压下的应力-应变曲线关系,其中,w=50%, T=7 d。可见:Wg介于5%~15%且围压一定时,固化土的主应力差(σ1-σ3)随着轴向应变ε1的增大而增大,应力-应变关系呈加工硬化型。随着Wg的增加,硫氧镁水泥固化土的强度和刚度逐渐提高,应力-应变曲线逐渐由加工硬化型转化为加工软化型。这主要是因为Wg增加提高了水化反应的离子浓度,生成了更多的固化产物,减小了淤泥中的孔隙比,并形成一定空间网格结构,使得硫氧镁水泥固化土的强度和刚度较原状淤泥质土均得到了显著提高。
2.2.4 不同龄期下的硫氧镁水泥固化土三轴试验结果
图6所示为不同龄期的固化土在不同围压下的应力-应变关系,其中,w=50%,Wg=15%。从图6可以看出:龄期较短时,固化土的主应力差(σ1-σ3)较小,随着龄期的增长固化土的主应力差有较大的变化。龄期在3~7 d时,固化土的应力-应变曲线属于加工硬化型,随着龄期的增长,固化土固化产物逐渐增多,对原状淤泥质土的微观结构产生了较好胶结和填充,从而使得固化土的强度和刚度逐渐增大,应力-应变曲线逐渐转化为加工软化型。

图6 不同龄期下硫氧镁水泥固化土的应力-应变曲线
Fig. 6 Stress-strain curves of soft soils solidified by magnesium oxysulfate cement under different ages
3 硫氧镁水泥固化土修正邓肯-张本构模型
3.1 邓肯-张模型简介
由图3~6可知:随着含水量、固化剂掺量和龄期的变化,硫氧镁水泥固化土的应力-应变曲线主要表现为加工硬化型和软化型,对于硬化型曲线及软化型曲线的峰前阶段,可采用邓肯-张模型来进行模拟:
 (1)
(1)
式中:a和b为试验常数,且a=1/Ei,b=1/(σ1-σ3)ult,(σ1-σ3)ult为双曲线渐近线对应的极限偏差应力,Ei为应力-应变曲线的初始切线模量,与围压存在以下的函数关系:
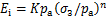 (2)
(2)
式中:K和n为模型参数;pa为标准大气压,本文取pa=101.3 kPa。定义破坏比Rf为[17]
 (3)
(3)
其中:(σ1-σ3)f为破坏应力,根据摩尔-库仑强度准则,有:
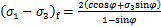 (4)
(4)
综上,原始邓肯-张模型共有K,n,c,φ,Rf 5个参数,可通过三轴试验进行标定。
3.2 硫氧镁水泥固化土的变形参数及破坏比
硫氧镁水泥固化土的Ei可近似用下式计算[17]:

 (5)
(5)
其中,下标95%和下标70%分别代表当(σ1-σ3)为(σ1-σ3)f的90%和70%时的试验数据;对于图3~6所示的加工硬化型应力-应变曲线,取ε1=15%时的主应力差为(σ1-σ3)f[19],对加工软化型,则取峰值处的主应力差为(σ1-σ3)f;(σ1-σ3)ult可近似通过下式计算:
 (6)
(6)
根据式(5)和(6)可得试样M0~M12的初始切线模量Ei(见图7)。对式(2)两边均除以pa,并取对数可得:
 (7)
(7)

图7 不同围压下硫氧镁水泥固化土的初始切线模量Ei
Fig. 7 Ei of soft soils solidified by magnesium oxysulfate cement under different confining pressures
将初始切线模量Ei和σ3代入式(7)可得试样M0~M12的参数K和n,见图8(a)和(b)。从图8(a)和(b)可以看出:模型参数n在0.803~0.828之间变化,可近似认为n不受含水量、固化剂掺量以及龄期的影响,取其平均值(n=0.812)作为硫氧镁水泥固化土本构模型参数n的经验值。
根据式(3)和(6)并结合试验结果可得各试样的破坏比Rf,如图8(c)所示。由图8(c)可知:硫氧镁水泥固化土的Rf波动范围较小,取其平均值(Rf=0.822)作为硫氧镁水泥固化土修正邓肯-张模型参数Rf经验值。

图8 硫氧镁水泥固化土的模型参数
Fig. 8 Model parameters of soft soils solidified by magnesium oxysulfate cement
3.3 硫氧镁水泥固化土的抗剪强度参数
试样M0~M12的黏聚力c和内摩擦角φ见图9。由图8和图9可知:原始邓肯-张模型参数n和Rf受w,Wg和T影响较小,可近似取n=0.812和Rf=0.822作为硫氧镁水泥固化土的模型参数经验值。而K,c和φ对它们比较敏感。因此,有必要对原始邓肯-张模型进行修正,使其关键参数K,c和φ能体现w,Wg和T的影响,从而实现不同条件下的硫氧镁水泥固化土的力学特性精确预测。

图9 硫氧镁水泥固化土的强度参数
Fig. 9 Shear strength parameters of soft soils solidified by magnesium oxysulfate cement
3.4 硫氧镁水泥固化土的修正邓肯-张模型
硫氧镁水泥固化土中的水来源于淤泥的初始含水量和固化剂中的水,可以通过灰水比(C/W)来综合考虑初始含水量(w)和固化剂掺量(Wg)的固化土模型参数间的关系[21-23]:
 (8)
(8)
式中:ws/Cs为固化剂的水灰比,且ws/Cs=0.155[13]。通过计算得出基准试验方案的硫氧镁水泥固化土的灰水比C0/W0=0.421,其中,C0和W0分别为基准配比下固化剂中固态材料和水的质量分数,C0为12.68%,W0为52.33%。
3.4.1 参数K的经验公式
根据图8(a)和式(8)可得归一化处理后参数K与灰水比的关系曲线,如图10(a)所示。由图10(a)可知:当灰水比较小时,K变化不大,随着灰水比增大,K缓慢增大;当灰水比较大时,K增长非常快,经拟合K与灰水比之间近似呈下述函数关系:
 (9)
(9)
式中:K0为基准配比的镁质中水泥固化土的原始邓肯-张模型参数K;d1和f1为综合考虑灰水比对参数K影响的参数,本文取d1=1.018,f1=4.360。
由图8可知:固化土的参数K不仅与灰水比有关,与养护龄期也有很大的关系。以基准配比的硫氧镁水泥固化土的模型参数K0和灰水比(C/W)0为基础,对归一化后的K与龄期进行拟合,结果见图10(b)。由图10(b)可知:随着龄期增长,K呈幂函数增长,通过拟合得到参数K与T的经验关系为
 (10)
(10)
式中: 为龄期归一化参考值,本文取
为龄期归一化参考值,本文取 =7 d;d2和f2为龄期对K的影响参数,本文取d2=0.723,f2=4.071。
=7 d;d2和f2为龄期对K的影响参数,本文取d2=0.723,f2=4.071。
假设龄期与硫氧镁水泥固化土参数K存在如式(10)所示的对数关系,即可建立综合考虑w,Wg和T影响的硫氧镁水泥固化土参数K的经验公式:
 (11)
(11)

图10 K与灰水比和龄期的关系
Fig. 10 Relationship between K and cement-water ratio and age

图11 抗剪强度指标与灰水比的关系
Fig. 11 Relationship between shear strength parameters and cement-water ratio
3.4.2 抗剪强度指标c和φ的经验公式
根据图9和式(8)可分别得到归一化处理后的参数c和φ与水灰比之间的关系曲线,见图11。由图11可知:与K-C/W关系类似,随着灰水比增加,固化土的c呈幂函数形式增大,φ呈线性增大。对图11所示结果进行拟合,可以分别得到c和φ与灰水比之间的经验公式:
 (12)
(12)
 (13)
(13)
式中:c0和φ0分别为基准配比的硫氧镁水泥固化土试样的黏聚力和内摩擦角;d3和f3为综合考虑灰水比对参数c影响的参数;d5为综合考虑灰水比对参数φ影响的参数。本文取d3=1.024,f3=2.827,d5=1.082。

图12 抗剪强度指标与龄期的关系
Fig. 12 Relationship between shear strength parameters and age
以基准配比的硫氧镁水泥固化土试样的黏聚力c0、内摩擦角φ0以及灰水比(C/W)0为基础,分别对归一化后的c和φ与龄期进行拟合,结果见图12。与图11类似,随着龄期增加,固化土的c和φ分别呈幂函数和线性形式增大,对图12拟合,可得:
 (14)
(14)
 (15)
(15)
式中:d4和f4为龄期对c的影响参数;d6为龄期对φ的影响参数。本文取d4=0.937,f4=1.712,d6=0.961。
分别以式(12)和式(13)中的c和φ替换式(14)和式(15)中的c0和φ0,可建立综合考虑初始含水量、固化剂掺量和龄期影响的硫氧镁水泥固化土抗剪强度指标c和φ的经验公式:
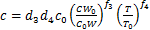 (16)
(16)
 (17)
(17)
3.4.3 修正邓肯-张模型
硫氧镁水泥固化土的力学性质受初始含水量w、固化剂掺量Wg和龄期T影响较大,其本构模型必须考虑上述因素影响才能准确描述固化土力学特性。根据以上试验结果,结合式(1),(2),(4),(11),(16)和(17)可建立如式(18)所示综合考虑w,Wg和T影响的硫氧镁水泥固化土修正邓肯-张模型。该模型包含5个模型参数c0,φ0,K0,Rf,n,3个基准参数c0,W0,T0以及10个拟合参数d1,d2,d3,d4,d5,d6,f1,f2,f3,f4,且所有参数通过三轴试验即可确定。
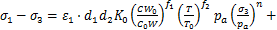



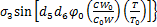 (18)
(18)
4 模型验证
为验证本文硫氧镁水泥固化土修正邓肯-张模型的合理性,选取宁波②2-2层淤泥质黏土制样,控制淤泥的初始含水量分别为40%,42%和50%,固化剂掺量分别为7%,10%和20%,养护龄期分别为5,7和9 d,进行常规三轴不排水剪切试验,C0=12.68%,W0=52.33%,T0=7 d,其他模型参数见表3,实测数据和模型预算结果见图13。由图13(c),(d),(e),(g)可知:对于加工硬化型曲线,本文修正邓肯-张模型的预测结果始终与试验结果一致。而对于加工软化型曲线,仅对峰值前的试验结果进行预测,结果见图13(a),(b),(f),(h)。由图13(a),(b),(f),(h)可知:修正邓肯-张模型可较好地预测峰值前的加工软化型应力-应变曲线。因此,本文硫氧镁水泥固化土修正邓肯-张模型较好地实现了任意初始含水量、固化剂掺量和龄期下固化土应力-应变关系的准确预测。
表3 硫氧镁水泥固化土模型参数
Table 3 Model parameters of soft soils solidified by magnesium oxysulfate cement


图13 硫氧镁水泥固化土的应力-应变实测值与预测值
Fig. 13 Measured and predicted stress-strain curves of soft soil solidified by magnesium oxysulfate cement
5 结论
1) 初始含水量、固化剂掺量和龄期对固化剂水化反应速度、水化产物的数量和凝胶材料硬化程度均产生不同程度影响,从而使得硫氧镁水泥固化土的强度和结构性有较大区别。硫氧镁水泥固化土的破坏形式主要分为侧向鼓胀破坏和斜向剪切破坏,硫氧镁水泥固化土的应力-应变关系分别呈加工硬化和软化2种类型。
2) 初始含水量、固化剂掺量和龄期对邓肯-张模型参数c,φ,K影响显著,而对n和Rf基本没有影响。
3) 通过引入灰水比的概念,并考虑龄期的影响,建立了硫氧镁水泥固化土的参数c,φ,K与w,Wg和T的经验公式,并提出了考虑3种因素影响的硫氧镁水泥固化土的修正邓肯-张模型。算例验证表明,该模型能准确预测加工硬化型和峰值前的加工软化型硫氧镁水泥固化土的应力-应变曲线。
4) 本文提出的修正邓肯-张模型无法预测硫氧镁水泥固化土的软化特性、剪胀性和塑性变形,在下一步研究中,将采用弹塑性或亚塑性模型来描述硫氧镁水泥固化土的力学特性。
参考文献:
[1] 朱伟, 张春雷, 高玉峰, 等. 海洋疏浚泥固化处理土基本力学性质研究[J]. 浙江大学学报(工学版), 2005, 39(10): 1561-1565.
ZHU Wei, ZHANG Chunlei, GAO Yufeng, et al. Fundamental mechanical properties of solidified dredged marine sediment[J]. Journal of Zhejiang University(Engineering Science), 2005, 39(10): 1561-1565.
[2] 董邑宁, 张青娥, 徐日庆, 等. 固化剂对软土强度影响的试验研究[J]. 岩土力学, 2008, 29(2): 475-478.
DONG Yining, ZHANG Qinge, XU Riqing, et al. The experimental research of strength with solidifying agent on clay[J]. Rock and Soil Mechanics, 2008, 29(2): 475-478.
[3] KOLIAS S, KASSELOURI-RIGOPOULOU V, KARAHALIOS A. Stabilisation of clayey soils with high calcium fly ash and cement[J]. Cement and Concrete Composites, 2005, 27(2): 301-313.
[4] HORPIBULSUK S, RACHAN R, CHINKULKIJNIWAT A, et al. Analysis of strength development in cement-stabilized silty clay from microstructural considerations[J]. Construction and Building Materials, 2010, 24(10): 2011-2021.
[5] 徐日庆, 畅帅, 俞元洪, 等. 基于响应面法的杭州海相软土固化强度模型[J]. 浙江大学学报(工学版), 2014, 48(11): 1941-1946.
XU Riqing, CHANG Shuai, YU Yuanhong, et al. Model of strength developed with response surface methodology for solidified marine soft clay of Hangzhou[J]. Journal of Zhejiang University(Engineering Science), 2014, 48(11): 1941-1946.
[6] 杨爱武, 钟晓凯, 梁超, 等. 吹填泥浆固化及长期力学性能试验研究[J]. 岩土力学, 2017, 38(9): 2589-2596.
YANG Aiwu, ZHONG Xiaokai, LIANG Chao, et al. Experiment study of solidification performance and long-term mechanical properties of dredger filled mud[J]. Rock and Soil Mechanics, 2017, 38(9): 2589-2596.
[7] 童小东, 龚晓南, 蒋永生. 水泥加固土的弹塑性损伤模型[J]. 工程力学, 2002, 19(6): 33-38.
TONG Xiaodong, GONG Xiaonan, JIANG Yongsheng. Elastic-plastic damage model of cement-stabilized soil[J]. Engineering Mechanics, 2002, 19(6): 33-38.
[8] 王军, 丁光亚, 潘林有, 等. 静三轴试验中水泥土力学特性及本构模型研究[J]. 岩土力学, 2010, 31(5): 1407-1412.
WANG Jun, DING Guangya, PAN Linyou, et al. Study of mechanics behavior and constitutive model of cemented soil under static triaxial tests[J]. Rock and Soil Mechanics, 2010, 31(5): 1407-1412.
[9] 张涛, 刘松玉, 蔡国军. 考虑胶结作用的木质素固化粉土边界面塑性模型[J]. 岩土工程学报, 2016, 38(4): 670-680.
ZHANG Tao, LIU Songyu, CAI Guojun. Boundary surface plasticity model for lignin-treated silt considering cementation[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(4): 670-680.
[10] 胡亚元, 余启致, 张超杰, 等. 纤维加筋淤泥固化土的邓肯-张模型[J]. 浙江大学学报(工学版), 2017, 51(8): 1500-1508.
HU Yayuan, YU Qizhi, ZHANG Chaojie, et al. Duncan-Chang model for fiber reinforced solidified sludge[J]. Journal of Zhejiang University(Engineering Science), 2017, 51(8): 1500-1508.
[11] 孙凯, 陈正林, 路德春. 一种考虑黏聚强度的改良土弹塑性本构模型[J]. 岩土力学, 2018, 39(5): 1589-1597.
SUN Kai, CHEN Zhenglin, LU Dechun. An elastoplastic constitutive model incorporating cementation effect of stabilizer-treated soils[J]. Rock and Soil Mechanics, 2018, 39(5): 1589-1597.
[12] 李勇, 赵应权, 邹长明. 水泥粉尘对农田土壤污染的环境磁学响应[J]. 环境科学学报, 2018, 38(5): 2023-2033.
LI Yong, ZHAO Yingquan, ZOU Changming. Magnetic response of cement dust to farmland soil pollution[J]. Acta Scientiae Circumstantiae, 2018, 38(5): 2023-2033.
[13] 朱剑锋, 饶春义, 庹秋水, 等. 硫氧镁水泥复合固化剂加固淤泥质土的试验研究[J]. 岩石力学与工程学报, 2019, 38(S1): 3206-3214.
ZHU Jianfeng, RAO Chunyi, TUO Qiushui, et al. Experimental study on the properties of the organic soil solidified by the composite magnesium oxysulfate cement-curing agent[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(S1): 3206-3214.
[14] 饶春义, 朱剑锋, 潘斌杰, 等. 基于扰动状态概念理论的固化淤泥一维压缩模型[J]. 岩土工程学报, 2019, 41(S1): 173-176.
RAO Chunyi, ZHU Jianfeng, PAN Binjie, et al. One-dimensional compression model for solidified silt based on theory of disturbed state concept[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(S1): 173-176.
[15] 畅帅, 徐日庆, 李雪刚, 等. 2种复合固化剂作用下有机质土的渗透性[J]. 中南大学学报(自然科学版), 2014, 45(6): 2021-2028.
CHANG Shuai, XU Riqing, LI Xuegang, et al. Permeability of organic soil treated with two composite stabilizers[J]. Journal of Central South University(Science and Technology), 2014, 45(6): 2021-2028.
[16] 王东星, 徐卫亚. 固化淤泥长期强度和变形特性试验研究[J]. 中南大学学报(自然科学版), 2013, 44(1): 332-339.
WANG Dongxing, XU Weiya. Experimental study on long-term strength and deformation properties of solidified sediments[J]. Journal of Central South University(Science and Technology), 2013, 44(1): 332-339.
[17] 徐日庆, 张俊, 朱剑锋, 等. 考虑扰动影响的修正Duncan-Chang模型[J]. 浙江大学学报(工学版), 2012, 46(1): 1-7.
XU Riqing, ZHANG Jun, ZHU Jianfeng, et al. Modified Duncan-Chang model considering disturbance[J]. Journal of Zhejiang University(Engineering Science), 2012, 46(1): 1-7.
[18] 邓湘君. 基于Duncan-Chang模型的地基沉降分层总和分析方法探讨[D]. 长沙: 湖南大学土木工程学院, 2013.
DENG Xiangjun. Layerwise summation method for ground foundation settlement based on Duncan-Chang constitutive model[D]. Changsha: Hunan University. College of Civil Engineering, 2013.
[19] SL237—1999. 土工试验规程[S].
SL237—1999. Specification of Soil Test[S].
[20] 巴明芳, 朱杰兆, 薛涛, 等. 原料摩尔比对硫氧镁胶凝材料性能的影响[J]. 建筑材料学报, 2018, 21(1): 124-130.
BA Mingfang, ZHU Jiezhao, XUE Tao, et al. Influence of molar ratio on properties of magnesium oxysulfate cementitious materials[J]. Journal of Building Materials, 2018, 21(1): 124-130.
[21] 朱剑锋, 庹秋水, 邓温妮, 等. 镁质水泥复合固化剂固化有机质土的抗压强度模型[J]. 浙江大学学报(工学版), 2019, 53(11): 2168-2174.
ZHU Jianfeng, TUO Qiushui , DENG Wenni, et al. Model of compressive strength of cured organic soil solidified by magnesium cement complex curing agent[J]. Journal of Zhejiang University(Engineering Science), 2019, 53(11): 2168-2174.
[22] HORPIBULSUK S, MIURA N, NAGARAJ T S. Assessment of strength development in cement-admixed high water content clays with Abrams' law as a basis[J]. Géotechnique, 2003, 53(4): 439-444.
[23] LORENZO G A, BERGADO D T. Fundamental parameters of cement-admixed clay: new approach[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2004, 130(10): 1042-1050.
(编辑 赵俊)
收稿日期: 2019 -09 -11; 修回日期: 2019 -11 -23
基金项目(Foundation item):国家自然科学基金资助项目(51879133, 51409142, 41672264);浙江省自然科学基金资助项目(LY17E080006) (Projects(51879133, 51409142, 41672264) supported by the National Natural Science Foundation of China; Project(LY17E080006) supported by the Zhejiang Provincial Natural Science Foundation)
通信作者:徐日庆,博士,教授,从事软土加固机理及本构关系研究;E-mail: xurq@zju.edu.cn