DOI: 10.11817/j.ysxb.1004.0609.2020-39168
TiAl合金的物理本构模型与加工图
任书杰1, 2,王克鲁1,鲁世强1,刘大博2,田 野2,罗 飞2
(1. 南昌航空大学 航空制造工程学院,南昌 330063;
2. 北京航空材料研究院,北京 100095)
摘 要:借助热模拟试验机研究TiAl合金在变形温度为1273~1523 K、应变速率为 0.001~1 s-1和变形程度为50%条件下的热变形行为;分析流变应力曲线特征,构建基于应变补偿的物理本构模型;考虑TiAl合金的弹性模量和自扩散系数与温度的关系,基于动态材料模型建立该合金的加工图,确立合适的热加工工艺参数。结果表明:TiAl合金具有正应变速率敏感性和负温度敏感性,流变应力曲线主要表现为动态再结晶软化机制;所建立的物理本构模型的预测值与实验值具有较好的吻合度;根据加工图的分析,该合金适宜的变形参数范围为1360~1523 K、0.001~0.02 s-1。
关键词:TiAl合金;物理本构模型;加工图;流变应力
文章编号:1004-0609(2020)-06-1289-08 中图分类号:TG146.2 文献标志码:A
TiAl基合金以其轻质、高强等特点成为替代部分镍基合金的高温结构材料之一,主要应用于航空、航天动力系统结构件,可实现推重比和燃油效率的大幅度提高[1-2]。近年来,应用本构模型探索TiAl基合金的热变形行为已有一些报道[3-4],但所构建的本构模型大多是基于Arrhenius型唯象本构方程,无法有效揭示材料的物理特性,而基于物理的本构模型将宏观变量与物理变量进行有效融合,在预测材料流变应力的同时还可以反映出材料的物理特性。然而,复杂的物理本构模型中涉及的公式较多,材料参数识别难,且运算量大,不利于构建[5]。对此,CABRERA等[6]基于蠕变理论提出了一种简便的物理本构模型,其考虑了温度对材料弹性模量和自扩散系数的影响,并借助双曲正弦函数实现了材料热变形行为的预测,其中建立该模型的关键之处在于准确获取材料的弹性模量和自扩散系数与温度之间的关系,而获得这种关系较为困难,因此其发展有些受限。魏海莲等[7]利用γ-Fe的物理参数建立C-Mn钢的物理本构方程,并取得较好的预测效果。MIRZADEH[8-10]应用该模型已成功预测了不锈钢、镁合金和铝合金的热变形行为。但上述的材料物理参数均源自于FROST等[11]提供的数据,是否符合实验材料固有的物理参数有待考证。KROLL等[12]和SCHAFRIK[13]对TiAl合金的自扩散系数和弹性模量有所研究,并建立了各自随温度的函数关系,因此,可用于构建该合金基于物理的本构方程。
目前,基于动态材料模型(Dynamic material model,DMM)[14]的加工图技术已在钛合金、镁合金、铝合金以及合金钢等材料中得到应用[15-19]。由于TiAl基合金属难变形材料,其热加工窗口较窄[20],而加工图的建立有助于制定和优化材料的热加工工艺参数,获得组织与性能优良的产品,避免材料在热变形时发生流变失稳现象。本文作者主要研究了TiAl合金在不同变形温度和应变速率下的压缩行为,建立了表征材料热变形行为的物理本构模型,并利用Prasad失稳判据的加工图对材料塑性安全区和失稳区进行了相关分析,确立了TiAl合金的热加工工艺参数。
1 实验
用于热压缩实验的原材料为TiAl合金,属γ基钛合金,其主要化学成分如表1所示。
表1 TiAl合金的化学成分
Table 1 Chemical compositions of TiAl alloy (mass fraction, %)

热压缩实验设备选用Gleeble-3500型热模拟试验机,实验前需将原材料冷加工成直径8 mm×12 mm的小圆柱体试样,并在其两端加工0.2 mm深的凹槽,主要用于存储高温润滑剂以减小压头与试样接触面的摩擦。实验热压缩工艺流程如图1所示,主要分为4个阶段,即加热、保温、压缩和冷却;压缩条件如下:变形温度为1273、1323、1373、1423、1473、1523 K,应变速率为0.001、0.01、0.1、1 s-1以及压缩量为50%。通过热模拟机配置的传感系统自动采集所需的数据,并利用Origin软件绘制压缩试样在热变形过程中的真应力-应变曲线。

图1 TiAl合金热压缩工艺流程图
Fig. 1 Hot compression process flow diagram for TiAl alloy
2 结果与分析
2.1 真应力-应变曲线
图2所示为TiAl合金在不同变形温度和应变速率下的真应力-应变曲线。由图2可以看出,变形温度和应变速率对流变应力的影响较为显著,且在较高的应变速率下具有非常明显的加工硬化现象,在较低的应变速率下呈现出一定的稳态流动特征。当变形温度和应变速率恒定时,随应变的增加,曲线具有典型的动态再结晶型曲线特征,即流变应力达到峰值以后出现显著的流变软化,这是由于该合金的层错能较低,易受热变形的影响发生动态再结晶。当温度或应变速率一定时,峰值应力随应变速率的增加而增大,随变形温度的升高而减小,表明该合金具有正应变速率敏感性和负温度敏感性。这是由于应变速率的增加会导致位错的大量增殖,同时减少动态再结晶的发生,进而提高了流变应力;相反,温度的升高会促进动态再结晶等热激活过程的发生,增强了动态软化,减少了加工硬化,使得流变应力下降。
2.2 基于物理的本构模型
2.2.1 本构模型的建立及修正
基于物理的热变形本构模型考虑了材料自扩散系数(D)和弹性模量(E)随温度的影响变化,不仅表征了合金的流变应力行为,还反映了材料的物理特性。由于峰值应力体现了材料在实验条件下最大的承载能力,因此,本文以峰值应力为例,构建该合金的物理本构方程,其表达式为
 (1)
(1)
 (2)
(2)
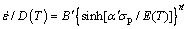 (3)
(3)
式中:D(T)和E(T)分别表示TiAl合金的自扩散系数和弹性模量与温度的关系[12-13]。其中,D0为扩散常数,1.53×10-4,Qsd为TiAl合金的Ti原子在γ相中的自扩散激活能;291000 J/mol; 、
、 、
、 均为待求参数,
均为待求参数, 值可参照式(3)的形式由指数方程和幂函数方程求解[8],即
值可参照式(3)的形式由指数方程和幂函数方程求解[8],即 。对应的指数方程和幂函数方程表示如下:
。对应的指数方程和幂函数方程表示如下:
 (4)
(4)
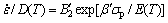 (5)
(5)
式中: 和
和 可通过
可通过 与
与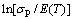 、
、 之间的曲线经线性拟合后得到的斜率确定,如图3(a)和(b)所示,求得
之间的曲线经线性拟合后得到的斜率确定,如图3(a)和(b)所示,求得 和
和 分别为5.613、2180.56,由此得到
分别为5.613、2180.56,由此得到 =388.48。
=388.48。

图2 不同变形条件下TiAl合金的真应力-应变曲线
Fig. 2 True stress-true strain curves of TiAl alloy under different deformation conditions
将式(3)两边取自然对数,整理得到:
 (6)
(6)
由式(6)可以看出,通过 与
与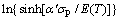 曲线经线性拟合得到的斜率和截距便可求出
曲线经线性拟合得到的斜率和截距便可求出 和
和 ,如图3(c)所示,拟合结果为
,如图3(c)所示,拟合结果为 =4.224和ln
=4.224和ln =28.49。基于所求的常数
=28.49。基于所求的常数 、ln
、ln 、
、 ,并结合式(1)和(2)整理后得到TiAl合金以峰值应力为数据的物理本构方程:
,并结合式(1)和(2)整理后得到TiAl合金以峰值应力为数据的物理本构方程:

 (7)
(7)
上述所求的物理本构模型只考虑了峰值应力,而未考虑应变对流变应力的影响,所建立的本构模型尚不能用来预测材料热变形的流变应力曲线。对此,本文引入应变因子,选取应变为0.05~0.69(间隔取0.04,共17个应变量)条件下对应的流变应力值,按照上述的材料常数求解方法,计算不同应变下对应的材料常数 、ln
、ln 和
和 ,并采用六次多项式线性回归拟合材料常数与应变之间的函数关系(见式(8)),以此构建应变补偿的物理本构模型:
,并采用六次多项式线性回归拟合材料常数与应变之间的函数关系(见式(8)),以此构建应变补偿的物理本构模型:
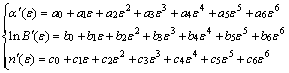 (8)
(8)
图4所示为材料常数 、ln
、ln 和
和 与应变之间的关系曲线。经六次多项式拟合得到的系数如表2所示。
与应变之间的关系曲线。经六次多项式拟合得到的系数如表2所示。
将系数代入式(8)并嵌入到式(3)中,可获得修正后的基于物理的本构模型:

 (9)
(9)

图3 不同变量之间的线性拟合关系
Fig. 3 Linear fitting relationships among different variables

图4 材料常数 、ln
、ln 和
和 与应变的六次多项式拟合关系
与应变的六次多项式拟合关系
Fig. 4 6th polynomial fitting relationships among material parameters  、ln
、ln ,
,  and true strain
and true strain
表2 材料常数 、ln
、ln 和
和 的六次多项式系数
的六次多项式系数
Table 2 6th polynomial coefficients of material parameters  , ln
, ln and
and 

2.2.2 本构模型的验证及误差分析

图5 本构模型预测值与实验值的比较及相关性分析
Fig. 5 Comparison of predicted and experimental values of constitutive modelat deformation temperature of 1423 K (a) and strain rate of 0.001 s-1 (b) and correlation analysis (c)
为验证不同变形温度、应变速率和应变下基于物理本构模型预测流变应力的准确性,对预测值和实验值进行了对比,所得结果如图5(a)和(b)所示。可以看出,由预测值与实验值绘制的真应力-应变曲线在实验范围内基本吻合。为了更加准确了描述所建立的物理本构模型的精确程度,本文通过平均相对误差(AARE)和相关系数Rr对本构方程预测的准确性进行进一步评定,相关表达式为
 (10)
(10)
 (11)
(11)
式中:E为实验值;P为预测值; 和
和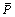 分别代表E和P的平均值;N为分析数据的个数。
分别代表E和P的平均值;N为分析数据的个数。
本文将预测的所有数据点与对应的实验值进行线性拟合,结果如图5(c)所示,得到该本构模型预测值与实验值之间的相关系数为0.981,平均相对误差为5.99%,表明所建立的物理本构模型具有较好的预测能力,可用于表征TiAl合金的热变形行为。
2.3 TiAl合金的加工图
2.3.1 加工图的原理及构建
根据动态材料模型(DMM)理论,工件在热变形时可看作一个能量耗散体,其在塑性变形时所耗散的能量G与组织转变所耗散的能量J之和等于外界输入工件的总能量P,可表示成:
 (12)
(12)
式中: 和
和 是两个互补函数,分别称为功率耗散量和功率耗散协量。在给定温度和应变下,材料对应变速率的动态响应(动态本构方程)为
是两个互补函数,分别称为功率耗散量和功率耗散协量。在给定温度和应变下,材料对应变速率的动态响应(动态本构方程)为
 (13)
(13)
式中:K是与温度有关的常数;m是应变速率敏感性指数,决定材料变形中的耗散量G与耗散协量J之间的比例关系,即 。由于J/Jmax的关系与材料的微观结构演化密切相关,被定义为功率耗散因子,用η表示,其中Jmax=P/2,当材料的流变应力满足式(14)的关系时,可推导出η表达式为
。由于J/Jmax的关系与材料的微观结构演化密切相关,被定义为功率耗散因子,用η表示,其中Jmax=P/2,当材料的流变应力满足式(14)的关系时,可推导出η表达式为
 (14)
(14)
式中:η为一个无量纲的参数,是表征材料在热变形时的能量耗散;对于理想的线性耗散过程,m,η=1;而对于非线性耗散过程,m,η<1;η随变形温度和应变速率变化的二维等值线图即为功率耗散图。
在DMM中,SIVAKESAVAM等[21]基于Ziegler大塑性流变理论的不可逆热力学极值原理建立了材料流变失稳判据:
 <0 (15)
<0 (15)
式中: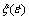 <0表明材料在所对应的变形温度和应变速率范围内进行塑性变形可能会发生诸如绝热剪切、局部塑性流动、楔形裂纹等失稳现象;
<0表明材料在所对应的变形温度和应变速率范围内进行塑性变形可能会发生诸如绝热剪切、局部塑性流动、楔形裂纹等失稳现象;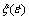 随变形温度和应变速率的变化可绘制流变失稳图。功率耗散图和流变失稳图叠加便可得到加工图。
随变形温度和应变速率的变化可绘制流变失稳图。功率耗散图和流变失稳图叠加便可得到加工图。
2.3.2 加工图的分析

图6 应变为0.1(a)和0.69(b)条件下TiAl合金的加工图
Fig. 6 Processing maps of TiAl alloy at strain ε=0.1(a) and ε=0.69(b)
根据TiAl合金真应力-应变曲线的流变应力,绘制出应变分别为0.1和0.69时的加工图,如图6所示。其中灰色区域为流变失稳区,其余为塑性安全区。一般来说,η值在0.3~0.6时,材料最有可能发生动态再结晶,当η>0.6时,可能出现超塑性[22];而失稳区的组织易出现绝热剪切、楔形裂纹等失稳现象,其η值较小。从图6(a)中可以看出,应变为0.1时,加工图中存在两个功率耗散因子η峰区,即1373 K 、0.001 s-1和1523 K、0.01 s-1附近,对应的η值均高于0.4。而失稳区主要分布在低温高应变速率和高温高应变速率区,表现出较低的功率耗散因子。当应变为0.69时,此时材料已承受较大的变形量,从图6(b)中可以看出,η峰区有三处,即1273~1378 K、0.001~0.01 s-1,1295~1340 K、0.47~1 s-1和1495~1523 K、0.001~0.01 s-1;且失稳区有所扩大,并延伸到低温低应变速率和中温高应变速率区。为了分析材料在变形过程中可能发生流变失稳的区域,绘制了应变在0.1、0.2、0.3、0.4、0.5、0.6和0.69条件下失稳区的叠加图(阴影部分),如图7所示。由图7可以看出,流变失稳区几乎占了加工图的一半区域,主要集中在高应变速率和低温低应变速率区,这也验证了该合金的热加工范围窄[20];结合功率耗散因子的变化,在η峰区1273~1378 K、0.001~0.01 s-1和1295~1340 K、0.47~1 s-1范围内也可能发生失稳现象,应注意避免在此区域热加工。综合上述分析,在1360~1523 K、0.001~0.02 s-1范围内的η值基本在0.3以上,表明TiAl合金在此区域内适合进行热加工。

图7 TiAl合金在不同应变下失稳叠加图
Fig. 7 Instability superimposed maps at different strain for TiAl alloy
3 结论
1) TiAl合金具有正应变速率敏感性和负温度敏感性;其流变应力曲线特征以动态再结晶软化机制为主。
2) 考虑温度对TiAl合金弹性模量和自扩散系数的影响,构建了基于应变补偿的物理本构方程,其预测值与实验值之间的相关系数为0.981,平均相对误差为5.99%,表明该本构模型可以用于预测TiAl合金在不同应变下的流变应力。
3) 应用动态材料模型理论,构建了基于Prasad失稳判据下的加工图及不同应变下的失稳叠加图,获得了该合金适合的热加工工艺参数范围为1360~1523 K、0.001~0.02 s-1。
REFERENCES
[1] 杨 锐. 钛铝金属间化合物的进展与挑战[J]. 金属学报, 2015, 51(2): 129-147.
YANG Rui. Advances and challenges of TiAl base alloys[J]. Acta Metallurgica Sinica, 2015, 51(2): 129-147.
[2] MA Teng-fei, CHEN Rui-run, ZHENG De-shuang, GUO Jing-jie, DING Hong-sheng, SU Yan-qing, FU Heng-zhi. Influence of high-temperature hydrogen charging on microstructure and hot deformability of binary TiAl alloys[J]. Journal of Alloys and Compounds, 2017, 701: 399-407.
[3] 王 刚, 徐 磊, 崔玉友, 杨 锐. 粉末冶金TiAl基合金高温变形行为及其本构模型[J]. 中国有色金属学报, 2010, 20(1): 269-273.
WANG Gang, XU Lei, CUI Yu-you, YANG Rui. High temperature deformation behavior of powder metallurgy TiAl alloy and its constitutive model[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(1): 269-273.
[4] CHEN Y Y, YANG F, KONG F T, XIAO S L. Constitution modeling and deformation behavior of yttrium bearing TiAl alloy[J]. Journal of Rare Earths, 2011, 29(2): 114-118.
[5] 曲 杰, 覃 威, 金泉林. 宏微观耦合本构模型参数识别取值范围研究[J]. 力学学报, 2014, 46(6): 920-930.
QU Jie, QIN Wei, JIN Quan-lin. Study on the parameter value domain of macro-micro constitutive model[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(6): 920-930.
[6] CABRERA J M, OMAR A A, PRADO J M, JONAS J J. Modeling the flow behavior of a medium carbon microalloyed steel under hot working conditions[J]. Metallurgical and Materials Transactions A, 1997, 28(11): 2233-2244.
[7] 魏海莲, 刘国权, 肖 翔, 张明赫. 表观的和基于物理的35Mn2钢奥氏体热变形本构分析[J]. 金属学报, 2013, 49(6): 731-738.
WEI Hai-lian, LIU Guo-quan, XIAO Xiang, ZHANG Ming-he. Apparent and physically based constitutive analyses for hot deformation of austenite in 35Mn2 steel[J]. Acta Metallurgica Sinica, 2013, 49(6): 731-738.
[8] MIRZADEH H. Constitutive modeling and prediction of hot deformation flow stress under dynamic recrystallization conditions[J]. Mechanics of Materials, 2015, 85(6): 66-79.
[9] MIRZADEH H. A comparative study on the hot flow stress of Mg-Al-Zn magnesium alloys using a simple physically-based approach[J]. Journal of Magnesium and Alloys, 2014, 2(9): 225-229.
[10] MIRZADEH H. Constitutive description of 7075 aluminum alloy during hot deformation by apparent and physically- based approaches[J]. Journal of Materials Engineering and Performance, 2015, 24(3): 1095-1099.
[11] FROST H J, ASHBY M F. Deformation-mechanism maps: The plasticity and creep of metals and ceramics[M]. Oxford: Pergamon Press, 1982.
[12] KROLL S, SOLWIJIK N A, HERZIG C, MEHRER H. Titanium self-diffusion in the intermetallic compound γ-TiAl[J]. Defect and Diffusion Forum, 1993, 95/98(6): 865-868.
[13] SCHAFRIK R E. Dynamic elastic moduli of the titanium aluminides[J]. Metallurgical and Materials Transactions A, 1977, 8(6): 1003-1006.
[14] PRASAD Y V R K, SESHACHARYULU T. Modeling of hot deformation for microstructural control[J]. International Materials Reviews, 1998, 43(6): 243-258.
[15] XU Xin, DONG Li-min, BA Hong-bo, ZHANG Zhi-qiang, YANG Rui. Hot deformation behavior and microstructural evolution of beta C titanium alloy in β phase field[J]. Transactions of Nonferrous Metals Society of China, 2016, 26(11): 2874-2882.
[16] CHEN Rui-run, MA Teng-fei, GUO Jing-jie, DING Hong-sheng, SU Yan-qing, FU Heng-zhi. Deformation behavior microstructural evolution of hydrogenated Ti44Al6Nb alloy during thermo-compression at 1373-1523 K[J]. Materials and Design, 2016, 108(10): 259-268.
[17] 肖宏超, 刘楚明, 徐 璐, 王 霄, 万迎春. Mg-10Gd-4.8Y-0.6Zr镁合金热变形行为与加工图[J]. 中国有色金属学报, 2013, 23(2): 303-310.
XIAO Hong-chao, LIU Chu-ming, XU Lu, WANG Xiao, WAN Ying-chun. Deformation behavior and processing map of Mg-10Gd-4.8Y-0.6Zr magnesium alloy[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(2): 303-310.
[18] LI Peng-wei, LI Hui-zhong, HUANG Lan, LIANG Xiao-peng, ZHU Ze-xiao. Characterization of hot deformation behavior of AA2014 forging aluminum alloy using processing map[J]. Transactions of Nonferrous Metals Society of China, 2017, 27(8): 1677-1688.
[19] BABU K A, MANDAL S, ATHREYA C N, SHAKTHIPRIYA B, SARMA V S. Hot deformation characteristics and processing map of a phosphorous modified super austenitic stainless steel[J]. Materials and Design, 2017, 115(2): 262-275.
[20] SRINIVASAN R, SINGH J P, TUVAL E, WEISS I. Isothemal deformation of gamma titanium aluminide[J]. Scripta Materialia, 1995, 34(8): 1295-1301.
[21] SIVAKESAVAM O, PRASAD Y V R K. Characteristics of superplasticity domain in the processing map for hot working of as-cast Mg-11.5Li-1.5Al alloy[J]. Materials Science and Engineering A, 2002, 323(1): 270-277.
[22] RAO K P, PRASAD Y, SURESH K. Hot working behavior and processing map of a γ-TiAl alloy synthesized by powder metallurgy[J]. Materials and design, 2011, 32(10): 4874-4881.
Physical constitutive model and processing map of TiAl alloy
REN Shu-jie1, 2, WANG Ke-lu1, LU Shi-qiang1, LIU Da-bo2, TIAN Ye2, LUO Fei2
(1. School of Aerospace Manufacturing Engineering, Nanchang Hangkong University, Nanchang 330063, China;
2. Beijing Institute of Aeronautical Materials, Beijing 100095, China)
Abstract: Hot deformation behavior of TiAl alloy was studied at the temperature range of 1273-1523 K, strain rate range of 0.001-1 s-1 and maximum deformation degree of 50% with thermal simulator. The characteristics of the flow stress curve were analyzed. The physical constitutive model based on strain compensation was constructed, which took into account the relationship between elastic modulus and self-diffusion coefficient and temperature for TiAl alloy. The suitable thermal processing parameter of the alloy were established by processing maps based on dynamic material model (DMM). The results show that TiAl alloy has positive strain rate sensitivity and negative temperature sensitivity, and the flow stress curves are mainly characterized by dynamic recrystallization softening mechanism. The predicted values of the physical constitutive model are in good agreement with the experimental values. According to the analysis of processing maps for the alloy, the range of appropriate thermal processing parameters are 1360-1523 K and 0.001-0.02 s-1.
Key words: TiAl alloy; physical constitutive model; processing map; flow stress
Foundation item: Project(YC2016033) supported by the Graduate Student Innovation Foundation of Nanchang Hangkong University, China; Project(51164030) supported by the National Natural Science Foundation of China; Project(GJJ160683) supported by the Education Commission Foundation of Jiangxi Province, China
Received date: 2018-10-09; Accepted date: 2019-02-26
Corresponding author: WANG Ke-lu; Tel: +86-13133804266; E-mail: wangkelu@126.com
(编辑 龙怀中)
基金项目:南昌航空大学研究生创新专项基金资助项目(YC2016033);国家自然科学基金资助项目(51464035);江西省教育厅科技项目(GJJ160683)
收稿日期:2018-10-09;修订日期:2019-02-26
通信作者:王克鲁,教授,博士;电话:13133804266;E-mail:wangkelu@163.com