J. Cent. South Univ. Technol. (2008) 15(s1): 009-012
DOI: 10.1007/s11771-008-303-5
Rheology elasticity determined by deformation of stretchable molecular trains
XIAO Jian-hua(肖建华)
(Measurement Institute, Henan Polytechnic University, Jiaozuo 454000, China)
Abstract: The average stretching direction, local rotation angular, and stretching ratio parameters of molecular trains were used to express the rheology deformation. Based on this micro geometrical deformation, the macro deformation of medium was expressed. Then, using intrinsic elasticity concept, the stress—strain relation was obtained. In this theoretic formulation, the response functions of extension ratio and rotation angular were used to express the rheology feature of medium. For medium composed by incompressible molecular trains, the local rotation angular divides rheology deformation into three kinds: viscoelastic deformation or elasticity enhancement, viscoplastic deformation or elasticity degenerate and constant elasticity range. These results explain the experimental features of rheology deformation well.
Key words: viscoplasticity; viscoelasticity; local rotation angular; extension ratio; deformation tensor; rational mechanics; rheology
1 Introduction
Rheology deformation has two basic types. One basic type is viscoelastic deformation. Under constant surface force action, the elasticity increases until it reaches a stress-dependent value. Initially, the deformation is fast, then gradually slows down, and finally stops. When the force is removed, the medium may return to its initial configuration, gradually.
Another basic type is viscoplastic deformation. Under constant stress action, the elasticity decreases until it reaches a stress-dependent value. Initially, the deformation is slow, then gradually speeds up, and finally becomes flow. When the stress is removed before the flow happens, the medium almost maintains the current configuration. For a practical medium, when force is big enough, the elastic deformation will become plastic deformation.
As viscoelastic and viscoplastic is usually related with the substructures of medium, the medium can be viewed as medium composed by molecular trains. Initially, the molecular trains are randomly distributed and orientated. This condition is equivalent with the isotropy of medium.
For a polymer molecular train, it can be stretched along an average direction. However, based on the molecular structure, this stretching is produced by the segment reorientation or its equivalent. Therefore, the traditional continuum deformation concept is not applicable directly. In molecular train sense, the “incompressibility” concept is applied to express this feature. Then, extending the classical strain to large deformation case, the neo-Hookeian elasticity is obtained.
For uniaxial extension ratio, ρ, the theoretic result[1]
is However, it is far away from experi-
However, it is far away from experi-
mental results for large extension ratio. It gives out liner relationship between rubber elasticity and stretching ratio. If Rivlin strain—energy function concept is used, similar results are obtained. However, for large extension, the theoretic predicted force is lower than experimental force[1].
Although statistical theory is applied to explain the neo-Hookeian elasticity with sound physical base, the final results is similar with Eqn.(1). Hence, no essential progress is made.
The essential problem is caused by mixing the micro geometry with the macro geometry of rubber. The former is extending the macro geometry to micro geometry by introducing “incompressibility” concept. The later is getting the macro geometry by statistical result of micro geometry directly. Both are partially correct.
In this research, the “incompressibility” concept was applied for the micro deformation of molecular trains. The statistical method was applied to get the average deformation parameters of micro geometry. Then, the macro deformation tensor[2-3] was obtained. By this way, the strain—stress relationship was established. Then, using intrinsic elasticity concept, the neo- Hookeian stress—strain relation was obtained.
2 Deformation tensor
For stretched molecular trains, on average sense, their deformation can be expressed by three extension ratios, i.e., ρ1, ρ2 and ρ3. For initially random orientation distribution, when extension stress is applied, each molecular train will rotate locally around the stress directions, i.e., L1, L2 and L3. Introducing average local rotation angular, θ, on average sense, the molecular train deformation tensor can be expressed as:
 (1)
(1)
where
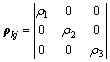 (2a)
(2a)
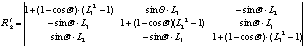 (2b)
(2b)
Defining the local intrinsic rotation angular parameter θ as:
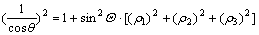 (3)
(3)
Then, the deformation tensor[4] can be rewritten as:
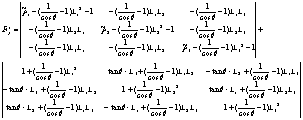 (4)
(4)
where
 (5a)
(5a)
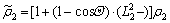 (5b)
(5b)
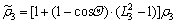 (5c)
(5c)
They are macro extension ratios.
3 Stress components
For macro uniaxial extension along direction L1 = 1 (L2 = L3 = 0), the volume average of deformation tensor is simplified as:
 (6)
(6)
The first tensor on the right side of Eqn.(6) is related with intrinsic stretching stress:
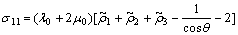 (7a)
(7a)
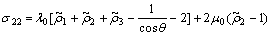 (7b)
(7b)
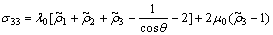 (7c)
(7c)
Here λ0 and μ0 are elastic constants of molecular trains. The second tensor on the right side of Eqn.(6) is an orthogonal rotation. It expresses the macro volume expansion of molecular trains.
On the other hand, using the incompressibility concept to molecular trains[1], the stretching ratio meets equation:
 (8)
(8)
For symmetry case, 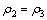 , letting
, letting 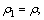 then
then 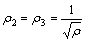 . Eqn.(3) becomes:
. Eqn.(3) becomes:
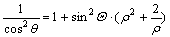 (9)
(9)
Eqn.(5) becomes:
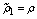 (10a)
(10a)
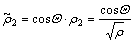 (10b)
(10b)
 (10c)
(10c)
Substituting Eqns.(9) and (10) into Eqn.(7a), the extension stress is
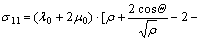
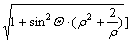 (11)
(11)
It is noted that, in Eqn.(10), the macro extension ratio is ρ.
4 Rubber elasticity
Physically, the micro average local rotation angular of molecular trains is determined by the material structures and dependents on temperature. It is limited by the allowable orientation variance[1, 5]. For many solid materials, it is very small. In fact, it can be measured by the deformation experiment. For a given maximum Θc (Θc<π/2, it can be viewed as a given material feature parameter), the yield stretching ratio λc is determined by the following equation.
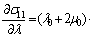
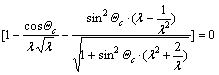 (12)
(12)
For 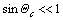 ,
, 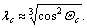 For
For 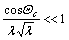 , the yield stretching ratio does not exist. In this case,
, the yield stretching ratio does not exist. In this case, 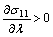 , the extension stress is rapidly increased along with the increase of stretching ratio. So, for large stretching ratio, the rubber elasticity is:
, the extension stress is rapidly increased along with the increase of stretching ratio. So, for large stretching ratio, the rubber elasticity is:
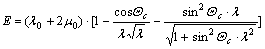 (13)
(13)
It is rapidly increased along with the increase of stretching ratio. It is much more rapidly than linear form. This is the intrinsic feature of practical rubber elasticity. It can be seen that it is well in accordance with experimental results.
For very large stretching ratio, it is approaching the final elasticity of rubber defined as:
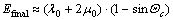 (14)
(14)
So, the final elasticity of rubber is determined by the molecular train elasticity and the maximum allowable local rotation angular of molecular train (or the micro structure). But it will be never bigger than the elasticity of molecular train. Hence, the infinite elasticity problem of Eqn.(1) is overcome.
For comparison, the rubber elasticity at small stretching ratio can be defined as (by λ≈1 and supposing the molecular train responds the extension tress very sensitively):
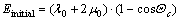 (15)
(15)
The rubber elasticity at small stretching ratio depends on the allowable orientation variance. The elasticity ratio of final elasticity over initial elasticity can be expressed by maximum local rotation angular Θc as:
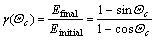 (16)
(16)
For small Θc, this value is very big. Hence, high rubber elasticity range can be achieved by high elasticity molecular train with little orientation allowance. When Θc = π/4, γ = 1. It means that, for good rubber materials, Θc<π/4 is a necessary condition. In fact, for Θc=30?, 15? and 5?, the elasticity ratios are 3.7, 54.0, and 240.0, respectively.
5 Rheology elastoplasticity
Physically, the micro average local rotation angular of molecular trains is limited by the allowable orientation variance[1, 5]. For many solid materials, it is very small. Based on viscoelasticity experiment, the macro extension ratio is an exponential function of time. When the extension ratio is changed from initial value ρini to end value ρend, if the characteristic response time is τ, the time-dependent macro extension ratio is:
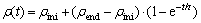 (17)
(17)
When 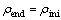 , it represents viscoelastic deformation. When
, it represents viscoelastic deformation. When  it represents viscoplastic deformation. In this case, the micro average local rotation angular Θ(t) is also time-dependent (for simplicity, it will be simply written as Θ).
it represents viscoplastic deformation. In this case, the micro average local rotation angular Θ(t) is also time-dependent (for simplicity, it will be simply written as Θ).
By Eqn.(11), the time-dependent extension stress is:
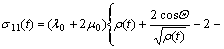
 (18)
(18)
Therefore, the time-dependent elasticity can be expressed as:
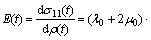
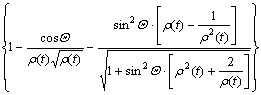 (19)
(19)
For very large time 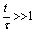 , the final elasticity is:
, the final elasticity is:
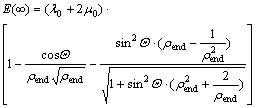 (20)
(20)
The initial elasticity (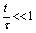 ) is:
) is:
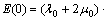
 (21)
(21)
For  the time-dependent elasticity is:
the time-dependent elasticity is:
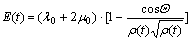 (22)
(22)
For 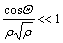 , the time-dependent elasticity is:
, the time-dependent elasticity is:
 (23)
(23)
It is clear that the local rotation angular is an important parameter of medium feature.
For initial isotropic medium if ρini=1, E(0)=(λ0+2μ0)? [1-cosΘ(0)]. For very large ρend, E(∞)=(λ0+2μ0)?[1- cosΘ(∞)]. Then the elasticity ratio of final elasticity over initial elasticity is:
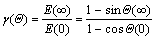 (24)
(24)
It can be divided into three ranges: (1) viscoelastic deformation or elasticity enhancement range, Θ<π/4, γ(Θ)>1; (2) viscoplastic deformation or elasticity degenerate range, Θ>π/4, γ(Θ)<1; (3) constant elasticity range, Θ≈π/4, γ(Θ)≈1. Therefore, the molecular average orientation variation range determines the intrinsic feature of medium. So, the local rotation parameter is the key factor for wide diversity of rheology deformation.
6 Constitutive equations
Based on above formulation, the constitutive equation in extension direction is:
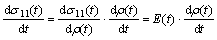 (25)
(25)
It is in stress rate and extension rate form. E(t) is defined by Eqn.(19).
Following the similar procedure, for the perpendicular direction, the 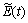 can be defined as:
can be defined as:
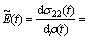

 (26)
(26)
The constitutive equation in perpendicular direction is:
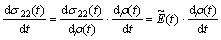 (27)
(27)
In many applications, the name strain 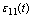 is used. It is defined as:
is used. It is defined as: 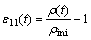 . In this case,
. In this case, 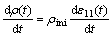 . So, the constitutive is equivalent with conventional form. In some applications, the true strain
. So, the constitutive is equivalent with conventional form. In some applications, the true strain 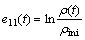 is used, In this case,
is used, In this case, 
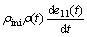 . Hence, the formulation of constitutive equation is applicable for both cases. When the extension ratio is expressed by the strain, the constitutive is nonlinear form.
. Hence, the formulation of constitutive equation is applicable for both cases. When the extension ratio is expressed by the strain, the constitutive is nonlinear form.
By Eqn.(17), the stress rate is:
the stress rate is:
 (28)
(28)
On average sense, omitting the variation of time- dependent elasticity, the stress is:
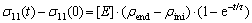 (29)
(29)
where 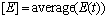 .
.
Hence, the linear viscoelasticity is only a rough approximation of rheology feature.
7 Conclusions
1) By improving the incompressibility concept and the statistical average method, the rheology elasticity is formulated, referring to the intrinsic molecular train elasticity.
2) For large stretching ratio, the rubber elasticity is rapidly increased along with the increase of stretching ratio. It is much more rapidly than linear form.
3) The average local rotation angular of molecular train is introduced to express the intrinsic feature of rheology deformation. It divides rheology deformation into three kinds, viscoelastic deformation or elasticity enhancement viscoplastic deformation or elasticity degenerate: and constant elasticity range. Then, the constitutive equations for extension direction and perpendicular direction are formulated.
References
[1] DAVID I. BOWER. An introduction to polymer physics [M]. Cambridge: Cambridge University Press, 2002.
[2] TRUESDELL C. The mechanical foundation of elasticity and fluid mechanics [M]. New York: Gordon and Breach Science Pub Inc, 1966.
[3] CHEN Zhi-da. Rational mechanics [M]. Xuzhou: China University of Mining and Technology Press, 1987. (In Chinese)
[4] XIAO Jian-hua, Decomposition of displacement gradient and strain definition [J]. Journal of Central South University of Technology, 2007, 14(s1): 401-404.
[5] DUNSTAN D E, HILL E K, WEI Y. Direct measurement of polymer segment orientation and distortion in shear: Semi-dilute solution behavior [J]. Polymer, 2004, 45: 1261-1266.
(Edited by YANG Hua)
Received date: 2008-06-25; Accepted date: 2008-08-05
Corresponding author: XIAO Jian-hua, PhD, Professor; Tel: +86-391-3987677; E-mail: jhxiao@hpu.edu.cn