J. Cent. South Univ. Technol. (2010) 17: 566-571
DOI: 10.1007/s11771-010-0524-2 
Tuning of fuzzy PID controller for Smith predictor
RONG Hui-gui(荣辉桂)1, 2, ZHENG Hui(郑蕙)3, LI Zheng-qiang(黎峥强)1, XIA Yu-xiang(夏宇翔)1
1. School of Software, Hunan University, Changsha 410082, China;
2. School of Information Management, Wuhan University, Wuhan 430072, China;
3. School of International Studies, Hunan University of Commerce, Changsha 410205, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2010
Abstract: An analytical tuning method was proposed for fuzzy PID controller used in Smith predictor in order to extend its application and improve its robustness. The fuzzy PID controller was expressed as a sliding mode control. Based on Lyapunov theory, Smith predictor was analyzed in time domain. The parameters of the fuzzy PID controller can be obtained using traditional linear control theory and sliding mode control theory. The simulation experiments were implemented. The simulation results show that the control performance, robustness and stability of the fuzzy PID controller are better than those of the PID controller in Smith predictor.
Key words: Smith predictor; Lyapunov theory; fuzzy PID controller; robustness
1 Introduction
There exists delay time in many industrial processes, such as chemical engineering, oil refining, metallurgy, and heat engineering processes [1-4]. For those processes, the Smith predictor is well known as an effective delay time compensator [5-6]. Thus, Smith predictor is widely applied to industrial process control based on proportional integral derivative (PID) controllers. It requires accurate mathematical model of controlled object. However, the accurate mathematical model cannot be obtained in practical industrial fields due to noise and disturbance.
In this complex environment, it is well-known that the fuzzy PID controller has better performance due to its inherent robustness [7-10]. Although the control performance of fuzzy PID controller in Smith predictor is better than that of conventional PID controller, it cannot interpret why fuzzy PID controller can give good performance [11-12]. One of key reasons is that the fundamental analytical theory for fuzzy PID controller is not available.
Motivated by previous discussion, an analytical tuning method was proposed to design a fuzzy PID controller used in Smith predictor. The robustness of the fuzzy PID controller was analyzed. This fuzzy PID-based Smith predictor has good robustness such that it can deal with more uncertainty than conventional PID controller. The parameters of the fuzzy PID controller can be derived by using Lyapunov theory.
2 Problem formulation
2.1 Smith predictor
Smith predictor controller, as shown in Fig.1, can be divided into two parts: the primary controller C and the predictor structure [5]. In this figure, P is the plant; P0 is the model without delay time; r is the reference input; e is the signal error; y is the output of a industrial process; u is the control action; q is the disturbance; 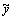 is the output of the model of the industrial process;
is the output of the model of the industrial process; 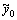 is the output of the model without delay time; Ln is the actual time delay; and s is the frequency domain.
is the output of the model without delay time; Ln is the actual time delay; and s is the frequency domain.
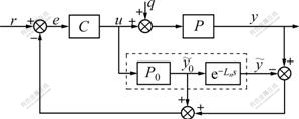
Fig.1 Schematic diagram of Smith predictor controller
Primary controller C is a PID controller or a fuzzy PID controller. A PID controller is described by the following transfer function [13]:
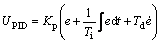 (1)
(1)
where UPID is the control signal acting on the signal errore; Kp is the proportional gain; Ti and Td are integral time constant and derivative time constant, respectively.
The predictor (dotted portion in Fig.1) is composed of a model of the plant without dead time (P0) and a model with dead time 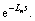 The dead time is eliminated from the closed-loop characteristic equation under an ideal situation. Thus, the Smith predictor can suppress effects that are caused by delay time [11].
The dead time is eliminated from the closed-loop characteristic equation under an ideal situation. Thus, the Smith predictor can suppress effects that are caused by delay time [11].
However, the Smith predictor requires an accurate model of the controlled object. In industrial process control, the accurate model cannot be obtained. Thus, if controller C is not appropriately chosen, small uncertainties could drive the system to instability [5].
2.2 Fuzzy PID controller
The structure of a fuzzy PID controller is shown in Fig.2, which combines the features of both fuzzy-PD and the fuzzy-PI controllers.

Fig.2 Schematic diagram of fuzzy PID controller
When there are infinite rules, the output model of the rule base is given as follows [14-15]:
U=uL+uN (2)
with
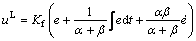 (3)
(3)
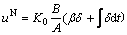 (4)
(4)
where uL is the nominal linear item; uN is the nonlinear compensation item; Kf=KeK0(α+β)B/A; α=Kd/Ke; β=K1/K0; σ=Ke(e+ α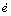 ); Ke=1/|emax| and Kd are input gains; A and B are half supports of input membership function and out membership function, respectively; γ is a nonlinear time-varying parameter (2/3≤γ≤1); and δ=A(1-γ)σ is a nonlinear function.
); Ke=1/|emax| and Kd are input gains; A and B are half supports of input membership function and out membership function, respectively; γ is a nonlinear time-varying parameter (2/3≤γ≤1); and δ=A(1-γ)σ is a nonlinear function.
3 Tuning of fuzzy-PID controller
3.1 Sliding-mode property
Eq.(2) can be rewritten as [14]:
U=Ue+U * (5)
with
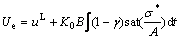 (6)
(6)
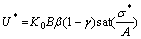 (7)
(7)
where 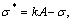 and sat(?) is the saturation function.
and sat(?) is the saturation function.
Eq.(5) is actually a sliding mode type controller. Ue is an estimated equivalent control, and U* is a switching control law [16].
3.2 Plant model
The plant is often described by the first order plus delay time (FOPDT) that is one of the most common and adequate ones used, especially in the process control industries [17-19]. The transfer function of the FOPDT is given by
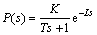 (8)
(8)
where K, T and L are the steady-state gain, the time constant, and the time delay of the model, respectively. The estimation of these parameters using step response method, frequency response, and closed-loop relay feedback, is well described.
Suppose that there is a modeling error, the plant model is given by
 (9)
(9)
where  denotes the mathematical model of P(s), and P0(s) denotes no delay time part.
denotes the mathematical model of P(s), and P0(s) denotes no delay time part.
3.3 Tuning
Using first-order Padé approximation, one can obtain
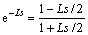 (10)
(10)
Integrating Eqs.(8) and (10), input u and output y can be approximated by the following ordinary differential equation (ODE):
 (11)
(11)
where

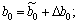

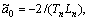


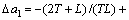

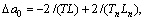
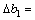
 .
.
Similarly, input u with outputs 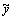 and
and  can be respectively expressed by
can be respectively expressed by
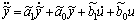 (12)
(12)
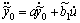 (13)
(13)
where  and
and  .
.
From Fig.1, error e is given as
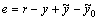 (14)
(14)
Integrating Eqs.(11)-(14), one can obtain
 (15)
(15)
where
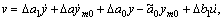
 .
.
By substituting Eq.(2) into Eq.(15), Eq.(15) can be rewritten as

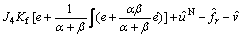 (16)
(16)
where

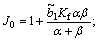
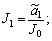
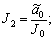

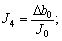


It is assumed that 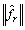 <F0 and
<F0 and 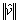 <V0 with F0 and V0 are finite positive numbers, respectively.
<V0 with F0 and V0 are finite positive numbers, respectively.
Let 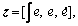 Eq.(16) can be transformed as
Eq.(16) can be transformed as
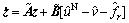 (17)
(17)
where
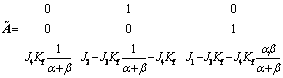
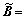 [0 0 1]T
[0 0 1]T
Theorem 1: If parameters K0, Ke, α, β, B and A in the fuzzy PID controller are chosen as in Eq.(17) so that matrix 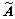 is stable, the error dynamics (Eq.(16)) driven by controller (2) is globally asymptotically stable.
is stable, the error dynamics (Eq.(16)) driven by controller (2) is globally asymptotically stable.
The proof of the theorem can be seen in Ref.[12].
4 Robustness analysis
A Lyapunov function at the kth layer can be chosen as
 (18)
(18)
The derivative of V(σ) is given as
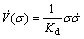 (19)
(19)
with


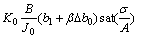 (20)
(20)
Matrix 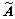 is stable when parameters are properly designed based on previous theorem. Thus, control error e is bounded, which means that Ue can compensate most of the undesirable effects [20]. Then, the following inequality exists:
is stable when parameters are properly designed based on previous theorem. Thus, control error e is bounded, which means that Ue can compensate most of the undesirable effects [20]. Then, the following inequality exists:
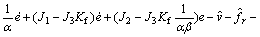
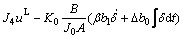 ≤F (21)
≤F (21)
where F is a finite positive number.
By using the ideal function 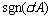 instead of the approximation
instead of the approximation 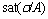 in Eq.(20), Eq.(19) can be expressed as follows:
in Eq.(20), Eq.(19) can be expressed as follows:
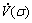 ≤
≤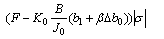 (22)
(22)
If the control at every layer can be determined so that
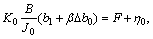
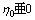 (23)
(23)
then the closed-loop system stability is guaranteed by
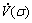 ≤
≤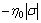 (24)
(24)
From Eq.(24), the control system is globally asymptotically stable.
Remark 1: From Eq.(24), the robustness of fuzzy and conventional PID controllers is equal to F=0. However, the robustness of fuzzy PID controller is better than that of conventional PID controller as F>0.
5 Simulations
In this section, three examples were used to test the proposed tuning method.
Example 1: Suppose that an industrial is described by
 (25)
(25)
In the primary controller, the parameters of the fuzzy and conventional PID controllers were designed using the same method. Their values are given in Tables 1 and 2, respectively.
When there is no modeling error, i.e.,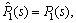 the performance is shown in Fig.3, where there exists an obvious difference between the fuzzy PID controller and conventional PID controller. However, when there exists modeling error, i.e.,
the performance is shown in Fig.3, where there exists an obvious difference between the fuzzy PID controller and conventional PID controller. However, when there exists modeling error, i.e.,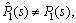 the control performance is shown in Fig.4, where the fuzzy PID control is stable, but the conventional PID control is unstable.
the control performance is shown in Fig.4, where the fuzzy PID control is stable, but the conventional PID control is unstable.
Table 1 Parameters of fuzzy PID controller for P1(s)

Table 2 Parameters of conventional PID controller for P1(s)

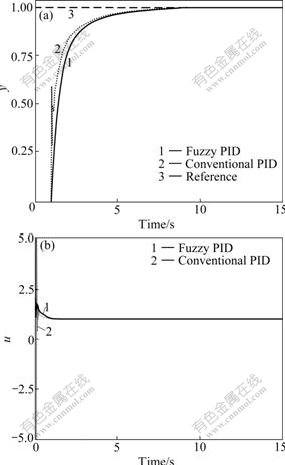
Fig.3 PID control performance for P1(s) without modeling error: (a) Control performance; (b) Control action
Example 2: Assume that an industrial process is described by the following high order model:
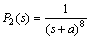 (26)
(26)
where a=1. Suppose that there is no modeling error in process (26). Based on step response and Nyquist curves of industrial process (26), the approximation model can be obtained as follows:
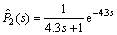 (27)
(27)
The parameters of the fuzzy and conventional PID controllers are shown in Tables 3 and 4, respectively. The control performances of the fuzzy and the conventional PID controllers are shown in Fig.5. The overshoot of the
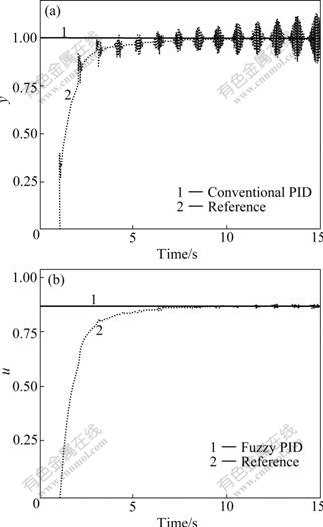
Fig.4 PID control performance for P1(s) with modeling error: (a) Control performance; (b) Control action
Table 3 Parameters of fuzzy PID controller for P2(s)

Table 4 Parameters of conventional PID controller for P2(s)

fuzzy PID control is lower than that of the conventional PID controller. Moreover, the PID control has impulse signal that may destroy instrument.
Example 3: Assume that an industrial process is described by
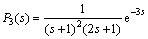 (28)
(28)
Its approximate model is described by the following equation using traditional identification method [1]:
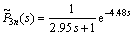 (29)
(29)
The parameters of fuzzy and conventional PID controllers are shown in Tables 5 and 6, respectively.

Fig.5 PID control performance for P2(s) without modeling error: (a) Control performance; (b) Control action
Table 5 Parameters of fuzzy PID controller for P3(s)

Table 6 Parameters of conventional PID controller for P3(s)

In this situation, assume that there is an input saturation, i.e., the input u∈[-1.5, 1.5]. The control performance is shown in Fig.6, where the overshoot of the fuzzy PID controller is lower than that of the conventional PID controller.
6 Conclusions
(1) An analytical tuning of the fuzzy PID controller for Smith predictor is presented. Based on Lyapunov theory, the Smith predictor is analyzed in time domain. The parameters of the fuzzy PID controller can be obtained using traditional linear control theory and sliding mode control theory.
(2) The control performance of the fuzzy PID controller is better than that of the conventional PID controller.
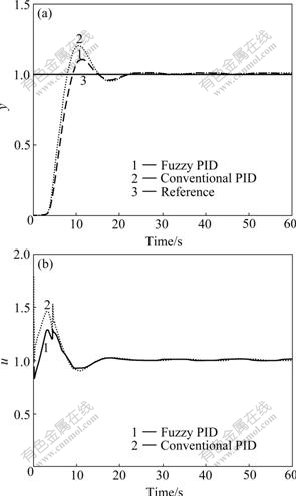
Fig.6 Control performance for P3(s): (a) Control performance; (b) Control action
(3) The robustness of fuzzy PID controller is better than that of conventional PID controller because the fuzzy PID controller has property of sliding mode control.
(4) The fuzzy PID controller is more stable than the conventional PID controller based on equation analysis and simulation results.
References
[1] KAYA I. IMC based automatic tuning method for PID controllers in a Smith predictor configuration [J]. Computers and Chemical Engineering, 2004, 28(3): 281-290.
[2] CAMACHO O, FRANCISCO D L C. Smith predictor based-sliding mode controller for integrating processes with elevated dead-time [J]. ISA Transactions, 2004, 43: 257-270.
[3] CHEN Ning, LIU Wei-ying, GUI Wei-hua. Delay-dependent decentralized robust control for power systems based on output feedback [J]. J Cent South Univ: Science and Technology, 2009, 40(3): 711-718. (in Chinese)
[4] RONG Hui-gui, ZHOU Ning, JIN Min, WU Jia-xin. Research on service-oriented framework of interface prototype driven development [C]// The 1st IEEE Inter Conf on Computer Science and Software Engineering. Wuhan, 2008: 552-557.
[5] NORMEY J E, CAMACHO E F. Dead time compensators: A survey [J]. Control Engineering Practice, 2008, 16(4): 407-428.
[6] ZHANG Guang-hui, QIAN Feng, SHAO Hui-he. Robust tuning method for modified Smith predictor [J]. Journal of Systems Engineering and Electronics, 2007, 18(1): 89-94.
[7] GEORGE K I M, HU B G, RAYMOND G G. Analysis of direct action fuzzy PID controller structures [J]. IEEE Trans Syst, Man, Cybern B, 1999, 29(3): 371-388.
[8] LI H X, TSO S K. Quantitative design and analysis of fuzzy PID control: A step towards autotuning [J]. International Journal of Systems Science, 2000, 31(5): 545-553.
[9] GEORGE K I M, HU B G, RAYMOND G G. Two-level tuning of fuzzy PID controllers [J]. IEEE Trans Syst, Man, Cybern B, 2001, 31(2): 263-269.
[10] RAO A S, CHIDAMBARAM M. Analytical design of modified smith predictor in a two-degrees-of-freedom control scheme for second order unstable processes with time delay [J]. ISA Transactions, 2008, 47: 407-419.
[11] CHIEN I L, PENG S C, LIU J H. Simple control method for integrating processes with long dead-time [J]. Journal of Process Control, 2002, 12(2): 391-404.
[12] WANG Yu-ying, ZHOU Xing-she. Fuzzy-Smith control for QoS- adaptive notification service [J]. Lecture Notes in Computer Science, 2007, 46(11): 1140-1147.
[13] LI Y, HEONG K, CHONG G C Y. PID control system analysis and design [J]. IEEE Control Systems, 2006, 26(1): 32-41.
[14] DUAN Xiao-gan, LI Han-xiong, DENG Hua. An effective tuning method for fuzzy PID with internal model control [J]. Industrial and Engineering Chemistry Research, 2008, 47(21): 8317-8323.
[15] LI H X, GATLAND H. Conventional fuzzy logic control and its enhancement [J]. IEEE Trans Syst, Man, Cybern B, 1996, 26(10): 791-797.
[16] EDWARDS C, SPURGEN S K. Sliding mode control: Theory and applications [M]. London: Taylor & Francis Ltd, 1998: 1-30.
[17] ASTROM K J, HAGGLUND T. The future of PID control [J]. Control Engineering Practice, 2001, 9: 1163-1175.
[18] LI Y, KIAM H A, GREGORY C Y. Patents, software and hardware for PID Control [J]. IEEE Control Systems Magazine, 2006, 26(1): 42-54.
[19] HAN J Q. Form PID to active disturbance rejection control [J]. IEEE Transaction on Industrial Electronics, 2009, 56(3): 900-906.
[20] LI H X, GATLAND B H, GREEN A W. Fuzzy variable structure control [J]. IEEE Trans Sys, Man, Cybern B, 1997, 27(2): 306- 312.
Foundation item: Project(70473068) supported by the National Natural Science Foundation of China; Project(05JZD00024) supported by the Major Subject of Ministry of Education, China
Received date: 2010-01-04; Accepted date: 2010-04-01
Corresponding author: RONG Hui-gui, Doctoral candidate; Tel: +86-731-88828148; E-mail: ronghg@163.com
(Edited by CHEN Wei-ping)