Trans. Nonferrous Met. Soc. China 23(2013) 2905-2913

Plastic yielding of NiTi shape memory alloy under local canning compression

Shu-yong JIANG¹, Li HU², Ya-nan ZHAO¹, Yan-qiu ZHANG¹, Yu-long LIANG²

1. Industrial Training Centre, Harbin Engineering University, Harbin 150001, China;

2. College of Materials Science and Chemical Engineering, Harbin Engineering University, Harbin 150001, China

Received 12 September 2012; accepted 7 November 2012

Abstract: As a new attempt, local canning compression was applied in order to implement large plastic deformation of nickel-titanium shape memory alloy (NiTi SMA) at room temperature. The plastic mechanics of local canning compression of NiTi SMA was analyzed according to the slab method as the well as plastic yield criterion. Transmission electron microscopy (TEM), high resolution transmission electron microscopy (HRTEM) and scanning electron microscopy (SEM) were used to study the microstructural evolution as well as deformation behavior of NiTi samples under local canning compression. Increasing the hydrostatic pressure with the increase in the outer diameters of the steel cans is responsible for suppressing the initiation and growth of the micro-cracks, which contributes to enhancing the plasticity of NiTi SMA and avoiding the occurrence of brittle fracture. Plastic deformation of NiTi SMA under a three-dimensional compressive stress state meets von-Mises yield criterion at the true strains ranging from about 0.15 to 0.50, while in the case of larger plastic strain, von-Mises yield criterion is unable to be met since the amorphous phase arises in the deformed NiTi sample.

Key words: NiTi alloy; shape memory alloy; yield criterion; plastic deformation; plastic mechanics

1 Introduction

The remarkable attractiveness of nickel-titanium shape memory alloy (NiTi SMA) comes from its shape memory effect as well as superelasticity [1]. Chemical composition, heat treatment and plastic working history of NiTi SMA have a significant influence on its shape memory effect as well as superelasticity [2-7]. In particular, cold plastic deformation plays an important role in enhancing the mechanical properties and the functional properties of NiTi SMA [8,9]. Severe plastic deformation (SPD) based on the cold working is able to lead to a mixture of nanocrystalline and amorphous phase or a complete amorphization of NiTi SMA. Furthermore, the appropriate heat treatment contributes to nanocrystallization of amorphous NiTi SMA subjected to SPD, which is responsible for the mechanical properties and the functional properties of NiTi SMA. For example, SERGUEEVA et al [10] investigated amorphization of NiTi SMA based on SPD by HPT as well as nanocrystallization of amorphous NiTi SMA in the case of annealing, which causes NiTi SMA to possess an ultimate tensile strength of 2650 MPa at room temperature and the maximum elongation of more than 200% at 500 °C [10]. DELVILLE et al [11] applied heat treatment by pulsed electric current for obtaining nanocrystallization of amorphous NiTi wire based on cold drawing and consequently found that the NiTi wire with nanocrystalline regions exhibits the exceptional cyclic stability and possesses the perfect superelasticity with a recoverable strain of 8%. Accordingly, many researchers have devoted themselves to SPD of NiTi SMA based on cold working, such as high pressure torsion (HPT) [12-14], cold rolling [15-17] and surface mechanical attrition treatment (SMAT) [18-20]. HPT is able to induce much higher strain by means of a shear deformation and can lead to a complete amorphization of NiTi SMA. As compared with HPT, cold rolling and cold drawing can induce the relatively lower plastic strain and thus lead to partial amorphization and nanocrystallization of NiTi SMA. SMAT is capable of producing a surface layer with a mixture of nanocrystalline and amorphous phase by inducing severe plastic strain on the surface of NiTi SMA.

In the present study, as a new attempt to generate SPD, local canning compression was used for fabricating amorphous and nanocrystalline NiTi SMA at room temperature. The plastic mechanics of local canning compression of NiTi SMA was solved and the yield criterion of NiTi SMA under a three-dimensional compressive stress state was investigated, which has never been reported so far.

2 Experimental

The NiTi alloy with a nominal composition of Ni_50.9Ti_49.1 (mole fraction, %) was prepared by vacuum induction melting method, and was then rolled at 800 °C, and finally was drawn to the NiTi bar with a diameter of 12 mm at 400 °C. Transformation temperatures of the NiTi bar were measured by differential scanning calorimetry (DSC) at the heating or cooling rate of 10 °C/min, which were as follows: M_s=-27.2 °C, M_f=-41.7 °C, A_s=-17.3 °C, A_f =-4.1 °C. Therefore, the NiTi bar possessed the B2 austenite structure at room temperature. The NiTi samples with the diameter of 4 mm and the height of 6 mm were cut from the NiTi bar by means of electro-discharge machining (EDM) and then were locally inserted into the low carbon steel can with the inner diameter of 4 mm and the height of 3 mm. The outer diameters of the steel can were 6, 8, 10, 12, 14, 16, 18 and 20 mm, respectively, as shown in Fig. 1. The canned NiTi samples were placed between the top anvil and the bottom one of the INSTRON-5500R equipment and were then compressed under a three-dimensional compressive stress state at a strain rate of 0.05 s^-1 at room temperature, as shown in Fig. 2. The perfect lubrication is performed between the NiTi samples and the anvils.

Fig. 1 Photographs of locally canned NiTi samples

Fractographs for the compressed NiTi sample were examined by scanning electron microscopy (SEM) using FEI Quanta200 microscope and optical microscopy. Microstructures were characterized by transmission electron microscopy (TEM) and high resolution transmission electron microscopy (HRTEM) using FEI TECNAI G2 F30 microscope with a side-entry and double-tilt specimen stage with angular ranges of ±40° at an accelerating voltage of 300 kV. Foils for TEM observation were mechanically ground to 70 μm and then thinned by twin-jet polishing in an electrolyte consisting of 6% HClO₄, 34% C₄H₁₀O and 60% CH₃OH in volume fraction.

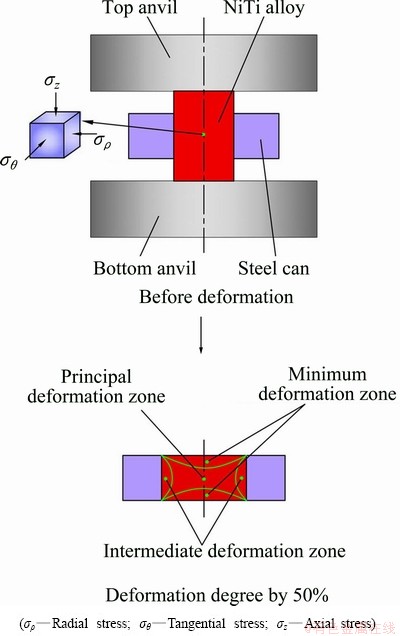
Fig. 2 Schematic diagram of local canning compression of NiTi SMA

3 Analysis of mechanics of local canning compression of NiTi alloy

The mechanical model of local canning compression of NiTi sample can be divided into two parts. One part is shown in Fig. 3, where the steel can belongs to plastic deformation under the action of the pressure p. The other part is shown in Fig. 4, where the cylindrical NiTi sample can be regarded as the compressive deformation within the boundary condition of the pressure p as well as without friction. The pressure p will become the bridge across which the mechanics problem of local canning compression of NiTi sample is able to be solved with the assumption that the steel can has no strain hardening and the dimension change of its inner and outer diameters has a negligible influence on the pressure p during the plastic deformation. Therefore, the plastic mechanics of local canning compression of NiTi alloy can be solved by combining slab method with plastic yield criterion.

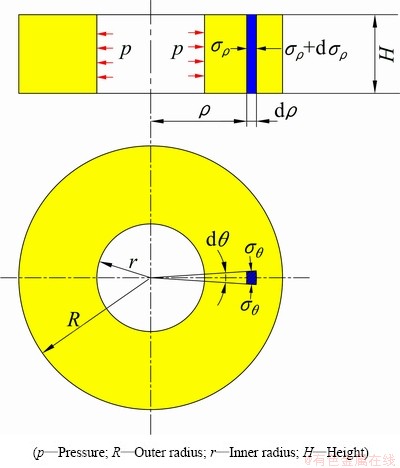
Fig. 3 Schematic diagram of mechanical model of steel can

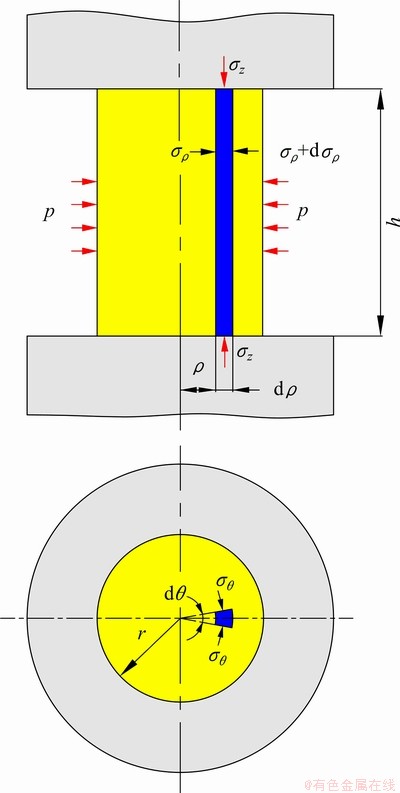
Fig. 4 Schematic diagram of mechanical model of NiTi sample (h—Height of NiTi sample)

3.1 Analysis of plastic mechanics of steel can under pressure

As shown in Fig. 3, the mechanics of plastic deformation of the steel can under the inner pressure p belongs to the axisymmetrical problem as well as the plane stress problem, where σ_z is equal to zero without the axial loading, while σ_ρ and σ_θ are irrespective to the z coordinate axis. Simultaneously, it is assumed that the total material particles within the steel can are all subjected to plastic deformation. In addition, σ_ρ and σ_θ are both the principal stresses due to no shear stresses in the steel can. By intercepting an element slab in the steel can, the equilibrium differential equation along the radial direction is obtained as follows.

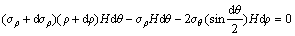    (1)

By ignoring the high-order items of Eq. (1), the following equation can be obtained:

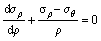                              (2)

Because the steel can meets the von-Mises yield criterion,

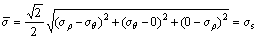    (3)

Equation (3) can lead to the following equation:

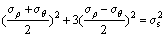                  (4)

By selecting the angle α as the parameter variable, Eq. (4) can be expressed by

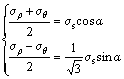                         (5)

σ_ρ and σ_θ can be expressed by the parameter α, so Eq. (5) can be further converted to the following expression:

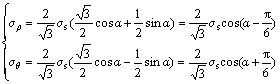 (6)

Equation (6) is the plastic yield condition described by the parameter α and thus it can be geometrically expressed by the ellipse as shown in Fig. 5.

Substitution of Eq. (6) into Eq. (2) leads to

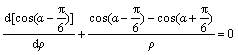      (7)

The simplification of Eq. (7) results in

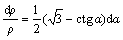                         (8)

By integrating Eq. (8), the following expression can be obtained.

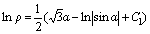                     (9)

where C₁ is the integral constant.

According to the boundary condition: ρ=R, σ_ρ=0, there is

                               (10)

In the range from -π to +π, 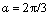or  meets Eq. (10). However, when 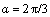, σ_θ<0; when  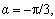σ_θ>0. Furthermore, when all the total material particles within the steel can are in the plastic yield state, there only exists σ_θ>0 at the boundary of ρ=R. Therefore,  is the boundary condition which meets Eq. (10).

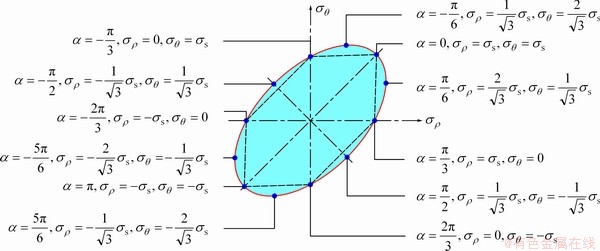
Fig. 5 Geometric diagram of plastic yield condition

By substituting and ρ=R into Eq. (9), the following expression can be obtained.

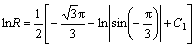             (11)

Then, the integral constant C₁ can be determined as

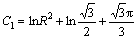                      (12)

Substitution of the integral constant C₁ into Eq. (9) results in

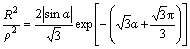              (13)

The stress distribution in the steel can along the radial direction can be solved by combining Eq. (6) with Eq. (13).

By substituting the boundary condition of ρ=r and σ_ρ=-p (p is the positive value) into Eq. (6) and Eq.(13), Eq. (14) can be obtained as follows.

             (14)

Equation (14) represents the relationship between the pressure p and the specific value R/r. Equation (14) is the expression to obtain the accurate solution of the pressure p, where the parameter α ranges from -π/3 to -5π/6 according to Fig. 5.

The curve of the relationship between the pressure p and the specific value R/r can be obtained according to Eq. (14), as shown in Fig. 6. It can be seen from Fig. 6 that the pressure p increases with the increase of the specific value R/r. Therefore, establishing the various R/r values is capable of resulting in the various pressure which acts on the NiTi sample. However, the pressure is unable to increase infinitely with the specific value R/r, because the specific value R/r in Eq. (14) has a limited range from 1 to 2.9615 according to the parameter α ranging from -π/3 to -5π/6. As shown in Fig. 5, when α=-2π/3, σ_θ=0, and thus R/r=2.4766. When R/r<2.4766, σ_θ belongs to the tensile stress in the total steel can. On the other hand, according to

,

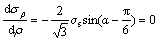α=-5π/6 can be obtained and thus σ_ρ has the extremum 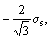where R/r=2.9615.

Therefore, when 2.4766< R/r< 2.9615, there exists the transition layer of σ_θ=0 in the steel can where σ_θ belongs to the compressive stress in the transition layer and σ_θ belongs to the tensile stress around the transition layer. When R/r>2.9615, the plastic deformation zone will be surrounded by the elastic deformation zone in the steel can and thus Eq. (14) is unavailable.

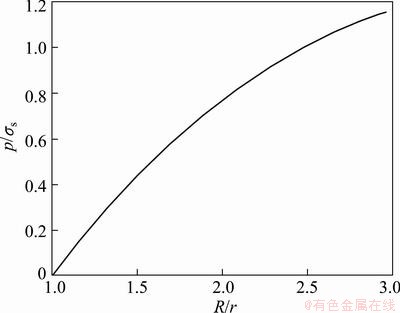
Fig. 6 Curve of p/σ_s vs R/r

3.2 Analysis of mechanics of NiTi sample under pressure

As shown in Fig. 4, the mechanical model of NiTi sample under compression belongs to the axisymmetrical problem as well. Furthermore, the influence of the friction on the compressive deformation of NiTi sample is ignored because the perfect lubrication can be performed between the NiTi sample and the anvil. An element slab is intercepted in the NiTi sample and the equilibrium differential equation along the radial direction is obtained as follows.

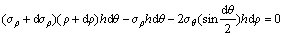    (15)

By ignoring the high-order items of Eq. (15), the following equation can be obtained:

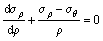                           (16)

As for the radial strain ε_ρ and the tangential strain ε_θ in the NiTi sample, the following expression can be established:

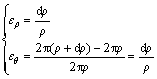                   (17)

According to Eq. (17), the relationship between the radial strain ε_ρ and the tangential strain ε_θ is expressed by

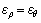                                    (18)

Based on the constitutive relationship between the stress and the strain, the relationship between the radial stress σ_ρ and the tangential stress σ_θ is expressed by

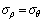                                    (19)

By combining Eq. (16) with Eq. (19), the following expression can be obtained.

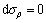                                   (20)

Integrating Eq. (20) results in

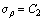                                    (21)

where C₂ is the integral constant and can be determined as C₂=p according to the boundary condition of ρ=r, σ_ρ=-p, so σ_ρ is expressed as

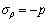                                   (22)

Equation (22) reveals that the radial stress σ_ρ is always equal to the pressure p in the compressive deformation of NiTi sample. Furthermore, the axial stress σ_z can be measured by the stress—strain curves under compressive deformation. The effective stress 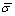 of the material particles in the deformation zone of the NiTi sample under compression can be calculated as

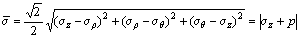    (23)

Furthermore, the effective strain 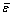 of the material particles in the deformation zone of the NiTi sample under compression can be calculated as

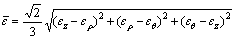      (24)

4 Results and discussion

4.1 Mechanical behavior of NiTi sample under local canning compression

Figure 7 indicates the compressive stress—strain curves of the NiTi sample with various outer diameters (D) of the steel can. It can be clearly seen from Fig. 7 that compared with the uncanned NiTi sample, the compressive stress—strain curves of the canned NiTi samples keep the similar shape, where the NiTi alloy experiences the four stages including the elastic deformation of the austenite phase, the stress-induced martensite phase transformation, the elastic deformation of the stress-induced martensite and the plastic deformation of the stress-induced martensite. Furthermore, the compression stress σ_z increases with the increase of the outer diameters of the steel can. The stress σ_z increases slightly at the previous three stages where the mechanical behavior and the phase transformation behavior of the locally canned NiTi alloy under a three-dimensional compressive stress state is out of the scope of the paper and will be investigated in the future. However, during the plastic deformation of NiTi alloy, the stress σ_z increases sharply with the increase of the outer diameters of the steel can when the outer diameter of the metal can is less than 12 mm, but it increases slightly when the outer diameter of the steel can is greater than 12 mm. When the outer diameter of the steel can is 6, 8 or 10 mm, the value of R/r is less than 2.9615, so that all the material points in the steel can meet the plastic yield criterion and the pressure p can be solved according to Eq. (14). When the outer diameter of the steel cans is 12, 14, 16, 18 or 20 mm, the value of R/r is greater than 2.9615, so that not all the material points in the metal can meet the plastic yield criterion and the pressure p is unable to be solved according to Eq. (14). In general, when the value of R/r is greater than 2.9615, the mechanical state of the steel can under the action of the pressure p probably falls into two situations, as shown in Fig. 8. On one hand, the steel can consists of the plastic zone and the elastic zone, where the plastic zone is surrounded by the elastic zone. On the other hand, when the value of R/r increases to a certain value, the steel consists of the plastic zone, the elastic zone and the rigid zone, where the plastic zone is surrounded by the elastic zone and the elastic zone is surrounded by the rigid zone. Especially for the situation as shown in Fig. 8 (b), the infinite increase of the R/r value is unable to lead to considerable increase in the pressure p.

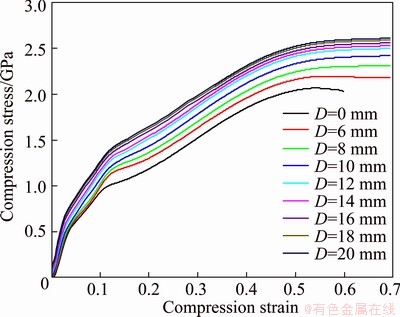
Fig. 7 Stress—strain curves of locally canned NiTi sample at reduction in height by 50% (D=0 represents uncanned NiTi sample)

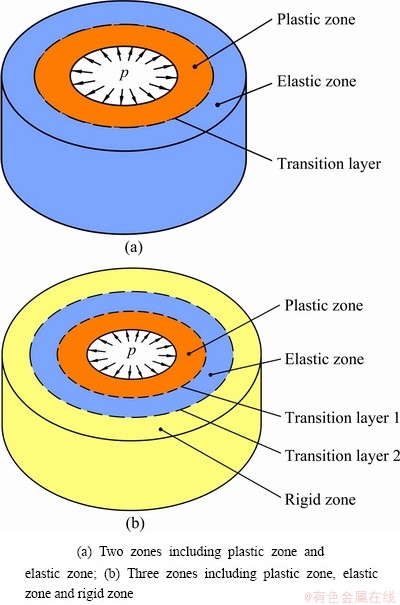
Fig. 8 Schematic diagram of deformation zones of steel can with R/r>2.9615

Figure 9 shows the equivalent stress—equivalent strain curves of the NiTi samples under local canning compression in accordance with Eq. (23) and Eq. (24), where the stress σ_z is derived from the stress—strain curves in Fig. 7 and the p value results from Eq. (14) in which the yield strength σ_s of the steel can is measured as 250 MPa. It can be seen from Fig. 9 that the plastic deformation of the locally canned NiTi samples under a three-dimensional compressive stress meets the von-Mises yield criterion at the true strains ranging from 0.15 to 0.50. When the true strain is less than 0.15, the NiTi sample will experience initial elastic deformation and subsequent stress-induced martensite phase transformation. When the true strain is greater than 0.50, NiTi sample is subjected to so large plastic deformation leading to its amorphization or nanocrystallization that it is unable to meet the von-Mises yield criterion.

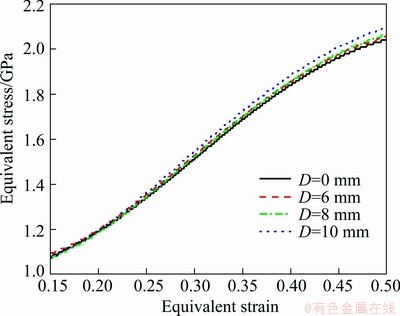
Fig. 9 Equivalent stress—equivalent strain curves of NiTi samples under local canning compression

Figure 10 shows the relationship of the hydrostatic stress σ_h of the NiTi sample under local canning compression with respect to the specific value R/r of the steel can. The hydrostatic pressure σ_h is calculated according to the following expression:

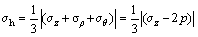             (25)

where the stress σ_z is derived from Fig. 7 and is imparted to a negative one, and the p value is derived from Eq. (14). As shown in Fig. 10, the hydrostatic pressure σ_h increases with the increase of the outer diameter of the steel can. Therefore, the increase of the specific value R/r leads to the increase of the pressure p and consequently further results in the increase of the hydrostatic pressure σ_h, which contributes to the considerable enhancement of plasticity of the NiTi alloy.

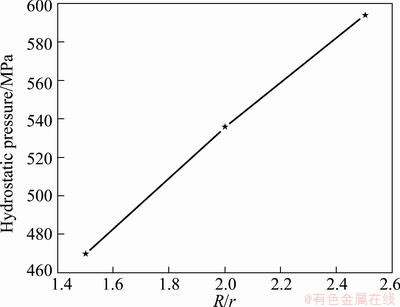
Fig. 10 Relationship between hydrostatic pressure and R/r of steel can

4.2 Microstructural observation of NiTi alloy under local canning compression

According to the previous mechanics analysis, the local canning compression of NiTi alloy causes it in a three-dimensional compressive stress state, which is responsible for suppressing the initiation and growth of the micro-cracks. Furthermore, increasing the outer diameters of the steel can contributes to enhancing the hydrostatic pressure, which plays a significant role in a large plastic deformation of NiTi alloy and has been validated by the compressive experiments. As for the uncanned NiTi sample, when the reduction in height arrives up to 40%, the NiTi sample exhibits a typical characteristic of brittle fracture along with the transcrystalline fracture, as shown Fig. 11. However, for all the canned NiTi samples with the diameters of the steel ranging from 6 mm to 20 mm, the reduction in height by 50% leads to no fracture of the NiTi samples.

In order to further understand plastic deformation mechanism of NiTi sample under local canning compression, microstructural evolution in the principal deformation zone of NiTi alloy is investigated.

Figure 12 shows the TEM images and the selected area electron diffraction pattern (SAEDP) of the as-received NiTi bar. It can be seen from Fig. 12 that the as-received NiTi bar is characterized by a coarse grain and is composed of a typical B2 austenite phase and a little Ti₂Ni phase. Figure 13 shows the TEM images, the SAEDP, the HRTEM image and the corresponding fast Fourier transform (FFT) of the NiTi sample subjected to the reduction in height by 50%. It can be found from Fig. 13 that the plastic deformation at the reduction in height by 50% provides a certain driving force to induce the occurrence of the nanocrystalline phase along with an extremely small amount of amorphous phase. In addition, the stacking faults, the dislocations and the twins occur in the retained nanocrystalline phase, which reveals that the deformation twinning and dislocation slip play an important role in nanocrystallization and amorphization of NiTi alloy.

Fig. 11 Fractograph of uncanned NiTi alloy under compression

5 Conclusions

1) Local canning compression of NiTi alloy causes it in a three-dimensional compressive stress state, which contributes to suppressing the initiation and growth of the micro-cracks and thus enhancing the plasticity of NiTi alloy. The analytical and experimental results reveal that increasing the outer diameters of the steel can contributes to enhancing the hydrostatic pressure, which lays the mechanical foundation for severe plastic deformation of NiTi SMA, and there exists the critical outer diameter of the steel can, beyond which increasing the outer diameter of the steel can is unable to enhance the hydrostatic pressure substantially.

2) Local canning compression of NiTi alloy meets the von-Mises yield criterion at the true strains ranging from 0.15 to 0.50. When the true strain is less than 0.15, the NiTi sample will experience initial elastic deformation and subsequent stress-induced martensite phase transformation. When the true strain is greater than 0.50, NiTi sample is subjected to so severe plastic deformation leading to its nanocrystallization or amorphization that it is unable to meet the von-Mises yield criterion.

3) Local canning compression provides a new approach to implementing large plastic deformation of NiTi alloy. Plastic deformation at the reduction in height by 50% provides a certain driving force to induce the occurrence of the nanocrystalline phase along with an extremely small amount of amorphous phase. Furthermore, deformation twinning and dislocation slip play an important role in nanocrystallization and amorphization of NiTi alloy.

Fig. 12 TEM images of as-received NiTi alloy

Fig. 13 Microphotographs of NiTi sample subjected to plastic deformation at reduction in height by 50%

References

[1] OTUKA K, REN X. Physical metallurgy of Ti-Ni-based shape memory alloys [J]. Progress in Materials Science, 2005, 50(5): 511-678.

[2] MEHRABI K, BAHMANPOUR H, SHOKUHFAR A, KNEISSL A. Influence of chemical composition and manufacturing conditions on properties of NiTi shape memory alloys [J]. Materials Science and Engineering A, 2008, 481-482: 693-696.

[3] JIANG Shu-yong, ZHANG Yan-qiu. Microstructure evolution and deformation behavior of as-cast NiTi shape memory alloy under compression [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(1): 90-96.

[4] JIANG Shu-yong, ZHANG Yan-qiu, FAN Hong-tao. Fracture behavior and microstructure of as-cast NiTi shape memory alloy [J]. Transactions of Nonferrous Metals of Society of China, 2012, 22(6): 1401-1406.

[5] ZHANG Yan-qiu, JIANG Shu-yong, ZHAO Ya-nan, TANG Ming. Influence of cooling rate on phase transformation and microstructure of Ti-50.9%Ni shape memory alloy [J]. Transactions of Nonferrous Metals of Society of China, 2012, 22(11): 2685-2690.

[6] KE C B, CAO S S, MA X, ZHANG X P. Modeling of Ni₄Ti₃ precipitation during stress-free and stress-assisted aging of bi-crystalline NiTi shape memory alloys [J]. Transactions of Nonferrous Metals of Society of China, 2012, 22(10): 2578-2585.

[7] SONG J, WANG L M, ZHANG X N, SUN X G, JIANG H, FAN Z G, XIE C Y, WU M H. Effects of second phases on mechanical properties and martensitic transformations of ECAPed TiNi and Ti-Mo based shape memory alloys [J]. Transactions of Nonferrous Metals of Society of China, 2012, 22(8): 1839-1848.

[8] ZHENG Y F, HUANG B M, ZHANG J X, ZHAO L C. The microstructure and linear superelasticity of cold-drawn TiNi alloy [J]. Materials Science and Engineering A, 2001, 279(1-2): 25-35.

[9] MITWALLY M E, FARAG M. Effect of cold work and annealing on the structure and characteristics of NiTi alloy [J]. Materials Science and Engineering A, 2005, 519(1-2): 155-166.

[10] SERGUEEVA A V, SONG C, VALIEV R Z, MUKHERJEE A K. Structure and properties of amorphous and nanocrystalline NiTi prepared by severe plastic deformation and annealing [J]. Materials Science and Engineering A, 2003, 339(1-2): 159-165.

[11] DELVILLE R, MALARD B, PILCH J, SITTNER P, SCHRYVERS D. Microstructure changes during non-conventional heat treatment of thin Ni-Ti wires by pulsed electric current studied by transmission electron microscopy [J]. Acta Materialia, 2010, 58(13): 4503-4515.

[12] KHMELEVSKAYA I Y, PROKOSHKIN S D, DOBATKIN S V, TATYANIN E V, TRUBITSYNA I B. Studies of composition, deformation temperature, pressure effects on structure formation in severely deformed TiNi-based shape memory alloys [J]. Materials Science and Engineering A, 2006, 438-440: 472-475.

[13] SINGH R, DIVINSKI S V, RNER H, PROKOFIEV E A, VALIEV R Z, WILDE G. Microstructure evolution in nanocrystalline NiTi alloy produced by HPT [J]. Journal of Alloys and Compounds, 2011, 509(S): S290-S293.

[14] PETERLECHNER M, WAITZ T, KARNTHALER H P. Nanocrystallization of NiTi shape memory alloys made amorphous by high-pressure torsion [J]. Scripta Materialia, 2008, 59(5): 566-569.

[15] TSUCHIYA K, INUZUKA M, TOMUS D, HOSOKAWA A, NAKAYAMA H, MORII K, TODAKA Y, UMEMOTO M. Martensitic transformation in nanostructured TiNi shape memory alloy formed via severe plastic deformation [J]. Materials Science and Engineering A, 2006, 438-440: 638-643.

[16] KIM Y H, CHO G B, HUR S G, JEONG S S, NAM T H. Nanocrystallization of a Ti–50.0Ni(at.%) alloy by cold working and stress/strain behavior [J]. Materials Science and Engineering A, 2006, 438-440: 531-535.

[17] SRIVASTAVA A K, SCHRYVERS D, HUMBEECK J V. Grain growth and precipitation in an annealed cold-rolled Ni_50.2Ti_49.8 alloy [J]. Intermetallics, 2007, 15(12): 1538-1547.

[18] MEI Q S, ZHANG L, TSUCHIYA K, GAO H, OHMURA T, TSUZAKI K. Grain size dependence of the elastic modulus in nanostructured NiTi [J]. Scripta Materialia, 2010, 63(10): 977-980.

[19] HU T, CHEN L, WU S L, CHU C L, WANG L M, YEUNG K W K, CHU P K. Graded phase structure in the surface layer of NiTi alloy processed by surface severe plastic deformation [J]. Scripta Materialia, 2011, 64(11): 1011-1014.

[20] HU T, CHU C L, Wu S L, XU R Z, SUN G Y, HUNG T F, YEUNG K W K, WU Z W, Li G Y, CHU P K. Microstructural evolution in NiTi alloy subjected to surface mechanical attrition treatment and mechanism [J]. Intermetallics, 2011, 19(8): 1136-114.

镍钛形状记忆合金在局部包套压缩下的塑性屈服

江树勇¹，胡 励²，赵亚楠¹，张艳秋¹，梁玉龙²

1. 哈尔滨工程大学 工程训练中心，哈尔滨 150001；

2. 哈尔滨工程大学 材料科学与化学工程学院，哈尔滨 150001

摘  要：作为一种崭新的尝试，局部包套压缩被应用于实现镍钛形状记忆合金在室温下的大塑性变形。基于主应力法和塑性屈服准则，分析了镍钛形状记忆合金局部包套的压缩塑性力学。采用透射电镜、高分辨透射电镜和扫描电镜研究镍钛形状记忆合金在局部包套压缩下的显微组织演变和变形行为。静水压力随着包套外径的增加而增加，有效地抑制了显微裂纹的萌生和扩展，有助于提高镍钛形状记忆合金的塑性，避免了脆性断裂的发生。在0.15~0.50的真实应变范围内，镍钛形状记忆合金在三向压应力状态下的塑性变形满足密席斯塑性屈服准则。在更大的塑性应变下，由于非晶相的出现，镍钛合金不能满足密席斯塑性屈服准则。

关键词：镍钛合金；形状记忆合金；屈服准则；塑性变形；塑性力学

(Edited by Xiang-qun LI)

Foundation item: Project (51071056) supported by the National Natural Science Foundation of China; Projects (HEUCF121712, HEUCF201317002) supported by the Fundamental Research Funds for the Central Universities of China

Corresponding author: Shu-yong JIANG; Tel: +86-451-82519706; E-mail: jiangshy@sina.com

DOI: 10.1016/S1003-6326(13)62813-7