用于大型地埋管换热器传热分析的绝热圆柱域模型

张方方¹，路伟¹，朱科¹，方肇洪¹，于明志^{1, 2}

(1. 山东建筑大学 热能工程学院，山东 济南，250101；

2. 山东省绿色建筑协同创新中心，山东 济南，250101)

摘要：地源热泵空调系统地埋管换热器由大量均匀分布钻孔换热器组成，其长期运行模拟的分析计算任务量大，为此，基于其地下土壤温度场分布特性和传热特性，提出绝热圆柱域模型，采用分离变量和叠加原理的方法得到土壤温度场和钻孔壁温解析解；采用已被广泛接受的有限长线热源模型和工程实测数据验证绝热圆柱域模型，比较不同负荷条件和钻孔数量时，2种模型计算得到的地埋管换热器20 a运行期内钻孔壁温。研究结果表明：对于大型地埋管换热器，绝热圆柱域模型与有限长线热源模型计算温度结果较一致，且埋管数量越多，误差越小；绝热圆柱域模型尤适用于埋管规模大于30个×30个的大型地源热泵系统的设计计算和分析；绝热圆柱域模型具有计算速度很快的特点，且其计算速度与埋管数量无关；采用绝热圆柱域模型进行埋管数量众多的大型地埋管换热器的设计计算不但具有较高准确度，而且可显著减少计算时间。

关键词：地源热泵；地埋管换热器；传热模型；解析解

中图分类号：TU83          文献标志码：A                开放科学(资源服务)标识码(OSID)

文章编号：1672-7207（2021）06-1915-09

Adiabatic cylindrical domain model for heat transfer analysis of large geothermal heat exchanger

ZHANG　Fangfang¹, LU Wei　¹, ZHU Ke　¹, FANG Zhaohong　¹, YU Mingzhi　^{1, 2}

(1. School of Thermal Engineering, Shandong Jianzhu University, Jinan 250101, China;

2. Co-Innovation Center for Green Building of Shandong Province, Jinan 250101, China)

Abstract: The main aim of this paper was to propose a method to cut down the calculation task of the long-term operation simulation of large geothermal heat exchangers(GHEs) of the ground source heat pump air conditioning system, which was composed of a large number of evenly distributed boreholes. Based on the characteristics of soil temperature distribution and heat transfer of GHEs, the adiabatic cylindrical domain model(ACDM) was proposed to describe GHEs heat transfer process. With the proposed model, the analytical solutions of soil temperature distribution and boreholes wall temperature were obtained. The widely accepted finite line source model and engineering test data were used to verify ACDM. Two models were used to calculate and compare boreholes wall temperature variation during 20 a operation under different load conditions and different numbers of boreholes. The results show that the calculation results of temperature of the two models are highly consistent and the consistency increases with the increase of borehole number for large GHEs. ACDM is especially suitable for simulation and large GHEs with boreholes array larger than 30×30. The calculation speed of ACDM is very fast and independent of the number of boreholes, which greatly cuts down the calculation time and is suitable for heat transfer analysis and simulation of large GHEs with large number of boreholes.

Key words: ground source heat pump; geothermal heat exchanger; heat transfer model; analytical solution

自2010年以来，我国浅层地热能的开发利用年均增长速度约为28%，截止2017年底，中国地源热泵装机容量达2万MW，位居世界第一^[1]。随着地源热泵技术在国内的快速发展，地源热泵系统应用趋于大型化方向发展^[2-4]，地埋管换热器规模越来越大，钻孔数量上千甚至上万的情况屡见不鲜。埋管数量达到数百的地埋管换热器一般视为大型地埋管换热器^[5-6]，此类换热器长期运行模拟分析的计算任务量大^[7]，给研究人员特别是设计人员带来很大困难，因此，如何快速、准确预测大型地埋管换热器的长期运行性能是亟需解决的重要问题。

地埋管换热器的传热分析方法大体上可以分为数值方法和解析方法2大类^[8-10]。数值方法适应性强^[11-14]，但是求解埋管数量较多的地埋管换热器的三维非稳态传热时，其计算工作量往往太大^[15-17]。目前广泛采用的地埋管换热器解析方法是以钻孔壁为界分成钻孔内和钻孔外2个部分进行分析，钻孔内通常采用二维或准三维的忽略钻孔内热容影响的计算模型^[18-19]；钻孔外主要是基于有限长线热源^[20-21]和有限长圆柱源^[22-23]方法，采用叠加原理的方法计算管群地埋管换热器传热问题^[24-28]。有限长线热源和有限长圆柱源模型都是基于Kelvin热源理论而提出的热源模型，分别将地埋管与周围岩土换热看成是有限长线热源和有限长柱热源与周围的半无限大均匀介质之间的换热，热源长度等于埋管深度，地面通常视为温度不变的第一类边界条件。通过上述处理，可以得到土壤温度场的解析解，计算得到大幅度简化。虽然解析方法较数值解方法计算工作量大幅度减小，但对于钻孔数量较多的大型地埋管换热器进行长期传热分析计算时，其计算工作量依然很大，计算所需时间过长。

综上，分析埋管数量较多的大型和超大型地埋管换热器传热时，尚缺乏快速有效分析方法。鉴于此，本文基于大型地埋管换热器传热特性提出一种简易解析模型。

1  绝热圆柱域传热模型

对于埋管均匀分布的大型地埋管换热器，其内部埋管数量远超周边埋管数量，故内部埋管传热决定了整个地埋管换热器传热特性。由传热学基本原理可知，在钻孔均匀分布且换热条件相同的情况下，大型埋管换热器内部各埋管与周围土壤的传热可视为各自在一个周边绝热的局部空间域内的传热过程，不受其他地埋管影响。基于此，大型均匀布置地埋管换热器传热问题可简化为周边绝热的单埋管传热问题，从而大幅度降低传热分析任务艰巨性。

1.1　物理模型

均匀布置的地埋管换热器管群通常设计成均匀分布的矩形或三角形阵列，如图1所示，当其他换热条件相同时，内部区域各埋管之间矩形或六边形边界(即图1中的方柱和六棱柱边界)可以看作是绝热边界。为简化分析，将方柱形或六棱柱形区域简化为如图2所示的圆柱体区域，圆柱体区域的横断面与所代表的方柱或六棱柱区域的断面面积相等。

图1　典型地埋管换热器布管形式

Fig. 1　Typical pipe arrangements of geothermal heat exchangers

图2　绝热圆柱域模型示意图

Fig. 2　Diagram of adiabatic cylinder model

为简化分析，采用以下基本假设：

1) 对地埋管与周围土壤传热仅考虑导热，忽略地下水渗流；

2) 地下土壤热物性参数均匀且恒定；

3) 将钻孔壁视为温度均匀的等温面，将地埋管与周围土壤换热视为柱面热源与周围土壤的换热，且热流沿柱面深度方向均匀分布；

4) 忽略沿深度方向的传热，忽略钻孔底部和地表处传热影响；

5) 圆柱区域的外边界为绝热边界；

6) 初始时刻地下温度分布均匀。

1.2　数学模型

根据前面物理模型，地埋管与周围土壤间传热的控制方程为

(1)

式中：θ为土壤过余温度，℃；τ为时间，s；λ为土壤导热系数，W/(m·K)；ρ为土壤密度，kg/m³；c为土壤比热容，J/(kg·K)；r为土壤中任意点到钻孔中心的距离，m。

初始条件为

(2)

式中：r_b为钻孔半径，m；r₁为绝热边界距钻孔中心距离，m。

边界条件为

(3)

(4)

式中：q为单位长度上的发热率，W/m。

1.3　模型求解

基于叠加原理，可以把以上模型分解为3个简单问题的叠加^[18]。假设过余温度θ(r，τ)由θ₁(τ)，θ₂(r)和θ₃(r，τ)这3个部分组成，即

(5)

式中：θ₁(τ)为整个区域平均温度，K，满足

(6)

θ₂(r)满足

(7)

(8)

(9)

由式(7)～(9)可得：

(10)

θ₃(r，τ)满足

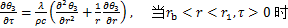  (11)

(12)

(13)

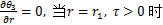(14)

上述方程可以用拉普拉斯变换法或分离变量法求解，其解为

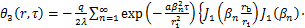
(15)

式中：a为热扩散率，m²/s；β_n为特征方程

(16)

的第n个正根。

这样，式(1)～(4)的解可以写为

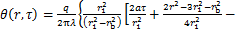
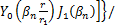
  (17)

1.4　钻孔壁温

解析方法中，钻孔壁温是连接钻孔内外传热分析计算的关键参数。当时间较长时，式(17)右边指数项趋于0，另钻孔壁处r=r_b，则钻孔壁温可由式(17)得到：

(18)

式中：T_b为钻孔壁温，℃；θ_b(τ)为钻孔壁过余温度，℃；t₀为土壤初始温度，℃。

对于地埋管换热器，通常有r_b<1，则式(18)可进一步简化为

(19)

2  模型验证

将目前国内外广泛采用的有限长线热源模型和工程实测数据用于验证建立的绝热圆柱域模型的准确性。

2.1　与有限长线热源模型对比验证

首先，以冷热负荷平衡和不平衡2类工况为例，对比分析绝热圆柱域模型(模型A)与有限长线热源模型^[29](模型B)计算结果。由于土壤温度场中钻孔壁温变化幅度最大，2种模型得到的参数相差也会最大。下面将对比分析模型A计算得到的钻孔壁温与模型B得到的中心钻孔壁温和所有钻孔平均壁温。

冷热负荷平衡工况参数如下：地埋管换热器为30个×30个的钻孔布置，埋管间距为5 m，埋管深度为100 m，钻孔半径r_b为80 mm，地下初始温度为15 ℃，土壤导热系数为2 W/(m·K)，土壤容积比热为4×10⁶ J/(m³·K)。夏季空调时间为4个月，地埋管每延米平均热负荷为30 W/m；冬季供暖时间为3个月，每延米平均热负荷为-40 W/m。

冷热负荷不平衡工况参数如下：地埋管夏季每延米平均放热负荷取3种工况，分别为31.5，33.0和34.5 W/m；地埋管冬季每延米平均热负荷均取为-40 W/m。其他参数同平衡工况。

地下冷热负荷不平衡率ξ的定义如下：

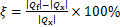(20)

式中：Q_f为年总放热负荷，kJ；Q_x为年总吸热负荷，kJ。上述3种冷热负荷不平衡工况的负荷不平衡率ξ分别为5%，10%和15%。

图3　模型A计算的钻孔壁温与模型B计算的中心钻孔壁温随时间的变化

Fig. 3　Changes of borehole wall temperature with time calculated by Model A and central borehole wall temperature calculated by Model B

图3所示为模型A计算的钻孔壁温与模型B计算的中心钻孔壁温随时间的变化。由图3可见：无论负荷平衡与否，2个模型计算的结果都基本一致(由于2个模型计算结果非常接近，故图3中2个模型得到的温度曲线几乎完全重合)，在20年运行期内，2个模型计算温度差为-0.31~0.18 ℃。这表明采用绝热圆柱域模型预测大型地埋管换热器管群的长期运行性能是可靠的。

图4所示为2种模型计算的所有钻孔平均壁温随时间的变化。由图4可见：模型A计算的钻孔壁温与模型B计算的所有钻孔平均壁温也有较高吻合度，当ξ分别为0，5%，10%和15%，二者计算温差值范围分别为-0.62~0.02，-0.28~0.14，-0.25~0.67和-0.23~1.22 ℃，计算差值不大，即可采用绝热圆柱域模型的计算钻孔壁温代表埋管群的平均钻孔壁温。上述结果还表明，负荷不平衡时，冬季和夏季负荷不平衡率越小，模型A计算结果越准确。

图4　不同ξ时，2种模型计算的所有钻孔平均壁温随时间的变化

Fig. 4　Mean temperature of all boreholes walls changes with time calculated by two models at different ξ

2.2　与工程实测数据对比验证

采用济南某住宅地源热泵空调系统实测数据验证本文建立模型，该地源热泵空调系统地埋管换热器钻孔825个，测试时间为2019年2月15日—2019年2月28日，共336 h。钻孔及回填材料相关参数如下：土壤导热系数为2.13 W/(m·K)，回填材料导热系数为1.05 W/(m·K)，钻孔半径为75 mm，PE管外径为32 mm，U形管2根管子的1/2间距为40 mm。

基于钻孔壁温和热负荷，采用钻孔稳态二维导热模型计算循环液温度^[30]，如图5所示。由图5可见：测试的循环液温度与采用绝热圆柱域模型模拟计算的循环液温度变化趋势基本吻合，在测试的336 h内，二者温差范围为-0.55~0.84 ℃，这表明绝热圆柱域模型用于大型地埋管地源热泵系统的工程计算具有较高的准确性和应用效果。

图5　绝热圆柱域模型模拟温度与测试温度的对比

Fig. 5　Simulation temperatures of adiabatic cylindrical domain model compared with test temperatures

3  模型适用性

对于均匀布管的地埋管换热器，钻孔数量越多，地埋管换热器内部各钻孔区域越接近边界绝热的假设，采用绝热圆柱域模型的计算结果越准确。反之，计算误差越大。下面以负荷不平衡率为15%工况为例，对比不同埋管规模时模型A与模型B计算的所有钻孔平均壁温，分析模型A的适用性，计算结果如图6所示。

由图6可见：地埋管换热器钻孔数量越大，2种模型的计算温度越接近，当钻孔规模分别为10个×10个，20个×20个，30个×30个，40个×40个和50个×50个时，在20年运行期内，2个模型计算温度差值范围分别为-0.34~3.12，-0.26~1.72，-0.23~1.22，-0.21~0.96和-0.20~0.81 ℃。因此，即使冬季和夏季负荷不平衡率达到15%，埋管为30个×30个时，采用模型A的最大温度误差也不超过1.3 ℃，钻孔规模增大，计算误差更小。因此，可认为绝热圆柱域模型适用于埋管规模大于30个×30个时的大型地埋管管群传热分析计算。

图6　不同钻孔规模，2种模型计算的所有钻孔平均壁温随时间的变化(ξ=15%)

Fig. 6　Mean temperature of all boreholes walls changes with time calculated by two models at different borehole sizes (ξ=15%)

进行大型地埋管换热器传热分析时，由于埋管数量多而面临计算工作量过大的问题，可采用绝热圆柱域模型进行传热分析。该模型在满足较高准确性的前提下，计算工作量较小且与埋管数量无关，而且埋管数量越多，误差越小。

4  模型计算时间比较

绝热圆柱域模型通过改变求解地下温度场传热方程的边界条件，将复杂的多埋管传热问题简化为单管传热问题，极大简化了多埋管传热的计算过程。通过有限长线热源模型和绝热圆柱域模型的对比计算发现：在配置为Intel(R) Core(TM) i7-8565U CPU@1.8GHZ 1.99GHZ的电脑上完成绝热圆柱模型模拟计算埋管第20年钻孔壁温的逐日变化，所需时间与钻孔规模无关，仅需24 s，而完成有限长线热源模型按日计算输出30个×30个，40个×40个和50个×50个的钻孔群第20年钻孔平均壁温的逐日变化，所耗时间分别为53.35，100.77和266.18 h，所耗时间分别为绝热圆柱域模型的8 002，15 115和39 927倍，钻孔数量越多，使用绝热圆柱域模型计算速度提升得越快。因此，采用绝热圆柱域模型可实现埋管均布的大型和超大型地源热泵系统长期运行模拟的快速计算，这为大型和超大型地源热泵系统的传热特性分析、工程设计提供了便捷的计算方法。

5  结论

1) 对于大型地埋管换热器，采用绝热圆柱域模型计算的钻孔壁温与有限长线热源模型计算的中心钻孔壁温和所有钻孔平均壁温比较一致，其2种模型计算结果在20年运行期内相差很小；采用绝热圆柱域模型模拟计算的循环液温度与工程测试的循环液温度变化趋势基本吻合。这表明绝热圆柱域模型可用于大型地埋管换热器传热分析计算。

2) 钻孔数量越多，绝热圆柱域模型与有限长线热源模型的计算温度越接近。当钻孔规模大于30个×30个时，2种模型温度计算误差较小。因此，绝热圆柱域模型适用于埋管规模不小于30个×30个的大型和超大型地埋管换热器传热分析。

3) 提出的绝热圆柱域模型计算及其解析解的计算速度超快，可用于均匀布管的大型和超大型地源热泵系统地埋管与土壤传热计算分析。

参考文献：

[1] 自然资源部中国地质调查局, 国家能源局新能源和可再生能源司, 中国科学院科技战略咨询研究院, 等. 中国地热能发展报告: 2018[M]. 北京: 中国石化出版社, 2018: 6-7.

China Geological Survey of Ministry of Natural Resources, Department of New and Renewable Energy of National Energy Administration, Institute of Science and Development of Chinese Academy of Sciences, et al. China geothermal energy development report: 2018[M]. Beijing: China Petrochemical Press, 2018: 6-7.

[2] SU Chang, MADANI H, PALM B. Heating solutions for residential buildings in China: Current status and future outlook[J]. Energy Conversion and Management, 2018, 177: 493-510.

[3] LUO Jin, ZHAO Haifeng, JIA Jia, et al. Study on operation management of borehole heat exchangers for a large-scale hybrid ground source heat pump system in China[J]. Energy, 2017, 123: 340-352.

[4] KUREVIJA T, VULIN D, KRAPEC V. Effect of borehole array geometry and thermal interferences on geothermal heat pump system[J]. Energy Conversion and Management, 2012, 60: 134-142.

[5] 李骥, 乔镖, 马宁, 等. 某医院大型地源热泵系统的设计优化与运行效果验证[J]. 暖通空调, 2020, 50(8): 27-34.

LI Ji, QIAO Biao, MA Ning, et al. Design optimization and operation effect verification of large-scale ground-source heat pump system for a hospital[J]. Heating Ventilating & Air Conditioning, 2020, 50(8): 27-34.

[6] 席加, 秦祥熙, 李少华, 等. 杭州地区大型地源热泵系统全年运行性能研究[J]. 制冷技术, 2017, 37(1): 48-54.

XI Jia, QIN Xiangxi, LI Shaohua, et al. Research on annual operation performance of large scale ground source heat pumps in Hangzhou[J]. Chinese Journal of Refrigeration Technology, 2017, 37(1): 48-54.

[7] CHEN Shuang, WITTE F, KOLDITZ O, et al. Shifted thermal extraction rates in large Borehole Heat Exchanger array-a numerical experiment[J]. Applied Thermal Engineering, 2020, 167: 114750.

[8] GHOREISHI-MADISEH S A, KUYUK A F, RODRIGUES DE BRITO M A. An analytical model for transient heat transfer in ground-coupled heat exchangers of closed-loop geothermal systems[J]. Applied Thermal Engineering, 2019, 150: 696-705.

[9] HU Pingfang, YU Zhongyi, ZHU Na, et al. Performance study of a ground heat exchanger based on the multipole theory heat transfer model[J]. Energy and Buildings, 2013, 65: 231-241.

[10] CHOI J C, LEE S R, LEE D S. Numerical simulation of vertical ground heat exchangers: Intermittent operation in unsaturated soil conditions[J]. Computers and Geotechnics, 2011, 38(8): 949-958.

[11] DUBE KERME E, FUNG A S. Transient heat transfer simulation, analysis and thermal performance study of double U-tube borehole heat exchanger based on numerical heat transfer model[J]. Applied Thermal Engineering, 2020, 173: 115189.

[12] LAMARCHE L, PASQUIER P. Higher-order temporal scheme for ground heat exchanger analytical models[J]. Geothermics, 2019, 78: 111-117.

[13] LI Biao, HAN Zongwei, MENG Xinwei, et al. Study on the influence of the design method of the ground source heat pump system with considering groundwater seepage[J]. Applied Thermal Engineering, 2019, 160: 114016.

[14] FANG Liang, DIAO Nairen, SHAO Zhukun, et al. A computationally efficient numerical model for heat transfer simulation of deep borehole heat exchangers[J]. Energy and Buildings, 2018, 167: 79-88.

[15] LI Min, LAI A C K. Review of analytical models for heat transfer by vertical ground heat exchangers(GHEs): A perspective of time and space scales[J]. Applied Energy, 2015, 151: 178-191.

[16] 孔彦龙, 陈超凡, 邵亥冰, 等. 深井换热技术原理及其换热量评估[J]. 地球物理学报, 2017, 60(12): 4741-4752.

KONG Yanlong, CHEN Chaofan, SHAO Haibing, et al. Principle and capacity quantification of deep-borehole heat exchangers[J]. Chinese Journal of Geophysics, 2017, 60(12): 4741-4752.

[17] CAI Wanlong, WANG Fenghao, CHEN Shuang, et al. Analysis of heat extraction performance and long-term sustainability for multiple deep borehole heat exchanger array: A project-based study[J]. Applied Energy, 2021, 289: 116590.

[18] HELLSTROM G. Ground heat storage: Thermal analyses of duct storage systems[D]. Lund University, 1991: 100-115.

[19] ZENG Heyi, DIAO Nairen, FANG Zhaohong. Heat transfer analysis of boreholes in vertical ground heat exchangers[J]. International Journal of Heat and Mass Transfer, 2003, 46(23): 4467-4481.

[20] GUO Y, HU X, BANKS J, et al. Considering buried depth in the moving finite line source model for vertical borehole heat exchangers: A new solution[J]. Energy and Buildings, 2020, 214: 109859.

[21] ZHANG Xuedan, ZHANG Tiantian, JIANG Yiqiang, et al. Improvement on an analytical finite line source model considering complex initial and boundary conditions: Part 1, model development and validation[J]. Energy and Buildings, 2019, 198: 1-10.

[22] LUO Yongqiang, YU Jinghua, YAN Tian, et al. Improved analytical modeling and system performance evaluation of deep coaxial borehole heat exchanger with segmented finite cylinder-source method[J]. Energy and Buildings, 2020, 212: 109829.

[23] BANDOS T V, CAMPOS-CELADOR A, LOPEZ-GONZALEZ L M, et al. Finite cylinder-source model for energy pile heat exchangers: Effects of thermal storage and vertical temperature variations[J]. Energy, 2014, 78: 639-648.

[24] LUO Yongqiang, GUO Hongshan, MEGGERS F, et al. Deep coaxial borehole heat exchanger: Analytical modeling and thermal analysis[J]. Energy, 2019, 185: 1298-1313.

[25] BERNIER M A, PINEL P, LABIB R, et al. A multiple load aggregation algorithm for annual hourly simulations of GCHP systems[J]. HVAC & R Research, 2004, 10(4): 471-487.

[26] FOSSA M, PRIARONE A, SILENZI F. Superposition of the single point source solution to generate temperature response factors for geothermal piles[J]. Renewable Energy, 2020, 145: 805-813.

[27] KOOHI-FAYEGH S, ROSEN M A. Examination of thermal interaction of multiple vertical ground heat exchangers[J]. Applied Energy, 2012, 97: 962-969.

[28] QIAN Hua, WANG Yungang. Modeling the interactions between the performance of ground source heat pumps and soil temperature variations[J]. Energy for Sustainable Development, 2014, 23: 115-121.

[29] 贺泽群, 于明志, 毛煜东, 等. 基于负荷自适应分配的地埋管换热器传热分析[J]. 工程热物理学报, 2020, 41(8): 2044-2051.

HE Zequn, YU Mingzhi, MAO Yudong, et al. Heat transfer analysis of ground heat exchanger based on self-adaption load distribution method[J]. Journal of Engineering Thermophysics, 2020, 41(8): 2044-2051.

[30] 刁乃仁, 方肇洪. 地埋管地源热泵技术[M]. 北京: 高等教育出版社, 2006: 22-26.

DIAO Nairen, FANG Zhaohong. Ground-coupled heat pump technology[M]. Beijing: Higher Education Press, 2006: 22-26.

(编辑  秦明阳)

收稿日期： 2020 -12 -17； 修回日期： 2021 -02 -10

基金项目(Foundation item)：国家自然科学基金资助项目(41702325)；山东省自然科学基金资助项目(ZR2017MEE037)；济南市科研带头人工作室项目(2019GXRC066) (Project(41702325) supported by the National Natural Science Foundation of China; Project(ZR2017MEE037) supported by the Natural Science Foundation of Shandong Province; Project(2019GXRC066)supported by the Jinan Scientific Research Leader Studio)

通信作者：于明志，博士，教授，从事可再生能源利用及建筑节能技术等研究；E-mail：yumingzhiwh@163.com

DOI: 10.11817/j.issn.1672-7207.2021.06.021

引用格式：张方方, 路伟, 朱科, 等. 用于大型地埋管换热器传热分析的绝热圆柱域模型[J]. 中南大学学报(自然科学版), 2021, 52(6): 1915-1923.

Citation:ZHANG Fangfang, LU Wei, ZHU Ke, et al. Adiabatic cylindrical domain model for heat transfer analysis of large geothermal heat exchanger[J]. Journal of Central South University(Science and Technology), 2021, 52(6): 1915-1923.