DOI: 10.11817/j.issn.1672-7207.2019.04.010

深海扬矿泵内部非定常流体径向力研究

赵贺¹，刘少军^{1, 2}，胡小舟¹

(1. 中南大学 机电工程学院，湖南 长沙，410083；

2. 中南大学 深圳研究院，广东 深圳，518000)

摘要：基于深海扬矿泵是深海采矿系统的关键设备，泵内部流动较复杂，无法用公式对流体径向力进行理论计算等，采用试验和数值模拟方法对其作用规律以及产生机理进行研究。首先，对泵内流场进行定常数值计算。然后，进行非定常数值计算，得到泵内压力和径向力的时域和频域图。研究结果表明：在对泵内流场进行定常数值计算时，发现扬程、功率和效率的模拟值与试验值较吻合，从而验证了数值模拟方法的可行性；叶轮和导叶的动静干涉是泵内产生压力脉动和不平衡径向力的重要原因；泵内压力和径向力均呈周期性脉动；叶轮内的压力脉动周期和主频与导叶的叶片数相关，导叶内的压力脉动周期和主频与叶轮叶片数相关，而两者的径向力脉动周期和主频则均与叶轮叶片数相关。

关键词：深海扬矿泵；非定常流体径向力；压力脉动；数值模拟

中图分类号：TH311             文献标志码：A         文章编号：1672-7207(2019)04-0829-08

Study on unsteady fluid radial force in deep-sea lifting pump

ZHAO He¹, LIU Shaojun^{1, 2}, HU Xiaozhou¹

(1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;

2. Shenzhen Research Institute, Central South University, Shenzhen 518000, China)

Abstract: Considering that deep-sea lifting pump is the key equipment of deep-sea mining system, the internal flow is complex, and the radial force of the fluid can not be calculated theoretically by formulas, the experimental and numerical simulation methods were used to study the regular and the production mechanism. Firstly, the steady flow field in the pump was calculated. Then, the unsteady flow field in the pump was calculated, and the time-domain and frequency-domain diagrams of pressure and radial force in the pump were obtained. The results show that the simulated values of the external characteristic curve agree well with the experimental values, which verifies the feasibility of the numerical simulation method. The dynamic and static interference between the impeller and the guide vane is an important cause of pressure pulsation and unbalanced radial force in the pump. The pressure and radial force in the pump have periodic pulsation characteristics. The pressure pulsation period and the main frequency in the impeller are related to the number of vanes during the pressure pulsation period and the main frequency in the vane are related to the number of impeller blades. The radial force pulsation period and the main frequency of them are only related to the number of impeller blades.

Key words: deep-sea lifting pump; unsteady fluid radial force; pressure pulsation; numerical simulation

近年来，随着陆上矿产资源逐渐减少，海底矿产资源的开发与利用已成为国际社会关注的热点。由于深海矿产资源往往处于超常极端环境并且具有特殊的赋存状态，这就要求深海扬矿泵要能适应极端恶劣与复杂的深海作业环境，因此，与一般的陆地普通多级电泵相比，深海扬矿泵应具有高扬程、粗颗粒、轴向流和可回流的特点。同时，作为采矿系统的动力输送部件，深海扬矿泵对性能和稳定性也往往有着较高的要求。这说明深海和陆地普通多级泵在机理和特性方面有较大不同，两者在研究内容和难度上也有较大区别。深海扬矿泵属于高比转速离心泵型，有离心式叶轮和空间式导叶，在运转过程中，其内部流场的不稳定流动会导致叶轮和导叶表面的周向压力分布不均，进而产生不平衡的流体径向力，严重时还会引起泵的振动和噪声，影响其运行稳定性。关于离心泵内部的非定常流动，目前国内外学者多采用数值模拟和试验的方法进行研究。一些研究者以蜗壳泵为研究对象，采用数值模拟方法对其内部的压力和流体径向力的脉动特性进行了探讨^[1-5]。张宁等^[6]采用试验方法对蜗壳周向监测点的压力脉动频谱进行了分析。GUO 等^[7]采用试验的方法对叶轮和导叶内的压力脉动、叶轮上的径向力以及泵轴的振动情况进行了研究。江伟等^[8-9]结合数值模拟和试验方法，对蜗壳式离心泵内的流场分布和压力脉动规律进行了研究，发现这2种方法得到的结果基本一致。刘厚林等^[10-11]对径向导叶式的多级离心泵进行了非定常数值模拟并分析了叶轮和导叶内的压力脉动规律。以上研究主要关注陆用蜗壳和径向导叶式离心泵的非定常流动特性，而目前有关空间导叶式深海扬矿泵内部的非定常流体径向力的研究很少。为此，本文作者以国内研制的两级深海扬矿泵为研究对象，基于试验和数值模拟的方法对泵内的非定常流动特性进行研究，重点分析泵内部的压力和非定常流体径向力的作用规律和诱发机理，以便为深海扬矿泵的稳定运行和优化提供参考。

1  数值计算

1.1  数值模型

深海扬矿泵需要具备高扬程的特点，一般为多级，本文在保证数值模拟准确性的前提下综合考虑计算机的性能和时长，以国内研制的两级深海扬矿泵为研究对象^[12-14]。为了保证粗颗粒的通过性，采用以加宽流道为目的的放大流量设计^[15]，致使其工作流量与设计流量点分离。主要参数为：设计流量Q₁=800 m³/h，额定工作流量Q₂=420 m³/h，单级清水扬程H=40 m，额定转速n=1 450 r/min，叶轮的叶片数Z₁=3，导叶的叶片数Z₂=4。根据两级深海扬矿泵的设计参数，利用专业的旋转机械建模软件CFturbo进行建模，得到的模型如图1所示。

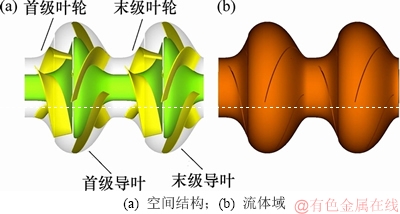
图1  两级泵空间结构与流体域

Fig. 1  Two-stage pump structure and fluid domain

1.2  计算方法

采用专业的泵类CFD仿真软件pumplinx对两级深海扬矿泵进行定常和非定常流动的数值模拟。在对泵内流场进行数值计算时，采用有限体积法对N-S方程进行离散，同时，采用simples算法对压力和速度进行耦合计算，收敛精度设置为10^-4。

在定常模拟时，采用多参考坐标系模型(MRF)和标准K-Epsilon湍流模型进行全流道数值计算。在非定常模拟时，选取已收敛的定常计算结果作为初始条件，采用双向耦合的particle粒子追踪模型、动网格模型和RNG K-Epsilon湍流模型进行求解。叶轮每转过12°设为1个时间步长，根据叶轮转速可计算时间步长为0.0 013 793 s。为了保证非定常计算具有较好的收敛性，共计算9个旋转周期并取最后1个周期内已收敛的结果进行分析。

1.3  网格划分与边界条件设置

计算域为两级叶轮和导叶所组成的全流道流体域，将其导入pumplinx软件进行网格划分。pumplinx内置的笛卡尔网格生成器采用几何等角自适应二元树算法，可以对流体域进行自适应笛卡尔六面体网格划分，并对叶片区域进行自动加密处理。其中，两级泵的全流道网格数为1 733 857个，单级叶轮的网格数为361 585个，单级导叶的网格数为489 448个，如图2所示。在首级叶轮的进口设置压力入口边界条件，设定进口总压为1×10⁵ Pa；在末级导叶的出口设置流量出口边界条件；在流体域的接触壁面上设置光滑边界条件，并在近壁区采用标准壁面函数。

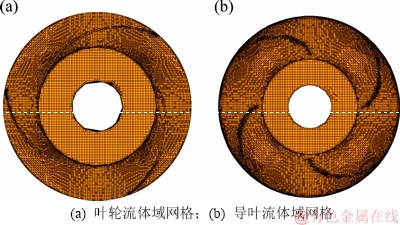
图2  泵流体域网格

Fig. 2  Pump fluid domain grid

2  计算结果与分析

2.1  数值仿真与试验对比

为了验证本文所提出的数值模型和计算方法的准确性，将两级提升泵在清水工况下定常计算得到的外特性仿真曲线与该泵在深海矿产资源开发利用技术国家重点实验室进行清水试验得到的外特性试验曲线^[16-17]进行对比，如图3所示。

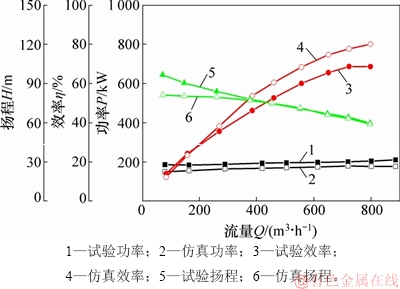
图3  两级泵的仿真与试验曲线

Fig. 3  Simulation and test curves of two-stage pump

从图3可以看出：随着流量增加，仿真与试验所得到的外特性曲线在趋势上具有较好的一致性，两者的效率与功率曲线均呈递增趋势，而扬程曲线均呈递减趋势；此外，两者在额定工作流量附近的扬程、功率和效率均较好对应，相对误差均在10%以内；而由于小流量工况下容易产生二次流和涡流等不稳定流动，此时仿真与试验的结果相差稍大，最大相对误差为15%，但仍在可接受范围之内。总体上，本文的数值模型和计算方法能较准确地预测两级深海扬矿泵的外特性，可以用于对泵内的非定常流体径向力进行研究。

2.2  泵内部的非定常流动分析

在分析泵内部的非定常流动特性时，对于陆用的普通多级泵来说，多在清水工况下进行，而对于输送固体颗粒的渣浆泵，也主要是针对卧式布置的安装方式来进行分析。本文研究的对象是深海多级扬矿泵，采用立式安装方式串联于长距离输送管道上，并要求其能够输送较粗的矿石颗粒；此外，陆用普通多级泵一般是在额定工况下运行，而本文研究的深海泵为了保证粗颗粒的通过性，按照工作流量和设计流量分离进行设计，导致其内部非定常流动现象会更加严重。以上分析不仅揭示了深海与普通多级泵在进行非定常流动分析时的差异性，同时也说明深海多级泵内部的非定常流动特性更容易影响其运行稳定性。对深海扬矿泵进行非定常数值模拟时，考虑到两级泵内非定常流动特性的相似性^[18]以及计算时长，仅选用首级泵为研究对象，并在额定转速n=1 450 r/min，额定工作流量Q=420 m³/h，以及颗粒密度ρ=2 000 kg/m³，粒径d=10 mm，体积分数φ=6%的固液两相流工况下进行。

2.2.1  压力脉动的机理及特性分析

在深海泵正常工作过程中，其叶轮旋转，导叶则保持静止，这样两者相互影响，即发生动静干涉，造成内部流体的压力脉动，而这些脉动的压力作用在叶轮和导叶上又会使其产生不平衡的流体径向力，这也是泵内部流体径向力的主要来源。因此，为了研究泵内的非定常流体径向力，应首先对泵内的压力脉动规律进行研究。为了获得泵内不同位置的压力脉动情况，在叶轮和导叶的流道内设置监测点。其中，在叶轮叶片的压力面设置4个跟随叶片运动的监测点P₁~P₄，吸力面也设置4个跟随叶片运动的监测点S₁~S₄，在导叶工作面设置3个静止监测点G₁~G₃。监测点的具体位置分布如图4所示。

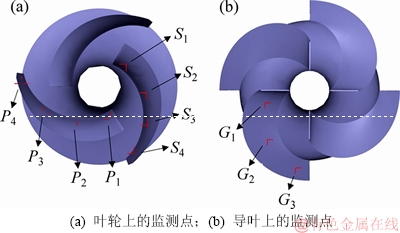
图4  监测点位置分布

Fig. 4  Distribution of monitoring points

1) 叶轮内的压力脉动分析。图5所示为叶轮流道内监测点的压力脉动时域图，其中横坐标为叶轮转过的角度，纵坐标为监测点的静压。

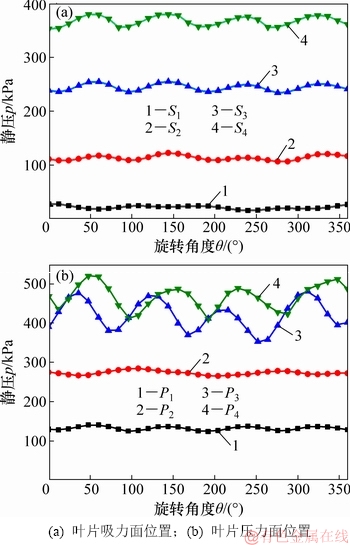
图5  叶轮监测点的压力脉动时域图

Fig. 5  Time domain diagram of pressure pulsation at monitoring points of impeller

从图5可以看出：各监测点的压力脉动规律基本相同，均呈现出周期性的压力脉动特征，但不同监测点的压力脉动均值和幅值不同。由于叶轮上的监测点会随叶片一起转动，在1个旋转周期内叶轮的每个叶片均会与导叶发生4次动静干涉，这些监测点相应地也会受到4次动静干涉的影响；同时，图5中各监测点也均呈现出4个压力脉动周期的变化规律，且越接近叶轮出口处即动静干涉区域，监测点的压力脉动幅值也越大，这说明叶轮内的压力脉动信号来自叶轮出口，与叶轮和导叶的动静干涉有重要联系。此外，距叶轮进口相同位置处叶片压力面上监测点的压力脉动均值和幅值均要比吸力面的大。因为只有当叶片的压力面受力大于吸力面时，流体才会对叶轮作负功，叶轮才能传递流量给流体。而对于同侧监测点而言，从叶轮进口至出口，由于叶轮作功，流体的压力脉动均值逐渐增大。

为了对叶轮内部的压力脉动情况进行进一步分析，采用频域分析法将各监测点的静压值减去平均值后进行快速傅里叶变换，得压力脉动的频域图，如图6所示。

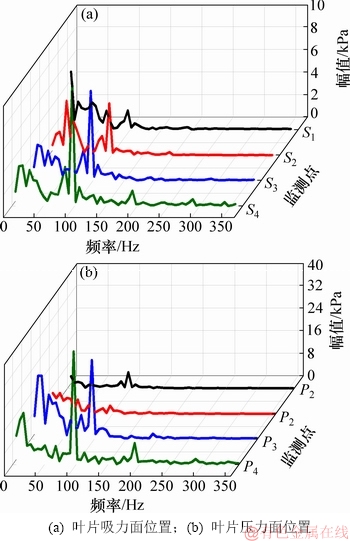
图6  叶轮监测点的压力脉动频域图

Fig. 6  Frequency domain diagram of pressure pulsation at monitoring points of impeller

从图6可以看出：各监测点的压力脉动均处于低频区，且呈现出主频脉动特征；脉动主频出现在96 Hz处，是转频24 Hz的4倍，该倍数与导叶的叶片数相等，同时，这也与图5中监测点所呈现的4个周期的脉动规律相一致，说明叶轮内的压力脉动主要受到转频与导叶叶片数的影响。此外，与时域分析结果相同，频域图中压力面监测点的脉动幅值普遍比吸力面的大；监测点的脉动幅值在叶轮出口位置最大，越远离出口位置其值越小。

2) 导叶内的压力脉动分析。图7所示为导叶流道内监测点的压力脉动图。

从图7(a)可以看出：导叶工作面上3个监测点的压力脉动规律基本相同，均呈现出周期性的压力脉动特征，但各个监测点的压力脉动均值和幅值均不相同；在叶轮转1圈过程中，叶轮的3个叶片会依次扫过监测点所在的导叶叶片，两者间相应发生3次动静干涉，同时，图7(a)中各监测点也均表现出3个脉动周期的变化规律，且越接近导叶入口位置即动静干涉区域，监测点的压力脉动幅值越大，这说明导叶内的压力脉动信号来自导叶入口，与叶轮和导叶的动静干涉有密切联系。此外，从导叶入口至出口，监测点的压力脉动均值逐渐增大，这说明导叶的设计合理，起到了将内部流体的动能转换为压能的作用。

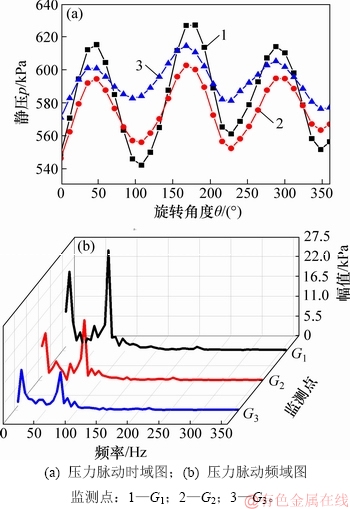
图7  导叶监测点的压力脉动图

Fig. 7  Diagram of pressure pulsation at monitoring points of guide vane

采用频域分析法对导叶的压力脉动情况进行进一步分析，结果见图7(b)。从图7(b)可以看出：3个监测点均呈现出低频压力脉动特征，且脉动主频均出现在72 Hz处，是转频的3倍，与叶轮的叶片通过频率即叶频相等，这说明导叶内的压力脉动主要受叶频的影响。此外，从导叶入口至出口，随着远离动静干涉区域，监测点的压力脉动幅值也呈现出逐渐减小的变化规律。

2.2.2  流体径向力的作用机理及特性分析

前面通过对叶轮和导叶内的压力脉动情况分析证实了叶轮与导叶间的动静干涉是泵内产生压力脉动的重要原因，而泵内的流体径向力又是压力脉动的结果，故为了研究动静干涉作用对泵内流体径向力的直接影响，现通过积分将作用于叶轮和导叶上X和Y方向的流体径向力提取出来进行分析。

1) 流体径向分力的时域分析。首先，对叶轮旋转一圈过程中的流体径向分力进行时域分析，得到X和Y向的流体径向力的时域图，如图8所示(其中，横坐标为叶轮的旋转角度，纵坐标为叶轮与导叶在X和Y向的流体径向力)。

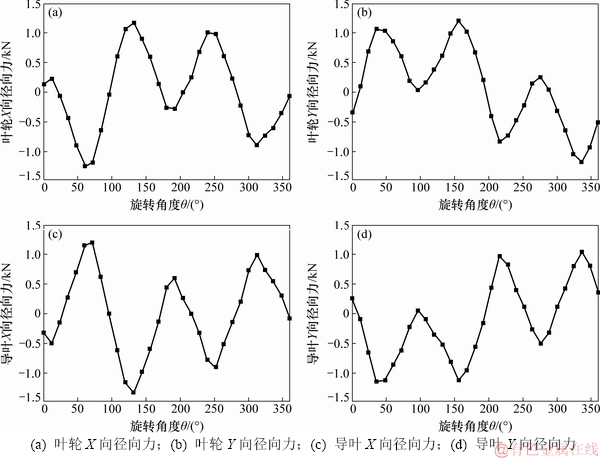
图8  流体径向力时域图

Fig. 8  Time domain diagram of fluid radial force

从图8可以看出：由于动静干涉的影响，在1个旋转周期内，叶轮与导叶在X和Y向所受的径向力随叶轮的旋转均呈一定的周期性，其波形均存在3次波峰及波谷，与叶轮的叶片数相同，这说明泵内流体径向力的峰谷形成规律主要受叶轮叶片数的影响。由于泵的实际工作流量偏离设计流量，其内部流场呈不稳定流动特征，叶轮和导叶表面周向压力分布不均匀，两者的径向分力虽呈现出周期性的方向变化，但在正、负2个方向上的极大值呈不等变化；此外，在叶轮转过个角度时，叶轮和导叶在X或Y向的径向力呈大小近似相等、方向相反规律变化。

2) 流体径向分力的频域分析。为了对流体径向分力进行进一步分析，通过快速傅里叶变换，对径向分力进行频域分析。

图9所示为叶轮和导叶在X和Y向径向力的脉动频域图。与泵内监测点的压力脉动现象一样，流体径向力也呈现出低频压力脉动特征，脉动主频对应的是叶频72 Hz处，此频率下的径向力脉动幅值要远比其他频率位置的大，此外，在2倍和3倍叶频处也有着一定的脉动峰值，这说明泵内流体径向力的幅值变化主要受1倍叶频的影响。

3) 流体径向合力的变化规律与分析。前面通过对叶轮和导叶在单方向径向力的时域和频域分析已解释了泵内流体径向力的脉动现象和规律，但为了深入分析叶轮与导叶的流体径向合力的非定常变化规律，现将X和Y这2个方向上的径向力结合起来，对1个旋转周期内的径向合力作矢量图进行分析。流体径向力矢量图如图10所示。

图10所示为叶轮和导叶在1个旋转周期内的径向力矢量图，其中，横坐标为X方向的径向力，纵坐标为Y方向的径向力，曲线上任一点到坐标系原点的连线则代表某时刻径向合力的大小和方向。从图10可以看出：在1个旋转周期内，叶轮和导叶的径向力均以原点为中心，随叶轮的旋转呈一定的周期性，即呈3圈分布，每圈有4个峰值点。这是由于叶轮有3个叶片，导叶有4个叶片，在叶轮转1圈过程中，每转30°就会和导叶发生1次干涉。其中导叶上的4个叶片会按先后顺序依次和叶轮发生干涉；当导叶的4个叶片均与叶轮发生1次干涉后，两者所受的径向力就会发生1个周期的变化，也就对应着图10中的1圈径向力变化。在这过程中，叶轮和导叶会发生4次动静干涉，导致两者的径向力均有4次周向波动，从而产生4个峰值点。而在1个旋转周期内，导叶的4个叶片均会与叶轮发生3次干涉，两者的径向力也都会发生3个周期的变化，从而对应图10中的3个径向力周期，相应地也会产生12个峰值点。这就是图8中叶轮和导叶的径向分力出现3个波形变化的原因。

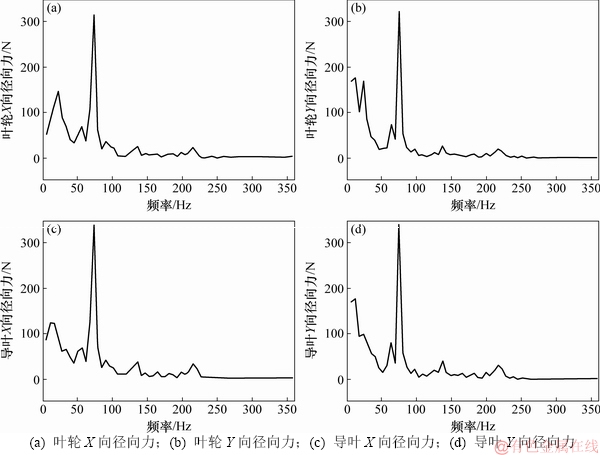
图9  流体径向力频域图

Fig. 9  Frequency domain diagram of fluid radial force

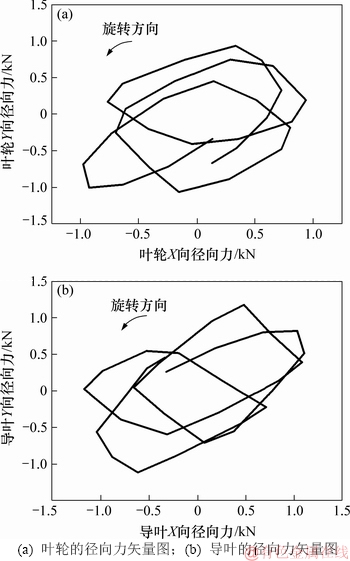
图10  流体径向力矢量图

Fig. 10  Vector diagram of fluid radial force

综上可知：在1个旋转周期内，叶轮和导叶径向力变化的周期数均等于叶轮的叶片数；每个径向力变化周期内的峰值点数则与导叶的叶片数相等；每个峰值点也对应着叶轮和导叶的1次动静干涉。这将叶轮与导叶的结构以及两者间的动静干涉与其所受的流体径向力联系起来，解释了泵内非定常流体径向力的作用规律和诱发机理。

3  结论

1) 由于叶轮和导叶的动静干涉作用，泵内存在较明显的压力脉动和不平衡流体径向力，因此，深海扬矿泵的运行不稳定性问题应该得到重视。

2) 泵内的压力脉动幅值从叶轮进口至出口逐渐增大，导叶内则情况相反，说明叶轮出口和导叶进口之间的区域所受动静干涉的影响最大；叶轮和导叶所受的流体径向力呈大小相等、方向相反的规律变化。

3) 在1个旋转周期内，泵内压力呈周期性脉动，叶轮内的压力脉动周期数等于导叶的叶片数，导叶内的压力脉动周期数等于叶轮的叶片数；叶轮和导叶的流体径向力也均呈一定的周期性变化，变化周期数均与叶轮的叶片数相等。

4) 在频域分析中，叶轮内压力脉动的影响因素主要为转频与导叶叶片数的乘积；导叶内压力脉动的影响因素主要为叶轮的叶片通过频率即叶频；而两者流体径向力幅值变化的影响因素则均主要为叶频。

参考文献：

[1] 杨敏官, 王兴宁, 高波, 等. 离心泵内部非定常水力激励特性[J]. 排灌机械工程学报, 2014, 32(12): 1023-1028.

YANG Minguan, WANG Xingning, GAO Bo, et al. Unsteady hydrodynamic excitation characteristics in centrifugal pump[J]. Journal of Drainage and Irrigation Machinery Engineering, 2014, 32(12): 1023-1028.

[2] 袁建平, 付燕霞, 刘阳, 等. 基于大涡模拟的离心泵蜗壳内压力脉动特性分析[J]. 排灌机械工程学报, 2010, 28(4): 310-314.

YUAN Jianping, FU Yanxia, LIU Yang, et al. Analysis on pressure fluctuation within volute of centrifugal pump based on large eddy simulation[J]. Journal of Drainage and Irrigation Machinery Engineering, 2010, 28(4): 310-314.

[3] BARRIO R, FERNNDEZ J, BLANCO E, et al. Estimation of radial load in centrifugal pumps using computational fluid dynamics[J]. European Journal of Mechanics B: Fluids, 2011, 30(3): 316-324.

[4] ZHANG Ning, YANG Minguan, GAO Bo, et al. Unsteady pressure pulsation and rotating stall characteristics in a centrifugal pump with slope volute[J]. Advances in Mechanical Engineering, 2014, 2015, 34(6): 189-194.

[5] 张忆宁, 曹卫东, 姚凌钧, 等. 不同叶片出口角下离心泵压力脉动及径向力分析[J]. 流体机械, 2017, 45(11): 34-40.

ZHANG Yining, CAO Weidong, YAO Lingjun, et al. Analysis on pressure fluctuation and radial thrust of centrifugal pump under different blade outlet angle[J]. Fluid Machinery, 2017, 45(11): 34-40.

[6] 张宁, 杨敏官, 高波, 等. 低比转速离心泵压力脉动频谱特性的试验研究[J]. 工程热物理学报, 2017, 38(9): 1872-1876.

ZHANG Ning, YANG Minguan, GAO Bo, et al. Experimental study on pressure fluctuation spectrum characteristics of a low specific speed centrifugal pump[J]. Journal of Engineering Thermophysics, 2017, 38(9): 1872-1876.

[7] GUO S, OKAMOTO H. An experimental study on the fluid forces induced by rotor-stator interaction in a centrifugal pump[J]. International Journal of Rotating Machinery, 2007, 9(2): 135-144.

[8] 江伟, 李挺, 王玉川, 等. 导叶式离心泵内部流场数值模拟与试验[J]. 农业机械学报, 2017, 48(9): 121-128.

JIANG Wei, LI Ting, WANG Yuchuan, et al. Numerical simulation and experiment of flow field in centrifugal pump with vane diffuser[J]. Transactions of The Chinese Society of Agricultural Machinery, 2017, 48(9): 121-128.

[9] GONZALEZ J, PARRONDO J, SANTOLARIA C, et al. Steady and unsteady radial forces for a centrifugal pump with impeller to tongue gap variation[J]. Journal of Fluids Engineering, 2006, 128(3): 454-462.

[10] 刘厚林, 周孝华, 王凯, 等. 多级离心泵径向导叶内压力的脉动特性[J]. 中南大学学报(自然科学版), 2014, 45(9): 3295-3300.

LIU Houlin, ZHOU Xiaohua, WANG Kai, et al. Analysis on pressure fluctuation of radial diffusers in a multistage centrifugal pump[J]. Journal of Central South University(Science and Technology), 2014, 45(9): 3295-3300.

[11] 马新华, 冯琦, 蒋小平, 等. 导叶叶片数对多级离心泵压力脉动的影响[J]. 排灌机械工程学报, 2016, 34(8): 665-671.

MA Xinhua, FENG Qi, JIANG Xiaoping, et al. Influence of guide vane blade number on pressure fluctuation in multistage centrifugal pump[J]. Journal of Drainage and Irrigation Machinery Engineering, 2016, 34(8): 665-671.

[12] SHI Weidong, ZHOU Ling, LU Weigang, et al. Numerical simulation and experimental study of different stages deep-well centrifugal pump[J]. Journal of Computational & Theoretical Nanoscience, 2013, 10(12): 2897-2901.

[13] 周岭, 施卫东, 陆伟刚, 等. 深井离心泵数值模拟与试验[J]. 农业机械学报, 2011, 42(3): 69-73.

ZHOU Ling, SHI Weidong, LU Weigang, et al. Numerical simulation and experiment on deep well centrifugal pump[J]. Transactions of the Chinese Society of Agricultural Machinery, 2011, 42(3): 69-73.

[14] 王川, 陆伟刚, 施卫东, 等. 不锈钢冲压潜水井泵的数值计算与试验验证[J]. 江苏大学学报(自然科学版), 2012, 33(2): 176-180.

WANG Chuan, LU Weigang, SHI Weidong, et al. Numerical calculation and experimental verification of stainless steel stamping submersible well pump[J]. Journal of Jiangsu University(Natural Science Edition), 2012, 33(2): 176-180.

[15] 邹伟生, 李哲奂, 陈爱黎. 海洋采矿扬矿电泵的研究[J]. 中南大学学报(自然科学版), 2011, 42(增刊2): 221-225.

ZOU Weisheng, LI Zhehuan, CHEN Aili. Lifting motor pump in deep sea mining[J]. Journal of Central South University(Science and Technology), 2011, 42(Suppl 2): 221-225.

[16] 李哲奂. 扬矿电泵内流场数值模拟及性能预测[D]. 长沙: 湖南大学机械与运载工程学院, 2013: 36-37.

LI Zhehuan. Lifting motor pump's internal flow field numerical simulation and performance prediction[D]. Changsha: Hunan University. College of Mechanical and Vehicle Engineering, 2013: 36-37.

[17] 唐达生, 阳宁, 龚德文, 等. 深海采矿锰结核泵的试验研究[J].海洋工程, 2015, 33(4): 101-107.

TANG Dasheng, YANG Ning, GONG Dewen, et al. Experimental study of manganese nodules pump in deep-sea mining[J]. The Ocean Engineering, 2015, 33(4): 101-107.

[18] 施卫东, 徐燕, 张启华, 等. 多级潜水泵内部压力脉动特性[J].排灌机械工程学报, 2014, 32(3): 196-201.

SHI Weidong, XU Yan, ZHANG Qihua, et al. Characteristics of pressure pulsation in multi-stage submersible pump[J]. Journal of Drainage and Irrigation Machinery Engineering, 2014, 32(3): 196-201.

(编辑  陈灿华)

收稿日期：2018-06-15；修回日期：2018-08-30

基金项目(Foundation item)：国家重点研发计划项目(2016YFC0304103-4)；深圳市基础研究项目(JCYJ20150929102555935)；深圳市未来产业发展专向资金资助项目(HYZDFC20140801010002)(Project(2016YFC0304103-4) supported by the National Key Research and Development Plan; Project(JCYJ20150929102555935) supported by the Shenzhen Basic Research Program; Project(HYZDFC20140801010002) supported by Shenzhen Future Industry Development Special Fund)

通信作者：胡小舟，博士，副教授，从事深海采矿技术研究；E-mail: csu_huxiaozhou@163.com